中考数学一轮复习知识点+题型专题讲义09 分式与分式方程（学生版） 13页

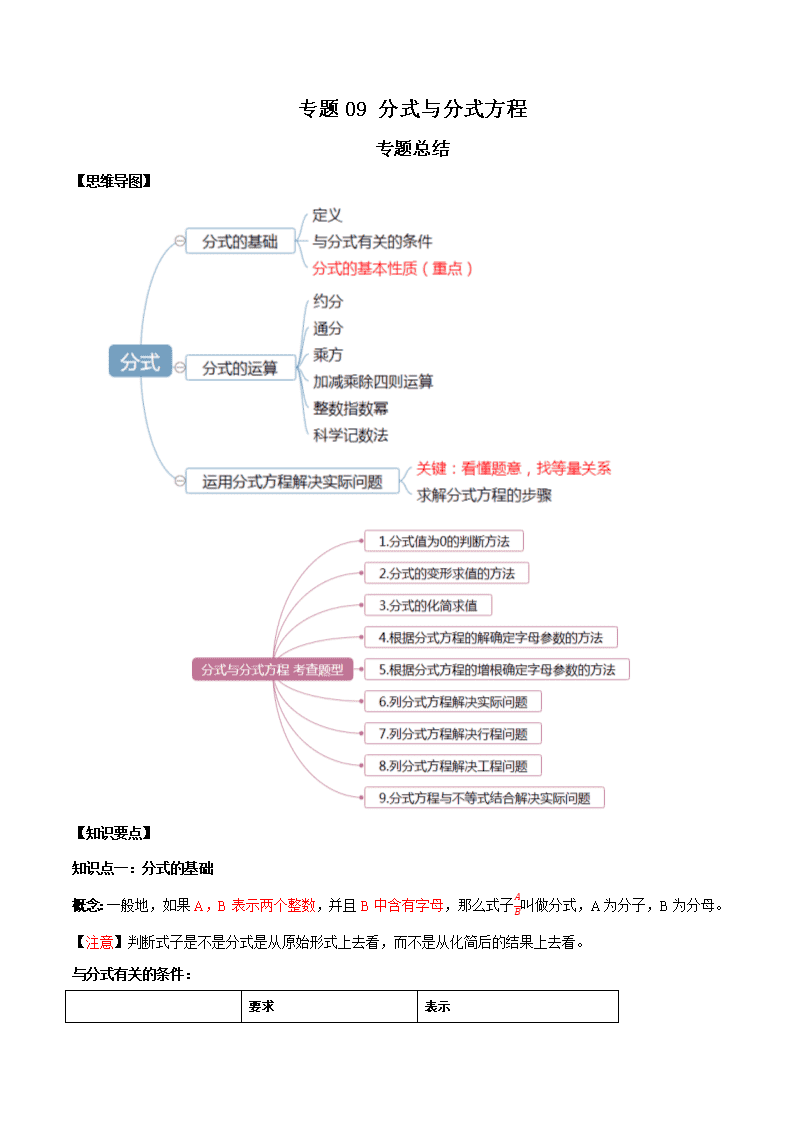
专题 09 分式与分式方程 专题总结 【思维导图】 【知识要点】 知识点一：分式的基础 概念：一般地，如果 A，B 表示两个整数，并且 B 中含有字母，那么式子 叫做分式，A 为分子，B 为分母。 【注意】判断式子是不是分式是从原始形式上去看，而不是从化简后的结果上去看。 与分式有关的条件： 要求 表示 分式有意义 分母≠0 ≠ 0分式无意义 分母=0 ㌳ 0分式值为 0 分子为 0 且分母不为 0 ㌳ 0Ͳ 0分式值为正或大于 0 分子分母同号 1 A>0,B>0 2 A<0,B<0 分式值为负或小于 0 分子分母异号 ①A>0,B<0 ②A<0,B>0 分式值为 1 分子分母值相等 A=B 分式值为-1 分子分母值互为相反数 A+B=0 1．（2019·湖北中考模拟）无论 a 取何值时，下列分式一定有意义的是（ ） A． B． C． D． 2．（2019·江苏中考真题）若代数式 有意义，则实数 的取值范围是（ ） A． ㌳ B． ㌳ C． D． 3．（2018·沭阳县马厂实验学校中考模拟）在 , , , o , o , 中分式的个数有（ ） A．2 个 B．3 个 C．4 个 D．5 个 考查题型一 分式值为 0 的判断方法 1．（2018·安徽中考模拟）分式 的值为 0,则 x 的取值为( ) A．x=-3 B．x=3 C．x=-3 或 x=1 D．x=3 或 x=-1 2．（2018·云南中考模拟）当式子 Ͷ 的值为零时，x 的值是（ ） A． B． C． D． 或 3．（2019·广西中考真题）若分式 的值为 0，则 x 的值为（ ） A．0 B．1 C．﹣1 D．±1 知识点二：分式的运算（重点） 基本性质（基础）：分式的分子和分母同乘（或除以）一个不等于 0 的整式，分式的值不变。 字母表示： ㌳ ， ㌳ ， 其中 A、B、C 是整式，C 0。 拓展：分式的符号法则：分式的分子、分母与分式本身的符号，改变其中任何两个，分式的值不变，即 ㌳ ㌳ ㌳ 注意：在应用分式的基本性质时，要注意 C 0 这个限制条件和隐含条件 B 0。 1．（2019·山东中考模拟）若 x，y 的值均扩大为原来的 3 倍，则下列分式的值保持不变的是（ ） A． o B． o C． o D． o o 2．（2017·山东中考模拟）若把分式 o o 的 x、y 同时扩大 10 倍，则分式的值（ ） A．扩大为原来的 10 倍 B．缩小为原来的 C．不变 D．缩小为原来的 3．（2017·河北中考模拟）若分式 o o 中的 a、b 的值同时扩大到原来的 3 倍，则分式的值（ ） A．不变 B．是原来的 3 倍 C．是原来的 6 倍 D．是原来的 9 倍  分式的约分 约分的定义：根据分式的基本性质，把一个分式的分子与分母的公因式约去。 最简公式的定义：分子与分母没有公因式的分式。 分式约分步骤： 1）提分子、分母公因式 2）约去公因式 3）观察结果，是否是最简分式或整式。 注意： 1.约分前后分式的值要相等. 2.约分的关键是确定分式的分子和分母的公因式. 3.约分是对分子、分母的整体进行的，也就是分子的整体和分母的整体都除以同一个因式 1．（2016·山东中考真题）下列分式中，最简分式是（ ） A． B． C． oo o D． 䁑 2．（2018·山东中考模拟）下列分式中，最简分式是 ( ) A． o oo B． ⸲ 䁑 C． D． 䁑 3．（2019·山东中考真题）计算 的正确结果是( ) A． B． C． D．  分式的通分 通分的定义：根据分式的基本性质，把几个异分母的分式分别化成与原来的分式相等的同分母分式，叫做 分式的通分。 最简公分母的定义：取各分母所有因式的最高次幂的积作公分母，这样的公分母叫做最简公分母。 分式通分的关键：确定最简公分母 确定分式的最简公分母的方法 1.因式分解 2.系数：各分式分母系数的最小公倍数； 3.字母：各分母的所有字母的最高次幂 4.多项式：各分母所有多项式因式的最高次幂 5.积 约分与通分的相同点： 1．（2019·广西中考模拟）关于分式的约分或通分，下列哪个说法正确（ ） A． 约分的结果是 B．分式 2 1 1x  与 的最简公分母是 x﹣1 C． 约分的结果是 1 D．化简 ﹣ 2 1 1x  的结果是 1 2．（2014·广西中考真题）下列三个分式 、 、 的最简公分母是（ ） A．4（m﹣n）x B．2（m﹣n）x2 C． D．4（m﹣n）x2 3．下列各题所求的最简公分母，错误的是 ( ) A． 与 䁑 的最简公分母是 6x2 B． o 与 o 的最简公分母是 6a2b2c C． 与 的最简公分母是 x2-9 D． o 与 o 的最简公分母是 mn(x+y)·(x-y) 4．（2017·江苏宜陵镇中学初二月考）把分式  x x y ， y x y ， o 进行通分，它们的最简公分母是（ ） A． o B． oC． ( )( )x y x y  D． o o o 考查题型二 分式的变形求值的方法 1．（2019·四川省成都市簇锦中学中考模拟）已知 o ㌳ ，则 o 的值是_____． 2．（2019·上海中考模拟）如果 o ㌳ ，那么 o ㌳ ______． 3．（2012·广西中考模拟）已知 ＝ ，则 的值为 。  分式的四则运算与分式的乘方 1）分式的乘除法法则： 用分子的积作为积的分子，分母的积作为积的分母。式子表示为： o ㌳ o分式除以分式：把除式的分子、分母颠倒位置后，与被除式相乘。式子表示为 o ㌳ o ㌳ o1．（2018 山东中考模拟）计算 2 2 ba a   的结果为（ ） A．b B． b C．  ab D． b a 2．（2018·山东中考模拟）化简 2 2 1x - ÷ 1 1x  的结果是( ) A． 2 1x  B． 2 x C． 2 1x  D．2(x＋1) 3．（2019·江西中考真题）计算 的结果为（ ） A． B． C． D． 4．（2019·天津中考模拟）计算 2 2 3 1 36 6 x x x x x    的结果为( ) A． 6x x  B． 6 x x  C． 6 x x  D． 6x  5．（2019·山东中考模拟）化简： 2( )n n m m m    的结果是（ ） A． 1m  B． 1m  C． mn m  D． mn n  6．（2019·河北中考模拟）化简 2 2 1 1 x ax   的结果是 2 1x  ，则 a 的值是（ ） A．1 B．﹣1 C．2 D．﹣2 2）分式的乘方：把分子、分母分别乘方。式子 o ㌳ o 注意： 1.分式乘方要把分子、分母分别乘方。 2.分式乘方时，要首先确定乘方结果的符号，负数的偶次方为正，负数的奇次方为负。 1．（2019·内蒙古中考模拟）计算：① 23 2 n m      _____；② b a a b a b    _____． 2．（2018·上海中考模拟）计算： （1）（ 23b a ）2=_____； （2） 2 10ab c 5 4 a c  =_____． 3．（2018·湖北中考模拟）计算： 32( )x y  =______． 3）分式的加减法则： 同分母分式加减法：分母不变，把分子相加减。式子表示为 o ㌳ o 异分母分式加减法：先通分，化为同分母的分式，然后再加减。式子表示为 o ㌳ o o 1．（2019·天津中考模拟）化简 2 1 1 1a a   的结果是( ) A． 3 1 a B． 3 1a  C． 1 1 a D． 1 1a  2．（2013·福建中考真题）计算 a 5 a 5 a 5   的结果是（ ） A．1 B．﹣1 C．0 D．a﹣5 4）整式与分式加减法：可以把整式当作一个整数，整式前面是负号，要加括号，看作是分母为 1 的分式， 再通分。 1．（2019·天津中考模拟）化简 2 ( 1)1 a aa   的结果是（ ） A． 2 1 1 a a   B． 1 1a   C． 2 1 1 a a   D． 1 1a  2．（2019·天津中考模拟）计算 4 +1x  5 的结果为（ ） A． 1x x   5 B． 1 5 x x   C． 5 x  5 D． 4 4x  3．（2019·广东中考模拟）计算：| 3 ﹣2|+ 2 3 1 ＝( ) A．﹣1 B．1 C．2 3 D．2 3 ﹣3 5)分式混合运算的运算 运算顺序：1.先把除法统一成乘法运算； 2.分子、分母中能分解因式的多项式分解因式； 3.确定分式的符号，然后约分； 4.结果应是最简分式. 1．（2019·北京中考模拟）已知 1 1(1 )1 1A x x     ，则 A＝( ) A． 2 1x x x   B． 2 1 x x  C． 2 1 1x  D．x2﹣1 2．（2019·四川中考真题）化简 2b a ba a a       的结果是( ) A．a-b B．a+b C． 1 a b D． 1 a b 3．（2019·河北中考模拟）若分式 运算结果为 ，则在“□”中添加的运算符号为( ) A．+ B．— C．—或÷ D．+或×  整数指数幂  ㌳  ㌳  o ㌳ o  ㌳ （ 0 ）  o ㌳ o  ㌳ （ 0 ）  0 ㌳ （ 0 ）（任何不等于零的数的零次幂都等于 1） 其中 m，n 均为整数。 1．（2018·山东中考模拟）下列计算正确的是（ ） A．a2•a3＝a6 B．（﹣2a）3＝﹣6a3 C． 3 2 24 6 3a a a  D．（3.14﹣π）0＝0 2．（2019·广西中考模拟）把实数 36.12 10 用小数表示为（ ） A．0.0612 B．6120 C．0.00612 D．612000 3．（2017·天津中考模拟）下列计算正确的是（ ） A．2÷2﹣1=-1 B． 3 4 12 4 2x x x    C．(﹣2x﹣2)﹣3=6x6 D． 2 2 2 73 4x x x    4．（2016·山东中考模拟）若 2x＝3,4y＝5，则 2x－2y 的值为( )． A． 3 5 B．－2 C． 3 5 5 D． 6 5  科学记数法 有了负整数指数幂后，小于 1 的正数也可以用科学记数法表示。即小于 1 的正数可以用科学记数法表示为 a×10-n 的形式.(1≤∣a∣＜10，n 是正整数) 注意： 1）1≤︱a︱＜10 2）n 是正整数，n 等于原数中左边第一个不为 0 的数字前面所有的 0 的个数。(包括小数点前面的 0） 1．（2019·山东中考模拟）生物学家发现了某种花粉的直径约为 0.0000036 毫米，数据 0.0000036 用科学记数 法表示正确的是（ ） A．3.6×10﹣5 B．0.36×10﹣5 C．3.6×10﹣6 D．0.36×10﹣6 2．（2019·湖南中考模拟）据《经济日报》2018 年 5 月 21 日报道：目前，世界集成电路生产技术水平最高 已达到 7nm（1nm=10﹣9m），主流生产线的技术水平为 14～28nm，中国大陆集成电路生产技术水平最高为 28nm．将 28nm 用科学记数法可表示为（ ） A．28×10﹣9m B．2.8×10﹣8m C．28×109m D．2.8×108m 3．（2019·河南中考模拟）全球芯片制造已经进入 10 纳米到 7 纳米器件的量产时代．中国自主研发的第一台 7 纳米刻蚀机，是芯片制造和微观加工最核心的设备之一，7 纳米就是 0.000000007 米．数据 0.000000007 用科学记数法表示为（ ） A．0.7×10﹣8 B．7×10﹣8 C．7×10﹣9 D．7×10﹣10 考查题型三 分式的化简求值 1．（2019·湖北中考真题）已知二元一次方程组 1 2 4 9 x y x y      ，则 2 2 2 2 2x xy y x y    的值是（ ） A． 5 B．5 C． 6 D．6 2．（2019·北京中考模拟）如果 3 0x y  ，那么代数式  2 2 2 2 x y x yx xy y     的值为（ ） A． 2 7  B． 2 7 C． 7 2  D． 7 2 3．（2019·天津二十中中考模拟）已知 1 1 1 2a b   ，则 ab a b 的值是（ ） A． 1 2 B．－ 1 2 C．2 D．－2 4．（2019·北京中考模拟）如果 a+b＝ 1 2 ，那么 a b a b b a   2 2 的值是（ ） A． 1 2 B． 1 4 C．2 D．4 5．（2018·北京中考模拟）如果 2 2 2 0m m   ，那么代数式 24 4 2 m mm m m       的值是( ) A． 2 B． 1 C．2 D．3 知识点三 分式方程 解分式方程的基本 1）去分母(两边同乘最简公分母，约去分母，化成整式方程)。 2）解整式方程(去括号-移项/合并同类项-系数化为 1)。 3）检验(把整式方程的解代入最简公分母， 若最简公分母为 0 ，则 x=a 不是分式方程的解 若最简公分母不为 0，则 x=a 是分式方程的解 4）写出答案 1．（2019·山东中考真题）解分式方程 1 1 22 2 x x x     时，去分母变形正确的是（ ） A．  1 1 2 2x x      B．  1 1 2 2x x    C．  1 1 2 2x x     D．  1 1 2 2x x     2．（2018·辽宁中考模拟）方程 2 3x  ＝ 1 1x  的解为( ) A．x＝3 B．x＝4 C．x＝5 D．x＝﹣5 3．（2019·山东中考模拟）解分式方程 2 x 2 3x 1 1 x    时，去分母后变形为（ ） A．    2 x 2 3 x 1    B．  2 x 2 3 x 1    C．    2 x 2 3 1  x    D．    2 x 2 3 x 1    增根的概念：在分式方程化为整式方程的过程时，若整式方程的根使最简公分母为 0（即根使整式方程成立， 但分式方程中分母为 0 ），那么这个根叫做原分式方程的增根。 考查题型四 根据分式方程的解确定字母参数的方法 1．（2018·山东中考模拟）若关于 x 的分式方程 1 1 m x   =2 的解为非负数，则 m 的取值范围是（ ） A．m＞﹣1 B．m≥1 C．m＞﹣1 且 m≠1 D．m≥﹣1 且 m≠1 2．（2019·云南中考模拟）已知关于 x 的分式方程 + =1 的解是非负数，则 m 的取值范围是（ ） A．m＞2 B．m≥2 C．m≥2 且 m≠3 D．m＞2 且 m≠3 3．（2018·黑龙江中考模拟）已知关于 x 的分式方程 a 2 1x 1   的解是非正数，则 a 的取值范围是（ ） A．a≤﹣1 B．a≤﹣1 且 a≠﹣2 C．a≤1 且 a≠﹣2 D．a≤1 考查题型五 根据分式方程的增根确定字母参数的方法 1．（2017·四川中考模拟）若关于 x 的方程 3 11 1 k x x    有增根，则 k 的值为( )． A．3 B．1 C．0 D．－1 2．（2018·四川中考真题）若分式方程 2 3 1 2 2 2 x a x x x x     有增根，则实数 a 的取值是（ ） A．0 或 2 B．4 C．8 D．4 或 8 3．（2018·四川中考真题）若 x=4 是分式方程 2 1 3 a x x    的根，则 a 的值为 ( ) A．6 B．－6 C．4 D．－4 分式方程解决实际问题的步骤： 1. 根据题意找等量关系 2. 设未知数 3. 列出方程 4. 解方程，并验根（对解分式方程尤为重要） 5. 写答案 考查题型六 列分式方程解决实际问题 1．（2019·河北中考模拟）甲、乙两人分别从距目的地 6 千米和 10 千米的两地同时出发，甲、乙的速度比是 3：4，结果甲比乙提前 20 分钟到达目的地，求甲、乙的速度．若设甲的速度为 3x 千米/时，乙的速度为 4x 千米/时．则所列方程是( ) A． 6 3x +20= 10 4x B． 6 3x ＝ 10 4x +20 C． 6 3x + 20 60 ＝ 10 4x D． 6 3x ＝ 10 4x + 20 60 2．（2019·新疆中考模拟）A、B 两地相距 48 千米，一艘轮船从 A 地顺流航行至 B 地，又立即从 B 地逆流 返回 A 地，共用去 9 小时，已知水流速度为 4 千米/时，若设该轮船在静水中的速度为 x 千米/时，则可列方 程（ ） A． 48 48 94 4x x    ； B． 48 48 94 4x x    ； C． 48 x +4=9； D． 96 96 94 4x x    ； 考查题型七 列分式方程解决行程问题 1．（2019·新疆中考模拟）某市为解决部分市民冬季集中取暖问题，需铺设一条长 4000 米的管道，为尽量减 少施工对交通造成的影响，施工时“…”，设实际每天铺设管道 x 米，则可得方程 4000 4000 10x x  ＝20，根据 此情景，题中用“…”表示的缺失的条件应补为（ ） A．每天比原计划多铺设 10 米，结果延期 20 天完成 B．每天比原计划少铺设 10 米，结果延期 20 天完成 C．每天比原计划多铺设 10 米，结果提前 20 天完成 D．每天比原计划少铺设 10 米，结果提前 20 天完成 2．（2018·辽宁中考模拟）施工队要铺设一段全长 2000 米的管道，因在中考期间需停工两天，实际每天施工 需比原来计划多 50 米，才能按时完成任务，求原计划每天施工多少米．设原计划每天施工 x 米，则根据题 意所列方程正确的是（ ） A． 2000 2000 250x x   B． 2000 2000 250x x   C． 2000 2000 250x x   D． 2000 2000 250x x   考查题型八 列分式方程解决工程问题 1．（2016·山东中考模拟）小明上月在某文具店正好用 20 元钱买了几本笔记本，本月再去买时，恰遇此文 具店搞优惠酬宾活动，同样的笔记本，每本比上月便宜 1 元，结果小明只比上次多用了 4 元钱， 却比上 次多买了 2 本．若设他上月买了 x 本笔记本，则根据题意可列方程（ ） A． 24 x 2 - 20  x =1 B． 20 x - 24 x 2 =1 C． 24 x - 20 x 2 =1 D． 20 x 2 - 24  x =1 2.（2019·尉氏县十八里镇实验中学中考模拟）“五一”期间，某中学数学兴趣小组的同学们租一辆小型巴士 前去某地进行社会实践活动，租车租价为 180 元．出发时又增加了两位同学，结果每位同学比原来少分摊 了 3 元车费．若小组原有 x 人，则所列方程为（ ） A．180 180 32x x   B． 180 180 32x x   C． 180 180 32x x   D． 180 180 32x x   考查题型九 分式方程与不等式结合解决实际问题 1．（2017·广西中考模拟）学校计划选购甲、乙两种图书作为“校园读书节”的奖品．已知甲图书的单价是乙 图书单价的 1.5 倍；用 600 元单独购买甲种图书比单独购买乙种图书要少 10 本． （1）甲、乙两种图书的单价分别为多少元？ （2）若学校计划购买这两种图书共 40 本，且投入的经费不超过 1050 元，要使购买的甲种图书数量不少于 乙种图书的数量，则共有几种购买方案？ 2.（2019·辽宁中考真题）某超市用 1200 元购进一批甲玩具，用 800 元购进一批乙玩具，所购甲玩具件数是 乙玩具件数的 5 4 ，已知甲玩具的进货单价比乙玩具的进货单价多 1 元． （1）求：甲、乙玩具的进货单价各是多少元？ （2）玩具售完后，超市决定再次购进甲、乙玩具（甲、乙玩具的进货单价不变），购进乙玩具的件数比甲 玩具件数的 2 倍多 60 件，求：该超市用不超过 2100 元最多可以采购甲玩具多少件？