北师大版九年级上册数学第一章测试题附答案 16页

北师大版九年级上册数学第一章测试题附答案 ‎(满分：120分　　　考试时间：120分钟)‎ 一、选择题(本大题共6小题，每小题3分，共18分)‎ ‎1．矩形、菱形、正方形都具有的性质是（ C ）‎ A．每一条对角线平分一组对角 B．对角线相等 C．对角线互相平分 D．对角线互相垂直 ‎2．如图，在Rt△ABC中，CD是斜边AB上的中线，若AB＝8，则CD的长是（ C ）‎ A．6 B．5 C．4 D．3‎ 第2题图第3题图第5题图　‎ ‎3．如图，在矩形ABCD中，对角线AC，BD相交于点O，∠ACB＝30°，则∠AOB的大小为(　B　)‎ A．30° B．60° C．90° D．120°‎ ‎4．在▱ABCD中，AB＝3，BC＝4，当▱ABCD的面积最大时，下列结论正确的有（ B ）‎ ‎①AC＝5　 ②∠A＋∠C＝180°　 ③AC⊥BD　④AC＝BD A．①②③ B．①②④ C．②③④ D．①③④‎ ‎5．(2018·宿迁)如图，菱形ABCD的对角线AC，BD相交于点O，点E为边CD的中点，若菱形ABCD的周长为16，∠BAD＝60°，则△OCE的面积是(　A　)‎ A. B．2 C．2 D．4‎ ‎6．如图，正方形ABCD的面积为4，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD＋PE的和最小，则这个最小值为A A．2 B．3 C．2 D. 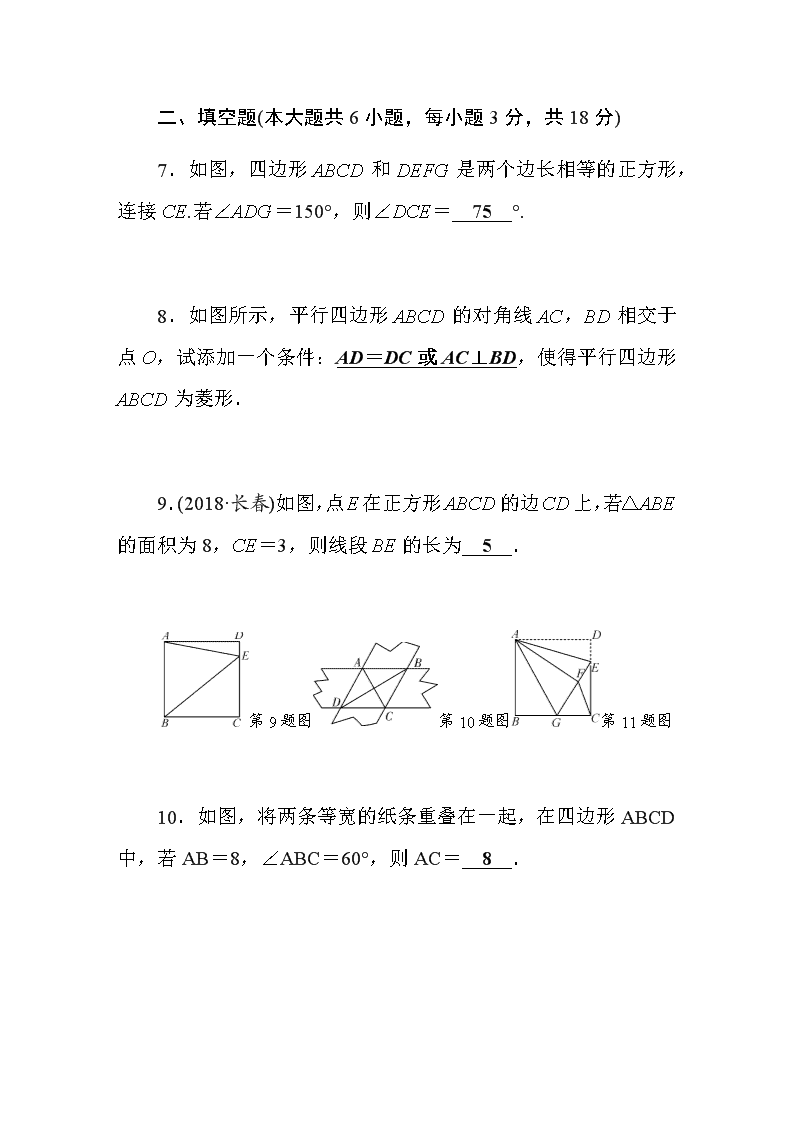第6题图第7题图第8题图 二、填空题(本大题共6小题，每小题3分，共18分)‎ ‎7．如图，四边形ABCD和DEFG是两个边长相等的正方形，连接CE.若∠ADG＝150°，则∠DCE＝ 75 °.‎ ‎8．如图所示，平行四边形ABCD的对角线AC，BD相交于点O，试添加一个条件：AD＝DC或AC⊥BD，使得平行四边形ABCD为菱形．‎ ‎9．(2018·长春)如图，点E在正方形ABCD的边CD上，若△ABE的面积为8，CE＝3，则线段BE的长为 5 ．‎ 第9题图第10题图第11题图 ‎10．如图，将两条等宽的纸条重叠在一起，在四边形ABCD中，若AB＝8，∠ABC＝60°，则AC＝ 8 ．‎ ‎11．如图，在正方形ABCD中，AB＝6，点E在边CD上，且CD＝3DE，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG，CF，则下列结论：‎ ‎①△ABG≌△AFG；②BG＝CG；③AG∥CF；④S△EGC＝S△AFE；⑤∠AGB＋∠AED＝145°，其中正确的序号有①②③④.‎ ‎12．菱形AOBC如图放置，A(3，4)，先将菱形向左平移9个单位长度，再向下平移1个单位，然后沿x轴翻折，最后绕坐标轴原点O旋转90°得到点C的对应点为点P，则点P的坐标为(－3，1)或(3，－1)．‎ 三、(本大题共5小题，每小题6分，共30分)‎ ‎13．如图，在菱形ABCD中，点E，F分别为边CD，AD的中点，连接AE，CF.求证：△ADE≌△CDF.‎ 证明：∵四边形ABCD是菱形，‎ ‎∴AD＝DC，又∵E，F为CD，AD的中点，‎ ‎∴DF＝AD，DE＝DC，∴DF＝DE.又∵∠ADE＝∠CDF，‎ ‎∴△ADE≌△CDF(SAS)．‎ ‎14．(2018·张家界)如图，在矩形ABCD中，点E在BC上，AE＝AD，DF⊥AE，垂足为点F.‎ ‎(1)求证：DF＝AB；‎ ‎(2)若∠FDC＝30°，且AB＝4，求AD.‎ ‎(1)证明：在矩形ABCD中，AD∥BC，‎ ‎∴∠DAF＝∠AEB.又∵DF⊥AE，‎ ‎∴∠DFA＝90°，∴∠DFA＝∠B.‎ 又∵AD＝EA，‎ ‎∴△ADF≌△EAB(AAS)，∴DF＝AB.‎ ‎(2)解：∵∠DAF＋∠ADF＝90°，∠FDC＋∠ADF＝90°，‎ ‎∴∠DAF＝∠FDC＝30°，∴AD＝2DF.又∵DF＝AB＝4，‎ ‎∴AD＝2AB＝2×4＝8.‎ ‎15．如图，在▱ABCD中，点E，F在直线AC上(点E在F点左侧)，BE∥DF.‎ ‎(1)求证：四边形BEDF是平行四边形；‎ ‎(2)若AB⊥AC，AB＝4，BC＝2，当四边形BEDF为矩形时，求线段AE的长．‎ ‎(1)证明：连接BD，交AC于点O，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴OB＝OD.由BE∥DF得∠BEO＝∠DFO.‎ 又∵∠EOB＝∠FOD，∴△BEO≌△DFO，‎ ‎∴BE＝DF，又∵BE∥DF，∴四边形BEDF是平行四边形；‎ ‎(2)解：∵AB⊥AC，AB＝4，BC＝2，‎ ‎∴AC＝6，∴AO＝3，∴在Rt△BAO中，BO＝5.‎ ‎∵四边形BEDF是矩形，∴OE＝OB＝5.‎ ‎∴点E在OA的延长线上，∴AE＝2.‎ ‎16．如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，E是AC的中点，EF平分∠BED.求证：EF⊥BD.‎ 证明：∵∠ABC＝∠ADC＝90°，‎ ‎∴△ABC和△ADC都是直角三角形．‎ 又∵E是AC的中点，∴BE＝DE＝AC.‎ 又∵EF平分∠BED，∴EF⊥BD.‎ ‎17．如图，以正方形ABCD的对角线AC为一边，延长AB到E，使AE＝AC，以AE为一边作菱形AEFC，若菱形的面积为9，求正方形的边长．‎ 解：设正方形的边长为x.‎ ‎∵AC为正方形ABCD的对角线，‎ ‎∴AC＝x，∴AE＝x，CB＝x，‎ ‎∴S菱形AEFC＝AE·CB＝x·x＝x2＝9，‎ 解得x＝±3，依题意舍去x＝－3，即正方形的边长为3.‎ 四、(本大题共3小题，每小题8分，共24分)‎ ‎18．(哈尔滨中考)如图，已知在正方形ABCD中，点E在边CD上，AQ⊥BE于点Q，DP⊥AQ于点P.‎ ‎(1)求证：AP＝BQ；‎ ‎(2)在不添加任何辅助线的情况下，请直接写出图中四对线段，使每对中较长线段与较短线段长度的差等于PQ的长．‎ ‎(1)证明：∵正方形ABCD，∴AD＝BA，∠BAD＝90 °，即∠BAQ＋∠DAP＝90 °.∵DP⊥AQ，‎ ‎∴∠ADP＋∠DAP＝90 °，∴∠BAQ＝∠ADP.‎ ‎∵AQ⊥BE于点Q，DP⊥AQ于点P，∴∠AQB＝∠DPA＝90 °，∴△AQB≌△DPA(AAS)，∴AP＝BQ；‎ ‎(2)解：①AQ－AP＝PQ；②AQ－BQ＝PQ；③DP－AP＝PQ；④DP－BQ＝PQ.‎ ‎19．已知：如图，在菱形ABCD中，点E，O，F分别为AB，AC，AD的中点，连接CE，CF，OE，OF.‎ ‎(1)求证：△BCE≌△DCF；‎ ‎(2)当AB与BC满足什么关系时，四边形AEOF是正方形？请说明理由．‎ ‎(1)证明：∵四边形ABCD是菱形，‎ ‎∴AB＝BC＝CD＝AD，∠B＝∠D.‎ ‎∵点E，F分别为AB，AD的中点，‎ ‎∴BE＝DF，‎ ‎∴△BCE≌△DCF(SAS)；‎ ‎(2)解：当AB⊥BC时，四边形AEOF是正方形．‎ 理由如下：‎ 由(1)得AE＝OE＝OF＝AF，‎ ‎∴四边形AEOF是菱形．‎ ‎∵AB⊥BC，OE∥BC，‎ ‎∴OE⊥AB，‎ ‎∴∠AEO＝90°，‎ ‎∴四边形AEOF是正方形．‎ ‎20．如图，O是矩形ABCD的对角线的交点，E，F，G，H 分别是OA，OB，OC，OD上的一点，且AE＝BF＝CG＝DH.‎ ‎(1)求证：四边形EFGH是矩形；‎ ‎(2)若E，F，G，H分别是OA，OB，OC，OD的中点，且DG⊥AC，OF＝2 cm，求矩形ABCD的面积．‎ ‎(1)证明：∵四边形ABCD是矩形，‎ ‎∴OA＝OB＝OC＝OD.‎ ‎∵AE＝BF＝CG＝DH，‎ ‎∴AO－AE＝OB－BF＝CO－CG＝DO－DH，‎ 即OE＝OF＝OG＝OH，‎ ‎∴四边形EFGH是矩形．‎ ‎(2)解：∵G是OC的中点，‎ ‎∴GO＝GC.‎ ‎∵DG⊥AC，∴DG为OC的垂直平分线．‎ ‎∴CD＝OD.‎ ‎∵F是BO的中点，OF＝2 cm，‎ ‎∴BO＝4 cm.‎ ‎∵四边形ABCD是矩形，‎ ‎∴DO＝BO＝4 cm，‎ ‎∴DC＝4 cm，DB＝8 cm，‎ ‎∴CB＝＝4，‎ ‎∴矩形ABCD的面积＝4×4＝16 cm2.‎ 五、(本大题共2小题，每小题9分，共18分)‎ ‎21．(新疆中考)如图，▱ABCD中，AB＝2，AD＝1，∠ADC＝60°，将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，折痕交CD边于点E.‎ ‎(1)求证：四边形BCED′是菱形；‎ ‎(2)若点P是直线l上的一个动点，请计算PD′＋PB的最小值．‎ ‎(1)证明：如图①，在▱ABCD中，∵∠D＝60 °，∠DAB＝∠1＋∠2＝120 °.由题意知△ADE≌△AD′E，∴∠1＝∠2＝∠D ‎＝60 °，∴△DEA和△AD′E是等边三角形，∴DE＝AD′＝AD＝ED′＝1.∵AB＝2，∴D′B＝1.同理EC＝1，∴EC＝D′B＝ED′＝1.∵四边形ABCD是平行四边形，∴EC∥D′B，∴四边形D′BCE是平行四边形．又∵D′B＝ED′，∴▱BCED′是菱形；‎ ‎①　　　②‎ ‎(2) 解：如图②，BD的长即为所求，作DG⊥BA的延长线于点G.∵∠DAB＝120 °，∴∠DAG＝60 °，∵∠G＝90 °，∴∠ADG＝30 °.在Rt△ADG中，∵AD＝1，∴AG＝，DG＝.∵AB＝2，∴BG＝.在Rt△BDG中，BD2＝BG2＋DG2＝7，∴BD＝，即PD′＋PB＝.‎ ‎22．已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．‎ ‎(1)求证：△ABM≌△DCM；‎ ‎(2)判断四边形MENF是什么特殊四边形，并证明你的结论；‎ ‎(3)当AD∶AB＝____时，四边形MENF是正方形，并说明理由．‎ ‎(1)证明：∵四边形ABCD是矩形，‎ ‎∴AB＝CD，∠A＝∠D＝90 °.‎ 又∵M是AD的中点，∴AM＝DM.在△ABM和△DCM中，∴△ABM≌△DCM(SAS)；‎ ‎(2)解：四边形MENF是菱形，证明略；‎ ‎(3)解：当AD∶AB＝2∶1时，四边形MENF是正方形．理由：‎ ‎∵M为AD中点，∴AD＝2AM.∵AD∶AB＝2∶1，‎ ‎∴AM＝AB.∵∠A＝90 °，∴∠ABM＝∠AMB＝45 °.‎ 同理：∠DMC＝45 °.∴∠EMF＝180 °－45 °－45 °＝90 °.‎ ‎∵四边形MENF是菱形，∴四边形MENF是正方形．‎ 六、(本大题共12分)‎ ‎23．如图①分别是可活动的菱形和平行四边形学具，已知平行四边形较短的边与菱形的边长相等．‎ ‎①②　③‎ ‎　‎ ‎(1)在一次数学活动中，某小组学生将菱形的一边与平行四边形较短边重合，摆拼成如图②所示的图形，AF经过点C，连接DE交AF于点M，观察发现：点M是DE的中点．‎ 下面是两位学生有代表性的证明思路：‎ 思路1：不需作辅助线，直接证明三角形全等；‎ 思路2：不证三角形全等，连接BD交AF于点H.‎ ‎……‎ 请参考上面的思路，证明点M是DE的中点(只需用一种方法证明)；‎ ‎(2)如图③，在(1)的前提下，当∠ABE＝135°时，延长AD，EF交于点N，求的值；‎ ‎(3)在(2)的条件下，若＝k(k为大于的常数)，直接用含k的代数式表示的值．‎ ‎(1)证明：思路一：∵AB＝CD，AB∥CD，又∵‎ 四边形ABEF是平行四边形，∴AB＝EF，AB∥EF，∴CD＝EF，CD∥EF，∴∠CDM＝∠FEM，又∠DMC＝∠EMF，∴可证△CDM≌△FEM，∴DM＝EM，∴点M是DE的中点．‎ 思路二：证明：∵四边形ABCD是菱形，∴DH＝BH.又∵AF∥BE，∴HM∥BE，∴＝＝1，∴DM＝EM.∴点M是DE的中点．‎ ‎(2)解：∵△CDM≌△FEM，∴CM＝FM，设AD＝a，CM＝b，‎ ‎∵∠ABE＝135°，AF∥BE，∴∠BAF＝45°＝∠NAF，∴四边形ABCD为正方形，∴AC＝AD＝a.∵AB∥EF，∴∠AFN＝∠BAF＝45°，∴△ANF为等腰直角三角形，∴NF＝AF＝(a＋b＋b)＝a＋b，NE＝a＋b＋a＝2a＋b，∴＝＝＝.‎ ‎(3)解：∵＝＝＋2×＝k，∴＝(k－)，‎ ‎∴＝＝×＋1＝×＋1＝ .‎