2020-2021学年新初三数学上册知识点讲解 正多边形和圆、弧长和扇形的面积 22页

2020-2021 学年新初三数学上册知识点讲解 正多边形和圆、弧长和扇形的 面积 专题 07 正多边形和圆、弧长和扇形的面积专题详解 ................................................................................................1 24.3 正多边形和圆 ..............................................................................................................................................................2 知识框架 .............................................................................................................................................................................2 一、基础知识点 ...............................................................................................................................................................2 知识点 1 正多边形与圆的相关概念 .............................................................................................................................. 2 知识点 2 正多边形中各元素间的关系 ......................................................................................................................... 3 二、典型题型 ....................................................................................................................................................................5 题型 1 正多边形有关计算 ................................................................................................................................................ 5 24.4 弧长和扇形的面积 .....................................................................................................................................................8 知识框架 .............................................................................................................................................................................8 一、基础知识点 ...............................................................................................................................................................8 知识点 1 弧长公式 .............................................................................................................................................................. 8 知识点 2 扇形面积公式 ..................................................................................................................................................... 8 知识点 3 弓形面积 .............................................................................................................................................................. 9 知识点 4 圆锥的侧面展开图 ......................................................................................................................................... 10 二、典型题型 ................................................................................................................................................................. 12 题型 1 弧长、扇形面积、圆锥侧面积计算 .............................................................................................................. 12 题型 2 不规则图形面积 ................................................................................................................................................... 16 三、难点题型 ................................................................................................................................................................. 21 题型 1 最短距离................................................................................................................................................................. 21 24.3 正多边形和圆 知识框架 { 基础知识点 { 正多边形与圆的相关概念 正多边形中各元素间的关系 典型题型{正多边形有关计算 一、基础知识点 知识点 1 正多边形与圆的相关概念 1）正多边形：各边、各角都相等的多边形 注：正多边形必须同时满足 2 个条件： ①每一条边都相等； ②每一个角都相等 2）正多边形的中心：正多边形外接圆的圆心 正多边形的半径：正多边形外接圆的半径 正多边形的边心距：中心到正多边形的一边的距离 正多边形的中心角：正多边形每一边所对的外接圆的圆心角 3）正多边形都是轴对称图形，共有 n 条对称轴，每条对称轴都经过它的中心，当 n 为偶数时， 正 n 边形还是中心对称图形。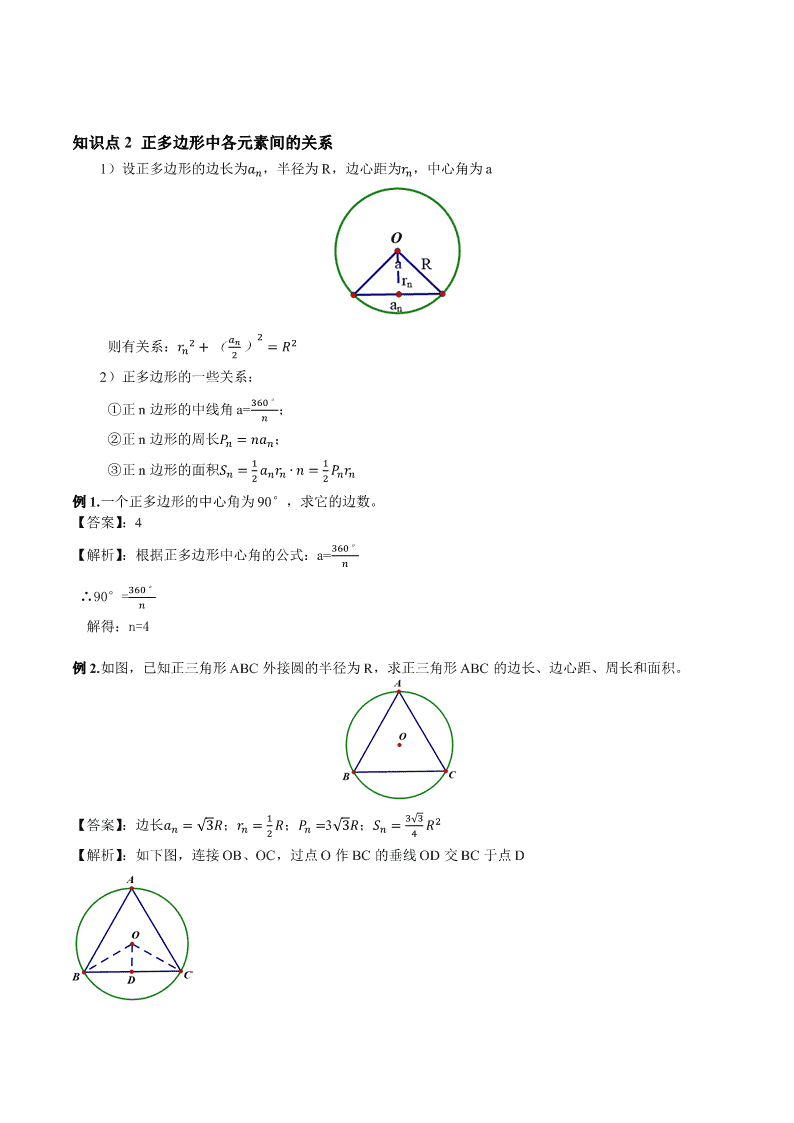 例 1.下列多边形中，是正多边形的是（ ） A.菱形 B.矩形 C.等腰梯形 D.正六边形 【答案】：D 【解析】：正多边形需满足 2 个条件：每条边相等；每个角相等 A.菱形仅边相等，角不等，不为正多边形； B.矩形角都相等，但边互等，不为正多边形； C.等腰梯形边和角都不等，不为正多边形； D.正六边形满足条件，是正多边形 例 2.下列多边形中，既是轴对称图形，又是中心对称图形的是（ ） A.正三角形 B.正方形 C.正五边形 D.平行四边形 【答案】：B 【解析】：正多边形，且边数 n 为偶数时，图形既是轴对称图形，又是中心对称图形 ∴正方形为正四边形，n=4，符合 ∴答案为 B 知识点 2 正多边形中各元素间的关系 1）设正多边形的边长为푎푛，半径为 R，边心距为푟푛，中心角为 a 则有关系：푟푛2 + （ 푎푛 2 ）2 = 푅2 2）正多边形的一些关系： ①正 n 边形的中线角 a=360° 푛 ； ②正 n 边形的周长푃푛 = 푛푎푛； ③正 n 边形的面积푆푛 = 1 2 푎푛푟푛 ∙ 푛 = 1 2 푃푛푟푛 例 1.一个正多边形的中心角为 90°，求它的边数。 【答案】：4 【解析】：根据正多边形中心角的公式：a=360° 푛 ∴90°=360° 푛 解得：n=4 例 2.如图，已知正三角形 ABC 外接圆的半径为 R，求正三角形 ABC 的边长、边心距、周长和面积。 【答案】：边长푎푛 = √3푅；푟푛 = 1 2 푅；푃푛 =3√3푅；푆푛 = 3√3 4 푅2 【解析】：如下图，连接 OB、OC，过点 O 作 BC 的垂线 OD 交 BC 于点 D ∵△ABC 为正三角形，半径为 R ∴OB=OC=R，∠OBC=∠OCB=1 2 ∙ 60° = 30° ∴△BOD 是含 30°角的直角三角形 ∴OD=1 2 푅 = 푟푛，BD=√3 2 푅 ∴BC=√3푅 = 푎푛 ∴푃푛 = 3 ∙ 푎푛 =3√3푅 푆△퐵푂퐶 = 1 2 ∙ BC ∙ OD = 1 2 ∙ √3푅 ∙ 1 2 푅 = √3 4 푅2 ∴푆푛 = 3푆△퐵푂퐶 = 3√3 4 푅2 二、典型题型 题型 1 正多边形有关计算 解题技巧：正多边形的计算是，主要是多边形各元素间关系的转化与计算。主要方法为：连接正多边形的中 心和顶点，并过中心作边的垂线，构造直角三角形，再利用相关几何知识计算求解。 常用的几何知识有： ①勾股定理；②垂径定理 例 1.如图，正六边形 ABCDEF 内接于O，半径为 4，求这个正六边形边心距 OH 的长。 【答案】：2√3 【解析】：如下图，连 OC ∵是正六边形 ABCDEF ∴圆心角 a=360° 6 = 60° ∴∠HOC=30° ∵半径为 4 ∴OC=4 ∴HC=2，OH=2√3 例 2.已知O 的面积为 2휋，求其内接正三角形的面积。 【答案】：3 2 √3 【解析】：如下图，连 OC，连 AO，并延长 AO 交 BC 于点 D ∵O 的面积为 2휋 ∴2휋 = 휋 ∙ 푅2，解得：R=√2 ∵△ABC 是正三角形 ∴∠ACB=∠BAC=60°，且 AD⊥BC，点 D 为 BC 的中点 ∴∠OCD=30°，∠DAC=30° ∴OD=1 2 푅 = √2 2 ，DC=√3 2 푅 = √6 2 ∴BC=√6，AD=√3 2 퐷퐶 = 3√2 2 ∴푆△퐴퐵퐶 = 1 2 ∙ 퐵퐶 ∙ 퐴퐷 = 1 2 ∙ √6 ∙ 3√2 2 = 3 2 √3 例 3.如图，五边形 ABCDE 是O 的内接正五边形，对角线 AC、BD 相交于点 P，下列结论正确的有 。 ①∠BAC=36°；②PB=PC；③四边形 APDE 是菱形 【答案】：①、②、③ 【解析】：∵ABCDE 是正五边形 ∴∠ABC=（5－2）×180° 5 = 108° ∵AB=BC，∴△ABC 是等腰三角形 ∴∠BAC=∠BCA=36°，①正确 ∵퐴퐵̂ = 퐶퐷̂ ∴∠BCA=∠CBD=36° ∴△BCP 为等腰三角形 ∴PB=PC，②正确 ∴∠PAE=72° ∵∠E=108° ∴AP∥ED 同理，PD∥AE ∴四边形 AEDP 为平行四边形 ∵AE=ED ∴平行四边形 AEDP 为菱形，③正确 例4.如图，正三角形的边长为12cm，剪去三个角后成为一个正六边形，则这个正六边形的内部任意一点到 各边的距离和为 cm． 【答案】：12√3 【解析】：如下图，过多边形的中心O作DC的垂线交DC于点G，连接OD，OC ∵正三角形边长为12 ∴正六边形的边长为4 ∴CG=2，OC=4 ∴OG=2√3 ∴푆△퐷푂퐶 = 1 2 × 4 × 2√3 = 4√3 ∴正六边形的面积为：6×4√3 = 24√3 取正多边形ABCDEF内任意点M，过点M分别作DC，DE，EF，FA，AB，BC的垂线，设垂线距离分别为h1，h2，h3， h4，h5，h6 则正多边形的面积为： 1 2 × 4 × ℎ1 + 1 2 × 4 × ℎ2 + 1 2 × 4 × ℎ3 + 1 2 × 4 × ℎ4 + 1 2 × 4 × ℎ5 + 1 2 × 4 × ℎ6 =1 2 × 4 × (h1 + h2 + h3 + h4 + h5 + h6)= 24√3 ∴h1 + h2 + h3 + h4 + h5 + h6 =12√3 例5.有一个内角为60°的菱形的面积是8√3 ，则它的内切圆的半径为 ___________ 【答案】：√3 【解析】：如图，设∠B=60° 在△ABC 中，△ABC 为正三角形，面积为 4√3 设 BC=x，则 EC=1 2 푥，AE=√3 2 x 则1 2 ∙ 푥 ∙ √3 2 =4√3 解得：x=4 过棱形 ABCD 的中心（对角线交点）O，作 OF⊥BC 交 BC 于点 F 则 OF 即内切圆的半径 r ∵푆△퐴퐵퐶 =4√3 ∴푆△푂퐵퐶 =2√3=1 2 ∙ 4 ∙ r 解得：r=√3 24.4 弧长和扇形的面积 知识框架 { 基础知识点 { 弧长公式 扇形面积公式 弓形面积 圆锥的侧面展开图 典型题型 { 弧长、扇形面积、圆锥侧面积计算{ 弧长有关计算 扇形面积有关计算 圆锥侧面积有关计算 不规则图形面积 { 割补法 等积变换 图形变换 难点题型{最短距离 一、基础知识点 知识点 1 弧长公式 1）弧长푙与 n°圆心角的关系：푙=2πR ∙ 푛° 360°，公式不可强记，通过比例关系推导： 弧长푙=圆的周长× 푛° 360°（n°圆心角的弧所占整个圆的比例） 即：푙=2πR ∙ 푛° 360° 例 1.一个扇形的圆心角为 120°，半径为 1，求此扇形的弧长。 【答案】：2 3 휋 【解析】：根据弧长公式：푙=2πR ∙ 푛° 360° =2π ∙ 1 ∙ 120° 360° = 2 3 휋 例 2.圆心角为 75°的扇形的弧长是 2.5휋，求扇形的半径。 【答案】：6 【解析】：根据弧长公式：푙=2πR ∙ 푛° 360° =2π ∙ R ∙ 75° 360° = 5 2 휋 ∴ 5 12 휋 ∙ R = 5 2 휋 解得：R=6 知识点 2 扇形面积公式 1）扇形面积 S 与 n°圆心角的关系：S=휋푅2 ∙ 푛° 360° 扇形面积 S=圆的面积× 푛° 360°（比例） 即：S=휋푅2 ∙ 푛° 360° 2）弧长和扇形面积合并，推导得：S=1 2 푙푅 S=휋푅2 ∙ 푛° 360° =2πR ∙ 푛° 360° ∙ 1 2 푅 = 1 2 푙푅 （便于记忆，可理解为三角形面积公式，푙—底；R—高） 例 1.一个扇形的圆心角是 120°，它的面积为 3π，求这个扇形的半径。 【答案】：3 【解析】：根据扇形面积公式：S=휋푅2 ∙ 푛° 360° = 휋푅2 ∙ 120° 360° = 3휋 化简得：1 3 휋푅2 = 3휋 解得：R=3 例 2.一个扇形面积为 3π，弧长为 2π，求圆心角。 【答案】：120° 【解析】：根据扇形公式：S= 1 2 푙푅 = 1 2 ∙ 2휋 ∙ 푅 = 3휋 解得：R=3 根据弧长公式：푙=2πR ∙ 푛° 360° =2π ∙ 3 ∙ n° 360° = 2휋 化简得： n° 360° = 1 3 解得：n=120 知识点 3 弓形面积 1）弓形面积可以看作使扇形面积和三角形面积的分解与组合，实际应用时，可根据图形直接选 用下列公式： ①当弓形所含的弧是劣弧时 有：푆弓 = 푆扇形푂퐴퐵 − 푆△푂퐴퐵 ②当弓形所含的弧时优弧时 有：푆弓 = 푆扇形푂퐴퐵 + 푆△푂퐴퐵 例 1.如图，扇形 AOB 的圆心角为 120°，半径为 2，求图中阴影部分的面积。 【答案】：4 3 휋 − √3 【解析】：根据图形，弓形面积=푆扇形푂퐴퐵 − 푆△푂퐴퐵，如下图，过点 O 作 AB 的垂线交 AB 于点 E ∵圆心角为 120°，根据扇形面积公式：푆扇形푂퐴퐵=휋푅2 ∙ 푛° 360° = π ∙ 22 ∙ 120° 360° = 4 3 π △AOB 为等腰三角形，∠AOB=120° ∴△OBE 和△BEA 为直角三角形（30°） ∵OB=2 ∴OE=1，BE=√3，AB=2√3 ∴푆△푂퐴퐵 = 1 2 ∙2√3 ∙ 1 = √3 ∴푆弓 = 4 3 휋 − √3 知识点 4 圆锥的侧面展开图 1）圆锥侧展开图与扇形的关系：圆锥的侧面展开是一个扇形，其半径等于圆锥的母线长，弧长 等于圆锥底面圆的周长。 2）圆锥高 h，母线푙与半径 r 关系：푟2 + ℎ2 = 푙2 3）圆锥底面半径为 r，母线长为푙，底面周长为 C，则侧面积 S=1 2 푙 ∙ C = 1 2 푙 ∙ 2πr = πr푙 4）圆锥全面积=侧面积+底面积=πr푙 + 휋푟2 注：圆锥的相关公式难以记忆，建议牢记圆锥与侧面展开图的图形形式，并理解侧面展开图与扇 形之间的关系。相关公式在解题过程中进行推导。 例 1.圆锥的母线长为 13，底面半径为 5，求圆锥的高。 【答案】：12 【解析】：圆锥的高线与底面半径垂直，母线为直角三角形的斜边 根据勾股定定理：52 + h2 = 132 解得：h=12 例 2.圆锥的底面半径为 3，高为 4，求圆锥的侧面展开图面积。 【答案】：15π 【解析】：∵圆锥底面半径 r=3，高 h=4 根据勾股定理，母线长푙 = 5 ∵r=3 ∴圆锥侧面展开弧长=2πr = 2π ∙ 3 = 6π ∴圆锥侧面展开图面积=1 2 ∙ 5 ∙ 6π = 15π 例 3.圆锥的高为 3√3，侧面展开图是半圆，求圆锥的侧面积。 【答案】：18π 【解析】：∵圆锥侧面展开的弧长 C=2πr 又∵圆锥侧面展开是半圆，C=1 2 ∙ 2π푙 ∴푙 = 2푟 ∵高 h=3√3，且有关系：푟2 + ℎ2 = 푙2 即：r2 + （3√3）2 = （2r）2 解得：r=3 圆锥侧面积=1 2 푙C = 1 2 ∙ 2r ∙ 2πr = 18π 二、典型题型 题型 1 弧长、扇形面积、圆锥侧面积计算 解题技巧：此类题型，需要紧紧抓公式． 弧长푙=2πR ∙ n° 360° （理解：圆的周长×扇形圆心角占整圆的比例） 扇形面积S=πR2 ∙ n° 360° （理解：圆的面积×扇形圆心角占整圆的比例） 推到得：扇形面积S＝1 2 푙R（理解：将扇形面积视为三角形面积，弧长径视为三角形的底，扇形的半径R 视为三角形的高，面积为１ ２ ×底×高） 圆锥侧面展开是扇形，扇形半径R为圆锥的母线长，扇形弧长为圆锥底面圆的周长，在求解圆锥问题 时，需理清这两个关系，再按照扇形公式进行求解． 解题步骤： ①根据题干要问题，确定要使用的公式； ②观察公式，确定未知量； ③根据题干和圆的相关特性，求解未知量； ④将未知量代入公式，完成计算。 一、弧长有关计算 例1.圆心角为75°的扇形的弧长是2.5π，则扇形的半径为 . 【答案】：6 【解析】：根据扇形弧长公式: 푙=2πR ∙ n° 360° 得: 2.5π=2πR ∙ 75° 360° 解得:R=6 例2.如图，四边形ABCD是O的内接圆，O的半径为2，∠B=135°，求퐴퐶̂ 的长。 【答案】：π 【解析】：∵∠B=135°，根据内接四边形的性质 ∴∠ADC=45° 根据圆心角与圆周角的关系 ∴∠AOC=90° 根据弧长公式：퐴퐶̂ =2πR ∙ n° 360° =2π ∙ 2 ∙ 90° 360°=π 例3.如图，等边△ABC的边长为4，D、E、F分别为边AB、BC、AC的中点，分别以A、B、C三点为圆心， 以AD长为半径作三条圆弧，则图中三条圆弧的弧长之和是（ ） A．π B．2π C．4π D．6π 【答案】：2π 【解析】：依题意，三个扇形是完全相同的扇形 扇形半径为等边三角形边长的一半2 扇形的圆心角为等边三角形的角为60° 根据弧长公式: 푙=2πR ∙ n° 360° 得: 每条弧长푙=2π ∙ 2 ∙ 60° 360°=2π 3 则三条弧长和为: 2π 3 ∙ 3 = 2π 例4.如图，在扇形AOB中，∠AOB=90°，点C为OA的中点，CD⊥OA交퐴퐵̂ 于D，若OA=2，求퐵퐷̂ 的长。 【答案】：π 3 【解析】：如下图，连接AD、OD ∵点C是AO的中点，CD⊥AO ∴CD是AO的垂直平分线 ∴AD=OD 又∵CD=AO=R ∴△AOD为等边三角形 ∴∠DOA=60° ∴∠DOB=30° 根据弧长公式：퐵퐷̂ =2πR ∙ n° 360° =2π ∙ 2 ∙ 30° 360°=π 3 二、扇形面积有关计算 例1.如图，边长为1的正方形ABCD，分别以A、C为圆心，边长为半径画弧，求第II部分的面积 【答案】：π 2 − 1 【解析】：∵푆扇퐵퐴퐷 = 푆퐼 + 푆퐼퐼，푆扇퐵퐶퐷 = 푆퐼퐼 + 푆퐼퐼퐼，푆正퐴퐵퐶퐷 = 푆퐼 + 푆퐼퐼 + 푆퐼퐼퐼 ∴푆扇퐵퐴퐷 + 푆扇퐵퐶퐷 − 푆正퐴퐵퐶퐷 = 푆퐼퐼 ∴푆퐼퐼 = π ∙ 12 ∙ 90° 360° + π ∙ 12 ∙ 90° 360° − 1 ∙ 1 = π 2 − 1 例2.如图，将半径为1，圆心角为120°的扇形OAB绕点A逆时针旋转一个角度，使点O的对应点D落在弧AB 上，点B的对应点为C，连接BC，则图中CD、BC和弧BD围成的封闭图形面积是（ ） A．√3 − π 6 B．√3 2 − π 6 C．√3 2 − π 8 D．√3 − π 3 - 【答案】：B 【解析】：如图，连接BD,OD ∵扇形的圆心角为120°,D为弧AB的中点 ∴∠AOD=∠BOD=60° ∵AO=OD=OB ∴△AOD和△ODB都为等边三角形,DB=OB=OA=DA=DC ∴∠ADO=∠ODB=60° ∴∠CDB=360°－120°－60°－60°=120° ∵DB=DC ∴△BDC为等腰三角形,∠DBC=∠DCB=30° 封闭图形的面积为:△BDC的面积+△OBD的面积－扇形OBD的面积 푆△BDC = √3 × 1 2 × 1 2 = √3 4 푆△OBD = 1 × √3 2 × 1 2 = √3 4 푆扇形OBD = 휋 × 12 × 60° 360° = 휋 6 封闭图形面积为: √3 4 + √3 4 − π 6 = √3 2 − π 6 ∴答案为B 三、圆锥侧面积有关计算 例1.现有一个圆心角为90°，半径为8cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），求 该圆锥底面圆的半径。 【答案】：2cm 【解析】：根据弧长公式：푙=2πR ∙ n° 360° = 2π ∙ 8 ∙ 90° 360° = 4π 扇形的弧长为圆锥底面圆的周长 ∴4π = 2πr 解得：r=2cm 例2.已知一个圆锥的侧面展开图是一个半径为9，圆心角为120°的扇形，求该圆锥的底面半径。 【答案】：3 【解析】：根据弧长公式：푙=2πR ∙ n° 360° = 2π ∙ 9 ∙ 120° 360° = 6π 扇形的弧长为圆锥底面圆的周长 ∴6π = 2πr 解得：r=3 例3.已知圆锥的侧面展开图是一个半圆，求这个半圆的母线长与底面半径的比值。 【答案】：2:1 【解析】：设母线长为R，即侧面展开的半圆（扇形）的半径为R，设圆锥底面半径为r 根据弧长公式：푙=2πR ∙ n° 360° = 2πR ∙ 180° 360° = πR ∵扇形的弧长为圆锥底面圆的周长 ∴πR = 2πr ∴R：r=2:1 例4.在长方形ABCD中，AB=16，如图所示裁出一个扇形ABE，将扇形围成一个圆锥（AB和AE重合），求 此圆锥的底面圆的半径。 【答案】：4 【解析】：根据弧长公式：푙=2πR ∙ n° 360° = 2π ∙ 16 ∙ 90° 360° = 8π ∵扇形的弧长为圆锥底面圆的周长 ∴8π = 2πr 解得：r=4 题型 2 不规则图形面积 一、割补法 解题技巧：将不规则图形的面积转化为几个已知图形的面积的和与差的形式。 例 1.如图，在等腰直角三角形 ABC 中，∠ACB=90°，AB=4√2，以 A 为圆心，AC 长为半 径作弧，交 AB 于点 D，求图中阴影部分的面积。 【答案】：8－2휋 【解析】：图形中阴影部分是不规则图形，需要割补 푆阴 = 푆△퐴퐵퐶 − 푆扇퐴퐶퐷 ∵△ABC 是等腰直角三角形，AB=4√2 ∴AC=BC=4 ∴푆△퐴퐵퐶 = 1 2 ∙ 4 ∙ 4 = 8 ∵∠CAD=45°，R=AC=4 ∴푆扇퐴퐶퐷 = 휋 ∙ 42 ∙ 45 360 = 2휋 ∴푆阴 =8－2휋 例 2.如图，AB 是O 的直径，C 是O 上一点，且 AC=2，∠CAB=30°，求图中阴影部分面积。 【答案】：√3 3 + 2 9 휋 【解析】：连接 OC，将阴影部分划分为△AOC 和扇形 COB 两部分 过点 O 作 AC 的垂线交 AC 于点 D ∵AC=2 根据垂径定理，AD=DC=1 ∵∠A=30° ∴OD=√3 3 ，OA=OC=OB=2√3 3 ，∠COB=60° 푆扇퐶푂퐵 = 휋 ∙ （ 2√3 3 ） 2 ∙ 60 360 = 2 9 휋 푆△퐴푂퐶 = 1 2 ∙ 2 ∙ √3 3 = √3 3 ∴푆阴 = √3 3 + 2 9 휋 二、等积变换 解题技巧：利用平行线间距离处处相等的性质，可将不规则图形等积转换处理。基本图形如 下，AB∥CD： ①푆△퐴퐵퐶 = 푆△퐴퐵퐷； ②푆△퐴퐶퐷 = 푆△퐵퐶퐷； ③푆△퐴푂퐶 = 푆△퐵푂퐷 例 1.如图，AB 为半圆 O 的直径，C，D 为半圆弧的三等分点，若 AB=12，求阴影部分的面积。 【答案】：6휋 【解析】：连接 CD、OC、OD ∵C、D 是半圆弧三等分点 ∴∠COA=∠COD=∠DOB=60° ∵OC=OD ∴△OCD 为等边三角形 ∴∠DCO=60°=∠COA ∴CD∥AB ∴푆△퐴퐶퐷 = 푆△퐶푂퐷 ∴푆阴 = 푆扇퐶푂퐷 = 휋 ∙ (12 2 ) 2 ∙ 60 360 = 6휋 例 2.如图，AB 是O 的直径，点 C 是 BA 延长线上一点，CD 切O 于 D 点，弦 DE∥CB，Q 是 AB 上一动点，CA=1，CD 是O 半径的√3倍。 （1）求O 的半径 R； （2）当 Q 从 A 向 B 运动的过程中，图中阴影部分的面积是否发生变化？ 【答案】：（1）1 （2）不变，为휋 6 【解析】：连接 OD、OE （1）∵CD 是O 的切线 ∴OD⊥CD ∵CD 是圆半径的√3倍，CA=1 ∴CD=√3푅，CO=R+1，DO=R 根据勾股定理：（√3푅）2 + 푅2 = （R + 1）2 解得：R=1 （2）∵OD=1，CO=2 ∴∠C=30°，∠DOC=60° ∵DE∥AB ∴∠EDO=60° ∵OD=OE ∴△ODE 为等边三角形 ∴∠DOE=30° ∵DE∥AB ∴푆△퐷푄퐸 = 푆△퐸푂퐷 ∴푆阴 = 푆扇퐷푂퐸 = 휋 ∙ 12 ∙ 60 360 = 휋 6 三、图形变换 解题技巧：通过平移，将一般图形转化为特殊图形。 例 1.如图，两个半圆中，长为 24 的弦 AB 与直径 CD 平行且与小半圆相切，那么图中阴影部分的面积 是多少？ 【答案】：72휋 【解析】：将小半圆向右平移，使得两个半圆的圆心重合，则阴影部分面积等于半圆环面积。过点 O 作 AB 的垂线，交 AB 于点 E，连接 AO。 根据垂径定理，AE=12 设大圆的半径为 R，小圆的半径为 r 则根据勾股定理：푅2 = 푟2 + 122 图中：푆阴 = 1 2 푆大圆 − 1 2 푆小圆 =1 2 휋 ∙ 푅2 − 1 2 휋 ∙ 푟2 =1 2 휋 ∙ （푅2 − 푟2） =1 2 휋 ∙ 122 =72휋 三、难点题型 题型 1 最短距离 解题技巧：圆锥侧面是立体图形，求两点之间的最短距离不好处理。解决此类问题，需要将圆锥的侧 面展开成扇形，则将立体图形转化为平面图形。平面图形上，两点之间的连线最短。 例 1.如图，已知圆锥的底面半径 r，母线长 OA=3r，C 为母线 OB 的中点，在圆锥的侧面上，求一只 蚂蚁从点 A 爬到点 C 的最短距离。 【答案】：3√3 2 푟 【解析】：∵圆锥底面半径为 r ∴圆锥底面周长 C=2휋r ∵圆锥底面周长等于侧面展开图弧长，设侧面展开图的圆心角为 n° ∴2휋r =2π ∙ 3r ∙ n° 360° ，解得：n=120° ∵点 B 是퐴퐴1̂ 的中点，∴∠BOA=60° ∵OA=OB，∴△OAB 为等边三角形 ∴OB=OA=AB=3r ∵点 C 是 OB 的中点 ∴CB=3푟 2 ，AC⊥OB ∴AC=3√3 2 푟 AC 即最短距离 例 2.已知圆锥的半径为 20，高 h=20√15。已知蚂蚁从底边上一点 A 出发，在侧面上爬行一圈又回到 A 点，求蚂蚁爬行的最短距离。 【答案】：80√2 【解析】：将圆锥的侧面展开，如下图所示。则最短距离即为 A퐴/ ∵h=20√15，r=20 ∴根据勾股定理，母线长푙 = 80 圆锥底面周长=2π ∙ 20 = 80π ∵圆锥底面周长与扇形弧长相等，设扇形圆心角为 n° ∴80π =2π ∙ 80 ∙ n° 360° ，解得：n=90° ∴△AE퐴/为等腰直角三角形 ∴A퐴/ =80√2