苏科版九年级10月质量调研考试数学试题(苏教版九年级数学上册10月月考测试卷) 7页

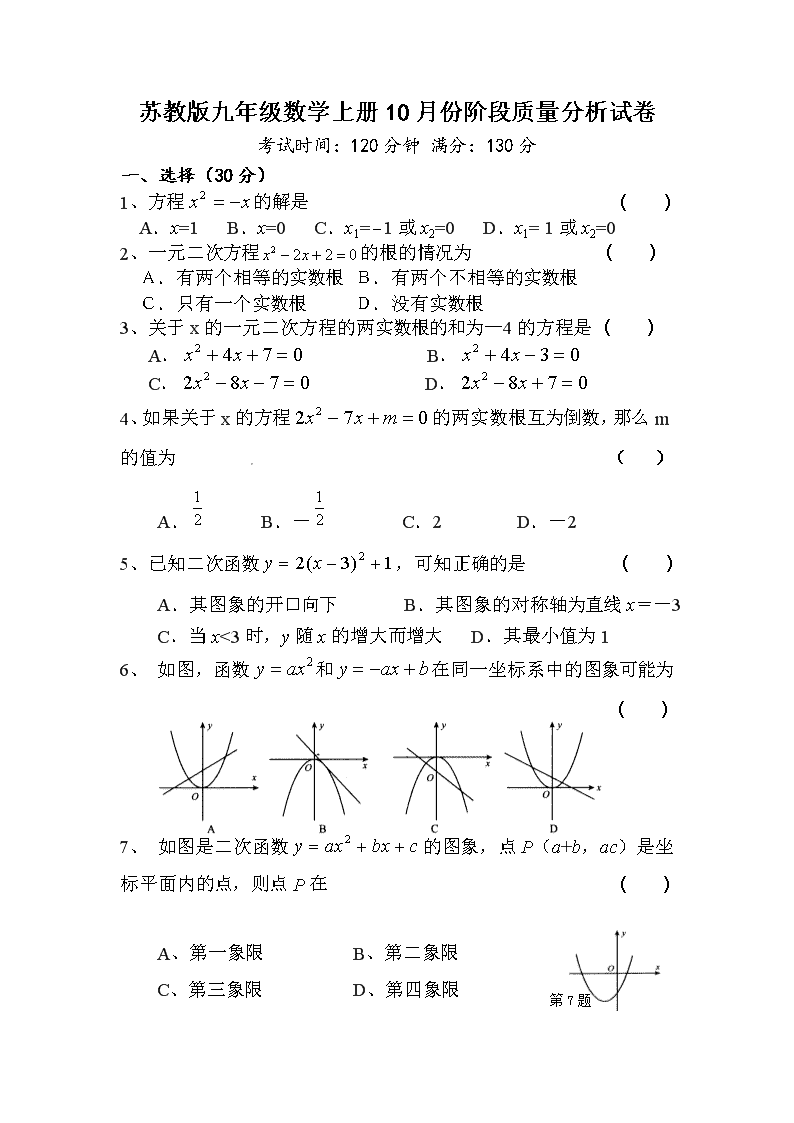
第 7 题 苏教版九年级数学上册 10 月份阶段质量分析试卷 考试时间：120 分钟 满分：130 分 一、选择（30 分） 1、方程 xx 2 的解是 ( ) A．x=1 B．x=0 C．x1= 1 或 x2=0 D．x1= 1 或 x2=0 2、一元二次方程 2 2 2 0x x   的根的情况为 ( ) Ａ．有两个相等的实数根 Ｂ．有两个不相等的实数根 Ｃ．只有一个实数根 Ｄ．没有实数根 3、关于 x 的一元二次方程的两实数根的和为—4 的方程是 ( ) A． 0742  xx B． 0342  xx C． 0782 2  xx D． 0782 2  xx 4、如果关于 x 的方程 072 2  mxx 的两实数根互为倒数，那么 m 的值为 （ ） A． 1 2 B．－ 1 2 C．2 D．－2 5、已知二次函数 1)3(2 2  xy ，可知正确的是 ( ) A．其图象的开口向下 B．其图象的对称轴为直线 x＝－3 C．当 x<3 时，y 随 x 的增大而增大 D．其最小值为 1 6、 如图，函数 2axy  和 baxy  在同一坐标系中的图象可能为 ( ) 7、 如图是二次函数 cbxaxy  2 的图象，点 P（a+b，ac）是坐 标平面内的点，则点 P 在 ( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限 8、已知二次函数 772  xkxy 的图象与 x 轴没有交点，则 k 的取 值范围为 ( ) A、 k﹥－ 4 7 B、 k≥－ 4 7 且 k≠0 C、 k﹤－ 4 7 D、 k﹥－ 4 7 且 k≠0 9、已知二次函数 2 ( 0)y ax bx c a    ，其中a 、b 、c 满足 0a b c   和 9 3 0a b c   ，则该二次函数图像的对称轴是直线 （ ） A. 2x   ；B. 1x   ；C. 2x  ；D. 1x  ； 10、若关于 x 的方程 2 0x px q   的两根同为负数，其中 2 4p q ≥0， 则 ( ) A． p ＞0 且q＞0 B． p ＞0 且q＜0 C． p ＜0 且q＞0 D． p ＜0 且q＜0 二、填空（24 分） 11、已知：方程 24 2 1 0x x   有两实根 1x 、 2x ，则两根之和的值 为 . 12、将抛物线 2 2 1 xy  向上平移 2 个单位，再向右平移 1 个单位后， 得到的抛物线所对应的函数关系式为 ． 13、若关于 x 的方程 0235)1( 22  mmxxm 的常数项为 0，则 m 的值为 . 14、关于 x 的一元二次方程 2 2 0mx mx   有两个相等的实数根， 则 m 的值为 ． 15、三角形两边长是 3 和 4，第三边的长是方程 2 5 6 0x x   的根，则 该三角形周长为 ． 16、抛物线 82 2  bxxy 的顶点在 x 轴的正半轴上，则 b= . 17、二次函数 cbxxy  22 图象的最高点是（－1，－3），则 b= ,c= . 18、已知二次函数 cbxaxy  2 图象如图所 示，下列结论:(1) 0abc , (2) cab  (3) 024  cba (4) 02  ba 其中正确的是 . 三、计算与解答：（76 分） 19、解下列方程：(16 分) ⑴  21 3 1 8 02 x    ⑵ 2 6 6 0x x   ⑶   22 )2(12 yy  ⑷ 12 1 4 4 2   xx 20、（4 分）把函数 22 4 3y x x    用配方法配成顶点式，并写出 它的对称轴和顶点坐标. 21、（5 分）如果方程 2 8 0x x k   的一根是另一根的 3 倍，求k 的 值． 22、（6 分）已知关于 x 的一元二次方程 x2+（m－1）x－2m2+m=0（m 为实数）有两个实数根 x1，x2．（1）当 m 为何值时，x1≠x2； （2）若 x12+x22=2，求 m 的值． 23、（本题 9 分）关于 x 的方程  2 22 4 1 0x a x a     ， (1)a 为何值时，方程的一根为 0？ (2)a 为何值时，两实根互为相反数？ (3)试证明：无论 a 取何值，方程的两实根不可能互为倒数． 24、（6 分）已知关于 x 的一元二次方程 2 212 2 02x kx k    ． ⑴求证：无论k 取什么数，方程总有两个不同的实数根； ⑵方程有两个实数根 1 2,x x 且有 2 1 1 1 22 2 5x kx x x   ，求k 的值． 25、（8 分）如图，开口向上的抛物线与坐标轴分别交于点 A(一 1， 0)、B(3，0)、C(0，一 3)，一次函数的图象与二次函数的图象交于 B、 C 两点．求：(1)一次函数与二次函数的解析式． (2)当自变量 x 为何值时，两函数的函数值都随 x 的增大而增大? (3)当自变量 x 为何值时，一次函数的值大于二 次函数的值? 26、（本题 8 分）二次函数 2y=x +bx+c 的图象经过点（4，3），（3，0）。 （1）求 b、c 的值； （2）求出该二次函数图象的顶点坐标和对称轴； （3）若 1( )A m y， ， 2( 1 )B m y ， 两点都在该函数的图象上，且 1m ， 试比较 1y 与 2y 的大小． 27、（6 分）如图，抛物线 cbxxy  2 与 x 轴交于 A(1，0)、 B(－3，0)两点． (1)求该抛物线的解析式． (2)设抛物线交 y 轴于点 C，在该抛物线的对称轴上是否存在点 Q， 使得△QAC 周长最小?若存在，求出点 Q 的坐标；若不存在，请说明 理由． 28、（8 分）新华商场为迎接家电下乡活动销售某种冰箱，每台进价 为 2500 元，市场调研表明；当销售价定为 2900 元时，平均每天能售 出 8 台；而当销售价每降低 50 元时，平均每天就能多售出 4 台. ⑴商场要想使这种冰箱的销售利润平均每天达到 4800 元，每台冰箱 的定价应为多少元？平均每天可以售出多少台冰箱？ ⑵每天的销售利润 4800 元日是不是最大利润？若不是，试求每台冰 箱的定价为多少元时利润最高，最高是多少？