山东省济南市历下区2020-2021学年度上学期九年级期中考试数学试题 6页

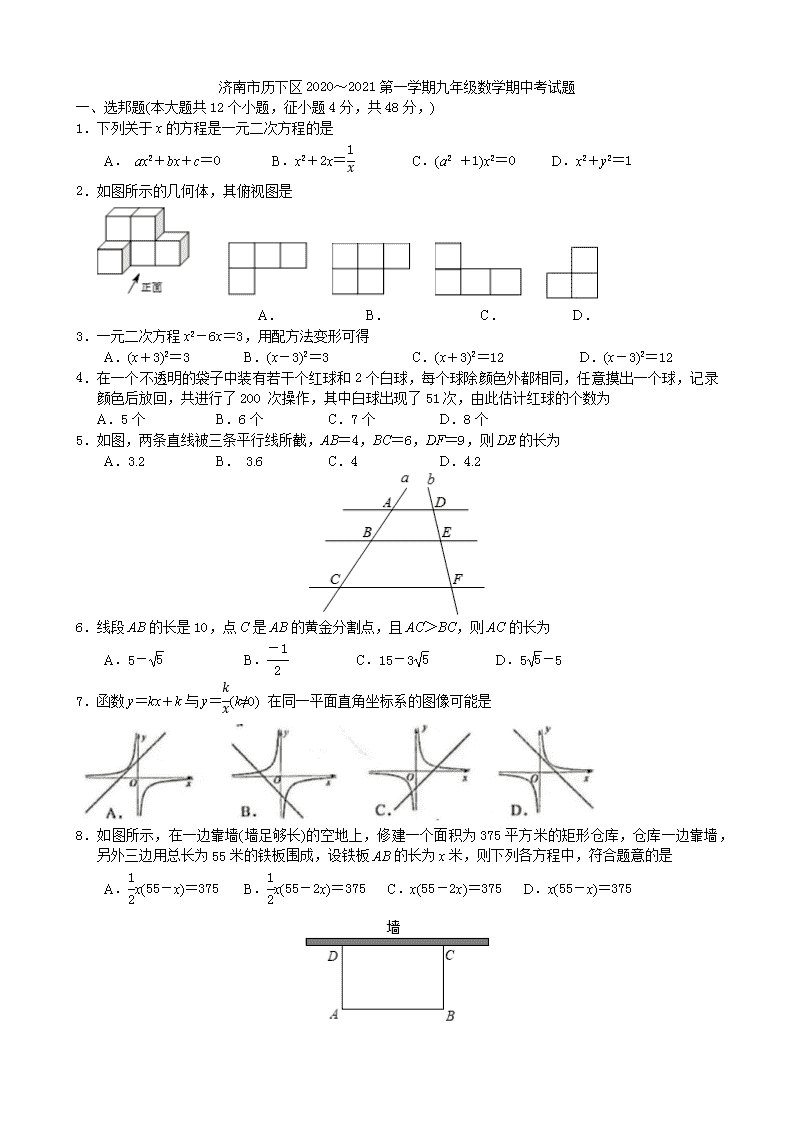
济南市历下区2020～2021第一学期九年级数学期中考试题 一、选邦题(本大题共12个小题，征小题4分，共48分，)‎ ‎1．下列关于x的方程是一元二次方程的是 A． ax2＋bx＋c＝0 B．x2＋2x＝ C．(a2 ＋1)x2＝0 D．x2＋y2＝1‎ ‎2．如图所示的几何体，其俯视图是 ‎ ‎ ‎ A．　　　 B．　　　 C．　　　 D．‎ ‎3．一元二次方程x2－6x＝3，用配方法变形可得 A．(x＋3)2＝3 B．(x－3)2＝3 C．(x＋3)2＝12 D．(x－3)2＝12‎ ‎4．在一个不透明的袋子中装有若干个红球和2个白球，每个球除颜色外都相同，任意摸出一个球，记录颜色后放回，共进行了200 次操作，其中白球出现了51次，由此估计红球的个数为 A．5个 B．6个 C．7个 D．8个 ‎5．如图，两条直线被三条平行线所截，AB＝4，BC＝6，DF＝9，则DE的长为 A．3.2 B． 3.6 C．4 D．4.2‎ ‎6．线段AB的长是10，点C是AB的黄金分割点，且AC＞BC，则AC的长为 A．5－ B． C．15－3 D．5－5‎ ‎7．函数y＝kx＋k与y＝(k≠0) 在同一平面直角坐标系的图像可能是 ‎8．如图所示，在一边靠墙(墙足够长)的空地上，修建一个面积为375平方米的矩形仓库，仓库一边靠墙，另外三边用总长为55米的铁板围成，设铁板AB的长为x米，则下列各方程中，符合题意的是 A．x(55－x)＝375 B．x(55－2x)＝375 C．x(55－2x)＝375 D．x(55－x)＝375‎ ‎9．如图，在△ABC中，点D、E分别是AB和AC边上的点，DE∥BC，AD＝3BD，四边形BDEC的面积是28，则△ABC的面积为 A．61 B．62 C． 63 D．64‎ ‎ ‎ ‎10．已知点A(－1，y1)、B (－2，y2)、C (3，y3)都在反比例函数y＝的图象上，则y1、y2、y3为的关系是 A．y2＞y1＞y3 B．y2＞y3＞y1 C．y3＞y1＞y2 D．y3＞y2＞y1‎ ‎11．如图，EB为驾驶员的盲区，驾驶员的眼睛点P处与地面BE的距离为1.6米，车头FACD近似看成一个矩形，且满足3FD＝2FA，若盲区EB的长度是6米，则车宽FA的长度为( )米 ‎ A．　　　 B．　 　　C．　　 　D．2‎ ‎12．如图，矩形ABCD中，∠BEF＝90°，点E是AD中点，＝，则的值为( )‎ A． B． C． D． ‎ ‎ 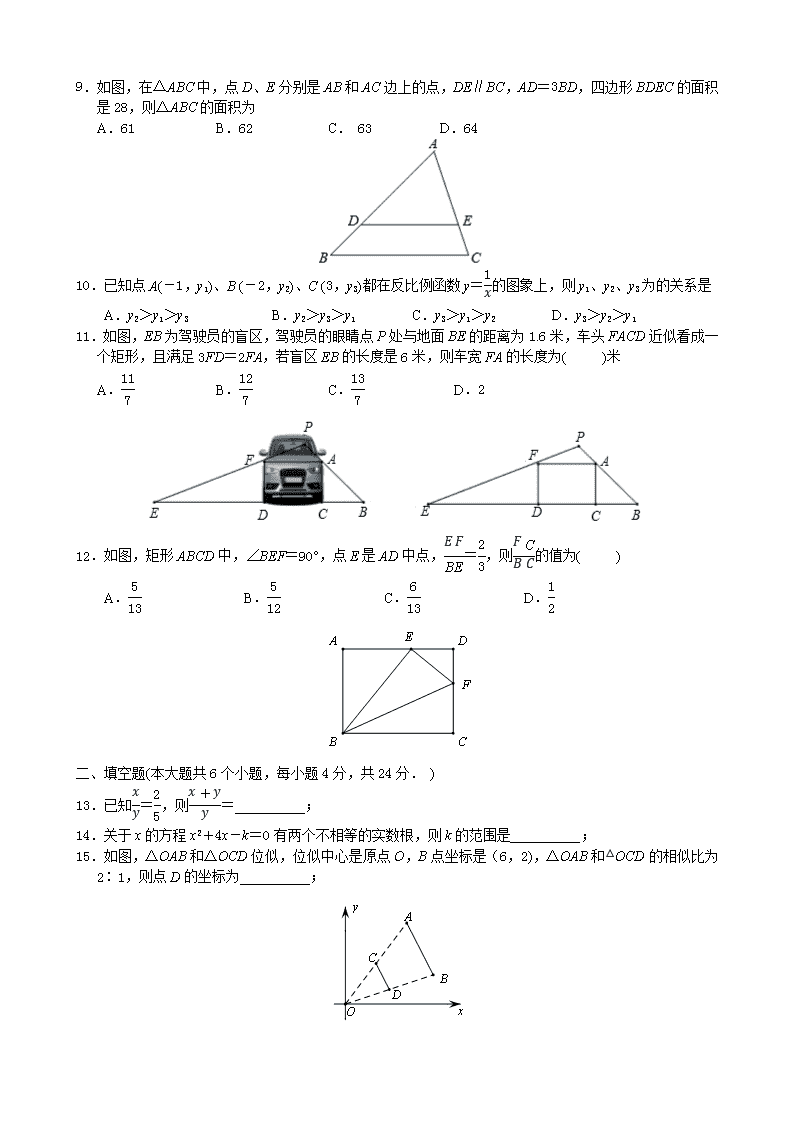二、填空题(本大题共6个小题，每小题4分，共24分． )‎ ‎13．已知＝，则＝__________；‎ ‎14．关于x的方程x2＋4x－k＝0有两个不相等的实数根，则k的范围是__________；‎ ‎15．如图，△OAB和△OCD位似，位似中心是原点O，B点坐标是（6，2)，△OAB和△OCD的相似比为2∶1，则点D的坐标为__________；‎ ‎ ‎ ‎16．如图，小明用相似图形的知识测量旗杆高度，已知小明的眼睛离地面1．5米，他将3米长的标杆竖直放置在身前3米处，此时小明的眼睛、标杆的顶端、旗杆的顾端在一条直线上，通过计算测得旗杆高度为15米，则旗杆和标杆之间距离CE长__________米；‎ ‎ ‎ ‎17．如图，在Rt△ABC中，∠C＝90°，点D是AB的中点，点E是线段AC上的动点，BC＝4，AB＝8，当△ABC和△AED相似时，AE的长为__________；‎ ‎ ‎ ‎18．一次函数y＝kx＋2的图像与反比例函数y＝－的图像的交于点A(1，a)，点O为坐标原点，射线OA交反比例函数y＝的图像于点B，若＝，则m的值为_________．‎ 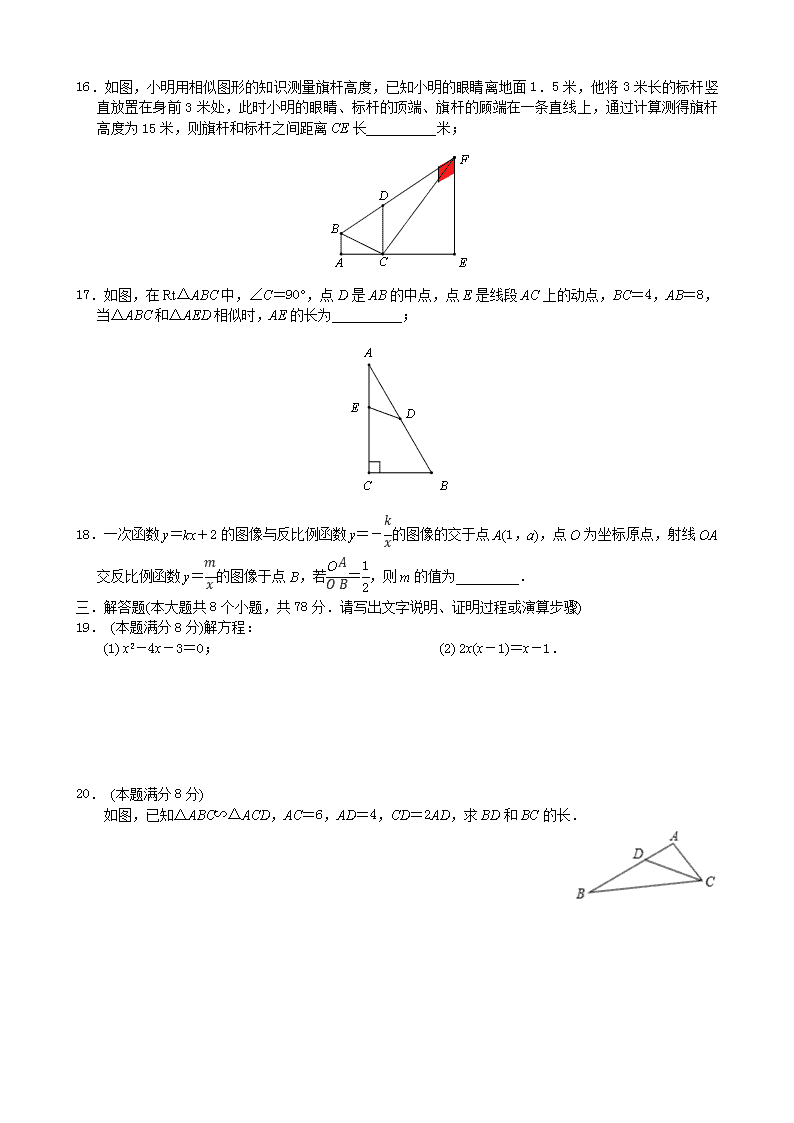三．解答题(本大题共8个小题，共78分．请写出文字说明、证明过程或演算步骤)‎ ‎19． (本题满分8分)解方程：‎ ‎ (1) x2－4x－3＝0； (2) 2x(x－1)＝x－1．‎ ‎20． (本题满分8分)‎ 如图，已知△ABC∽△ACD，AC＝6，AD＝4，CD＝2AD，求BD和BC的长．‎ ‎ ‎ ‎21． (本题满分8分)‎ ‎2020年10月8日，济南轨道交通2号线地质条件最为复杂、盾构施工难度最大的宝长区问顺利贯通一至此， 2号线全部38个单线盾构区间全部贯通．这标志着2号线实现全线”洞通”，距离年底通车目标又近一步．在济南某地铁站，其入口检票处有A、B、C三个闸机．假设乘客通过某地铁站入口时，通过每个闸口的可能性相同，乘客可随机选择一个闸口通过．‎ ‎(1)一名乘客通过此地铁闸口时，选择A闸口通过的概率为__________；‎ ‎(2)当两名乘客通过此地铁闸口时，请用树状图或列表法求两名乘客选择不同闸口通过的概率． ‎ ‎22．(本题满分10分)‎ ‎2020年3月，新冠肺炎疫情在中国已经得到有效控制，但在全球却开始持续蔓延，这是对人类的考验，将对全球造成巨大影响．世界卫生组织提出：如果1人传播10人以上而且被传染的人已经确定为新冠肺炎，那么这个传播者就可以称为”超级传播者”．如果某地区有1人不幸成为新冠肺炎病毒的携带者，假设一个病毒携带者每轮传染的人数相同，经过两轮传染后共有81人成为新冠肺炎病毒的携带者．‎ ‎(1)请判断最初的这名病毒携带者是”超级传播者”吗？求他每轮传染的人数； ‎ ‎(2)若不加以控制传染渠道，经过3轮传染，新冠肺炎病毒的携带者共有多少人？‎ ‎23．(本题满分10分)‎ 如图，矩形ABCD中AB＝2，AD＝4，动点F在线段CD上运动(不与端点重合) ，过点D作AF的垂线，交线段BC于点E．‎ ‎(1)证明：△ADF∽△DCE；‎ ‎(2)当CF＝1时，求EC的长．‎ ‎ ‎ ‎24．(本题满分10分)‎ 定义：若两个一元二次方程有且只有一个相同的实数根，我们就称这两个方程为”同伴方程”．例如x2＝4和(x－2)(x＋3)＝0有且只有一个相同的实数根x＝2，所以这两个方程为”同伴方程”．‎ ‎(1)根据所学定义，下列方程属于”同伴方程”的有__________；(只填写序号即可)‎ ‎①(x－1)2＝9；②x2＋4x＋4＝0；③(x＋4)(x－2)＝0．‎ ‎(2)关于x的一元二次方程x2－2x＝0与x2＋3x＋m－1＝0为”同伴方程”，求m的值；‎ ‎(3)若关于x的一元二次方程ax2＋bx＋c＝0(a≠0)同时满足a＋b＋c＝0和a－b＋c＝0，且与(x＋2)(x－n)＝0互为”同伴方程”，求n的值．‎ ‎25．(本题满分12分)‎ 如图，在平面直角坐标系中，点A(2，m)在正比例函数y＝x(x＞0)的图像上，反比例函数y＝(x＞0)的图像经过点A，点P是x轴正半轴上一动点，过点P作x轴的垂线，与正比例函数y＝x(x＞0)的图像交于点C，点B是线段CP与反比例函数的交点，连接AP、AB．‎ ‎(1)求该反比例函数的表达式；‎ ‎(2)观察图像，请直接写出当x＞0时，x≤的解集；‎ ‎(3)若S△ABP＝1，求B点坐标；‎ ‎(4)点Q是A点右侧双曲线上一动点，是否存在△APQ为以P为直角顶点的等腰直角三角形？若存在，求出点Q坐标；若不存在，请说明理由．‎ ‎ ‎ ‎26．(本题满分12分)‎ 在数学课堂上，小明同学将两个完全相同的直角三角形重合在一起．如图1所示，∠C＝90°，点A与点D重合，点B与点E重合，CA＝kCB．‎ ‎(1)操作发现：当k＝1时，将△DCE饶点C顺时针旋转90°，发现此情况下线段BE和线段AD存在特殊的数量和位置关系：①数量关系：__________；②位置关系：__________；(请直接写出答案)‎ ‎(2)问题产生：当k＝1时，如图2，将△DCE绕点C顺时针旋转α(0°＜α＜90°)，连接BE、AD，在此情况下(1) 中的结论是否还成立呢？请给予你的解释或证明；‎ ‎(3)问题延伸：将(2)中的条件”k＝1”调整为”k＝2”，如图3，其它条件不变：‎ ‎①求此条件下线段BE和线段AD数量关系和位置关系；‎ ‎②在旋转过程中，当E点恰好落在线段AB上时，若BC＝1，求点C到直线AD的距离．‎