九年级上册青岛版数学课件2-2 30°，45°，60°角的三角比 21页

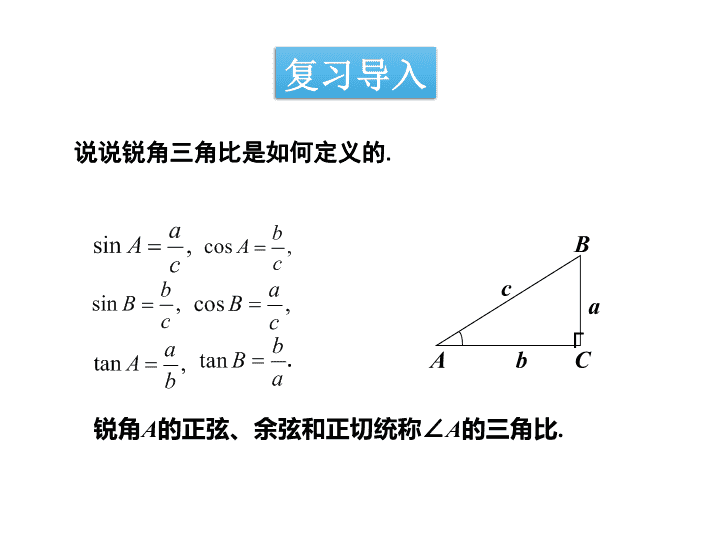
2.2 30°，45°，60°角的三角比 bA B C a ┌ c 锐角A的正弦、余弦和正切统称∠A的三角比. 说说锐角三角比是如何定义的. ,sin c aA  ,cos c bA  ,sin c bB  ,cos c aB  ,tan b aA  ,tan a bB  复习导入 . 1.推导并熟记30°，45°，60°角的三角比. 2.能运用30°，45°，60°角的三角比进行简单计算. 3.能由30°，45°，60°角的三角比求对应的锐角. 学习目标 推进新课 1 特殊角的三角比 探究 30° 60° 45° 45° 1 这两块三角尺的锐角分别等于多少度？ 30° 60° 45° 45° 每块三角尺的三边之间有怎样的特殊关系? 探究 2 a2a 3a a a 2a （设最短的边为a） （1）sin 30°等于多少? cos 30°等于多少? tan 30°呢? （2）45°角的三角比分别是多少？ 探究 3 （3）60°角的三角比分别是多少？ sin α cos α tan α 30° 45° 60° 2 1 2 2 2 3 2 3 2 2 2 1 3 3 3 1 特殊角的三角比表 角α 三角 函数值 三角 比 思考 根据前面的计算填出下表 例1 计算: (1)sin 30°+cos 45°; (2) sin260°+cos260°-tan 45°. 提示: sin260°表示(sin 60°)2, cos260°表示(cos 60°)2,其 余类推. 解: (1)sin 30°+cos 45° 2 2 2 1  12 1 2 3 22           (2) sin260°+cos260°-tan 45° 14 1 4 3  .2 21 .0 例2 一个小孩荡秋千,秋千链子的长度为2.5 m,当秋千向两 边摆动时,摆角恰好为60°,且两边的摆动角度相同,求它摆至 最高位置时与其摆至最低位置时的高度之差（结果精确到 0.01 m）. 将实际问 题数学化 解:如图,根据题意可知, ∠AOD＝ ×60°＝30°,OD＝2.5 m,2 1 ∴OC＝ODcos 30° ＝2.5× 2 3 ≈2.165（m）. ∴AC＝2.5－2.165 ≈0.34（m）. 所以,最高位置与最低位置的高度差约为0.34 m. 练习——牛刀小试 1.(天津中考)cos 60°的值等于(　　) A. B. 1 C. D. 2.(滨州中考)下列运算：sin 30°＝ ， ＝2 ， π0＝π，2-2＝-4，其中运算结果正确的个数为(　　) A．4 B．3 C．2 D．1 3 2 2 1 2 3 2 8 2 D D (1)sin 60°-tan 45°. (2)cos 60°+tan 60°.   .45cos260sin45sin2 23    .45cos260cos30sin2 24 222  3.计算: .8 6-242 22-3132 32122 2-31 ）；（）；（）；（）（  练习——牛刀小试 2 已知特殊三角比求角 通过该表可以方便地知道30°，45°，60°角的 三角比．它的另一个应用：如果已知一个锐角的 三角比，就可以求出这个锐角的度数．例如：若 sin θ＝ ，则锐角θ＝45°.2 2 例3 在Rt△ABC中，∠C＝90°，BC= , AC= ,求 ∠A，∠B的度数. ∵tan A= ∴∠A=30°,∠B=60°. 7 7 3 ,321 BC AC   21 例4 在Rt△ABC中，∠C＝90°，cos A＝ 求∠A， ∠B的度数． 导引：利用特殊角的三角比，查找值所对应的角，再 利用直角三角形两锐角互余的性质求出∠B. 解：∵cos A＝ cos 30°＝ ∴∠A＝30°. ∴∠B＝90°－30°＝60°. 3 ,2 3 ,2 3 ,2 在运用数形结合记忆法或增减规律记忆法记住特 殊角的三角比后，很容易确定∠A的度数，从而 可用两锐角互余的关系计算∠B. 练习——牛刀小试 1.(庆阳中考)在△ABC中，若角A，B满足|cos A－ | ＋(1－tan B)2＝0，则∠C的大小是(　　 ) A．45° B．60° C．75° D．105° 3 2 D 练习——牛刀小试 2.在△ABC中，∠A，∠B都是锐角，且sin A＝ ， cos B＝ ，则△ABC的形状是(　　) A．直角三角形 B．钝角三角形 C．锐角三角形 D．不能确定 1 23 2 B 如图，在Rt△ABC中，∠C＝90°，∠A，∠B， ∠C的对边分别为a，b，c，令∠A＝α. (1)同角三角比之间的关系． ①平方关系：sin2 α＋cos2 α＝1. ②商关系：∵ 且tan α＝ ∴ ＝tan α . 3知识点 锐角三角比之间的关系【拓展】 sin .cos a c    ,b a c b  ,a b sin cos   (2)互余两角的三角比的关系． ①sin A＝cos B，cos A＝sin B． 即任意锐角的正弦值等于它的余角的余弦值， 任意锐角的余弦值等于它的余角的正弦值. ②∵tan A＝ tan B＝ ∴tan A·tan B＝1. 此结论适用于两个角互为余角的情况. ,a b ,b a 课堂小结 30° 45° 60° sin A cos A tan A 1 1 2 1 2 2 2 2 2 3 2 3 2 3 3 3 1.特殊角的三角比: 2.由特殊角的三角比求角度.