中考数学一轮复习知识点+题型专题讲义29 数据的分析（教师版） 18页

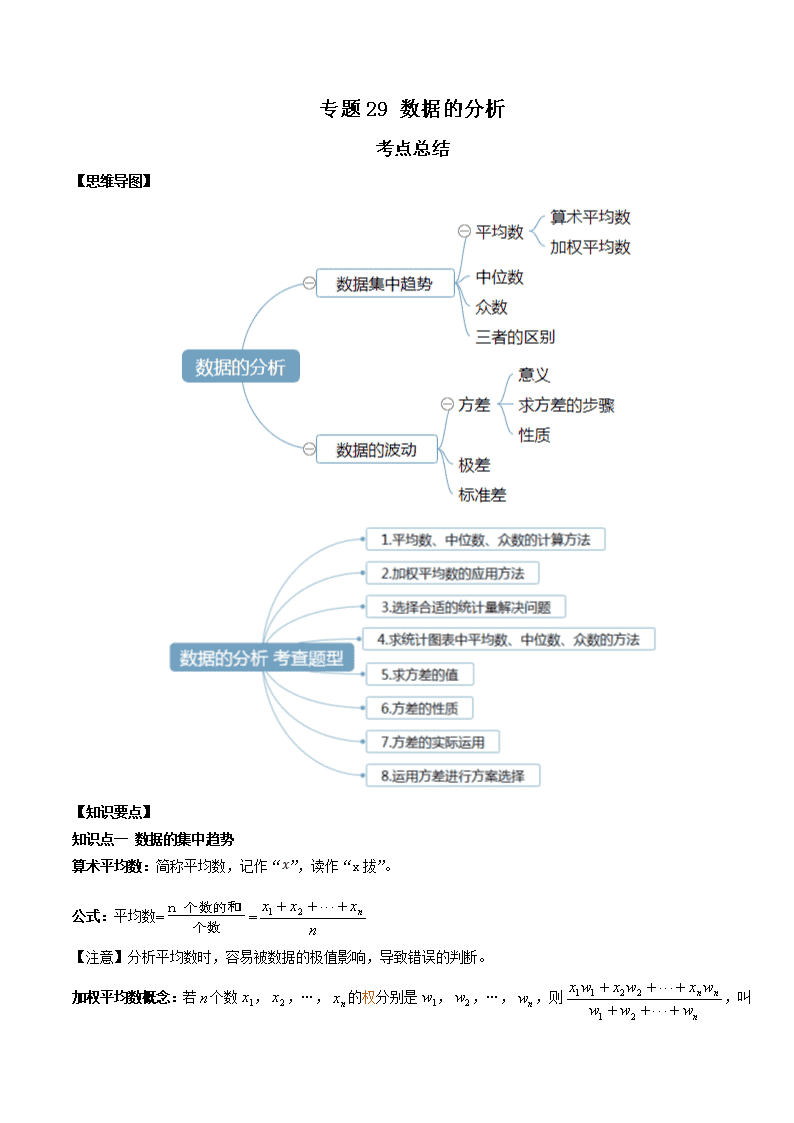
专题 29 数据的分析 考点总结 【思维导图】 【知识要点】 知识点一 数据的集中趋势 算术平均数：简称平均数，记作“ ”，读作“x 拔”。 公式：平均数= n 个数的和 个数 = n xxx n 21 【注意】分析平均数时，容易被数据的极值影响，导致错误的判断。 加权平均数概念：若 n 个数 1x ， 2x ，…， nx 的权分别是 1w ， 2w ，…， nw ，则 n nn www wxwxwx   21 2211 ，叫 做这 n 个数的加权平均数. 【注意】若各数据权重相同，则算术平均数等于加权平均数。 中位数的概念：将一组数据由小到大（或由大到小）的顺序排列，如果数据的个数是奇数，则处于中间位 置的数就是这个数据的中位数，如果数据的个数是偶数，则中间两个数的平均数就是这组数据的中位数。 确定中位数的一般步骤： 第 1 步：排序，由大到小或由小到大。 第 2 步：确定是奇个数据（ ㈠〵 ）或偶个数据（ n 个数和它后一个数 n ㈠ 〵 个数的平均数）。 第 3 步：如果是奇个数据，中间的数据就是中位数。如果是偶数，中位数是中间两个数据的平均数。 众数的概念：一组数据中出现次数最多的数据就是这组数据的众数。 【注意】如果一组数据中有两个数据的频数一样且都是最大，那么这两个数据都是这组数据的众数，所以一组数 据中众数的个数可能不唯一。 众数的意义：当一组数据有较多的重复数据时，众数往往能更好地反映其集中的趋势。 平均数、中位数、众数的区别： 1、平均数的计算要用到所有的数据,它能够充分利用数据提供的信息,在现实生活中较为常用.但它受极端 值的影响较大。 2、 当一组数据中某些数据多次重复出现时,众数往往是人们关心的一个量,众数不受极端值的影响,这是它 的一个优势。但当各个数据的重复次数大致相等时，众数往往没有意义。 3.中位数只需很少的计算,不受极端值的影响,这在有些情况下是一个优点。 【考查题型汇总】 考查题型一 平均数、中位数、众数的计算方法 1．（2019·山东中考模拟）在一次中学生田径运动会上，参加男子跳高的 15 名运动员的成绩如下表所示： 成绩/m 1.50 1.60 1.65 1.70 1.75 1.80 人数 2 3 2 3 4 1 则这些运动员成绩的中位数、众数分别为( ) A．1.70，1.75 B．1.70，1.70 C．1.65，1.75 D．1.65，1.70 【答案】A 【详解】 15 名运动员，按照成绩从低到高排列，第 8 名运动员的成绩是 1.70， 所以中位数是 1.70， 同一成绩运动员最多的是 1.75，共有 4 人， 所以，众数是 1.75． 因此，中位数与众数分别是 1.70，1.75， 故选 A． 2．（2019·四川中考真题）某班七个兴趣小组人数如下：5，6，6， x ，7，8，9，已知这组数据的平均数是 7，则这组数据的中位数是( ) A．6 B．6.5 C．7 D．8 【答案】C 【详解】 ∵5，6，6， x ，7，8，9，这组数据的平均数是 7， ∴  7 7 5 6 6 7 8 9 8x          ， ∴这组数据从小到大排列为：5，6，6，7，8，8，9 ∵这组数据最中间的数为 7， ∴这组数据的中位数是 7． 故选 C． 3．（2019·四川中考真题）某班 40 名同学一周参加体育锻炼时间统计如表所示： 人数（人） 3 17 13 7 时间（小时） 7 8 9 10 那么该班 40 名同学一周参加体育锻炼时间的众数、中位数分别是（ ） A．17，8.5 B．17，9 C．8，9 D．8，8.5 【答案】D 【详解】 解：众数是一组数据中出现次数最多的数，即 8； 由统计表可知，处于 20，21 两个数的平均数就是中位数， ∴这组数据的中位数为 8 9 8.52   ； 故选：D． 4．（2019·湖南中考模拟）据统计，某住宅楼 30 户居民五月份最后一周每天实行垃圾分类的户数依次是：27， 30，29，25，26，28，29，那么这组数据的中位数和众数分别是（ ） A．25 和 30 B．25 和 29 C．28 和 30 D．28 和 29 【答案】D 【详解】对这组数据重新排列顺序得，25，26，27，28，29，29，30， 处于最中间是数是 28， ∴这组数据的中位数是 28， 在这组数据中，29 出现的次数最多， ∴这组数据的众数是 29， 故选 D． 5．（2019·山东中考真题）小明记录了临沂市五月份某周每天的日最高气温(单位： C )，列成如表： 天数(天) 1 2 1 3 最高气温( C ) 22 26 28 29 则这周最高气温的平均值是( ) A． 26.25 C B． 27 C C． 28 C D． 29 C 【答案】B 【详解】 这周最高气温的平均值为    1 1 22 2 26 1 28 3 29 277 C         ； 故选：B． 6．（2019·山东中考真题）在光明中学组织的全校师生迎“五四”诗词大赛中，来自不同年级的 25 名参赛同学 的得分情况如图所示．这些成绩的中位数和众数分别是（ ） A．96 分，98 分 B．97 分，98 分 C．98 分，96 分 D．97 分，96 分 【答案】A 【详解】 98 出现了 9 次，出现次数最多，所以数据的众数为 98 分； 共有 25 个数，最中间的数为第 13 个数，是 96，所以数据的中位数为 96 分． 故选 A． 考查题型二 加权平均数的应用方法 1．（2016·内蒙古中考真题）从一组数据中取出 a 个 x1，b 个 x2，c 个 x3，组成一个样本，那么这个样本的 平均数是（ ） A． 〵㈠㈠ B． 〵㈠㈠ ㈠㈠ C． 〵㈠㈠ D． ㈠㈠ 【答案】B 【详解】 由题意知，a 个 x1 的和为 ax1，b 个 x2 的和为 bx2，c 个 x3 的和为 cx3，数据总共有 a+b+c 个，所以这个样本 的平均数= 〵㈠㈠ ㈠㈠ ，故选 B． 2．（2019·双柏县雨龙中学中考模拟）某公司招聘考试分笔试和面试，其中笔试按 60%，面试按 40%计算加 权平均数作为总成绩，小红笔试成绩为 90 分，面试成绩为 80 分，那么小红的总成绩为( ) A．80 分 B．85 分 C．86 分 D．90 分 【答案】C 【详解】 解：根据题意得： 小红的总成绩为：90×60%+80×40%＝86(分)， 故选：C． 3．（2019·湖北中考真题）某中学规定学生的学期体育成绩满分为 100 分，其中早锻炼及体育课外活动占 20%， 期中考试成绩占 30%，期末考试成绩占 50%.小桐的三项成绩（百分制）依次为 95，90，85.则小桐这学期的 体育成绩是（ ） A．88.5 B．86.5 C．90 D．90.5 【答案】A 【详解】 根据题意得：95×20%+90×30%+85×50%=88.5（分）， 即小彤这学期的体育成绩为 88.5 分． 故选 A． 4．（2019·河南郑州实验外国语中学中考模拟）在某中学理科竞赛中，张敏同学的数学、物理、化学得分(单 位：分)分别为 84，88，92，若依次按照 4：3：3 的比例确定理科成绩，则张敏的成绩是( ) A．84 分 B．87.6 分 C．88 分 D．88.5 分 【答案】B 【详解】 解： 84 4 88 3 92 3 87.64 3 3        （分）. 5．（2019·福建中考模拟）小明是“大三”学生，按照学校积分规则，如果他的学期数学成绩达到 95 分，就能 获得“保研”资格．在满分为 100 分的期中、期末两次数学考试中，他的两次成绩的平均分为 90 分．如果按 期中数学成绩占 30%，期末数学成绩占 70%计算学期数学成绩，那么小明能获得“保研”资格吗？请你运用 所学知识帮他做出判断，并说明理由． 【答案】见解析 【详解】 按期中数学成绩占 30%，期末数学成绩占 70%计算学期数学成绩， 可得期末数学成绩 100 分，期中数学成绩 80 分的成绩最高， 80×30%+100×70%＝24+70＝94（分） ∵94 分＜95 分， ∴小明不能获得“保研”资格． 6．（2015·内蒙古中考真题）学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大 赛，学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试，他们各自的成绩（百 分制）如表： 选手 表达能力 阅读理解 综合素质 汉字听写 甲 85 78 85 73 乙 73 80 82 83 （1）由表中成绩已算得甲的平均成绩为 80.25，请计算乙的平均成绩，从他们的这一成绩看，应选派谁； （2）如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们 2、1、3 和 4 的权，请分别计算两名选 手的平均成绩，从他们的这一成绩看，应选派谁． 【答案】(1)甲；(2)乙. （1） x乙 =（73+80+82+83）÷4=79.5， ∵80.25＞79.5， ∴应选派甲； （2） x甲 =（85×2+78×1+85×3+73×4）÷（2+1+3+4）=79.5， x乙 =（73×2+80×1+82×3+83×4）÷（2+1+3+4）=80.4， ∵79.5＜80.4， ∴应选派乙． 考查题型三 选择合适的统计量解决问题 1．（2019·浙江中考真题）车间有 20 名工人，某天他们生产的零件个数统计如下表． 车间 20 名工人某一天生产的零件个数统计表 生产零件的个数（个） 9 10 11 12 13 15 16 19 20 工人人数（人） 1 1 6 4 2 2 2 1 1 （1）求这一天 20 名工人生产零件的平均个数； （2）为了提高大多数工人的积极性，管理者准备实行“每天定额生产，超产有奖”的措施．如果你是管理者， 从平均数、中位数、众数的角度进行分析，你将如何确定这个“定额”？ 【答案】（1）这一天 20 名工人生产零件的平均个数为 13 个；（2）定额为 11 个时，有利于提高大多数工人 的积极性. 【详解】 解：（1）  1 9 1 10 1 11 6 12 4 13 2 15 2 16 2 19 1 20 1 =1320x                   （个） 答：这一天 20 名工人生产零件的平均个数为 13 个. （2）中位数为 12 个，众数为 11 个. 当定额为 13 个时，有 8 个达标，6 人获奖，不利于提高工人的积极性. 当定额为 12 个时，有 12 个达标，8 人获奖，不利于提高大多数工人的积极性. 当定额为 11 个时，有 18 个达标，12 人获奖，有利于提高大多数工人的积极性. ∴当定额为 11 个时，有利于提高大多数工人的积极性. 2（2019·云南中考真题）某公司销售部有营业员 15 人，该公司为了调动营业员的积极性，决定实行目标管 理，根据目标完成的情况对营业员进行适当的奖励，为了确定一个适当的月销售目标，公司有关部门统计 了这 15 人某月的销售量，如下表所示： 月销售量/件数 1770 480 220 180 120 90 人数 1 1 3 3 3 4 (1)直接写出这 15 名营业员该月销售量数据的平均数、中位数、众数； (2)如果想让一半左右的营业员都能达到月销售目标，你认为(1)中的平均数、中位数、众数中，哪个最适合 作为月销售目标？请说明理由. 【答案】(1)平均数为 278，中位数为 180，众数为 90；(2)中位数最适合作为月销售目标，理由见解析. 【详解】 (1)这 15 名销售人员该月销售量数据的平均数为 1770 480 220 3 180 3 120 3 90 4 15          =278， 排序后位于中间位置的数为 180，故中位数 180， 数据 90 出现了 4 次，出现次数最多，故众数为 90； (2)中位数最适合作为月销售目标.理由如下： 在这 15 人中，月销售额不低于 278(平均数)件的有 2 人，月销售额不低于 180(中位数)件的有 8 人，月销售 额不低于 90(众数)件的有 15 人. 所以，如果想让一半左右的营销人员都能够达到月销售目标，(1)中的平均数、中位数、众数中，中位数最 适合作为月销售目标. 3．（2019·贵阳市第三中学中考模拟）为了解某小区居民使用共享单车次数的情况，某研究小组随机采访该 小区的 10 位居民，得到这 10 位居民一周内使用共享单车的次数统计如下： 使用次数 0 5 10 15 20 人数 1 1 4 3 1 （1）这 10 位居民一周内使用共享单车次数的中位数是 次，众数是 次，平均数是 次． （2）若小明同学把数据“20”看成了“30”，那么中位数，众数和平均数中不受影响的是 ．（填“中位数”， “众数”或“平均数”） （3）若该小区有 200 名居民，试估计该小区居民一周内使用共享单车的总次数． 【答案】(1)10、10、11；(2)中位数和众数;(3)2200 次 【详解】 解：（1）这 10 位居民一周内使用共享单车次数的中位数是10 10 2  ＝10（次）， 众数为 10 次， 平均数为 0 1 5 1 10 4 15 3 20 1 10          ＝11（次）， 故答案为：10、10、11； （2）把数据“20”看成了“30”，那么中位数，众数和平均数中不受影响的是中位数和众数， 故答案为：中位数和众数． （3）估计该小区居民一周内使用共享单车的总次数为 200×11＝2200 次． 4．（2018·湖北中考真题）为了参加“荆州市中小学生首届诗词大会”，某校八年级的两班学生进行了预选， 其中班上前 5 名学生的成绩（百分制）分别为：八（1）班 86，85，77，92，85；八（2）班 79，85，92， 85，89．通过数据分析，列表如下： 班级 平均分 中位数 众数 方差 八（1） 85 b c 22.8 八（2） a 85 85 19.2 （1）直接写出表中 a，b，c 的值； （2）根据以上数据分析，你认为哪个班前 5 名同学的成绩较好？说明理由． 【答案】（1）a=86，b=85，c=85；（2）八（2）班前 5 名同学的成绩较好，理由见解析. 【详解】（1）a= 78 85 92 85 89 5     ， 将八（1）的成绩排序 77、85、85、86、92， 可知中位数是 85，众数是 85， 所以 b=85，c=85； （2）∵22.8＞19.2， ∴八（2）班前 5 名同学的成绩较好. 考查题型四 求统计图表中平均数、中位数、众数的方法 1．（2019·河南中考模拟）某工厂生产部门为了解本部门工人的生产能力情况，进行了抽样调查．该部门随 机抽取了 30 名工人某天每人加工零件的个数，数据如下： 20 21 19 16 27 18 31 29 21 22 25 20 19 22 35 33 19 17 18 29 18 35 22 15 18 18 31 31 19 22 整理上面数据，得到条形统计图： 样本数据的平均数、众数、中位数如下表所示： 统计量 平均数 众数 中位数 数值 23 m 21 根据以上信息，解答下列问题： （1）上表中众数 m 的值为 ； （2）为调动工人的积极性，该部门根据工人每天加工零件的个数制定了奖励标准，凡达到或超过这个标准 的工人将获得奖励．如果想让一半左右的工人能获奖，应根据 来确定奖励标准比较合适．（填“平均 数”、“众数”或“中位数”） （3）该部门规定：每天加工零件的个数达到或超过 25 个的工人为生产能手．若该部门有 300 名工人，试 估计该部门生产能手的人数． 【答案】(1)18；（2）中位数；（3）100 名. 【详解】（1）由图可得， 众数 m 的值为 18， 故答案为：18； （2）由题意可得， 如果想让一半左右的工人能获奖，应根据中位数来确定奖励标准比较合适， 故答案为：中位数； （3）300×1 1 2 3 1 2 30      =100（名）， 答：该部门生产能手有 100 名工人． 2．（2010·河北中考真题）甲、乙两校参加区教育局举办的学生英语口语竞赛，两校参赛人数相等.比赛结束 后，发现学生成绩分别为 7 分、8 分、9 分、10 分（满分为 10 分）.依据统计数据绘制了如图所示的尚不完 整的统计图表. 甲校成绩统计表 分数 7 分 8 分 9 分 10 分 人数 11 0 8 （1）在图①中，“7 分”所在扇形的圆心角等于______  ； （2）请你将②的统计图补充完整； （3）经计算，乙校的平均分是 8.3 分，中位数是 8 分，请写出甲校的平均分、中位数；并从平均分和中位 数的角度分析哪个学校成绩较好； （4）如果该教育局要组织 8 人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参 赛选手，请你分析，应选哪所学校？ 【答案】（1）144°；（2）乙校得 8 分的学生的人数为 3 人，据此可将图②的统计图补充完整如图③见解析； （3）从平均分和中位数的角度分析乙校成绩较好；（4）应选甲校. 【详解】 (1)由图①知“10 分”的所在扇形的圆心角是 90 度，由图②知 10 分的有 5 人，所以乙校参加英语竞赛的人数 为：5÷ 90 360 =20(人)， 所以“7 分”所在扇形的圆心角=360°× 8 20 =144°， 故答案为：144； (2)乙校得 8 分的学生的人数为 20 8 4 5 3    (人)， 补全统计图如图所示： (3)由(1)知甲校参加英语口语竞赛的学生人数也是 20 人， 故甲校得 9 分的学生有 20 11 8 1   (人)， 所以甲校的平均分为： 7 11 9 10 8 8.320      (分)，中位数为 7 分， 而乙校的平均数为 8.3 分，中位数为 8 分， 因为两校的平均数相同，但甲校的中位数要低于乙校，所以从平均分和中位数的角度分析乙校成绩较好； (4)选 8 名学生参加市级口语团体赛，甲校得 10 分的有 8 人，而乙校得 10 分的只有 5 人，所以应选甲校. 知识点二 数据的波动 方差的概念：在一组数据 1x ， 2x ，…， nx 中，各个数据与平均数的差的平方的平均数叫做这组数据的方差， 记作 2s .计算公式是：       22 2 2 1 2 1 xxxxxxns n  求一组数据方差的步骤：先平均、再做差、然后平方、最后再求平均数。 方差的意义：方差是用来衡量数据在平均数附近波动大小的量，方差（ 2s ）越大，数据的波动性越大，方 差越小，数据的波动性越小. 【性质】 ①当一组数据同时加上一个数 a 时，其平均数、中位数、众数也增加 a ,而其方差不变； ②当一组数据扩大 k 倍时，其平均数、中位数和众数也扩大 k 倍，其方差扩大 2k 倍. 标准差的概念：方差的算术平方根.       n xxxxxxs n 22 2 2 1  极差的概念：一组数据中最大值减去最小值的差叫做极差。 极差的意义：反映了这组数据的变化范围。 【考查题型汇总】 考查题型五 求方差的值 1．（2019·辽宁中考模拟）如果一组数据 6、7、x、9、5 的平均数是 2x，那么这组数据的方差为（ ） A．4 B．3 C．2 D．1 【答案】A 【解析】 根据题意，得： 6 7 9 5 5 x    =2x 解得：x=3， 则这组数据为 6、7、3、9、5，其平均数是 6， 所以这组数据的方差为 1 5 [（6﹣6）2+（7﹣6）2+（3﹣6）2+（9﹣6）2+（5﹣6）2]=4， 故选 A． 考查题型六 方差的性质 1．（2018·湖南中考真题）若一组数据 1a , 2a , 3a 的平均数为 4，方差为 3，那么数据 1 2a  , 2 2a  , 3 2a  的 平均数和方差分别是（ ） A．4, 3 B．6, 3 C．3, 4 D．6 5 【答案】B 【解析】 详解：∵数据 a1，a2，a3 的平均数为 4， ∴ 1 3 （a1+a2+a3）=4， ∴ 1 3 （a1+2+a2+2+a3+2）= 1 3 （a1+a2+a3）+2=4+2=6， ∴数据 a1+2，a2+2，a3+2 的平均数是 6； ∵数据 a1，a2，a3 的方差为 3， ∴ 1 3 [（a1-4）2+（a2-4）2+（a3-4）2]=3， ∴a1+2，a2+2，a3+2 的方差为： 1 3 [（a1+2-6）2+（a2+2-6）2+（a3+2-6）2] = 1 3 [（a1-4）2+（a2-4）2+（a3-4）2] =3． 故选：B． 2．（2019·河北中考模拟）若一组数据 x1+1，x2+1，…，xn+1 的平均数为 17，方差为 2，则另一组数据 x1+2， x2+2，…，xn+2 的平均数和方差分别为（ ） A．17，2 B．18，2 C．17，3 D．18，3 【答案】B 【详解】 ∵x1+1，x2+1，…，xn+1 的平均数为 17，方差为 2， ∴x1+2，x2+2，…，xn+2 的平均数和方差分别为 18，2. 故选 B. 3．（2019·山东中考模拟）如果数据 x1，x2，…，xn 的方差是 3，则另一组数据 2x1，2x2，…，2xn 的方差是 （ ） A．3 B．6 C．12 D．5 【答案】C 【详解】根据题意，数据 x1，x2，…，xn 的平均数设为 a， 则数据 2x1，2x2，…，2xn 的平均数为 2a， 根据方差公式：        2 2 2 22 1 2 3 1 nS x a x a x a x an            =3， 则        2 2 2 22 1 2 3 1 2 2 2 2 2 2 2 2nS x a x a x a x an            =        2 2 2 2 1 2 3 1 4 4 4 4 nx a x a x a x an           =4×        2 2 2 2 1 2 3 1 nx a x a x a x an           =4×3 =12， 考查题型七 方差的实际运用 1．（2018·河北中考真题）为考察甲、乙、丙、丁四种小麦的长势，在同一时期分别从中随机抽取部分麦苗， 获得苗高（单位：cm）的平均数与方差为： x甲 = x丙 =13， x乙 = x丁 =15：s 甲 2=s 丁 2=3.6，s 乙 2=s 丙 2=6.3．则 麦苗又高又整齐的是（ ） A．甲 B．乙 C．丙 D．丁 【答案】D 【详解】 ∵ x乙 = x丁 ＞ x甲 = x丙 ， ∴乙、丁的麦苗比甲、丙要高， ∵s 甲 2=s 丁 2＜s 乙 2=s 丙 2， ∴甲、丁麦苗的长势比乙、丙的长势整齐， 综上，麦苗又高又整齐的是丁， 故选 D． 2．（2019·甘肃中考模拟）如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差： 甲 乙 丙 丁 平均数（cm） 185 180 185 180 方差 3.6 3.6 7.4 8.1 根据表数据，从中选择一名成绩好且发挥稳定的参加比赛，应该选择（ ） A．甲 B．乙 C．丙 D．丁 【答案】A 【详解】 ∵ x甲 = x丙 > x乙 = x丁 ， ∴从甲和丙中选择一人参加比赛， ∵ 2S甲 = 2S乙 < 2S丙 < 2S丁 ， ∴选择甲参赛， 故选 A． 3．（2019·辽宁中考真题）甲、乙、丙、丁四人进行射箭测试，每人 10 次射箭成绩的平均成绩都相同，方差 分别是 S 甲 2=0.65，S 乙 2=0.55，S 丙 2=0.50，S 丁 2=0.45，则射箭成绩最稳定的是（ ） A．甲 B．乙 C．丙 D．丁 【答案】D 【详解】 ∵射箭成绩的平均成绩都相同,方差分别是 S 甲 2=0.65，S 乙 2=0.55，S 丙 2=0.50，S 丁 2=0.45， ∴S2 甲>S2 乙>S2 丙>S2 丁， ∴射箭成绩最稳定的是丁； 故选 D. 4．（2019·浙江中考真题）去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了 10 棵，每棵产量 的平均数 x （单位：千克）及方差 2S （单位：千克 2 ）如下表所示： 甲 乙 丙 丁 x 24 24 23 20 2S 2.1 1.9 2 1.9 今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植，应选的品种是（ ） A．甲 B．乙 C．丙 D．丁 【答案】B 【详解】 因为甲组、乙组的平均数丙组比丁组大， 而乙组的方差比甲组的小， 所以乙组的产量比较稳定， 所以乙组的产量既高又稳定， 故选 B． 5．（2017·广东中考模拟）甲、乙、丙、丁四位同学五次数学测验成绩统计如表．如果从这四位同学中，选 出一位成绩较好且状态稳定的同学参加全国数学联赛，那么应选（ ） 甲 乙 丙 丁 平均数 80 85 85 80 方 差 42 42 54 59 A．甲 B．乙 C．丙 D．丁 【答案】B 【解析】 乙和丙的平均数较高，甲和乙的方差较小，则选择乙比较合适．故选 B. 考查题型八 运用方差进行方案选择 1．（2018·山东中考模拟）我市某中学举行“中国梦•校园好声音”歌手大赛，高、初中部根据初赛成绩，各选 出 5 名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的 5 名选手的决赛成绩如图所示． （1）根据图示填写下表； 平均数（分） 中位数（分） 众数（分） 初中部 85 高中部 85 100 （2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好； （3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定． 【答案】（1） 平均数（分） 中位数（分） 众数（分） 初中部 85 85 85 高中部 85 80 100 （2）初中部成绩好些（3）初中代表队选手成绩较为稳定 【解析】 解：（1）填表如下： 平均数（分） 中位数（分） 众数（分） 初中部 85 85 85 高中部 85 8 100 （2）初中部成绩好些． ∵两个队的平均数都相同，初中部的中位数高， ∴在平均数相同的情况下中位数高的初中部成绩好些． （3）∵ ， 2 2 2 2 2 2S 70 85 100 85 100 85 75 85 80 85 160          高中队 （ ） （ ） （ ） （ ） （ ） ， ∴ 2S初中队 ＜ 2S高中队 ，因此，初中代表队选手成绩较为稳定． 2．（2019·如皋市实验初中中考模拟）某校七年级两个班，各选派 10 名学生参加学校举行的“美丽绍兴乡土 风情知识”大赛预赛，各参赛选手的成绩如下： 七(1)班：88，91，92，93，93，93，94，98，98，100； 七(2)班：89，93，93，93，95，96，96，98，98，99． 通过整理，得到数据分析表如下： 班级 最高分 平均分 中位数 众数 方差 八(1)班 100 m 93 93 12 八(2)班 99 95 n 93 8.4 (1)求表中 m、n 的值； (2)依据数据分析表，请您写出两条支持七(2)班成绩好的理由． 【答案】（1）八（1）班的平均分 94；八（2）班的中位数 95.5；（2）支持八（2）班成绩好．理由见解析. 【详解】 （1）八（1）班的平均分 m＝ 1 10 ×（88+91+92+93+93+93+94+98+98+100）＝94； 八（2）班的中位数 n＝ 95 96 2  ＝95.5； （2）八（2）班的平均分高于八（1）班；八（2）班的成绩集中在中上游，故支持八（2）班成绩好．