2020学年度九年级数学上册 第4章 图形的相似单元测试卷 （新版）北师大版 7页

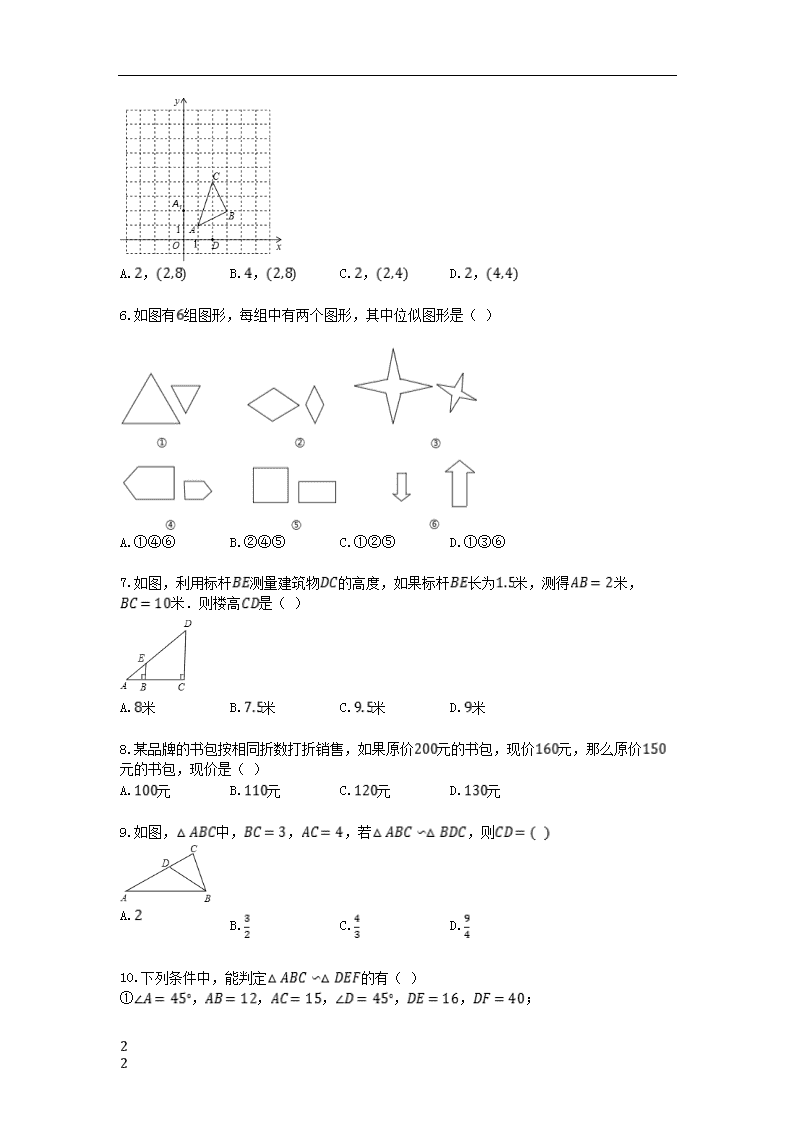
第四章相似三角形 考试总分： 120 分 考试时间： 120 分钟 一、选择题（共 10 小题 ，每小题 3 分 ，共 30 分 ）‎ ‎ ‎ ‎1.已知，则下列比例式成立的是（ ）‎ A.‎ B.‎ C.‎ D.‎ ‎ ‎ ‎2.已知，下列说法中，错误的是（ ）‎ A.‎ B.‎ C.‎ D.‎ ‎ ‎ ‎3.数学课外活动小组为测量学校旗杆的高度，在同一时刻，测得一标杆的高为米，其影长为米，此时旗杆的影长为米，则旗杆的实际高度为（ ）‎ A.米 B.米 C.米 D.米 ‎ ‎ ‎4.若线段是和的比例中项，则的值为（ ）‎ A.‎ B.‎ C.‎ D.‎ ‎ ‎ ‎5.如图，以点为位似中心，作的一个位似三角形，，，的对应点分别为，，，与的比值为，若两个三角形的顶点及点均在如图所示的格点上，则的值和点的坐标分别为（ ）‎ 7‎ A.，‎ B.，‎ C.，‎ D.，‎ ‎ ‎ ‎6.如图有组图形，每组中有两个图形，其中位似图形是（ ） ‎ A.①④⑥‎ B.②④⑤‎ C.①②⑤‎ D.①③⑥‎ ‎ ‎ ‎7.如图，利用标杆测量建筑物的高度，如果标杆长为米，测得米，米．则楼高是（ ）‎ A.米 B.米 C.米 D.米 ‎ ‎ ‎8.某品牌的书包按相同折数打折销售，如果原价元的书包，现价元，那么原价元的书包，现价是（ ）‎ A.元 B.元 C.元 D.元 ‎ ‎ ‎9.如图，中，，，若，则 ‎ A.‎ B.‎ C.‎ D.‎ ‎ ‎ ‎10.下列条件中，能判定的有（ ） ①，，，，，‎ 7‎ ‎； ②，，，，，； ③，，，，，．‎ A.个 B.个 C.个 D.个 二、填空题（共 10 小题 ，每小题 3 分 ，共 30 分 ）‎ ‎ ‎ ‎11.请指出图中从图到图的变换是________变换．‎ ‎ ‎ ‎12.线段是线段，的比例中项，且，，则________．‎ ‎ ‎ ‎13.如图，在中，，，则图中的相似三角形共有________对．‎ ‎ ‎ ‎14.如图，在中，，，，，则________．‎ ‎ ‎ ‎15.把一个矩形的各边都扩大倍，其面积扩大________倍．‎ ‎ ‎ ‎16.如图，，，，则________．‎ ‎ ‎ ‎17.如图，在中，、、分别是、、上的点，且，，，长为，则的长为________．‎ ‎ ‎ ‎18.两个相似三角形的周长比是，那么这两个三角形的相似比是________．‎ ‎ ‎ ‎19.如图，已知中的，则放大镜下中________度．‎ 7‎ ‎ ‎ ‎20.如图，路灯（点）距地面米，身高米的小明从距路灯的底部（点）米的点，沿所在的直线行走米到点时，身影的长度变短了________米．‎ 三、解答题（共 6 小题 ，每小题 10 分 ，共 60 分 ）‎ ‎ ‎ ‎21.如图，在和中，已知，，求证：．‎ ‎ ‎ ‎22.已知的三边长分别为，，，两边的长分别为，，且与相似，求的第三边．‎ ‎ ‎ ‎23.如图，在中，、两点分别在、两边上，，，，，求的长．‎ ‎ ‎ ‎24.如图，将一副三角板按图叠放，则与相似吗？请说明理由．‎ ‎ ‎ ‎25.一位同学想利用树影测树高．在某一时刻测得的竹竿的影长为，但当他马上测树影时，发现影子不全落在地上，一部分落在了附近的一幢高楼上（如图）．于是他只得测出了留在墙上的影长为，以及地面部分上的影长为．请你帮他算一下树高到底有多高．‎ 7‎ ‎ ‎ ‎26.阅读下面材料： 如图，在中，是边上的点（不与点、重合），连结．‎ 当点是边上的中点时，________；‎ 如图，在中，点是线段上一点（不与点、重合），且，连结、，求的值（用含的代数式表示）；‎ 如图，是线段上一点（不与点、重合），连结并延长交于点，连结并延长交于点，补全图形并直接写出的值． ‎ 答案 ‎1.B ‎2.C ‎3.B ‎4.C ‎5.A ‎6.A ‎7.D ‎8.C ‎9.D ‎10.C ‎11.相似 ‎12.‎ ‎13.‎ ‎14.‎ ‎15.‎ ‎16.‎ ‎17.‎ ‎18.‎ ‎19.‎ ‎20.‎ ‎21.证明：如图，∵， ∴，即． 又∵， ∴．‎ ‎22.解：∵的三边长分别为，，，两边的长分别为，，且与 7‎ 相似， ∴相似比为：， ∴， 解得：， ∴的第三边为．‎ ‎23.解：在和中， ∵， ∴ ∴ ∴‎ ‎24.解：． ∵， ∴， ∴， ∴．‎ ‎25.解：如图： 设树高为米， 过作于， 则有， ， 解得． 故树高有．‎ ‎26.；如图，作于，作于， ∴． ∴， ∴． ∵； ∴‎ 7‎ ‎， ∵， ∴．． 理由：∵， 同理：，， ∴．‎ 7‎