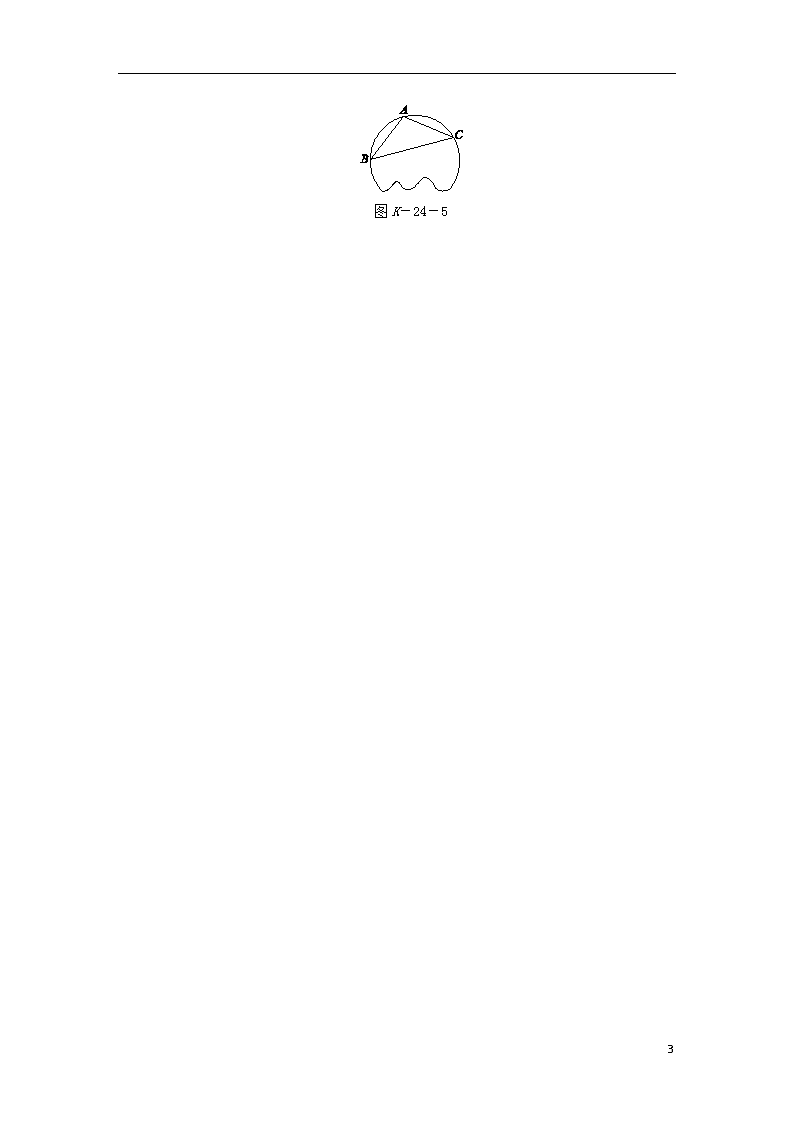2020九年级数学下册 第三章 圆 9页

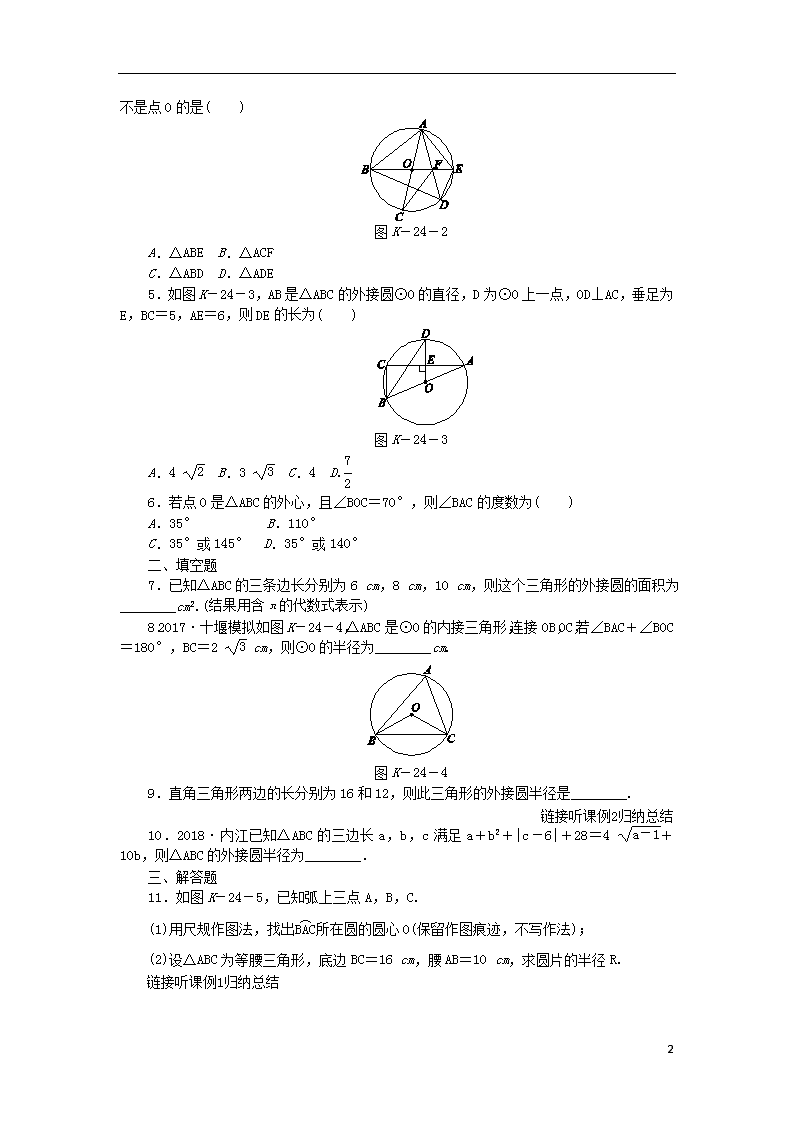
课时作业(二十四)‎ ‎[第三章　5　确定圆的条件]‎ 一、选择题 ‎1．下列四个命题中正确的有(　　)‎ ‎①经过三角形顶点的圆是三角形的外接圆；②任何一个三角形一定有一个外接圆，并且只有一个外接圆；③任何一个圆一定有一个内接三角形，并且只有一个内接三角形；④三角形的外心是三角形三条边的垂直平分线的交点．‎ A．1个 B．2个 C．3个 D．4个 ‎2．三角形的外心具有的性质是(　　)‎ A．到三个顶点的距离相等 B．到三条边的距离相等 C．是三角形三条角平分线的交点 D．是三角形三条中线的交点 图K－24－1‎ ‎3．2017·市中区三模如图K－24－1，在平面直角坐标系xOy中，点A的坐标为(0，3)，点B的坐标为(2，1)，点C的坐标为(2，－3)．则经画图操作可知：△ABC的外心坐标应是(　　)‎ A．(0，0) B．(1，0)‎ C．(－2，－1) D．(2，0)‎ ‎4．如图K－24－2，AC，BE是⊙O的直径，弦AD与BE交于点F 9‎ ‎，下列三角形中，外心不是点O的是(　　)‎ 图K－24－2‎ A．△ABE B．△ACF C．△ABD D．△ADE ‎5．如图K－24－3，AB是△ABC的外接圆⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，BC＝5，AE＝6，则DE的长为(　　)‎ ‎　　‎ 图K－24－3‎ A．4 B．‎3 C．4 D. ‎6．若点O是△ABC的外心，且∠BOC＝70°，则∠BAC的度数为(　　)‎ A．35° B．110°‎ C．35°或145° D．35°或140°‎ 二、填空题 ‎7．已知△ABC的三条边长分别为‎6 cm，‎8 cm，‎10 cm，则这个三角形的外接圆的面积为________cm2.(结果用含π的代数式表示)‎ ‎8．2017·十堰模拟如图K－24－4，△ABC是⊙O的内接三角形，连接OB，OC，若∠BAC＋∠BOC＝180°，BC＝‎2 cm，则⊙O的半径为________cm.‎ 图K－24－4‎ ‎9．直角三角形两边的长分别为16和12，则此三角形的外接圆半径是________.‎ ‎10．2018·内江已知△ABC的三边长a，b，c满足a＋b2＋|c－6|＋28＝4 ＋10b，则△ABC的外接圆半径为________．‎ 三、解答题 ‎11．如图K－24－5，已知弧上三点A，B，C.‎ ‎(1)用尺规作图法，找出所在圆的圆心O(保留作图痕迹，不写作法)；‎ ‎(2)设△ABC为等腰三角形，底边BC＝‎16 cm，腰AB＝‎10 cm，求圆片的半径R.‎ 9‎ 图K－24－5‎ 9‎ ‎12.2017·安徽如图K－24－6，在四边形ABCD中，AD＝BC，∠B＝∠D，AD不平行于BC，过点C作CE∥AD交△ABC的外接圆⊙O于点E，连接AE.‎ ‎(1)求证：四边形AECD为平行四边形；‎ ‎(2)连接CO，求证：CO平分∠BCE.‎ 图K－24－6‎ ‎13．如图K－24－7，O为平面直角坐标系的原点，点A的坐标为(6，8)，点B的坐标为(12，0)．‎ ‎(1)求证：AO＝AB；‎ ‎(2)用直尺和圆规作出△AOB的外心P；‎ ‎(3)求点P的坐标．‎ 图K－24－7‎ 9‎ ‎14．如图K－24－8，D是△ABC 的边BC 的中点，过AD延长线上的点E作AD的垂线EF，E为垂足，EF与AB的延长线相交于点F，点O在AD 上，AO＝CO，BC∥EF.‎ ‎(1)求证：AB＝AC；‎ ‎(2)求证：点O是△ABC外接圆的圆心；‎ ‎(3)当AB＝5，BC＝6时，连接BE，若∠ABE＝90°，求AE的长．‎ 图K－24－8‎ 探究题我们知道：过任意一个三角形的三个顶点都能作一个圆，那么我们来探究过四边形四个顶点作圆的条件．‎ ‎(1)分别测量图K－24－9①②③中四边形的内角．如果过某个四边形的四个顶点能作一个圆，那么其相对的两个角之间有什么关系？‎ 图K－24－9‎ ‎(2)如果过某个四边形的四个顶点不能作一个圆，那么其相对的两个角之间有上面的关系吗？试结合图K－24－9④⑤说明其中的道理(提示：考虑∠B＋∠D与180°之间的关系)；‎ ‎(3)由上面的探究，试归纳出判定过四边形的四个顶点能作一个圆的条件．‎ 9‎ 详解详析 ‎【课时作业】‎ ‎[课堂达标]‎ ‎1．[答案] B ‎2．[答案] A ‎3．[解析] C　∵△ABC的外心就是三角形三边垂直平分线的交点，∴作图如图，‎ ‎∴EF与MN的交点O′就是所求的△ABC的外心，∴△ABC的外心坐标是(－2，－1)．故选C.‎ ‎4．[解析] B　只有△ACF的三个顶点不都在圆上，故外心不是点O的是△ACF.‎ ‎5．[解析] C　∵OD⊥AC，∴AE＝CE＝6.∵AB是△ABC的外接圆⊙O的直径，∴∠ACB＝90°，∴AB＝＝＝13.∵OA＝OB，AE＝CE，∴OE为△ABC的中位线，∴OE＝BC＝2.5，∴DE＝OD－OE＝×13－2.5＝4.故选C.‎ ‎6．[解析] C　①当点O在三角形的内部时，‎ 如图①所示，则∠BAC＝∠BOC＝35°；‎ ‎②当点O在三角形的外部时，如图②所示，则∠BAC＝(360°－70°)＝145°.故选C.‎ ‎7．[答案] 25π ‎[解析] 因为62＋82＝102，所以△ABC为直角三角形，且斜边长为‎10 cm，则其外接圆的半径为‎5 cm，所以外接圆的面积为25π cm2.‎ ‎8．[答案] 2‎ ‎[解析] 如图，过点O作OE⊥BC于点E.‎ ‎∵∠BAC＋∠BOC＝180°，∠BOC＝2∠BAC，‎ ‎∴∠BOC＝120°，∠BAC＝60°.‎ 9‎ ‎∵OE⊥BC，‎ ‎∴BE＝EC＝，∠BOE＝∠COE＝60°，∴∠OBE＝30°，∴OB＝2OE.‎ 设OE＝x cm，则OB＝2x cm，∴4x2＝x2＋()2，∴x＝1(负值已舍去)，∴OB＝2 cm.‎ ‎9．[答案] 10或8‎ ‎[解析] 分类讨论：①当16和12是两直角边长时，可得此直角三角形的斜边长为20，其外接圆的半径为10；②当16和12分别是斜边长和直角边长时，可由直角三角形的外接圆半径为直角三角形斜边长的一半，知其外接圆的半径为8.‎ ‎10．[答案] ‎[解析] 原式整理，得b2－10b＋25＋a－1－4 ＋4＋|c－6|＝0，即(b－5)2＋()2－4 ＋4＋|c－6|＝0，(b－5)2＋(－2)2＋|c－6|＝0.∵(b－5)2≥0，(－2)2≥0，|c－6|≥0，∴b＝5，a＝5，c＝6，∴△ABC为等腰三角形．如图所示，过点C作CD⊥AB，设O为外接圆的圆心，则OA＝OC＝R，∵AC＝BC＝5，AB＝6，∴AD＝BD＝3，∴CD＝＝4，∴OD＝CD－OC＝4－R.在Rt△AOD中，R2＝32＋(4－R)2，解得R＝.‎ ‎11．[解析] (1)作AB，AC的中垂线即得圆心O；(2)已知BC和AB的长度，所以可以构造直角三角形，利用勾股定理可求得半径R.‎ 解： (1)如图，作AB，AC的垂直平分线，垂直平分线的交点就是圆心，标出圆心O.‎ ‎(2)连接AO交BC于点E，连接BO.∵AB＝AC，∴＝，‎ ‎∴AE⊥BC，‎ ‎∴BE＝BC＝8 cm.‎ 在Rt△ABE中，AE＝＝＝6(cm)．‎ 在Rt△OBE中，R2＝82＋(R－6)2，‎ 解得R＝ cm，即圆片的半径R为 cm.‎ ‎12．证明：(1)由圆周角定理，得∠B＝∠E.‎ 又∠B＝∠D，∴∠E＝∠D.‎ ‎∵CE∥AD，∴∠D＋∠ECD＝180°，‎ ‎∴∠E＋∠ECD＝180°，‎ ‎∴AE∥CD，∴四边形AECD为平行四边形．‎ 9‎ ‎(2)如图，过点O作OM⊥BC于点M，ON⊥CE于点N，‎ ‎∵四边形AECD为平行四边形，∴AD＝CE.‎ 又AD＝BC，∴CE＝BC，‎ ‎∴OM＝ON.‎ 又OM⊥BC，ON⊥CE，∴CO平分∠BCE.‎ ‎13．解：(1)证明：过点A作AC⊥x轴于点C.‎ ‎∵A(6，8)，∴OC＝6，AC＝8.‎ ‎∵B(12，0)，∴OB＝12，∴BC＝6＝OC，‎ ‎∴AC是OB的垂直平分线，∴AO＝AB.‎ ‎(2)如图，作OA的垂直平分线交AC于点P，点P就是所求的外心．‎ ‎(3)连接PO.‎ ‎∵点P是△AOB的外心，∴PA＝PO＝r.∵AC＝8，∴PC＝8－r.‎ 在Rt△POC中，PO2＝OC2＋PC2，‎ ‎∴r2＝62＋(8－r)2，‎ 解得r＝，∴PC＝，∴P.‎ ‎14．解：(1)证明：∵AE⊥EF，EF∥BC，∴AD⊥BC.‎ 又∵D是BC的中点，‎ ‎∴AD是BC的垂直平分线，∴AB＝AC.‎ ‎(2)证明：连接BO，由(1)知AD是BC的垂直平分线，∴BO＝CO.‎ 又∵AO＝CO，∴AO＝BO＝CO，‎ ‎∴点O是△ABC外接圆的圆心．‎ ‎(3)解法1：∵∠ABE＝∠ADB＝90°，‎ ‎∴∠ABD＋∠BAD＝∠AEB＋∠BAE＝90°，‎ ‎∴∠ABD＝∠AEB.‎ 又∵∠BAD＝∠EAB，‎ ‎∴△ABD∽△AEB，∴＝.‎ 9‎ 在Rt△ABD中，∵AB＝5，BD＝BC＝3，‎ ‎∴AD＝4，∴AE＝. ‎ 解法2：由(2)得AO＝BO，∴∠ABO＝∠BAO.‎ ‎∵∠ABE＝90°，‎ ‎∴∠ABO＋∠OBE＝∠BAO＋∠OEB＝90°，‎ ‎∴∠OBE＝∠OEB，∴OB＝OE.‎ 在Rt△ABD中，∵AB＝5，BD＝BC＝3，‎ ‎∴AD＝4.设 OB＝x, 则 OD＝4－x，‎ 由32＋(4－x)2＝x2，解得x＝，‎ ‎∴AE＝2OB＝.‎ ‎[素养提升]‎ 解：(1)对角互补(对角之和等于180°)．‎ ‎(2)没有．题图④中，∠B＋∠D＜180°；‎ 题图⑤中，∠B＋∠D＞180°.‎ ‎(3)过四边形的四个顶点能作一个圆的条件是：四边形的对角互补(对角之和等于180°)．‎ 9‎