2010年广东省梅州市中考数学试卷 15页

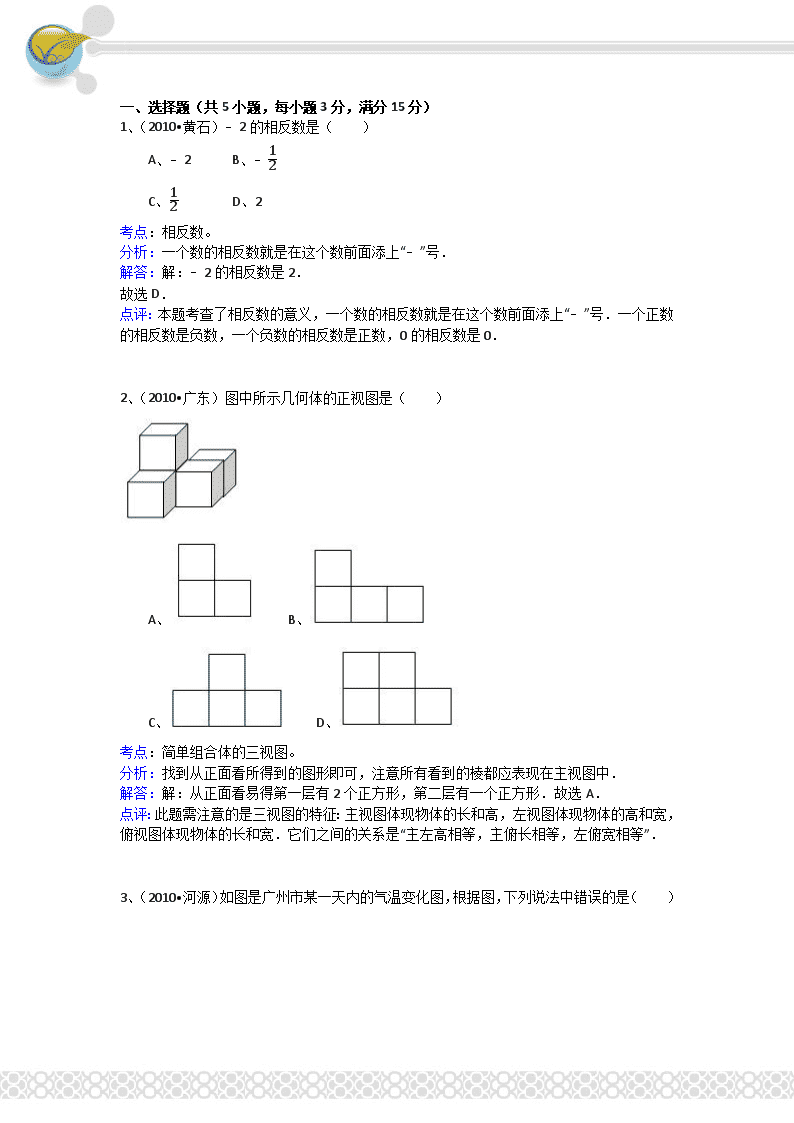
一、选择题（共5小题，每小题3分，满分15分）‎ ‎1、（2010•黄石）﹣2的相反数是（　　）‎ ‎ A、﹣2 B、﹣‎‎1‎‎2‎ ‎ C、‎1‎‎2‎ D、2‎ 考点：相反数。‎ 分析：一个数的相反数就是在这个数前面添上“﹣”号．‎ 解答：解：﹣2的相反数是2．‎ 故选D．‎ 点评：本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“﹣”号．一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．‎ ‎2、（2010•广东）图中所示几何体的正视图是（　　）‎ ‎ A、 B、‎ ‎ C、 D、‎ 考点：简单组合体的三视图。‎ 分析：找到从正面看所得到的图形即可，注意所有看到的棱都应表现在主视图中．‎ 解答：解：从正面看易得第一层有2个正方形，第二层有一个正方形．故选A．‎ 点评：此题需注意的是三视图的特征：主视图体现物体的长和高，左视图体现物体的高和宽，俯视图体现物体的长和宽．它们之间的关系是“主左高相等，主俯长相等，左俯宽相等”．‎ ‎3、（2010•河源）如图是广州市某一天内的气温变化图，根据图，下列说法中错误的是（　　）‎ ‎ A、这一天中最高气温是24℃ B、这一天中最高气温与最低气温的差为16℃‎ ‎ C、这一天中2时至14时之间的气温在逐渐升高 D、这一天中只有14时至24时之间的气温在逐渐降低 考点：函数的图象。‎ 分析：根据广州市某一天内的气温变化图，分析变化趋势和具体数值，即可求出答案．‎ 解答：解：0时至2时之间和14时至24时之间的气温在逐渐降低，剩下时段气温逐渐上升，所以其中A、B、C的说法都是正确的，故选D．‎ 点评：本题考查的是统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．‎ ‎4、（2010•江津区）在函数y=x+1‎中，自变量x的取值范围是（　　）‎ ‎ A、x＞1 B、x≠1‎ ‎ C、x＞﹣1 D、x≥﹣1‎ 考点：函数自变量的取值范围；二次根式有意义的条件。‎ 分析：根据二次根式的性质，被开方数大于等于0可求自变量x的取值范围．‎ 解答：解：根据题意得：x+1≥0，‎ 解得：x≥﹣1．‎ 故选D．‎ 点评：函数自变量的范围一般从三个方面考虑：‎ ‎（1）当函数表达式是整式时，自变量可取全体实数；‎ ‎（2）当函数表达式是分式时，考虑分式的分母不能为0；‎ ‎（3）当函数表达式是二次根式时，被开方数非负．‎ ‎5、（2010•河源）下列图形中，是轴对称图形而不是中心对称图形的是（　　）‎ ‎ A、圆 B、正方形 ‎ C、矩形 D、正三角形 考点：中心对称图形；轴对称图形。‎ 分析：根据轴对称图形与中心对称图形的概念求解．‎ 如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．‎ 如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．‎ 解答：解：A、是轴对称图形，也是中心对称图形，不符合题意；‎ B、是轴对称图形，也是中心对称图形，不符合题意；‎ C、是轴对称图形，也是中心对称图形，不符合题意；‎ D、是轴对称图形，不是中心对称图形，符合题意．‎ 故选D．‎ 点评：掌握中心对称图形与轴对称图形的概念．‎ 判断轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；‎ 判断中心对称图形是要寻找对称中心，图形旋转180度后与原图形重合．‎ 二、填空题（共9小题，满分31分）‎ ‎6、（2010•广东）已知△ABC中，BC=6cm，E、F分别是AB、AC的中点，那么EF长是 cm．‎ 考点：三角形中位线定理。‎ 分析：利用三角形的中位线定理，知EF是BC的一半，可求出EF．‎ 解答：解：∵△ABC中，E、F分别是AB、AC的中点，‎ ‎∴EF是△ABC的中位线，‎ ‎∵BC=6cm，‎ ‎∴EF=‎1‎‎2‎BC=‎1‎‎2‎×6=3cm．‎ 故答案为3．‎ 点评：本题考查了三角形中位线的性质，本题考查了中位线的性质，三角形的中位线是指连接三角形两边中点的线段，中位线的特征是平行于第三边且等于第三边的一半．‎ ‎7、（2010•河源）已知反比例函数y=kx（k≠0）的图象经过点（1，﹣1），则k= ．‎ 考点：反比例函数图象上点的坐标特征。‎ 专题：计算题。‎ 分析：把点（1，﹣1）代入反比例函数解析式即可求得k的值．‎ 解答：解：把点（1，﹣1）代入得：k=1×（﹣1）=﹣1．‎ 故答案为：﹣1．‎ 点评：本题主要考查反比例函数图象上点的坐标特征，反比例函数的比例系数等于在函数图象上面的点的横纵坐标的乘积．‎ ‎8、（2010•宿迁）因式分解：a2﹣1= ．‎ 考点：因式分解-运用公式法。‎ 分析：‎ 考查了对平方差公式的理解，本题属于基础题．本题中两个平方项的符号相反，直接运用平方差公式分解因式．‎ 解答：解：a2﹣1=a2﹣12=（a+1）（a﹣1）．‎ 点评：本题考查了公式法分解因式，熟记能用平方差公式分解因式的多项式的特征，即“两项、异号、平方形式”是避免错用平方差公式的有效方法．‎ ‎9、（2010•河源）甲，乙，丙，丁四支足球队在世界杯预选赛中的进球数分别为：9，9，11，7，则这组数据的：①众数为 ；②中位数为 ；③平均数为 ．‎ 考点：众数；算术平均数；中位数。‎ 分析：根据平均数，中位数，众数的概念求解即可．‎ 解答：解：①数据9出现2次，次数最多，所以众数是9；‎ ‎②数据按从小到大排列：7，9，9，11，所以中位数是（9+9）÷2=9；‎ ‎③平均数=（9+9+11+7）÷4=9．‎ 故填9；9；9．‎ 点评：本题考查了平均数，中位数，众数的意义．平均数是指在一组数据中所有数据之和再除以数据的个数．众数是一组数据中出现次数最多的数据，注意众数可以不止一个．找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数．如果数据有奇数个，则正中间的数字即为所求；如果是偶数个，则找中间两个数的平均数．‎ ‎10、（2010•广东）为支援玉树灾区，我市党员捐款近600万元，600万用科学记数法表示为 ．‎ 考点：科学记数法—表示较大的数。‎ 专题：应用题。‎ 分析：应先把600万元整理为用元表示的数，进而整理为a×10n的形式．‎ 解答：解：600万元=6 000 000元=6×106元．‎ 点评：将一个绝对值较大的数写成科学记数法a×10n的形式时，其中1≤|a|＜10，n为比整数位数少1的数．注意万字相当于把原数扩大10 000倍．‎ ‎11、（2010•河源）若x1，x2是一元二次方程x2﹣2x﹣1=0的两个根，则x1+x2的值等于 ．‎ 考点：根与系数的关系。‎ 分析：一元二次方程中，根与系数的关系是x1+x2=﹣ba，x1•x2=ca．‎ 解答：解：根据一元二次方程的根与系数的关系，得 x1+x2=﹣‎﹣2‎‎1‎，即x1+x2=2．‎ 点评：本题主要考查了一元二次方程的根与系数的关系．‎ ‎12、（2010•广东）已知一个圆锥的母线长为2cm ‎，它的侧面展开图恰好是一个半圆，则这个圆锥的侧面积等于 cm2（用含π的式子表示）．‎ 考点：圆锥的计算。‎ 分析：圆锥的侧面积等于母线长乘底面周长的一半．依此公式计算即可．‎ 解答：解：底面周长=2×2×π÷2=2πcm 侧面积=2π×2÷2=2πcm2．‎ 点评：本题主要考查了圆锥的侧面积的计算公式．‎ ‎13、（2010•河源）平面内不过同一点的n条直线两两相交，它们的交点个数记作an，并且规定a1=0．那么：①a2= ；②a3﹣a2= ；③an﹣an﹣1= ．（n≥2，用含n的代数式表示）．‎ 考点：直线、射线、线段。‎ 专题：规律型。‎ 分析：n条直线相交，最多有1+2+3+…+（n﹣1）=‎1‎‎2‎n（n﹣1）‎个交点．‎ 解答：解：①a2=‎1‎‎2‎n（n﹣1）‎=1；‎ ‎②∵a3=3，a2=1‎ ‎∴a3﹣a2=3﹣1=2；‎ ‎③an﹣an﹣1=‎1‎‎2‎n（n﹣1）‎﹣‎1‎‎2‎（n﹣1）（n﹣2）=‎1‎‎2‎（n﹣1）（n﹣n+2）=n﹣1．‎ 点评：此题在相交线的基础上，着重培养学生的观察、实验和猜想、归纳能力，掌握从特殊项一般猜想的方法．‎ ‎14、（2010•河源）Rt△ABC中，∠C=90°，∠A=60°，AC=2．按以下步骤作图：‎ ‎①以A为圆心，以小于AC长为半径画弧，分别交AC、AB于点E、D ‎②分别以D、E为圆心，以大于‎1‎‎2‎DE长为半径画弧，两弧相交于点P ‎③连接AP交BC于点F．‎ 那么：（1）AB的长等于 ；（直接填写答案）‎ ‎（2）∠CAF= 度．（直接填写答案）．‎ 考点：含30度角的直角三角形；全等三角形的判定与性质。‎ 专题：作图题。‎ 分析：（1）根据30°所对的直角边是斜边的一半进行求解；‎ ‎（2）根据作图的步骤易证明AF是∠BAC的平分线，即可求解．‎ 解答：解：（1）∵，∠C=90°，∠A=60°，AC=2，‎ ‎∴AB=2AC=4．‎ ‎（2）根据作图，得 AD=AE，PD=PE，AP=AP，‎ 则△AEP≌△ADP．‎ ‎∴∠CAF=30°．‎ 点评：本题考查了全等三角形的性质与判定；综合运用了30°的直角三角形的性质以及全等三角形的判定和性质．‎ 三、解答题（共9小题，满分74分）‎ ‎15、（2010•河源）计算：|﹣2|﹣（‎1‎‎2‎）﹣1+（π﹣3.14）0+‎8‎×cos45°‎ 考点：特殊角的三角函数值；零指数幂；负整数指数幂。‎ 专题：计算题。‎ 分析：本题涉及零指数幂、负指数幂、二次根式化简、绝对值、特殊角的三角函数值5个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．‎ 解答：解：原式=2﹣2+1+2‎2‎×‎‎2‎‎2‎ ‎=1+2=3 ．‎ 点评：本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值，特殊角的三角函数值等考点的运算．‎ ‎16、（2010•河源）解方程：‎1‎x‎2‎‎﹣x=‎‎2‎x‎2‎‎﹣2x+1‎ 考点：解分式方程。‎ 专题：计算题。‎ 分析：把各分母因式分解后可得本题的最简公分母是x（x﹣1）2，方程两边都乘最简公分母，可把分式方程转换为整式方程求解．‎ 解答：解：方程两边都乘x（x﹣1）2，得：x﹣1=2x 移项及合并得x=﹣1，‎ 经检验x=﹣1是原分式方程的解，‎ ‎∴x=﹣1．‎ 点评：（1）解分式方程的基本思想是“转化思想”，方程两边都乘最简公分母，把分式方程转化为整式方程求解．‎ ‎（2）解分式方程一定注意要代入最简公分母验根．‎ ‎17、（2010•河源）在平面直角坐标系中，点M的坐标为（a，﹣2a）．‎ ‎（1）当a=﹣1时，点M在坐标系的第 象限；（直接填写答案）‎ ‎（2）将点M向左平移2个单位，再向上平移1个单位后得到点N，当点N在第三象限时，求a的取值范围．‎ 考点：坐标与图形变化-平移。‎ 分析：（1）当a=﹣1时点M的坐标为（﹣1，2），所以M在第二象限；‎ ‎（2）根据平移方法，可得到N点坐标，N在第三象限，所以横坐标小于0，纵坐标小于0解不等式组可得a的取值范围．‎ 解答：解：（1）当a=﹣1时点M的坐标为（﹣1，2），所以M在第二象限，所应填“二”；‎ ‎（2）将点M向左平移2个单位，再向上平移1个单位后得到点N，点M的坐标为（a，﹣2a），所以N点坐标为（a﹣2，﹣2a+1），因为N点在第三象限，所以‎&a﹣2＜0‎‎&﹣2a+1＜0‎，解得‎1‎‎2‎＜a＜2，所以a的取值范围为‎1‎‎2‎＜a＜2．‎ 点评：本题考查图形的平移变换．关键是要懂得左右平移点的纵坐标不变，而上下平移时点的横坐标不变．‎ ‎18、（2010•河源）（1）如图1，PA，PB分别与圆O相切于点A，B．求证：PA=PB；‎ ‎（2）如图2，过圆O外一点P的两条直线分别与圆O相交于点A、B和C、D．则当 时，PB=PD．（不添加字母符号和辅助线，不需证明，只需填上符合题意的一个条件）‎ 考点：切线的性质；全等三角形的判定与性质。‎ 专题：证明题；开放型。‎ 分析：（1）连接OA、OB．则OA⊥PA，OB⊥PB．根据HL证明△POA≌△POB，得证；‎ ‎（2）若PB=PD，则易证△POB≌△POD，有∠BPO=∠DPO．所以可填∠BPO=∠DPO．‎ 解答：（1）证明：连接OA、OB．‎ ‎∵PA、PB是切线，‎ ‎∴OA⊥PA，OB⊥PB．‎ ‎∵OA=OB，OP公共，‎ ‎∴△POA≌△POB，‎ ‎∴PA=PB．‎ ‎（2）当∠BPO=∠DPO时，PB=PD．‎ 证明：作⊥AB于M，ON⊥CD于N．‎ ‎∵∠BPO=∠DPO，‎ ‎∴OM=ON．‎ ‎∴AB=CD．则BM=DN．‎ ‎∵OM=ON，OP公共，‎ ‎∴△POM≌△PON，‎ ‎∴PM=PN．‎ ‎∴PB=PD．‎ 点评：此题考查了切线的性质，拓展题难度也不大．‎ ‎19、（2010•河源）如图，东梅中学要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园，矩形的一边用教学楼的外墙，其余三边用竹篱笆．设矩形的宽为x，面积为y．‎ ‎（1）求y与x的函数关系式，并求自变量x的取值范围；‎ ‎（2）生物园的面积能否达到210平方米？说明理由．‎ 考点：二次函数的应用。‎ 分析：（1）设矩形的宽为x，则长为40﹣2x，根据矩形面积公式“面积=长×宽”列出函数的关系式．‎ ‎（2）令y=210，看函数方程有没有解？‎ 解答：解：（1）设矩形的宽为x，则长为40﹣2x，‎ y=x（40﹣2x）=﹣2x2+40x又要围成矩形，则40﹣2x＞0，x＜20‎ x的取值范围：0＜x＜20‎ ‎（2）令y=210，则﹣2x2+40x=210变形得：‎ ‎2x2﹣40x+210=0‎ 又∵△=40×40﹣4×2×210＜0‎ ‎∴方程无解，‎ ‎∴生物园的面积达不到210平方米．‎ 点评：本题考查的是函数关系式的求法及最值的求法，同学们应该掌握．‎ ‎20、（2010•河源）某校九年级有200名学生参加了全国初中数学联合竞赛的初赛，为了了解本次初赛的成绩情况，从中抽取了50名学生，将他们的初赛成绩（得分为整数，满分为100分）分成五组：第一组49.5～59.5；第二组59.5～69.5；第三组69.5～79.5；第四组79.5～89.5；第五组89.5～100.5．统计后得到图所示的频数分布直方图（部分）．‎ 观察图形的信息，回答下列问题：‎ ‎（1）第四组的频数为 ；（直接填写答案）‎ ‎（2）若将得分转化为等级，规定：得分低于59.5分评为“D”，59.5～69.5分评为“C”，69.5～89.5分评为“B”，89.5～100.5分评为“A”．那么这200名参加初赛的学生中，参赛成绩评为“D”的学生约有 个．（直接填写答案）‎ ‎（3）若将抽取出来的50名学生中成绩落在第四、第五组的学生组成一个培训小组，再从这个培训小组中随机挑选2名学生参加决赛．用列表法或画树状图法求：挑选的2名学生的初赛成绩恰好都在90分以上的概率．‎ 考点：频数（率）分布直方图；用样本估计总体；列表法与树状图法。‎ 专题：图表型。‎ 分析：（1）用样本容量50分别减去其它各组的人数，既得第四组的频数；‎ ‎（2）根据频数分布直方图可知，50个人中参赛成绩评为“D”的学生有16，求出所占的百分比，再乘以200即可；‎ ‎（3）由题意可知第四组的频数是2，第五组的频数也是2，设第四组的2名学生分别为A1、A2第五组的2名学生为B1、B2，列表（或画树状图），通过图表确定恰好都是在90分以上的概率．‎ 解答：解：（1）第四组的频数为：50﹣16﹣20﹣10﹣2=2；‎ ‎（2）参赛成绩评为“D”的学生约有：200×‎16‎‎50‎=64（人）；‎ ‎（3）依题得第四组的频数是2，第五组的频数也是2，设第四组的2名学生分别为A1、A2第五组的2名学生为B1、B2，列表（或画树状图）如下：（5‎ 由上表可知共有12种结果，其中两个都是90分以上的有两种结果，所以恰好都是在90分以上的概率为‎1‎‎6‎．‎ 点评：本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．用到的知识点为：各小组频数之和等于样本总数；概率=所求情况数与总情况数之比．‎ ‎21、（2010•河源）东艺中学初三（1）班学生到雁鸣湖春游，有一项活动是划船．游船有两种，甲种船每条船最多只能坐4个人，乙种船每条船最多只能坐6个人．已知初三（1）班学生的人数是5的倍数，若仅租甲种船，则不少于12条；若仅租乙种船，则不多于9条．‎ ‎（1）求初三（1）班学生的人数；‎ ‎（2）如果甲种船的租金是每条船10元，乙种船的租金是每条船12元．应怎样租船，才能使每条船都坐满，且租金最少？说明理由．‎ 考点：一元一次不等式组的应用。‎ 专题：应用题。‎ 分析：（1）设初三（1）班学生的人数为5x人，根据实际人数不小于12×4人，不大于9×6人，列不等式组即可求解；‎ ‎（2）租乙种船能使每条船坐满而且租金最少．因为甲种船每条10元，一条船最多坐四个人，初三（1）50个人须要13条船租金就是130元．而乙种船租金12元，一条船最多坐六个人，50个人须要9条船租金就是108元，而使用8条乙船，1条甲船的租金为106元．‎ 解答：解：设初三（1）班学生的人数为5x人，则 ‎&5x≥12×4‎‎&5x≤9×6‎ 解得9‎3‎‎5‎≤x≤10‎‎4‎‎5‎ 因为x是整数，所以x=10‎ 即5x=50 ．‎ 答：初三（1）班学生的人数为50人．‎ ‎（2）设租金为w元，租甲船x条，乙船y条，则 ‎4x+6y=50‎ w=10x+12y 所以w=﹣3y+125‎ w随着y的增大而减小，故当y取最大值时，w最小 因为50÷6=8‎1‎‎3‎，所以取y=8，x=1时租金最少为 w=﹣3×7+125=104（元） ．‎ 即使用8条乙船，1条甲船的租金最少为104元．‎ 点评：本题考查一元一次不等式组的应用，将现实生活中的事件与数学思想联系起来，读懂题列出不等式关系式即可求解．要注意根据实际问题来求租金的最小值．‎ ‎22、（2010•河源）如图，△ABC中，点P是边AC上的一个动点，过P作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．‎ ‎（1）求证：PE=PF；‎ ‎（2）当点P在边AC上运动时，四边形AECF可能是矩形吗？说明理由；‎ ‎（3）若在AC边上存在点P，使四边形AECF是正方形，且APBC‎=‎‎3‎‎2‎．求此时∠A的大小．‎ 考点：菱形的判定；平行线的性质；正方形的判定。‎ 专题：动点型。‎ 分析：（1）可证明PE=PC，PF=PC，从而得到PE=PF；‎ ‎（2）由一对邻补角的平分线互相垂直，得出∠ECF=90°，故要使四边形AECF是矩形，只需四边形AECF是平行四边形即可．由（1）知PE=PF，则点P运动到AC边中点时，四边形AECF是矩形．‎ ‎（3）由正方形的对角线相等且互相垂直，可知AC⊥EF，AC=2AP．又EF∥BC，得出AC⊥BC，在直角△ABC 中，根据锐角三角函数的定义及特殊角的三角函数值求出∠A的大小．‎ 解答：解：（1）∵CE平分∠BCA，‎ ‎∴∠BCE=∠ECP，‎ 又∵MN∥BC，‎ ‎∴∠BCE=∠CEP，‎ ‎∴∠ECP=∠CEP，‎ ‎∴PE=PC；‎ 同理PF=PC，‎ ‎∴PE=PF；‎ ‎（2）当点P运动到AC边中点时，四边形AECF是矩形．理由如下：‎ 由（1）可知PE=PF，‎ ‎∵P是AC中点，‎ ‎∴AP=PC，‎ ‎∴四边形AECF是平行四边形．‎ ‎∵CE、CF分别平分∠BCA、∠ACD，‎ 且∠BCA+∠ACD=180°，‎ ‎∴∠ECF=∠ECP+∠PCF=‎1‎‎2‎（∠BCA+∠ACD）=‎1‎‎2‎×180°=90°，‎ ‎∴平行四边形AECF是矩形；‎ ‎（3）证明：若四边形AECF是正方形，则AC⊥EF，AC=2AP．‎ ‎∵EF∥BC，‎ ‎∴AC⊥BC，‎ ‎∴△ABC是直角三角形，且∠ACB=90°，‎ ‎∴cot∠A=ACBC‎=‎2APBC=2×‎‎3‎‎2‎=‎3‎，‎ ‎∴∠A=30°．‎ 点评：此题综合考查了平行线的性质，等腰三角形的判定，矩形的判定，正方形的性质，锐角三角函数的定义及特殊角的三角函数值等知识点，难度较大．‎ ‎23、（2010•河源）如图，直角梯形OABC中，OC∥AB，C（0，3），B（4，1），以BC为直径的圆交x轴于E，D两点（D点在E点右方）．‎ ‎（1）求点E，D的坐标；‎ ‎（2）求过B，C，D三点的抛物线的函数关系式；‎ ‎（3）过B，C，D三点的抛物线上是否存在点Q，使△BDQ是以BD为直角边的直角三角形？若不存在，说明理由；若存在，求出点Q的坐标．‎ 考点：二次函数综合题；待定系数法求二次函数解析式；勾股定理的逆定理；直角梯形；圆周角定理。‎ 专题：压轴题。‎ 分析：（1）设以BC为直径的圆的圆心为M，由于⊙M过点D，由圆周角定理可得∠BDC=90°；即可证得△ABD∽△ODC，可用OD表示出DA，根据相似三角形得到的比例线段，即可求得OD的长，由此可得到点D、E的坐标；‎ ‎（2）用待定系数法求解即可求出该抛物线的解析式；‎ ‎（3）首先求出直线CD的解析式；由于CD⊥BD，且点C在抛物线的图象上，因此C点就是符合条件的Q点；同理可先求出过B点且平行于CD的直线l的解析式，直线l与抛物线的交点（B点除外）也应该符合Q点的要求．‎ 解答：解：（1）取BC的中点M，过M作MN⊥x轴于N；则M点即为以BC为直径的圆的圆心；‎ ‎∵点D是⊙M上的点，且BC是直径，‎ ‎∴∠BDC=90°；‎ ‎∴∠OCD=∠BDA=90°﹣∠ODC；‎ 又∵∠COD=∠OAB，‎ ‎∴△OCD∽△ADB；‎ ‎∴ABOD‎=‎ADOC；‎ ‎∵OC=3，AB=1，OA=OD+DA=4，‎ ‎∴3×1=OD×（4﹣OD），‎ 解得OD=1，OD=3；‎ ‎∵点D在点E右边，‎ ‎∴OD=3，OE=1；‎ 即D（3，0），E（1，0）；‎ ‎（2）设抛物线的解析式为y=ax2+bx+c，（a≠0），依题意，‎ 有：‎&c=3‎‎&16a+4b+c=1‎‎&9a+3b+c=0‎，‎ 解得‎&a=‎‎1‎‎2‎‎&b=﹣‎‎5‎‎2‎‎&c=3‎；‎ ‎∴y=‎1‎‎2‎x2﹣‎5‎‎2‎x+3；‎ ‎（3）假设存在这样的Q点；‎ ‎①△BDQ以D为直角顶点；‎ 由于CD⊥BD，且C点在抛物线的图象上，‎ 所以C点符合Q点的要求；‎ 此时Q（0，3）；‎ ‎②△BDQ以B为直角顶点；‎ 易知直线AC的解析式为：y=﹣x+3；‎ 作过B的直线l，且l∥CD；‎ 设l的解析式为y=﹣x+h，由于l经过点B（4，1），‎ 则有：﹣4+h=1，h=5；‎ ‎∴直线l的解析式为y=﹣x+5；‎ 联立抛物线的解析式有：‎ ‎&y=‎1‎‎2‎x‎2‎﹣‎5‎‎2‎x+3‎‎&y=﹣x+5‎‎，‎ 解得‎&x=4‎‎&y=1‎，‎&x=﹣1‎‎&y=6‎；‎ ‎∴Q（﹣1，6）；‎ 综上所述，存在符合条件的Q点，且Q点坐标为（0，3）或（﹣1，6）．‎ 点评：此题主要考查的圆周角定理、相似三角形的判定和性质、二次函数解析式的确定、函数图象交点坐标的求法、直角三角形的判定等知识的综合应用，综合性强，难度较大．‎ 参与本试卷答题和审题的老师有：‎ wangcen；CJX；Linaliu；huangling；py168；张伟东；lanchong；zxw；nhx600；算术；zhjh；lanyuemeng；kuaile；zhangchao；wdxwwzy；HJJ；MMCH；hnaylzhyk；wdxwzk；郭静慧。（排名不分先后）‎ ‎2011年2月17日