2010中考数学河北考试试题 12页

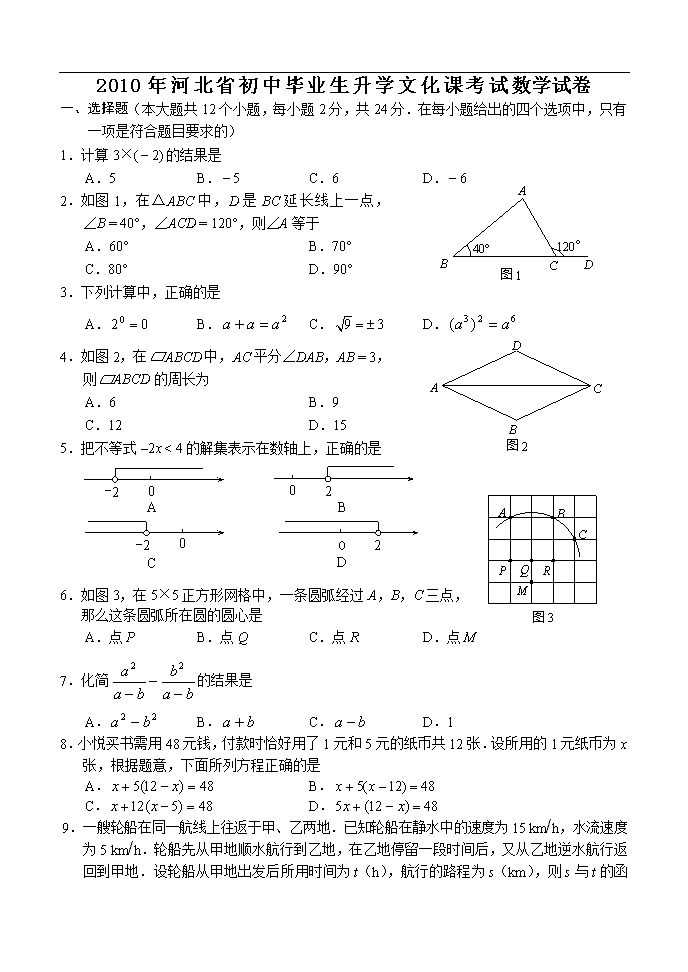
‎2010年河北省初中毕业生升学文化课考试数学试卷 一、选择题（本大题共12个小题，每小题2分，共24分．在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．计算3×(2) 的结果是 A B C D ‎40°‎ ‎120°‎ 图1‎ A．5 B．5 C．6 D．6‎ ‎2．如图1，在△ABC中，D是BC延长线上一点， ‎ ‎∠B = 40°，∠ACD = 120°，则∠A等于 A．60° B．70° ‎ C．80° D．90°‎ ‎3．下列计算中，正确的是 A B C D 图2‎ A． B． C． D．‎ ‎4．如图2，在□ABCD中，AC平分∠DAB，AB = 3， ‎ 则□ABCD的周长为 A．6 B．9 ‎ C．12 D．15‎ ‎5．把不等式< 4的解集表示在数轴上，正确的是 A ‎-2‎ ‎0‎ B D ‎2‎ ‎0‎ C ‎0‎ ‎-2‎ ‎2‎ ‎0‎ ‎ ‎ M R Q 图3‎ A B C P ‎　　　　　　　　　　　　　　　‎ ‎6．如图3，在5×5正方形网格中，一条圆弧经过A，B，C三点， ‎ 那么这条圆弧所在圆的圆心是 A．点P B．点Q C．点R D．点M ‎7．化简的结果是 A． B． C． D．1‎ ‎8．小悦买书需用48元钱，付款时恰好用了1元和5元的纸币共12张．设所用的1元纸币为x张，根据题意，下面所列方程正确的是 A． B． ‎ C． D．‎ ‎9．一艘轮船在同一航线上往返于甲、乙两地．已知轮船在静水中的速度为15 km/h，水流速度为5 km/h．轮船先从甲地顺水航行到乙地，在乙地停留一段时间后，又从乙地逆水航行返回到甲地．设轮船从甲地出发后所用时间为t（h），航行的路程为s（km），则s与t 的函数图象大致是 t s O A t s O B t s O C t s O D 图4‎ ‎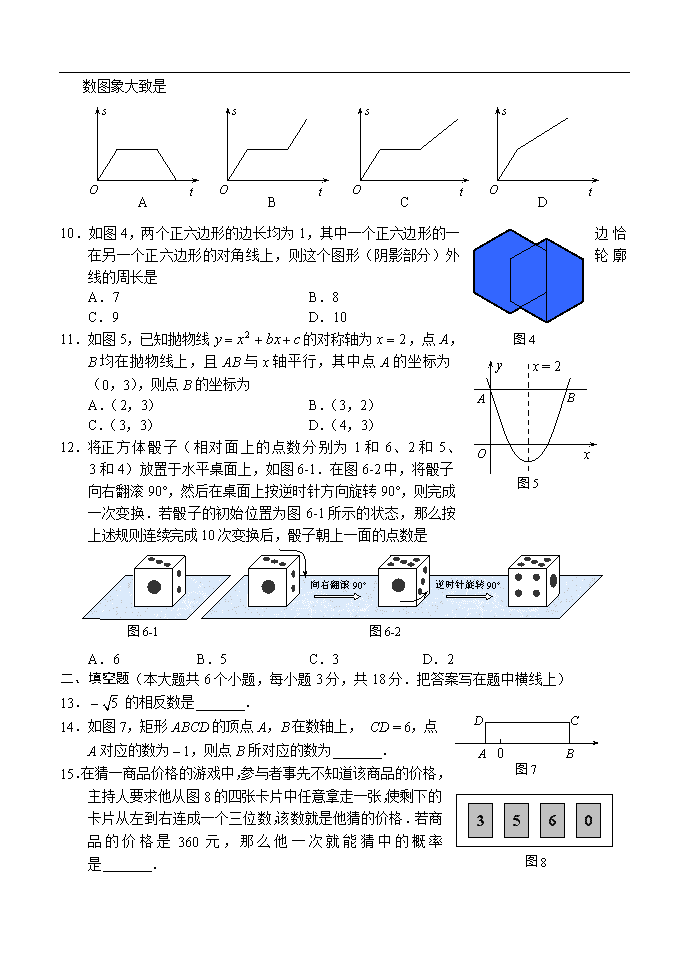10．如图4，两个正六边形的边长均为1，其中一个正六边形的一边恰在另一个正六边形的对角线上，则这个图形（阴影部分）外轮廓线的周长是 A．7 B．8 ‎ C．9 D．10‎ O x y A 图5‎ x = 2‎ B ‎11．如图5，已知抛物线的对称轴为，点A，‎ B均在抛物线上，且AB与x轴平行，其中点A的坐标为 ‎（0，3），则点B的坐标为 A．（2，3） B．（3，2） ‎ C．（3，3） D．（4，3）‎ ‎12．将正方体骰子（相对面上的点数分别为1和6、2和5、‎ ‎3和4）放置于水平桌面上，如图6-1．在图6-2中，将骰子 向右翻滚90°，然后在桌面上按逆时针方向旋转90°，则完成 一次变换．若骰子的初始位置为图6-1所示的状态，那么按 上述规则连续完成10次变换后，骰子朝上一面的点数是 图6-1‎ 图6-2‎ 向右翻滚90°‎ 逆时针旋转90°‎ A．6 B．5 C．3 D．2‎ 二、填空题（本大题共6个小题，每小题3分，共18分．把答案写在题中横线上）‎ ‎13．的相反数是 ．‎ ‎14．如图7，矩形ABCD的顶点A，B在数轴上， CD = 6，点A对应的数为，则点B所对应的数为 ．‎ A ‎0‎ 图7‎ B C D ‎3‎ ‎5‎ ‎6‎ ‎0‎ 图8‎ ‎15．在猜一商品价格的游戏中，参与者事先不知道该商品的价格，主持人要求他从图8的四张卡片中任意拿走一张，使剩下的卡片从左到右连成一个三位数，该数就是他猜的价格．若商品的价格是360元，那么他一次就能猜中的概率是 ．‎ 图9‎ A B O ‎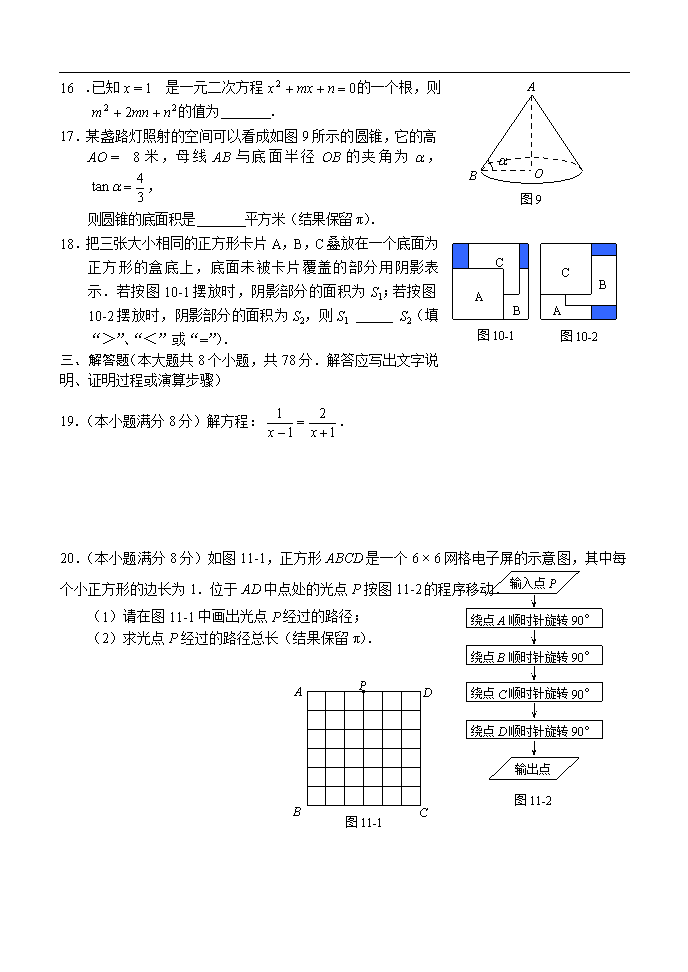16．已知x = 1是一元二次方程的一个根，则 的值为 ． ‎ ‎17．某盏路灯照射的空间可以看成如图9所示的圆锥，它的高AO = 8米，母线AB与底面半径OB的夹角为，，‎ 则圆锥的底面积是 平方米（结果保留π）．‎ 图10-1‎ A C B C B A 图10-2‎ ‎18．把三张大小相同的正方形卡片A，B，C叠放在一个底面为正方形的盒底上，底面未被卡片覆盖的部分用阴影表示．若按图10-1摆放时，阴影部分的面积为S1；若按图10-2摆放时，阴影部分的面积为S2，则S1 S2（填“＞”、“＜”或“=”）．‎ 三、解答题（本大题共8个小题，共78分．解答应写出文字说明、证明过程或演算步骤）‎ ‎19．（本小题满分8分）解方程：．‎ ‎20．（本小题满分8分）绕点A顺时针旋转90°‎ 绕点B顺时针旋转90°‎ 绕点C顺时针旋转90°‎ 图11-2‎ 输入点P 输出点 绕点D顺时针旋转90°‎ 如图11-1，正方形ABCD是一个6 × 6网格电子屏的示意图，其中每个小正方形的边长为1．位于AD中点处的光点P按图11-2的程序移动．‎ ‎（1）请在图11-1中画出光点P经过的路径；‎ ‎（2）求光点P经过的路径总长（结果保留π）．‎ A D 图11-1‎ B C P ‎21．（本小题满分9分）乙校成绩扇形统计图 图12-1‎ ‎10分 ‎9分 ‎8分 ‎72°‎ ‎54°°‎ ‎7分 甲校成绩统计表 甲、乙两校参加区教育局举办的学生英语口语竞赛，两校参赛人数相等．比赛结束后，发现学生成绩分别为7分、8分、9分、10分（满分为10分）．依据统计数据绘制了如下尚不完整的统计图表．‎ 分 数 ‎7 分 ‎8 分 ‎9 分 ‎10 分 人 数 ‎11‎ ‎0‎ ‎8‎ ‎ ‎ ‎（1）在图12-1中，“7分”所在扇形的圆心角 等于 °．‎ ‎（2）请你将图12-2的统计图补充完整．‎ 乙校成绩条形统计图 ‎2‎ ‎8‎ ‎6‎ ‎4‎ ‎8分 ‎9分 分数 人数 ‎2‎ ‎10分 图12-2‎ ‎7分 ‎0‎ ‎8‎ ‎4‎ ‎5‎ ‎（3）经计算，乙校的平均分是8.3分，中位数是8分，请写出甲校的平均分、中位数；并从平均分和中位数的角度分析哪个学校成绩较好．‎ ‎（4）如果该教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析，应选哪所学校？‎ ‎22．（本小题满分9分）‎ 如图13，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标为（4，2）．过点D（0，3）和E（6，0）的直线分别与AB，BC交于点M，N．‎ ‎（1）求直线DE的解析式和点M的坐标；‎ ‎（2）若反比例函数（x＞0）的图象经过点M，求该反比例函数的解析式，并通过计算判断点N是否在该函数的图象上；‎ x M N y D A B C E O 图13‎ ‎（3）若反比例函数（x＞0）的图象与△MNB有公共点，请直接写出m的取值范围．‎ ‎23．（本小题满分10分）‎ 图14-1‎ 连杆 滑块 滑道 观察思考 某种在同一平面进行传动的机械装置如图14-1，图14-2‎ 是它的示意图．其工作原理是：滑块Q在平直滑道l上可以 左右滑动，在Q滑动的过程中，连杆PQ也随之运动，并且 PQ带动连杆OP绕固定点O摆动．在摆动过程中，两连杆的接点P在以OP为半径的⊙O上运动．数学兴趣小组为进一步研 究其中所蕴含的数学知识，过点O作OH ⊥l于点H，并测得 OH = 4分米，PQ = 3分米，OP = 2分米．‎ 解决问题 H l O P Q 图14-2‎ ‎（1）点Q与点O间的最小距离是 分米；‎ 点Q与点O间的最大距离是 分米；‎ 点Q在l上滑到最左端的位置与滑到最右端位置间 的距离是 分米．‎ ‎（2）如图14-3，小明同学说：“当点Q滑动到点H的位 置时，PQ与⊙O是相切的．”你认为他的判断对吗？‎ 为什么？‎ ‎（3）①小丽同学发现：“当点P运动到OH上时，点P到l 的距离最小．”事实上，还存在着点P到l距离最大 的位置，此时，点P到l的距离是 分米；‎ H l O 图14-3‎ P ‎（Q）‎ ‎②当OP绕点O左右摆动时，所扫过的区域为扇形，‎ 求这个扇形面积最大时圆心角的度数．‎ ‎ ‎ 图15-2‎ A D O B C ‎2‎ ‎1‎ M N 图15-1‎ A D B M N ‎1‎ ‎2‎ 图15-3‎ A D O B C ‎2‎ ‎1‎ M N O ‎24．（本小题满分10分）‎ 在图15-1至图15-3中，直线MN与线段AB相交 于点O，∠1 = ∠2 = 45°．‎ ‎（1）如图15-1，若AO = OB，请写出AO与BD ‎ 的数量关系和位置关系；‎ ‎（2）将图15-1中的MN绕点O顺时针旋转得到 图15-2，其中AO = OB．‎ 求证：AC = BD，AC ⊥ BD；‎ ‎（3）将图15-2中的OB拉长为AO的k倍得到 图15-3，求的值．‎ ‎25．（本小题满分12分）‎ 如图16，在直角梯形ABCD中，AD∥BC，，AD = 6，BC = 8，，点M是BC的中点．点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动．在点P，Q的运动过程中，以PQ为边作等边三角形EPQ，使它与梯形ABCD在射线BC的同侧．点P，Q同时出发，当点P返回到点M时停止运动，点Q也随之停止．‎ 设点P，Q运动的时间是t秒(t＞0)．‎ ‎（1）设PQ的长为y，在点P从点M向点B运动的过程中，写出y与t之间的函数关系式（不必写t的取值范围）．‎ ‎（2）当BP = 1时，求△EPQ与梯形ABCD重叠部分的面积．‎ M A D C B P Q E 图16‎ A D C B ‎（备用图）‎ M ‎（3）随着时间t的变化，线段AD会有一部分被△EPQ覆盖，被覆盖线段的长度在某个时刻会达到最大值，请回答：该最大值能否持续一个时段？若能，直接写出t的取值范围；若不能，请说明理由．‎ ‎26．（本小题满分12分）‎ 某公司销售一种新型节能产品，现准备从国内和国外两种销售方案中选择一种进行销售．‎ 若只在国内销售，销售价格y（元/件）与月销量x（件）的函数关系式为y =x＋150，‎ 成本为20元/件，无论销售多少，每月还需支出广告费62500元，设月利润为w内（元）（利润 = 销售额－成本－广告费）．‎ 若只在国外销售，销售价格为150元/件，受各种不确定因素影响，成本为a元/件（a为 常数，10≤a≤40），当月销量为x（件）时，每月还需缴纳x2 元的附加费，设月利润为w外（元）（利润 = 销售额－成本－附加费）．‎ ‎（1）当x = 1000时，y = 元/件，w内 = 元；‎ ‎（2）分别求出w内，w外与x间的函数关系式（不必写x的取值范围）；‎ ‎（3）当x为何值时，在国内销售的月利润最大？若在国外销售月利润的最大值与在国内销售月利润的最大值相同，求a的值；‎ ‎（4）如果某月要将5000件产品全部销售完，请你通过分析帮公司决策，选择在国内还是在国外销售才能使所获月利润较大？‎ 参考公式：抛物线的顶点坐标是．‎ ‎2010年河北省初中毕业生升学文化课考试 数学试题参考答案 一、选择题 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 案 D C D C A B B A C B D B 二、填空题 ‎13. 14.5 15. 16.1 17.36 π 18. = ‎ 三、解答题 ‎19．解：， ． ‎ A D 图1‎ B C P 经检验知，是原方程的解． ‎ ‎20．解： （1）如图1；‎ ‎【注：若学生作图没用圆规，所画路线光滑且基本准确即给4分】‎ ‎（2）∵，‎ ‎∴点P经过的路径总长为6 π． ‎ ‎21．解：（1）144；‎ 乙校成绩条形统计图 ‎2‎ ‎8‎ ‎6‎ ‎4‎ ‎8分 ‎9分 分数 人数 ‎2‎ ‎10分 图2‎ ‎7分 ‎0‎ ‎8‎ ‎3‎ ‎4‎ ‎5‎ ‎（2）如图2； ‎ ‎（3）甲校的平均分为8.3分，中位数为7分；‎ 由于两校平均分相等，乙校成绩的中位数大于甲 校的中位数，所以从平均分和中位数角度上判断，‎ 乙校的成绩较好． ‎ ‎（4）因为选8名学生参加市级口语团体赛，甲校得 ‎10分的有8人，而乙校得10分的只有5人，所以应选甲校． ‎ ‎22．解：（1）设直线DE的解析式为，‎ ‎∵点D ，E的坐标为（0，3）、（6，0），∴ ‎ 解得 ∴ ． ‎ ‎∵ 点M在AB边上，B（4，2），而四边形OABC是矩形，‎ ‎∴ 点M的纵坐标为2．‎ 又 ∵ 点M在直线上，‎ ‎∴ 2 = ．∴ x = 2．∴ M（2，2）． ‎ ‎（2）∵（x＞0）经过点M（2，2），∴ ．∴. ‎ 又 ∵ 点N在BC边上，B（4，2），∴点N的横坐标为4．‎ ‎∵ 点N在直线上， ∴ ．∴ N（4，1）． ‎ ‎∵ 当时，y == 1，∴点N在函数 的图象上． ‎ ‎（3）4≤ m ≤8． ‎ ‎23．解：（1）4 5 6； ‎ ‎（2）不对． ‎ ‎∵OP = 2，PQ = 3，OQ = 4，且42≠32 + 22，即OQ2≠PQ2 + OP2，‎ ‎∴OP与PQ不垂直．∴PQ与⊙O不相切．‎ ‎（3）① 3； ‎ D H l O 图3‎ P Q ‎②由①知，在⊙O上存在点P，到l的距离为3，此时，OP将不能再向下转动，如图3．OP在绕点O左右摆动过程中所扫过的最大扇形就是OP．‎ 连结P，交OH于点D．‎ ‎∵PQ，均与l垂直，且PQ =，‎ ‎∴四边形PQ是矩形．∴OH⊥P，PD =D．‎ 由OP = 2，OD = OHHD = 1，得∠DOP = 60°．‎ ‎∴∠PO = 120°．‎ ‎∴ 所求最大圆心角的度数为120°．‎ ‎24．解：（1）AO = BD，AO⊥BD； ‎ 图4‎ A D O B C ‎2‎ ‎1‎ M N E F ‎（2）证明：如图4，过点B作BE∥CA交DO于E，∴∠ACO = ∠BEO．‎ ‎  又∵AO = OB，∠AOC = ∠BOE，‎ ‎∴△AOC ≌ △BOE．∴AC = BE． ‎ 又∵∠1 = 45°， ∴∠ACO = ∠BEO = 135°．‎ ‎∴∠DEB = 45°．‎ ‎∵∠2 = 45°，∴BE = BD，∠EBD = 90°．∴AC = BD． 延长AC交DB的延长线于F，如图4．∵BE∥AC，∴∠AFD = 90°．∴AC⊥BD．‎ ‎（3）如图5，过点B作BE∥CA交DO于E，∴∠BEO = ∠ACO．‎ 又∵∠BOE = ∠AOC ， ‎ A O B C ‎1‎ D ‎2‎ 图5‎ M N E ‎∴△BOE ∽ △AOC．‎ ‎∴． ‎ 又∵OB = kAO，‎ 由（2）的方法易得 BE = BD．∴． ‎ ‎25．解：（1）y = 2t；（2）当BP = 1时，有两种情形：‎ ‎①如图6，若点P从点M向点B运动，有 MB = = 4，MP = MQ = 3，‎ A D C B P M Q E 图6‎ ‎∴PQ = 6．连接EM，‎ ‎∵△EPQ是等边三角形，∴EM⊥PQ．∴．‎ ‎∵AB = ，∴点E在AD上．‎ ‎∴△EPQ与梯形ABCD重叠部分就是△EPQ，其面 积为． ‎ ‎②若点P从点B向点M运动，由题意得 ．‎ PQ = BM + MQBP = 8，PC = 7．设PE与AD交于点F，QE与AD或AD的 A D C B P M Q E F H G 图7‎ 延长线交于点G，过点P作PH⊥AD于点H，则 HP = ，AH = 1．在Rt△HPF中，∠HPF = 30°， ‎ ‎∴HF = 3，PF = 6．∴FG = FE = 2．又∵FD = 2，‎ ‎∴点G与点D重合，如图7．此时△EPQ与梯形ABCD ‎   的重叠部分就是梯形FPCG，其面积为．‎ ‎（3）能．4≤t≤5．‎ ‎26．解：（1）140 57500；‎ ‎（2）w内 = x（y -20）- 62500 = x2＋130 x，‎ w外 = x2＋（150）x．‎ ‎（3）当x = = 6500时，w内最大；分 由题意得 ， ‎ 解得a1 = 30，a2 = 270（不合题意，舍去）．所以 a = 30． ‎ ‎（4）当x  = 5000时，w内 = 337500， w外 =．‎ 若w内 ＜ w外，则a＜32.5；‎ 若w内 = w外，则a = 32.5；‎ 若w内 ＞ w外，则a＞32.5．‎ 所以，当10≤ a ＜32.5时，选择在国外销售；‎ 当a = 32.5时，在国外和国内销售都一样；‎ 当32.5＜ a ≤40时，选择在国内销售．‎