2020-2021学年沪科版九年级数学上册期中、期末考试模拟题及答案（各一套） 21页

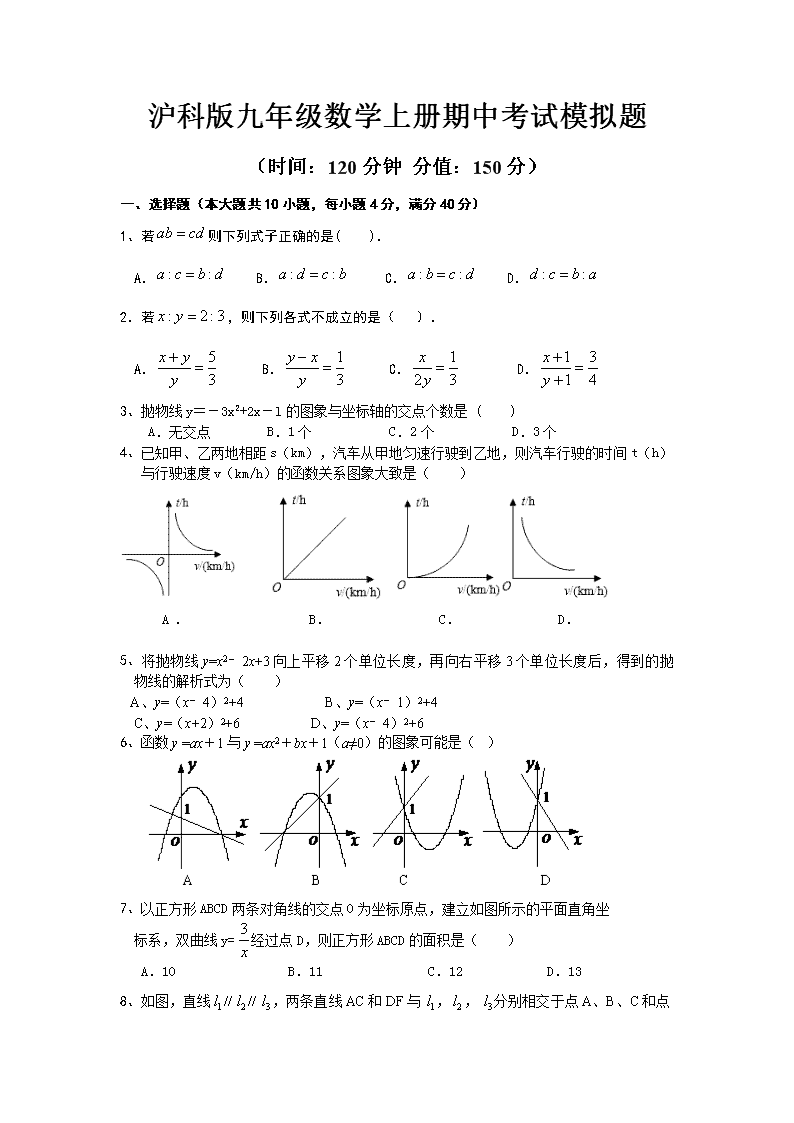
沪科版九年级数学上册期中考试模拟题 ‎（时间：120分钟 分值：150分）‎ 一、选择题（本大题共10小题，每小题4分，满分40分）‎ ‎1、若则下列式子正确的是( )． ‎ A． B． C． D．‎ ‎2．若，则下列各式不成立的是（ ）．‎ A． B． C． D．‎ ‎3、抛物线y＝－3x2+2x－l的图象与坐标轴的交点个数是 ( )‎ ‎ A．无交点 B．1个 C．2个 D．3个 ‎ ‎4、已知甲、乙两地相距s（km），汽车从甲地匀速行驶到乙地，则汽车行驶的时间t（h）与行驶速度v（km/h）的函数关系图象大致是（　　）‎ ‎ ‎ ‎ A . B． C． D． ‎ ‎5、将抛物线y=x2﹣2x+3向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式为（　　） ‎ ‎ A、y=（x﹣4）2+4 B、y=（x﹣1）2+4 ‎ C、y=（x+2）2+6 D、y=（x﹣4）2+6 ‎ ‎6、函数y =ax＋1与y =ax2＋bx＋1（a≠0）的图象可能是（ ）‎ ‎7、以正方形ABCD两条对角线的交点O为坐标原点，建立如图所示的平面直角坐 24‎ 标系，双曲线y=经过点D，则正方形ABCD的面积是（　　）  A．10 B．‎11 C．12 D．13j ‎8、如图，直线// // ，两条直线AC和DF与 ，， ‎ 分别相交于点A、B、C和点D、E、F．则下列比例式不正确的是（ ）．O ‎　‎ ‎ ‎ ‎ ‎ 第7题图 第8题图 第12题图 第13题图P ‎9、若方程的两个根是－3和1，那么二次函数的图象的对称轴是直线（ ）D ‎ A、＝－3 B、＝－‎2 C、＝－1 D、＝11‎ ‎10、如图，正方形ABCD的边长为3cm，动点P从B点出发以3cm/s的速 4‎ 度沿着边BC﹣CD﹣DA运动，到达A点停止运动；另一动点Q同时从e B点出发，以1cm/s的速度沿着边BA向A点运动，到达A点停止运动．设f P点运动时间为x（s），△BPQ的面积为y（cm2），则y关于x的函C 数图象是（　　） t ‎ ‎ ‎ C． ．4‎ ‎ A B C DR 二、填空题（本大题共4小题，每小题5分，满分20分）5‎ ‎11、若点 A ( 2, ) 在函数 的图像上，则 A 点的坐标是＿＿＿＿ ‎ ‎12、如图，△ABC中，点D、E分别在AB、AC上，且DE∥BC，若S△ADE=4，S△BDE=3，那么DE：BC=_____________．‎ ‎13、如图，∠ACD＝∠B，AC＝6，AD＝4，则AB＝________.‎ ‎14、抛物线y=ax2+bx+c（a≠0)的图象大致如图所示，下列说法：①2a+b=0; ②当-1≤x≤3时，y<0; ③若（x1，y1）、（x2，y2）在函数图象上，当x165时，‎ W随x的增大而减小，‎ ‎∴时，．‎ 因此，当该产品产量为‎75kg时获得的利润最大，最大利润是2250元………………………………………………………………………………………………4分 沪科版九年级数学上册期末考试模拟题 ‎（时间：120分钟 分值：150分）‎ 一、选择题（每小题4分，共40分）‎ ‎1．二次函数y=（x﹣1）2﹣3的最小值是（　　）‎ A．2 B．‎1 ‎C．﹣2 D．﹣3‎ ‎2．△ABC中，∠A，∠B均为锐角，且有|tan2B﹣3|+（2sinA﹣）2=0，则△ABC是（　　）‎ A．直角（不等腰）三角形 B．等边三角形 C．等腰（不等边）三角形 D．等腰直角三角形 ‎3．在反比例函数图象的每一支曲线上，y都随x的增大而减小，则k的取值范围是（　　）‎ A．k＜0 B．k＞‎0 ‎C．k＜1 D．k＞1‎ ‎4．如图，为了测量河岸A，B两点的距离，在与AB垂直的方向上取点C，测得AC=a，∠ABC=α，那么AB等于（　　）‎ A．a•sinα B．a•cosα C．a•tanα D．‎ ‎5．如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，若BD=2AD，则（　　）‎ A． B． C． D．‎ ‎6．把抛物线y=（x+1）2‎ 向下平移2个单位，再向右平移1个单位，所得到的抛物线是（　　）‎ A．y=（x+2）2+2 B．y=（x+2）2﹣‎2 ‎C．y=x2+2 D．y=x2﹣2‎ ‎7．将二次函数y=x2+x﹣1化为y=a（x+h）2+k的形式是（　　）‎ A．y= 　 B．y=（x﹣2）2﹣2 ‎ C．y=（x+2）2﹣2 　 D．y=（x﹣2）2+2‎ ‎8．若A（a1，b1），B（a2，b2）是反比例函数y=（x＞0）图象上的两个点，且a1＜a2，则b1与b2的大小关系是（　　）‎ A．b1＞b2 B．b1=b2 C．b1＜b2 D．大小不确定 ‎9．如图，某水库堤坝横断面迎水坡AB的斜面坡度是1：，堤坝高BC=‎50m，则迎水坡面AB的长度是（　　）‎ A．‎100m B．‎120m C．50m D．100m ‎10．如图，边长为的正方形ABCD的顶点A在y轴上，顶点D在反比例函数的图象上，已知点B的坐标是，则k的值为（　　）‎ A． B． C．4 D．6‎ 二、填空题（每小题5分，共20分）‎ ‎11．（5分）如图，若点A的坐标为，则sin∠1=　 　．‎ ‎12．（5分）如图，点A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点C、D在x轴上，且BC∥AD，四边形ABCD的面积为3，则这个反比例函数的解析式为　 　．‎ ‎13．（5分）如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是　 　．‎ ‎14．（5分）已知二次函数y=ax2+bx+c的图象如图所示，有以下结论：①a+b+c＜0；②a﹣b+c＞1；③abc＞0；④‎4a﹣2b+c＜0；⑤c﹣a＞1．其中所有正确结论的序号是　 　．‎ ‎　‎ 三、简答题（本大题共2小题，每小题8分，满分16分）‎ ‎15．（8分）求值： cos245°﹣sin30°tan60°+sin60°‎ ‎16．（8分）如图，△ABC的顶点坐标分别为A（1，3）、B（4，2）、C（2，1）．‎ ‎（1）作出与△ABC关于x轴对称的△A 1B‎1C1，并写出点A1的坐标；‎ ‎（2）以原点O 为位似中心，在原点的另一侧画出△A2B‎2C2，使=，并写出点A2的坐标．‎ ‎　‎ 四、简答题（本大题共2小题，每小题8分，满分16分）‎ ‎17．（8分）某国发生8.1级强烈地震，我国积极组织抢险队赴地震灾区参与抢险工作，如图，某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象，已知探测线与地面的夹角分别是25°和60°，且AB=‎4米，求该生命迹象所在位置C的深度．（结果精确到‎1米，参考数据：sin25°≈0.4，cos25°≈0.9，tan25°≈0.5，≈1.7）‎ ‎18．（8分）如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．‎ ‎（1）求证：△ADE∽△ABC；‎ ‎（2）若AD=3，AB=5，求的值．‎ ‎　‎ 五、简答题（本大题共2小题，每小题10分，满分20分）‎ ‎19．（10分）一种实验用轨道弹珠，在轨道上行驶5分钟后离开轨道，前2分钟其速度v（米/分）与时间t（分）满足二次函数v=at2，后三分钟其速度v（米/分）与时间t（分）满足反比例函数关系，如图，轨道旁边的测速仪测得弹珠1分钟末的速度为‎2米/分，求：‎ ‎（1）二次函数和反比例函数的关系式．‎ ‎（2）弹珠在轨道上行驶的最大速度．‎ ‎20．（10分）已知：如图，第一象限内的点A，B在反比例函数的图象上，点C在y轴上，BC∥x轴，点A的坐标为（2，4），且cot∠ACB=‎ 求：（1）反比例函数的解析式；‎ ‎（2）点C的坐标；‎ ‎（3）∠ABC的余弦值．‎ ‎　‎ 六、简答题（本题满分12分）‎ ‎21．（12分）甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在O点正上方‎1m的P处发出一球，羽毛球飞行的高度y（m）与水平距离x（m）之间满足函数表达式y=a（x﹣4）2+h，已知点O与球网的水平距离为‎5m，球网的高度为‎1.55m．‎ ‎（1）当a=﹣时，①求h的值；②通过计算判断此球能否过网．‎ ‎（2）若甲发球过网后，羽毛球飞行到与点O的水平距离为‎7m，离地面的高度为m的Q处时，乙扣球成功，求a的值．‎ ‎　‎ 七、（本题满分12分）‎ ‎22．（12分）已知：如图，有一块面积等于‎1200cm2的三角形纸片ABC，已知底边与底边BC上的高的和为‎100cm（底边BC大于底边上的高），要把它加工成一个正方形纸片，使正方形的一边EF在边BC上，顶点D、G分别在边AB、AC上，求加工成的正方形铁片DEFG的边长．‎ ‎　‎ 八、（本题满分14分）‎ ‎23．（14分）如图，在平面直角坐标系中，已知点A（10，0），B（4，8），C（0，8），连接AB，BC，点P在x轴上，从原点O出发，以每秒1个单位长度的速度向点A运动，同时点M从点A出发，以每秒2个单位长度的速度沿折线A﹣B﹣C向点C运动，其中一点到达终点时，另一点也随之停止运动，设P，M两点运动的时间为t秒．‎ ‎（1）求AB长；‎ ‎（2）设△PAM的面积为S，当0≤t≤5时，求S与t的函数关系式，并指出S取最大值时，点P的位置；‎ ‎（3）t为何值时，△APM为直角三角形？‎ ‎　‎ 参考答案 ‎1．D；2．B；3．D；4．D；5．B；6．D；7．C；8．A；9．A；10．C；　‎ ‎11．；12．y=﹣；13．x＜﹣1或x＞5；14．①②③⑤；‎