【40套试卷合集】河南省鹤壁市名校2019-2020学年数学九上期末模拟试卷含答案 10页

‎2019-2020 学年九上数学期末模拟试卷含答案 一、单选题（共 10 题；共 30 分）‎ x ‎1. 某车的刹车距离 y（ m）与开始刹车时的速度 x（ m/s ）之间满足二次函数 y= 2（ x＞ 0），若该车某次 的刹车距离为 5m，则开始刹车时的速度为（ ）‎ A. 40 m/s B. 20 m/s C. 10 m/s D. 5 m/s ‎2. 下列一元二次方程中，有两个不相等的实数根的方程是（ ）‎ x A. B. C. D. 3. 用公式法解一元二次方程 2﹣ 5x=6，解是（ ）‎ A. x1=3， x2=2 B. x1=﹣ 6， x2=﹣ 1 C. x1=6， x2=﹣ 1 D. x1=﹣ 3， x2=﹣ 2 4. 用配方法解方程 时，经过配方，得到（ ）‎ A. B. C. D.‎ ‎2‎ ‎5. 如图，是二次函数 y=ax +bx+c 图象的一部分，其对称轴为直线 x=1，若其与 x 轴交于点为 A（ 3，0），则 由图象可知，方程 ax2+bx+c 的另一个解是（ ）‎ A. ﹣ 1 B﹣.‎ ‎2 C﹣.‎ ‎1.5 D.﹣ 2.5‎ ‎6. △ ABC中， AB=12，BC=18，CA=24，另一个和它相似的三角形最长的一边是 36，则最短的一边是（ ）‎ A. 27 B. 12 C. 18 D. 20‎ ‎2‎ ‎7. 如图，抛物线 y=ax +bx+c（ a≠0）的对称轴为直线 x=1，与 x 轴的一个交点坐标为（﹣ 1， 0），其部分图 象如图所示，下列结论：‎ ‎2‎ ‎① 4ac ＜ b ；‎ ‎2‎ ‎② 方程 ax +bx+c=0 的两个根是 x1=﹣ 1， x2=3；‎ ‎③ 3a+c ＞0‎ ‎④ 当 y＞ 0 时， x 的取值范围是﹣ 1≤x＜ 3‎ ‎⑤ 当 x＜ 0 时， y 随 x 增大而增大 其中结论正确的个数是（ ）‎ A. 4 个 B. 3个 C. 2个 D. 1个 ‎2‎ ‎8. 关于 x 的方程 x +kx﹣ 1=0 的根的情况是（ ）‎ A. 有两个不相等的实数根 B.有两个相等的实数根 C.只有一个实数根 D. 没有实数根 ‎9. 已知一元二次方程 x ‎2﹣ 3x﹣3=0 的两根为 α与 β，则 的值为（ ）‎ A. -1 B. 1 C. -2 D. 2‎ ‎10.下列方程中，是关于 x 的一元二次方程的是（ ）‎ A. 3（ x+1）‎ ‎2 2‎ ‎=2（ x+1） B. + ﹣ 2=0 C. ax+bx+c=0 D. 2x+1=0‎ 二、填空题（共 8 题；共 24 分）‎ ‎12.用一根长为 32cm 的铁丝围成一个矩形，则围成的矩形面积的最大值是 ‎2‎ ‎ cm ．‎ ‎13.某种物品经过两次降价，其价格为降价前的 81%，则平均每次降价的百分数为 ‎ ‎2‎ ‎14.把抛物线 y=x -4x+5 的图象向右平移 3 个单位，再向下平移 2 个单位，所得图象的解析式是 ‎ ‎15.已知：如图，在 △ABC 中，∠ ACB=90°， CD⊥ AB，垂足是 D， BC= ， BD=1．求 AD= ‎ ‎16.计算 ﹣ 的结果是 ．‎ ‎17.如果两个相似三角形周长的比是 23，那么它们面积的比是 .‎ ‎18. 如图，在 Rt△ ABC 中，∠ ACB=90°， CD⊥ AB，垂足为 D， tan∠ ACD= ， AB=5，那么 CD 的长是 ‎ ．‎ 三、解答题（共 6 题；共 36 分）‎ ‎19.甲、乙、丙三位同学进行足球传球训练，球从一个人脚下随机传到另一个人脚下，且每位传球人传给 其余两人的机会是均等的，由甲开始传球，共传三次．‎ ‎（ 1）求三次传球后，球回到甲脚下的概率；‎ ‎（ 2）三次传球后，球回到甲脚下的概率大还是传到乙脚下的概率大？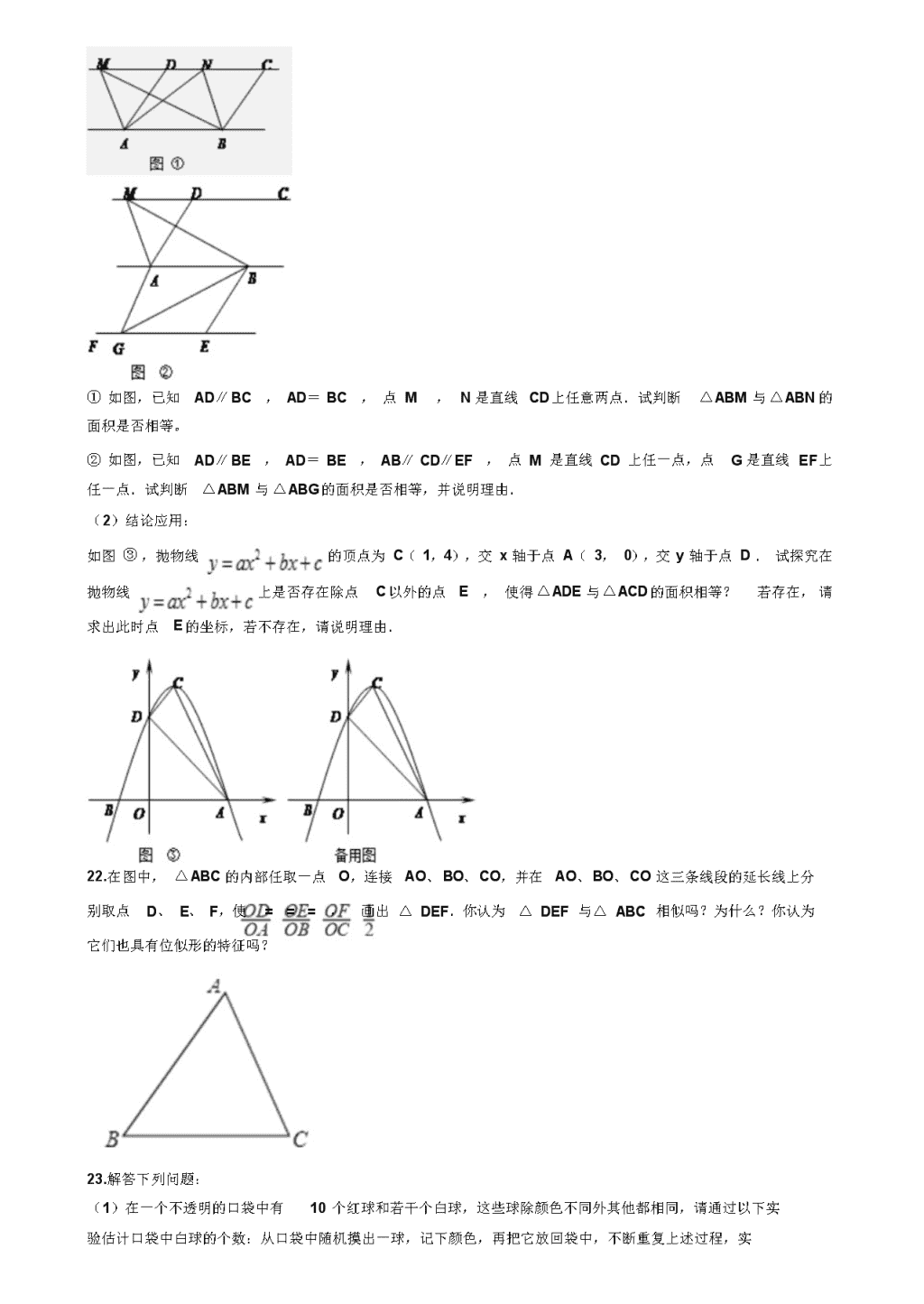‎ ‎20.如图， △ ABC中， D 为 AB 上一点．已知 △ ADC 与 △ DBC的面积比为 1： 3，且 AD=3，AC=6，请求出 BD 的长度，并完整说明为何∠ ACD=∠ B 的理由．‎ ‎21. （ 1）探究新知：‎ ‎① 如图，已知 AD∥ BC ， AD＝ BC ， 点 M ， N 是直线 CD 上任意两点．试判断 △ ABM 与 △ ABN 的 面积是否相等。‎ ‎② 如图，已知 AD∥ BE ， AD＝ BE ， AB∥ CD∥ EF ， 点 M 是直线 CD 上任一点，点 G 是直线 EF上 任一点．试判断 △ ABM 与 △ ABG的面积是否相等，并说明理由．‎ ‎（ 2）结论应用：‎ 如图 ③ ，抛物线 的顶点为 C（ 1，4），交 x 轴于点 A（ 3， 0），交 y 轴于点 D ． 试探究在 抛物线 上是否存在除点 C 以外的点 E ， 使得 △ ADE 与 △ ACD的面积相等？ 若存在， 请 求出此时点 E 的坐标，若不存在，请说明理由．‎ ‎22.在图中， △ ABC 的内部任取一点 O，连接 AO、 BO、 CO，并在 AO、 BO、 CO 这三条线段的延长线上分 别取点 D、 E、 F，使 = = = ， 画出 △ DEF．你认为 △ DEF 与△ ABC 相似吗？为什么？你认为 它们也具有位似形的特征吗？‎ ‎23.解答下列问题：‎ ‎（ 1）在一个不透明的口袋中有 10 个红球和若干个白球，这些球除颜色不同外其他都相同，请通过以下实 验估计口袋中白球的个数：从口袋中随机摸出一球，记下颜色，再把它放回袋中，不断重复上述过程，实 验总共摸了 200 次，其中有 50 次摸到了红球，那么估计口袋中有白球多少个？‎ ‎（ 2）请思考并作答： 在一个不透明的口袋里装有若干个形状、大小完全相同的白球，在不允许将球倒出来的情况下，如何估计 白球的个数（可以借助其它工具及用品）？写出解决问题的主要步骤及估算方法，并求出结果（其中所需 数量用 a、 b、 c 等字母表示） ．‎ ‎24.如图，某日在我国某岛附近海域有两艘自西向东航行的海监船 A、 B，船在 A 船的正东方向，且两船保 持 20 海里的距离， 某一时刻两海监船同时测得在 A 的东北方向， 的北偏东 15°方向有一我国渔政执法船 C， 求此时船 C与船 B 的距离是多少． （结果保留小数点后一位）‎ 参考数据： ≈1.414， ≈1.732， ≈2.236．‎ 四、综合题（共 10 分）‎ ‎25.如图所示， 某工程队准备在山坡 （山坡视为直线 l）上修一条路， 需要测量山坡的坡度， 即 tan α的值．测 量员在山坡 P 处（不计此人身高）观察对面山顶上的一座铁塔，测得塔尖 C 的仰角为 31°，塔底 B 的仰角 为 26.6 °．已知塔高 BC=40米，塔所在的山高 OB=240 米， OA=300 米，图中的点 O、 B、C、A、P 在同一平 面内．‎ 求：‎ ‎（ 1） P 到 OC 的距离．‎ ‎（ 2）山坡的坡度 tan α．‎ ‎（参考数据 sin26.6 °≈ 0，.45tan26.6 °≈ 0.；50sin31 °≈ 0.，52tan37°≈ 0.）60‎ 参考答案与试题解析 一、单选题 ‎1. 【答案】 C ‎【考点】二次函数的应用 ‎【解析】【分析】本题实际是告知函数值求自变量的值，代入求解即可．另外实际问题中，负值舍去．‎ ‎【解答】当刹车距离为 5m 时， 即 y=5，代入二次函数解析式：‎ ‎2‎ ‎5= x ．‎ 解得 x=±10，（ x=-10 舍去 )， 故开始刹车时的速度为 10m/s ． 故选 C．‎ ‎【点评】 考查自变量的值与函数值的一一对应关系， 明确 x、y 代表的实际意义， 刹车距离为 5m ，即是 y=5， 求刹车时的速度 x．‎ ‎2. 【答案】 A ‎【考点】根的判别式 ‎【解析】【分析】计算出各项中方程根的判别式的值，找出大于 0 的选项即可．‎ A、这里 a=1， b=-3， c=1，‎ ‎∵△ =b2-4ac=5＞0，‎ ‎∴方程有两个不相等的实数根，本选项符合题意；‎ B、这里 a=1， b=0， c=1，‎ ‎∵△ =b2-4ac=-4＜ 0，‎ ‎∴方程没有实数根，本选项不合题意；‎ C、这里 a=1， b=-2， c=1，‎ ‎∵△ =b2-4ac=0，‎ ‎∴方程有两个相等的实数根，本选项不合题意；‎ D、这里 a=1， b=2，c=3，‎ ‎∵△ =b2-4ac=-5＜ 0，‎ ‎∴方程没有实数根，本选项不合题意； 故选 A.‎ ‎3. 【答案】 C ‎【考点】解一元二次方程 -公式法 ‎【解析】【解答】解：∵ x2﹣ 5x=6‎ ‎∴ x2﹣ 5x﹣ 6=0‎ ‎∵ a=1， b=﹣ 5， c=﹣ 6‎ ‎∴ b2﹣ 4ac=（﹣ 5） 2﹣ 4×1×（﹣ 6） =49‎ ‎∴ x=‎ ‎∴ x1=6， x2=﹣ 1． 故选 C．‎ ‎【分析】运用公式法，首先确定 a， b， c 的值，然后判断方程是否有解，如有解代入公式即可求解．‎ ‎4. 【答案】 D ‎【考点】解一元二次方程 -配方法 ‎【解析】【分析】把方程 x2 2‎ ‎+4x+1=0，的常数项移到等号的右边，得到 x ‎+4x+4=-1+4‎ 方程两边同时加上一次项系数一半的平方，得到 x2‎ ‎+4x=-1，‎ 配方得（ x+2）‎ ‎2‎ ‎=3．‎ 故答案是： D．‎ ‎5. 【答案】 A ‎【考点】抛物线与 x 轴的交点 ‎【解析】【解答】解：由抛物线的对称性得：抛物线的与 x 轴另一个交点为（﹣ 1， 0）， ∴方程 ax2+bx+c 的另一个解为： x=﹣ 1， 故选 A．‎ ‎【分析】根据图象得：抛物线与 x 轴的另一个交点为（﹣ 1， 0），从而得出方程的另一个解． 6. 【答案】 C ‎【考点】相似三角形的性质 ‎【解析】解答：设另一个三角形最短的一边是 x ， ∵△ ABC中， AB=12，BC=18，CA=24，另一个和它相 似的三角形最长的一边是 36，‎ ‎∴ ，‎ 解得 x=18． 故选 C．‎ 分析：设另一个三角形最短的一边是 x ， 根据相似三角形对应边成比例即可得出结论．‎ ‎7. 【答案】 B ‎【考点】二次函数的性质，二次函数图象与系数的关系 ‎【解析】【解答】∵抛物线与 x 轴有 2 个交点，‎ ‎∴ b2﹣ 4ac＞ 0，所以 ① 正确；‎ ‎∵抛物线的对称轴为直线 x=1，‎ 而点（﹣ 1， 0）关于直线 x=1 的对称点的坐标为（ 3， 0），‎ ‎∴方程 ax2+bx+c=0 的两个根是 x =﹣ 1， x =3，所以 ② 正确；‎ ‎1 2‎ ‎∵ x=﹣ =1，即 b=﹣ 2a ，‎ 而 x=﹣ 1 时， y=0，即 a﹣ b+c=0，‎ ‎∴ a+2a+c=0，所以 ③ 错误；‎ ‎∵抛物线与 x 轴的两点坐标为（﹣ 1， 0），（3， 0），‎ ‎∴当﹣ 1＜ x＜ 3 时， y＞ 0，所以 ④ 错误；‎ ‎∵抛物线的对称轴为直线 x=1，‎ ‎∴当 x＜ 1 时， y 随 x 增大而增大，所以 ⑤ 正确． 故答案为： B．‎ ‎【分析】 ① 由图像可知抛物线与 x 轴有 2 个交点，即 b2﹣ 4ac＞ 0，由此可以判断 ① 的正误；‎ ‎② 由图像可知抛物线的对称轴为直线 x=1，根据点关于线对称的性质可知抛物线与 x 轴的另一交点为 3； 从而可以判断 ② 的正误；‎ ‎③ 由对称轴的公式可得 b=﹣ 2a，由图像可知 a﹣ b+c=0，从而可以判断 ③ 的正误；‎ ‎④ 由二次函数图像和性质可知当﹣ 1＜ x＜ 3 时， y＞ 0，由此可判断 ④ 的正误；‎ ‎⑤ 根据二次函数的性质可知对当 x＜ 1 时， y 随 x 增大而增大，由此可判断 ⑤ 的正误 . 8. 【答案】 A ‎【考点】根的判别式 ‎【解析】【解答】解：∵△ =k ‎2‎ ‎+4＞ 0，∴方程有两个不相等的实数根．‎ 故选 A．‎ ‎【分析】求出 △的值即可得出结论．‎ ‎9. 【答案】 A ‎【考点】根与系数的关系 ‎【解析】【解答】解：根据题意得 α+β=，3 αβ﹣=3， 所以 =﹣ 1．‎ 故选 A．‎ ‎【分析】先根据根与系数的关系得到 α+β=，3 αβ﹣=3，再通分得到 ， 然后利用整体代 入的方法计算．‎ ‎10.【答案】 A ‎【考点】一元二次方程的定义 ‎【解析】【解答】解： A、是一元二次方程，故本选项正确； B、不是一元二次方程，故本选项错误； C、不是一元二次方程，故本选项错误；‎ D、不是一元二次方程，故本选项错误；‎ 故选 A．‎ ‎【分析】只含有一个未知数，并且所含未知数的项的最高次数是 2 的整式方程叫一元二次方程，根据以上 定义判断即可．‎ 二、填空题 ‎11.【答案】 5‎ ‎【考点】解直角三角形的应用 -仰角俯角问题 ‎【解析】【解答】解：设 DB=xm， 在 Rt△ ADB 中， AB=xtan60°= xm，‎ 在 Rt△ ACB中， =tan30°，‎ 整理得， = ，‎ 解得， 3x=x+10， x=5，‎ 则 AB=5 m． 故答案为 5 ．‎ ‎【分析】设 DB=xm，在 Rt△ ADB 中，得到 AB=xtan60°= xm，再在 Rt△ACB 中，得到 =tan30°，据 此即可解答．‎ ‎12.【答案】 64‎ ‎【考点】一元二次方程的应用 ‎【解析】【解答】解：设矩形的一边长是 xcm，则邻边的长是（ 16-x） cm． 则矩形的面积 S=x(16-x)，‎ 即 S=-x2+16x ， S=-(x-8)2+64．‎ 当 x=8 时， S 有最大值 64． 故答案为 64.‎ ‎【分析】设矩形的一边长是 xcm，则邻边的长是（ 16-x） cm．则写出 S 与 x 的关系式，是一个二次函数， 求其最值即可 .‎ ‎13.【答案】 10%‎ ‎【考点】一元二次方程的应用 ‎=81%，‎ ‎【解析】【解答】解：设平均每次降价的百分数为 x， 根据题意得： （1﹣ x） 2‎ 开方得： 1﹣ x=0.9 或 1﹣ x=﹣ 0.9 ， 解得： x1=0.1=10%， x2=1.9， 则平均每次降价得百分数为 10%． 故答案为： 10%．‎ ‎【分析】设平均每次降价的百分数为 x，根据题意列出方程，求出方程的解即可得到结果．‎ ‎2‎ ‎14.【答案】 y=x -10x+24‎ ‎【考点】二次函数图象与几何变换 ‎-4x+5=（‎ ‎【解析】【解答】 y=x2‎ ‎x-2）‎ ‎2‎ ‎+1，‎ 由 “左加右减 ”的原则可知， 抛物线 y=（ x-2）‎ ‎2‎ ‎+1 的图象向右平移 3 个单位所得函数图象的关系式是： y=（ x-5）‎ ‎2‎ ‎+1；‎ ‎2‎ 由 “上加下减 ”的原则可知， 抛物线 y=（ x-5） +1 的图象向下平移 2 个单位所得函数图象的关系式是： y=（ x-5）‎ ‎2‎ ‎-1，‎ 即 y=x ‎2‎ ‎-10x+24．‎ ‎-4x+5 写成顶点式，再根据 ‎【分析】先利用配方法将抛物线 y=x2‎ ‎‎ ‎“上加下减，左加右减 ‎‎ ‎”的原则进行解答即 可．‎ ‎15.【答案】 5‎ ‎【考点】相似三角形的判定与性质 ‎=BD?BA，‎ ‎【解析】【解答】解：由射影定理得， BC2‎ 则 BA=6，‎ ‎∴ AD=BA﹣ BD=5，‎ 故答案为： 5．‎ ‎【分析】根据射影定理列出等积式，把已知数据代入计算即可．‎ ‎16.【答案】 2‎ ‎【考点】二次根式的加减法 ‎【解析】【解答】解：原式 =3 ﹣ =2 ， 故答案为： 2‎ ‎【分析】原式各项化简后，合并即可得到结果．‎ ‎17.【答案】 49‎ ‎【考点】相似三角形的性质 ‎【解析】【解答】‎ ‎∵两个相似三角形周长的比是 2： 3，‎ ‎∴它们的相似比是 2： 3；‎ ‎∴它们的面积比为 4： 9．‎ ‎【分析】相似三角形的性质．相似三角形的周长比等于相似比，而面积比等于相似比的平方，由此得解 . 18.【答案】‎ ‎【考点】解直角三角形 ‎【解析】【解答】解：∵∠ ACB=9°0 ， CD⊥ AB， ∴∠ ACD+∠ BCD=∠ BCD+∠ B=90°，‎ ‎∴∠ B=∠ ACD，‎ ‎∵ tan∠ ACD= ，‎ ‎∴ tan∠ B= = ， 设 AC=3x， BC=4x，‎ ‎∵ AC2 2 2‎ ‎+BC =AB ，‎ ‎∴（ 3x） 2 +（ 4x） 2 2‎ ‎=5 ，‎ 解得： x=1，‎ ‎∴ AC=3， BC=4，‎ ‎∵ S△ ABC= ，‎ ‎∴ CD= = ，‎ 故答案为： ．‎ ‎【分析】根据余角的性质得到∠ B=∠ ACD，由 tan∠ ACD= ，得到 tan∠ B= = ，设 AC=3x，BC=4x， 根据勾股定理得到 AC=3， BC=4，根据三角形的面积公式即可得到结论． ．‎ 三、解答题 ‎19.【答案】（ 1）解：根据题意画出树状图如下：‎ 由树形图可知三次传球有 8 种等可能结果； 三次传球后，球回到甲脚下的概率 = = ；‎ ‎（ 2）由（ 1）可知球回到乙脚下的概率 = ， 所以球回到乙脚下的概率大．‎ ‎【考点】列表法与树状图法 ‎【解析】【分析】（ 1）画出树状图，根据树形图，利用概率公式列式求出球回到甲脚下的概率即可得解；‎ ‎（ 2）计算出传到乙脚下的概率，比较大小即可．‎ ‎20.【答案】解：∵△ ADC 与 △ DBC同高，且 △ ADC与 △ DBC的面积比为 1： 3， AD=3，‎ ‎∴ BD=9，‎ ‎∴ AB=12，‎ ‎∵ AC=6，‎ ‎∴‎ ‎∵∠ A=∠ A，‎ ‎∴△ ADC∽△ ACB，‎ ‎∴∠ ACD=∠ B．‎ ‎【考点】相似三角形的判定与性质 ‎【解析】【分析】由于 △ ADC 与 △ DBC 同高，且 △ ADC 与△ DBC 的面积比为 1： 3， AD=3，可求出 BD=9， 推得 AB=12，有相似三角形的判定证得 △ ADC∽△ ACB，再由相似三角形的判定可推得结论．本题主要考 查了三角形的面积，相似三角形的判定和性质，灵活应用相似三角形的判定和性质是解决问题的关键．‎ ‎21.【答案】﹙ 1﹚相等 ‎② 相 等 ． 理 由 如 下 ： 分 别 过 点 D ， E 作 DH⊥ AB ， E⊥ AB ， 垂 足 分 别 为 H ， ．‎ 则∠ DHA＝∠ EB＝90°．∵ AD∥ BE ， ∴∠ DAH＝∠ EB ． ∵ AD＝ BE ，‎ ‎∴△ DAH≌△ EB ． ∴ DH＝ E ． ∵ CD∥ AB∥ EF ，‎ ‎∴ S△ ABM＝ ， S△ ABG＝ ， ∴ S△ ABM＝ S△ ABG.‎ ‎﹙ 2﹚答：存在．‎ 解：因为抛物线的顶点坐标是 C(1， 4)，所以，可设抛物线的表达式为 .‎ 又因为抛物线经过点 A(3， 0)，将其坐标代入上式，得 ， 解得 .‎ ‎∴ 该抛物线的表达式为 ， 即 ．‎ ‎∴ D 点坐标为（ 0， 3）．‎ 设直线 AD 的表达式为 ， 代入点 A 的坐标，得 ， 解得 .‎ ‎∴ 直线 AD 的表达式为 ．‎ 过 C 点作 CG⊥ x 轴，垂足为 G ， 交 AD 于点 H ． 则 H 点的纵坐标为 ．‎ ‎∴ CH＝ CG－ HG＝ 4－ 2＝ 2．‎ 设点 E 的横坐标为 m ， 则点 E的纵坐标为 ．‎ 过 E 点作 EF⊥ x 轴，垂足为 F ， 交 AD 于点 P ， 则点 P 的纵坐标为 ， EF∥ CG ．‎