2013年四川省南充市中考数学试题（含答案） 11页

‎2013四川南充中考数学试题 ‎（满分100分，考试时间90分钟）‎ 一、选择题（本大题共10小题，每小题3分，共30分）‎ ‎1. （2013四川南充，1，3分）计算－2+3的结果是 （ ）‎ A.－5 B. 1 C.-1 D. 5‎ ‎2. （2013四川南充，2，3分）0.49的算术平方根的相反数是 （ ）‎ A.0.7 B. －0.7 C. D. 0‎ ‎3. （2013四川南充，3，3分） 如图，△ABC中，AB=AC,∠B=70°，则∠A的度数是（ ）‎ A B C 第3题目题目题同，题 A.70° B. 55° C. 50° D. 40° ‎ ‎4. （2013四川南充，4，3分）“一方有难，八方支援。”2013年4月20日四川省芦山县遭遇强烈地震灾害，我市某校师生共同为地震灾区捐款135000元用于灾后重建，把135000用科学记数法表示为 （ ）‎ A.1.35×10 B. 13.5×10 ‎ C. 1.35×10 D. 13.5×10‎ ‎5. （2013四川南充，5，3分）不等式组的整数解是（ ）‎ A.－1，0,1 B. 0,1 ‎ ‎ C. －2，0,1 D. －1,1 ‎ ‎6. 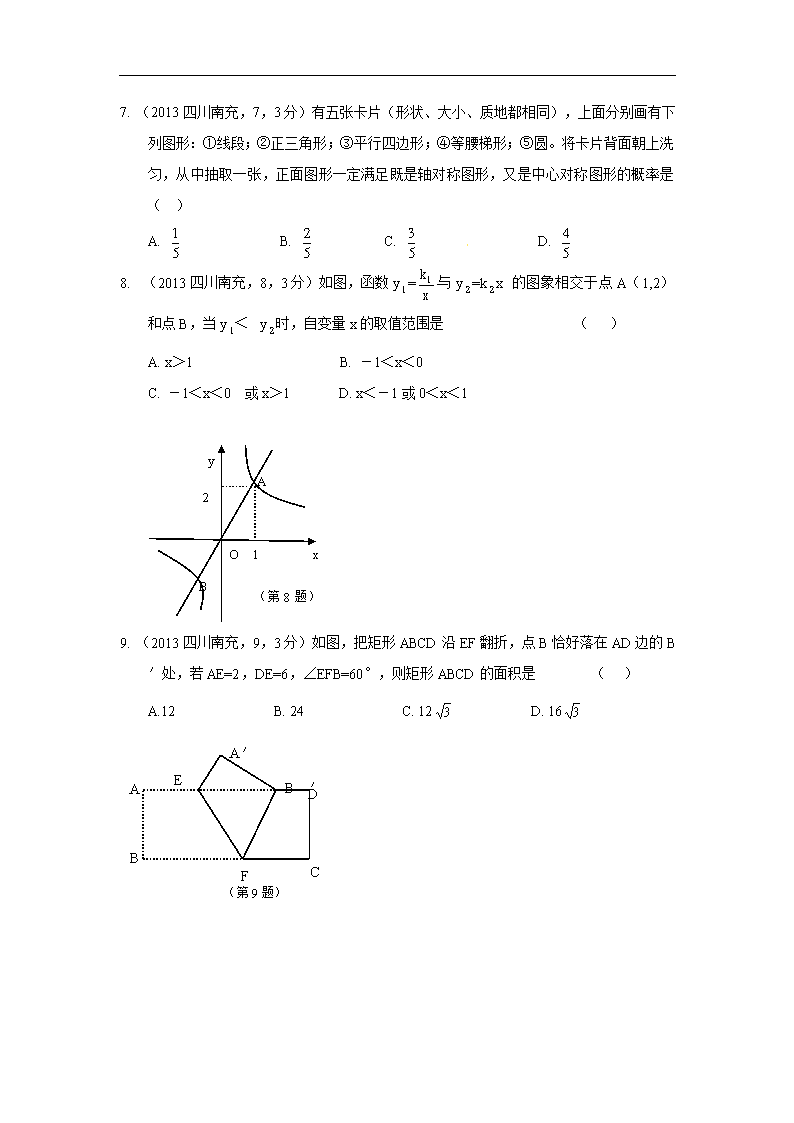（2013四川南充，6，3分） 下列图形中，∠2＞∠1 （ ）‎ ‎1词 ‎21‎ A ‎ ‎1 ‎ ‎（平行四边形） ‎ B ‎ ‎2 ‎ C ‎ ‎2 ‎ ‎1 ‎ D ‎ a ‎ b ‎ ‎(a∥b) ‎ ‎ 第6题 ‎7. （2013四川南充，7，3分）有五张卡片（形状、大小、质地都相同），上面分别画有下列图形：①线段；②正三角形；③平行四边形；④等腰梯形；⑤圆。将卡片背面朝上洗匀，从中抽取一张，正面图形一定满足既是轴对称图形，又是中心对称图形的概率是 （ ）‎ A. B. C. D. ‎ ‎8. （2013四川南充，8，3分）如图，函数y=与 y=kx 的图象相交于点A（1,2）和点B，当y＜ y时，自变量x的取值范围是 （ ）‎ A. x＞1 B. －1＜x＜0 ‎ C. －1＜x＜0 或x＞1 D. x＜－1或0＜x＜1‎ O ‎ A y ‎ B ‎1‎ ‎2‎ xz ‎（第8题）‎ ‎9. （2013四川南充，9，3分）如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE=2，DE=6，∠EFB=60°，则矩形ABCD的面积是 （ ）‎ A.12 B. 24 C. 12 D. 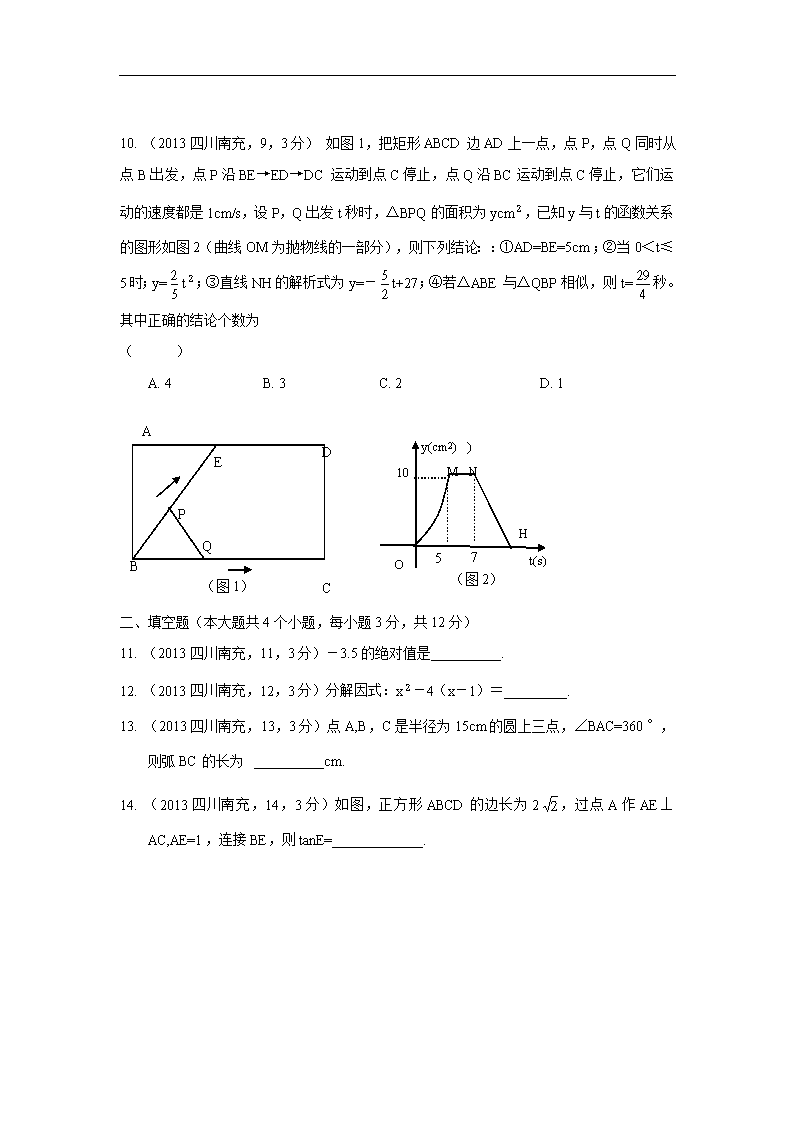16‎ A B A′‎ E F B′‎ C D ‎（第9题）‎ ‎10. （2013四川南充，9，3分） 如图1，把矩形ABCD边AD上一点，点P，点Q同时从点B出发，点P沿BE→ED→DC 运动到点C停止，点Q沿BC运动到点C停止，它们运动的速度都是1cm/s，设P，Q出发t秒时，△BPQ的面积为ycm，已知y与t的函数关系的图形如图2（曲线OM为抛物线的一部分），则下列结论：：①AD=BE=5cm；②当0＜t≤5时；y=t；③直线NH的解析式为y=－t+27；④若△ABE与△QBP相似，则t=秒。其中正确的结论个数为 （ ）‎ A. 4 B. 3 C. 2 D. 1‎ C D ‎（图1）‎ B A E Q P ‎ ‎y(cm2))‎ ‎（图2）‎ M ‎10‎ O N H ‎5‎ ‎7‎ t(s))‎ 二、填空题（本大题共4个小题，每小题3分，共12分）‎ ‎11. （2013四川南充，11，3分）－3.5的绝对值是__________.‎ ‎12. （2013四川南充，12，3分）分解因式：x－4（x－1）＝_________.‎ ‎13. （2013四川南充，13，3分）点A,B，C是半径为15cm的圆上三点，∠BAC=360°，则弧BC的长为__________cm.‎ ‎14. （2013四川南充，14，3分）如图，正方形ABCD的边长为2，过点A作AE⊥AC,AE=1，连接BE，则tanE=_____________.‎ A B C D E ‎(第14题)‎ 三、（本大题共3个小题，每小题6分，共18分）‎ ‎15. （2013四川南充，15，6分）计算（－1）+（2sin30°+）－+（）‎ ‎16. （2013四川南充，15，6分） 如图，在平行四边形ABCD中，对角线AC,BD交于点O,经过点O的直线交AB于E，交CD于F.‎ 求证：OE=OF.‎ A B C D E F O ‎17. （2013四川南充，17，6分）某校九年级有1200名学生，在体育考试前随机抽取部分学生进行体能测试，成绩分别记为A、B、C、D共四个等级，其中Ａ级和Ｂ级成绩为“优”，将测试结果绘制成如下条形统计图和扇形统计图．‎ A ‎ BA ‎ CA ‎ DA ‎ 人数 ‎ 等级A ‎ 成绩频数条形统计图 ‎ ‎30% 别 ‎ ‎ A级 ‎ ‎20% 别 ‎ ‎ C级 ‎ B级 ‎ D级 ‎ 成绩频数扇形统计图 ‎ ‎ ‎ ‎（1）求抽取参加体能测试的学生人数；‎ ‎（２）估计该校九年级全体学生参加体能测试成绩为“优”的学生共有多少人？‎ ‎ ‎ 四、（本大题有2小题，每小题8分，共16分）‎ ‎18. （2013四川南充，18，8分）某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y（件）之间满足如图所示的关系：‎ ‎（1）求出y与x之间的函数关系式；‎ ‎（2）写出每天的利润W与销售单价x之间的函数关系式；若你是商场负责人，会将售价定为多少，来保证每天获得的利润最大，最大利润是多少？‎ y(件) ‎ x(元/件) ‎ ‎30 ‎ ‎50 ‎ ‎130 ‎ ‎150 ‎ O ‎ ‎19. （2013四川南充，19，8分）如图，等腰梯形ABCD中，AD∥BC，AD＝3，BC＝7，∠B＝60°，P为BC边上一点（不与B，C重合），过点P作∠APE＝∠B，PE交CD 于E.‎ ‎(1)求证:△APB∽△PEC;‎ ‎(2)若CE＝3,求BP的长.‎ A ‎ B ‎ D ‎ CB ‎ PB ‎ E ‎ 五、（满分8分）‎ ‎20. （2013四川南充，20，8分）关于x的一元二次方程为（ｍ－1）x2－2ｍx＋ｍ＋1＝0‎ ‎（1）求出方程的根；‎ ‎（2）ｍ为何整数时，此方程的两个根都为正整数？‎ 六、（满分8分）‎ ‎21．（2013四川南充，21，8分）如图，公路AB为东西走向，在点A北偏东36.5°方向上，距离5千米处是村庄M；在点A北偏东53.5°方向上，距离10千米处是村庄N（参考数据：sin36.5°＝0.6，cos36.5°＝0.8，tan36.5°＝0.75）.‎ ‎（1）求M，N两村之间的距离；‎ ‎（2）要在公路AB旁修建一个土特产收购站P，使得M，N两村到P站的距离之和最短，求这个最短距离。‎ 北A A ‎ N ‎ M ‎ B ‎ 七、（满分8分）‎ ‎22．（2013四川南充，21，8分）如图，二次函数y=x2+bx－3b+3的图象与x轴交于A、B两点（点A在点B的左边），交y轴于点C，且经过点（b－2，2b2－5b－1）.‎ ‎（1）求这条抛物线的解析式；‎ ‎（2）⊙M过A、B、C三点，交y轴于另一点D，求点M的坐标；‎ ‎（3）连接AM、DM，将∠AMD绕点M顺时针旋转，两边MA、MD与x轴、y轴分别交于点E、F，若△DMF为等腰三角形，求点E的坐标.‎ 参考答案 一、选择题（本大题共10个小题，每小题3分，共30分）‎ ‎1.B 2.B 3.D 4.C 5.A 6.C 7.B 8.C 9.D 10.B ‎ 二、填空题（本大题共4个小题，每小题3分，共12分）‎ ‎11.3.5 ；12.（x－2）； 13. 6π；14. .‎ 三、（本大题共3个小题，每小题6分，共18分）‎ ‎15.解：原式=－1+1－2+3 ……………4′ ‎ ‎ =1 ……………6′ ‎ ‎16.证明：∵四边形ABCD是平行四边形，‎ ‎∴OA=OC,AB∥CD ……………2′‎ ‎∴∠OAE=∠OCF ……………3′‎ ‎∵∠AOE=∠COF ……………5′‎ ‎∴△OAE≌△OCF（ASA） ‎ ‎∴OE=OF ……………6′‎ ‎17.解：（1）参加体能测试的学生人数为60÷30%=200（人）……………2′‎ ‎（2）C级人数为200×20%=40（人）……………3′‎ ‎∴B级人数为200－60－15－40=85（人）……………4′‎ ‎∴“优”生共有人数为1200×=870（人）……………6′‎ 四、（本大题共2个小题，每小题8分，共16分）‎ ‎18.解：（1）设y与x之间的函数关系式为y＝kx＋b（k≠0）.由所给函数图象得 ‎ ……………1′‎ ‎ ……………2′解得 ……………3′ ‎ ‎∴函数关系式为y＝－x＋180. ……………4′ ‎ ‎(2)W＝(x－100) y＝(x－100)( －x＋180) ……………5′‎ ‎ ＝－x2＋280x－18000 ……………6′‎ ‎ ＝－(x－140) 2＋1600 ……………7′‎ 当售价定为140元, W最大＝1600.‎ ‎∴售价定为140元/件时,每天最大利润W＝1600元 ……………8′ ‎ ‎19. (1)证明:梯形ABCD中,∵AD∥BC,AB＝DC.‎ ‎∴∠B＝∠C＝60°. ……………1′‎ ‎∵∠APC＝∠B＋∠BAP,‎ 即∠APE＋∠EPC＝∠B＋∠BAP.‎ ‎∵∠APE＝∠B,‎ ‎∴∠BAP＝∠EPC. ……………2′‎ ‎∴△APB∽△PEC. ……………3′‎ ‎(2)过点A作AF∥CD交BC于F.‎ 则四边形ADCF为平行四边形,△ABC为等边三角形. ……………4′‎ ‎∴CF＝AD＝3,AB＝BF＝7－3＝4.‎ ‎∵△APB∽△PEC, ……………5′‎ ‎∴＝,‎ 设BP＝x,则PC＝7－x,又EC＝3, AB＝4,‎ ‎∴＝ ……………6′‎ 整理,得x2－7x＋12＝0.‎ 解得 x1＝3, x2＝4. ……………7′‎ 经检验, x1＝3, x2＝4是所列方程的根,‎ ‎∴BP的长为3或4. ……………8′ ‎ A ‎ B ‎ D ‎ CB ‎ PB ‎ E ‎ F ‎ ‎20.解：（1）根据题意得ｍ≠1 ……………1′‎ ‎ △＝（–2ｍ）2－4（ｍ－1）（ｍ＋1）＝4 ……………2′‎ ‎ ∴x1＝ ＝ ……………3′‎ x2＝ ……………4′‎ ‎（2）由（1）知x1＝= ……………5′‎ ‎∵方程的两个根都是正整数，‎ ‎∴是正整数， ……………6′‎ ‎∴ｍ－1=1或2. ……………7′‎ ‎∴ｍ=2或3 ……………8′‎ ‎21.解:(1)如图,过点M作CD∥AB,NE⊥AB. ……………1′‎ ‎ 在Rt△ACM中，∠CAM=36.5°，AM=5，‎ ‎ ∴sin36.5°＝ ＝0.6，‎ ‎ ∴CM＝3，AC＝4. ……………2′‎ ‎ 在Rt△ANE中, ∠NAE=90°－53.5°=36.5°，AN=10，‎ ‎ ∴sin36.5°＝ ＝0.6‎ ‎∴NE＝6，AE＝8. ……………3′‎ 在Rt△MND中,MD＝5，ND＝2.‎ ‎∴MN＝ ＝ (km) ……………4′‎ ‎ (2)作点N关于AB的对称点G，连接MG交AB于点P.‎ ‎ 点P即为站点. ……………5′‎ ‎ ∴PM＋PN＝PM＋PG＝MG. ……………6′‎ ‎ 在Rt△MDG中,MG＝＝＝(km) ……………7′‎ ‎ ∴最短距离为 km ……………8′‎ P 北A A ‎ N ‎ M ‎ B ‎ C D G E ‎22．解：（1）把点（b－2，2b2－5b－1）代入解析式，得 ‎2b2－5b－1=（b－2）2+b（b－2）－3b+3， ……………1′‎ 解得b=2.‎ ‎∴抛物线的解析式为y=x2+2x－3. ……………2′‎ ‎（2）由x2+2x－3=0，得x=－3或x=1.‎ ‎∴A（－3，0）、B（1，0）、C（0，－3）.‎ 抛物线的对称轴是直线x=－1，圆心M在直线x=－1上. ……………3′‎ ‎∴设M（－1，n），作MG⊥x轴于G，MH⊥y轴于H，连接MC、MB.‎ ‎∴MH=1，BG=2. ……………4′‎ ‎∵MB=MC，∴BG2+MG2=MH2+CH2，‎ 即4+n2=1+（3+n）2，解得n=－1，∴点M（－1，－1） ……………5′‎ ‎（3）如图，由M（－1，－1），得MG=MH.‎ ‎∵MA=MD，∴Rt△AMG≌RtDMH，∴∠1=∠2.‎ 由旋转可知∠3=∠4. ∴△AME≌△DMF.‎ 若△DMF为等腰三角形，则△AME为等腰三角形. ……………6′‎ 设E（x，0），△AME为等腰三角形，分三种情况：‎ ‎①AE=AM=，则x=－3，∴E（－3，0）；‎ ‎②∵M在AB的垂直平分线上，‎ ‎∴MA=ME=MB，∴E（1，0） ……………7′‎ ‎③点E在AM的垂直平分线上，则AE=ME. ‎ AE=x+3，ME2=MG2+EG2=1+（－1－x）2，∴（x+3）2=1+（－1－x）2，解得x=，∴E（，0）.‎ ‎∴所求点E的坐标为（－3，0），（1，0），（，0） ……………8′‎