2013年湖南省益阳市中考数学试题（含答案） 8页

益阳市2013年普通初中毕业学业考试试卷 数 学 注意事项：1. 本学科试卷分试题卷和答题卡两部分；‎ ‎2. 请将姓名、准考证号等相关信息按要求填写在答题卡上；‎ ‎3. 请按答题卡上的注意事项在答题卡上作答，答在试题卷上无效；‎ ‎4. 本学科为闭卷考试，考试时量为90分钟，卷面满分为120分；‎ ‎5. 考试结束后，请将试题卷和答题卡一并交回．‎ 试 题 卷 一、选择题（本大题共8小题，每小题4分，共32分．在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．据益阳市统计局在网上发布的数据，2012年益阳市地区生产总值（GDP ）突破千亿元大关，达到了1020亿元，将102 000 000 000用科学记数法表示正确的是 A． B． C． D．‎ ‎2．下列运算正确的是 A． B． ‎ C． D． ‎ ‎3．分式方程的解是 A．x = B．x = C．x = D．x =‎ ‎4．实施新课改以来，某班学生经常采用“小组合作学习”的方式进行学习，学习委员小兵每周对各小组合作学习的情况进行了综合评分．下表是其中一周的统计数据：‎ 组 别 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ 分 值 ‎90‎ ‎95[来源:学科网ZXXK]‎ ‎90‎ ‎88‎ ‎90‎ ‎92‎ ‎85‎ 这组数据的中位数和众数分别是 A．88，90 B．90，90 C．88，95 D．90，95 ‎ 主视图 左视图 俯视图 图1‎ ‎1‎ ‎2‎ A B C D 图2‎ ‎5．一个物体由多个完全相同的小正方体组成，它的三视图如图1所示，那么组成这个物体的小正方体的个数为 A. 2个 ‎ B. 3个　　　 ‎ C. 5个 [来源:学科网ZXXK]‎ D. 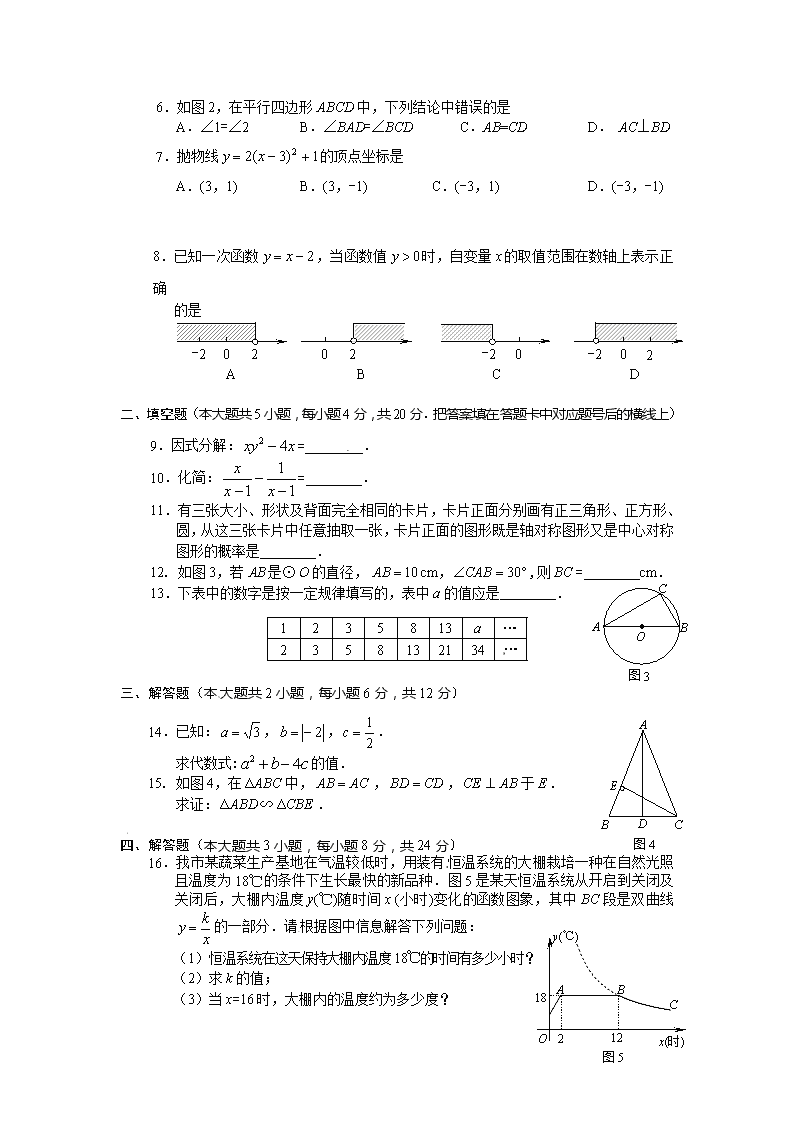10个 ‎6．如图2，在平行四边形ABCD中，下列结论中错误的是 ‎ A．∠1=∠2 B．∠BAD=∠BCD C．AB=CD D． AC⊥BD ‎7．抛物线的顶点坐标是 A．(3，1) B．(3，-1) C．(-3，1) D．(-3，-1) ‎ ‎8．已知一次函数，当函数值时，自变量的取值范围在数轴上表示正确 的是 ‎0‎ ‎2‎ ‎-2‎ ‎0‎ ‎0‎ ‎2‎ ‎-2‎ ‎-2‎ ‎0‎ ‎2‎ ‎ ‎ A B C D 二、填空题（本大题共5小题，每小题4分，共20分．把答案填在答题卡中对应题号后的横线上）‎ ‎9．因式分解：= ． ‎ ‎10．化简：= ． ‎ O A B 图3‎ C ‎11．有三张大小、形状及背面完全相同的卡片，卡片正面分别画有正三角形、正方形、圆，从这三张卡片中任意抽取一张，卡片正面的图形既是轴对称图形又是中心对称图形的概率是 ．‎ ‎12. 如图3，若是⊙的直径，cm，,则= cm．‎ ‎13．下表中的数字是按一定规律填写的，表中a的值应是 ．‎ ‎1‎ ‎2‎ ‎3‎ ‎5‎ ‎8‎ ‎13‎ a ‎…‎ ‎2‎ ‎3‎ ‎5‎ ‎8‎ ‎13‎ ‎21‎ ‎34‎ ‎…‎ 三、解答题（本大题共2小题，每小题6分，共12分）‎ A B D C E 图4‎ ‎14．已知：，，．‎ ‎　　求代数式:的值．‎ ‎15. 如图4，在中，，，于. ‎ 求证：．‎ ‎ ‎ 四、解答题（本大题共3小题，每小题8分，共24分）‎ x(时)‎ y(℃)‎ ‎18‎ ‎2‎ ‎12‎ O 图5‎ A B C ‎16．我市某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种．图5是某天恒温系统从开启到关闭及关闭后，大棚内温度y(℃)随时间x (小时)变化的函数图象，其中BC段是双曲线的一部分．请根据图中信息解答下列问题：‎ ‎（1）恒温系统在这天保持大棚内温度18℃的时间有多少小时？‎ ‎（2）求k的值；‎ ‎（3）当x=16时，大棚内的温度约为多少度？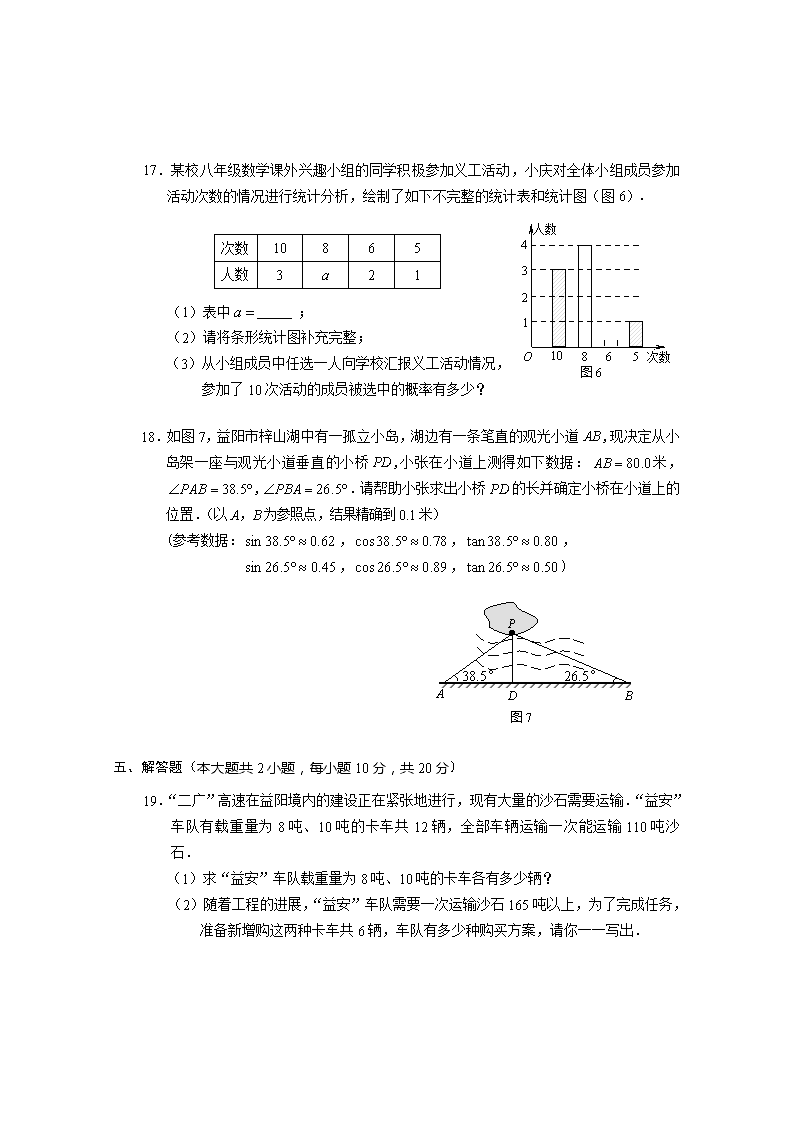‎ ‎1‎ ‎2‎ ‎3‎ 次数 人数 ‎10‎ ‎8‎ ‎6‎ ‎5‎ ‎4‎ 图6‎ O ‎17．某校八年级数学课外兴趣小组的同学积极参加义工活动，小庆对全体小组成员参加活动次数的情况进行统计分析，绘制了如下不完整的统计表和统计图（图6）.‎ 次数 ‎10‎ ‎8‎ ‎6‎ ‎5‎ 人数 ‎3‎ a ‎2‎ ‎1‎ ‎（1）表中 ；‎ ‎（2）请将条形统计图补充完整；‎ ‎（3）从小组成员中任选一人向学校汇报义工活动情况，‎ 参加了10次活动的成员被选中的概率有多少？‎ ‎18．如图7，益阳市梓山湖中有一孤立小岛，湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥,小张在小道上测得如下数据：米，,．请帮助小张求出小桥PD的长并确定小桥在小道上的位置．（以A，B为参照点，结果精确到0.1米）‎ ‎(参考数据：，，，‎ ‎，，) ‎ B D ‎38.5°‎ ‎26.5°‎ A 图7‎ P 五、解答题（本大题共2小题，每小题10分，共20分）‎ ‎19．“二广”高速在益阳境内的建设正在紧张地进行，现有大量的沙石需要运输．“益安”车队有载重量为8吨、10吨的卡车共12辆，全部车辆运输一次能运输110吨沙石．‎ ‎（1）求“益安”车队载重量为8吨、10吨的卡车各有多少辆？‎ ‎（2）随着工程的进展，“益安”车队需要一次运输沙石165吨以上，为了完成任务，准备新增购这两种卡车共6辆，车队有多少种购买方案，请你一一写出．‎ ‎[来源:Zxxk.Com]‎ ‎20．如图8，在中，，，的平分线交于．‎ ‎ （1）求证：；‎ ‎（2）如图8（2），过点作∥交于,将绕点逆时针旋转角得到，连结,，求证：；‎ ‎ （3）在（2）的旋转过程中是否存在∥？若存在，求出相应的旋转角；‎ B C 图8（1）‎ A E ‎36°‎ E B C F 图8（备用图）‎ A ‎36°‎ 图8（2）‎ E B C F ‎36°‎ A 若不存在，请说明理由．‎ 图8‎ 六、解答题（本题满分12分）‎ ‎21．阅读材料：如图9，在平面直角坐标系中，、两点的坐标分别为，‎ ‎ ，中点的坐标为．由，得，‎ A P B O 图9‎ 同理，所以的中点坐标为．‎ 由勾股定理得，所以、两点 间的距离公式为．‎ 注：上述公式对、在平面直角坐标系中其它位置也成立．‎ ‎ ‎ 解答下列问题：‎ 图10‎ y x A B P C O ‎1‎ ‎1‎ 如图10，直线：与抛物线交于、两点，为的中点，‎ 过作轴的垂线交抛物线于点．‎ ‎（1）求、两点的坐标及点的坐标；‎ ‎（2）连结，求证为直角三角形；[来源:学|科|网Z|X|X|K]‎ ‎（3）将直线平移到点时得到直线，求两 直线与的距离．‎ 益阳市2013年普通初中毕业学业考试 数学参考答案及评分标准 一、选择题（本大题共8小题，每小题4分，共32分）.‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 A C B B C D A B 二、填空题（本大题共5小题，每小题4分，共20分）.‎ ‎9．；10．1；11．；12．5；13．21．‎ 三、解答题（本大题共2小题，每小题6分，共12分）．‎ ‎14.解：当，，时，‎ ‎= ‎ ‎　　　 = 5分 ‎　　　　　　　 = 6分 ‎ 15.证明：在中，，，‎ ‎∴， 2分 ‎∵，‎ ‎∴， 4分 又，‎ ‎∴． 6分 四、解答题（本大题共3小题，每小题8分，共24分） ‎ ‎16. 解：（1）恒温系统在这天保持大棚温度18℃的时间为10小时． 2分 ‎ （2）∵点(12，18)在双曲线上，‎ ‎1‎ ‎2‎ ‎3‎ 次数 人数 ‎10‎ ‎8‎ ‎6‎ ‎5‎ ‎4‎ 第17题解图 O ‎ ∴，‎ ‎∴. 5分 ‎（3）当x=16时，，　　‎ 所以当x=16时，大棚内的温度约为13.5℃． 8分 ‎17. 解:（1）4． 　 2分 ‎（2）如图． 5分 ‎（3）∵小组成员共10人，参加了10次活动的 成员有3人，∴，‎ 答：从小组成员中任选一人向学校汇报义工活动 情况，参加了10次活动的成员被选中的概率是． 8分 ‎18．解：设米，‎ ‎∵，‎ ‎∴．‎ ‎ 在Rt△PAD中，，‎ ‎ ∴． 3分 在Rt△PBD中，，‎ ‎ ∴． 5分 又AB=80.0，‎ ‎∴．‎ ‎∴，即．‎ ‎∴． [来源:学_科_网Z_X_X_K]‎ 答：小桥PD的长度约为24.6米，位于AB之间距B点约49.2米． ８分 五、解答题（本大题共2小题，每小题10分，共20分） ‎ ‎19．解：（1）设“益安”车队载重量为8吨、10吨的卡车分别有x辆、y辆，‎ 根据题意得：， 2分 解之得． ‎ ‎∴“益安”车队载重量为8吨的卡车有5辆，10吨的卡车有7辆； 5分 ‎（2）设载重量为8吨的卡车增加了z辆，‎ 依题意得：， 7分 解之得：‎ ‎∵且为整数，‎ ‎∴0,1,2 ； ‎ ‎∴6,5,4． 8分 ‎∴车队共有3种购车方案：‎ ‎①载重量为8吨的卡车不购买，10吨的卡车购买6辆；‎ ‎②载重量为8吨的卡车购买1辆，10吨的卡车购买5辆；‎ ‎③载重量为8吨的卡车购买2辆，10吨的卡车购买4辆． 10分 ‎20．解：（1）证明：∵，，‎ ‎∴, 1分 ‎ 又平分，‎ ‎∴，‎ ‎∴‎ ‎∴，，‎ ‎∴，， ‎ ‎∴. 3分 ‎（2）∵且∥，∴；‎ 由旋转的性质可知：，，‎ ‎∴≌，‎ ‎∴. 6分 ‎（3）存在∥，‎ 由（1）可知，所以，在绕点逆时针旋转过程中，点经过的路径(圆弧)与过点且与平行的直线交于M、N两点，如图．‎ ‎①当点的像与点重合时，则四边形为等腰梯形，‎ ‎36°‎ B C A E F 第20题解图 ‎ ∴，又，‎ ‎∴． 8分 ‎②当点的像与点重合时，‎ 由得，，‎ ‎∵，‎ ‎∴，‎ ‎ ∴，‎ ‎∴．‎ 所以，当旋转角为或时，∥． 10分 六、解答题（本题满分12分） ‎ ‎21．解：（1）由，解得， ．‎ 则,两点的坐标分别为：，， 2分 ‎∵是,的中点，由中点坐标公式得点坐标为，‎ 又轴交抛物线于点，将代入中得,‎ ‎∴点坐标为． 4分 ‎（2）由两点间距离公式得：‎ ‎，，‎ ‎∴， 6分 ‎∴，，‎ ‎∴，即 图10‎ y x A B P C O ‎1‎ ‎1‎ H G ‎ ∴ 为直角三角形． 8分 ‎（3）过点作于 ，过点作于 ，‎ 则点的坐标为， ９分 ‎∴ ,‎ ‎∴．‎ 又直线与之间的距离等于点C到的距离CG，‎ ‎∴直线与之间的距离为． 12分