中考数学试题精选50题：二次函数及其应用 30页

‎2020年全国中考数学试题精选50题：二次函数及其应用 一、单选题 ‎ ‎1.（2020·玉林）把二次函数y＝ax2+bx+c（a＞0）的图象作关于x轴的对称变换，所得图象的解析式为y＝﹣a（x﹣1）2+4a，若（m﹣1）a+b+c≤0，则m的最大值是（   ） ‎ A. ﹣4                                          B. 0                                          C. 2                                          D. 6‎ ‎2.（2020·铁岭）如图，二次函数 的图象的对称轴是直线 ，则以下四个结论中：① ，② ，③ ，④ .正确的个数是（   ） ‎ A. 1                                           B. 2                                           C. 3                                           D. 4‎ ‎3.（2020·盘锦）如图，四边形 是边长为1的正方形，点 是射线 上的动点（点 不与点 ，点 重合），点 在线段 的延长线上，且 ，连接 ，将 绕点 顺时针旋转90°得到 ，连接 .设 ，四边形 的面积为 ，下列图象能正确反映出 与 的函数关系的是（   ） ‎ A.                                   B.  C.                               D. ‎ ‎4.（2020·阜新）已知二次函数 ，则下列关于这个函数图象和性质的说法，正确的是（   ） ‎ A. 图象的开口向上                                                  B. 图象的顶点坐标是 C. 当 时，y随x的增大而增大                          D. 图象与x轴有唯一交点 ‎5.（2020·丹东）如图，二次函数 （ ）的图象与 轴交于 ， 两点，与 轴交于点 ，点 坐标为 ，点 在 与 之间（不包括这两点），抛物线的顶点为 ，对称轴为直线 ，有以下结论：① ；②若点 ，点 是函数图象上的两点，则 ；③ ；④ 可以是等腰直角三形.其中正确的有（   ） ‎ A. 1个                                       B. 2个                                       C. 3个                                       D. 4个 ‎6.（2020·镇江）点P(m，n)在以y轴为对称轴的二次函数y＝x2+ax+4的图象上.则m﹣n的最大值等于（   ） ‎ A.                                     B. 4                                    C. ﹣                                     D. ﹣ ‎ ‎7.（2020·绵阳）三孔桥横截面的三个孔都呈抛物线形，两小孔形状、大小完全相同．当水面刚好淹没小孔时，大孔水面宽度为10米，孔顶离水面1.5米；当水位下降，大孔水面宽度为14米时，单个小孔的水面宽度为4米，若大孔水面宽度为20米，则单个小孔的水面宽度为（   ） ‎ A. 4 米                               B. 5 米                               C. 2 米                               D. 7米 ‎8.（2020·眉山）已知二次函数 （ 为常数）的图象与x轴有交点，且当 时，y随x的增大而增大，则a的取值范围是（   ） ‎ A.                            B.                            C.                            D. ‎ ‎9.（2020·凉山州）二次函数 的图象如图所示，有如下结论：① ；② ；③ ；④ （m为实数）．其中符合题意结论的个数是（    ） ‎ A. 1个                                       B. 2个                                       C. 3个                                       D. 4个 ‎10.（2020·威海）如图，抛物线 交x轴于点A，B，交 轴于点C．若点A坐标为 ，对称轴为直线 ，则下列结论错误的是（    ） ‎ A. 二次函数的最大值为             B.             C.             D. ‎ ‎11.（2020·东营）如图，已知抛物线 的图象与x轴交于 两点，其对称轴与x轴交于点C其中 两点的横坐标分别为-1和1下列说法错误的是（  ） ‎ A.             B.             C.             D. 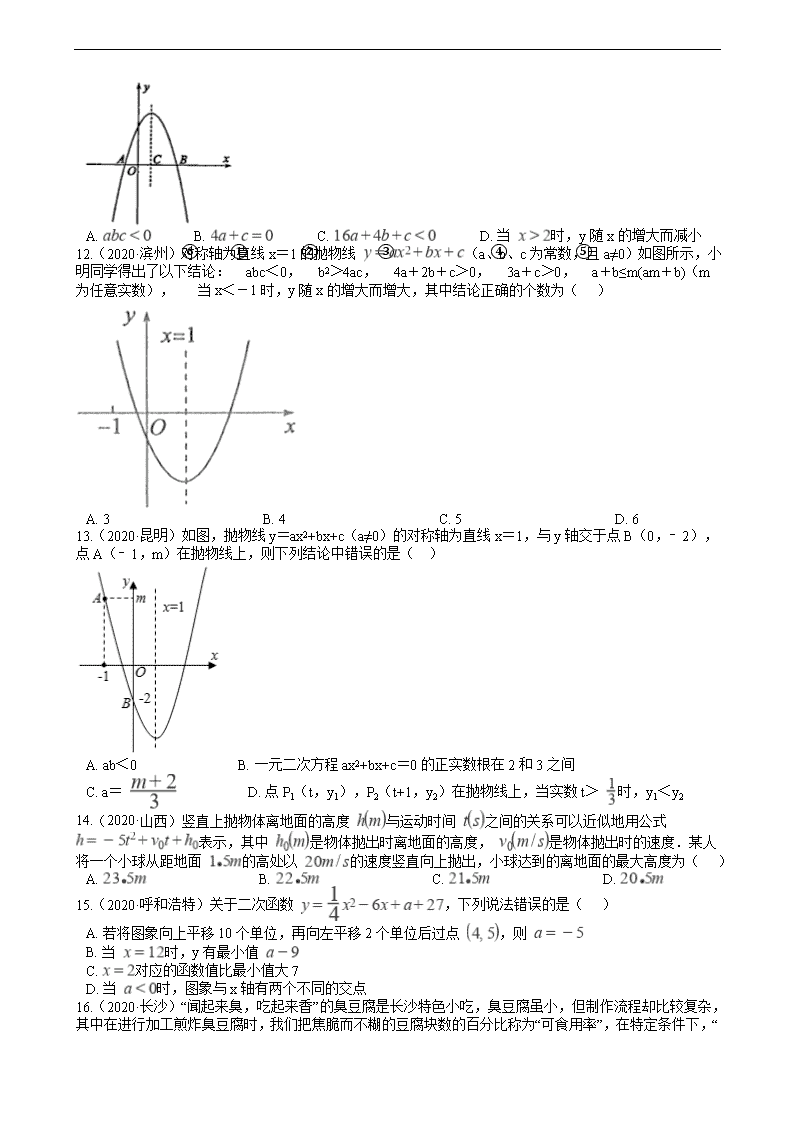当 时，y随x的增大而减小 ‎12.（2020·滨州）对称轴为直线x＝1的抛物线 （a、b、c为常数，且a≠0）如图所示，小明同学得出了以下结论：①abc＜0，②b2＞4ac，③4a＋2b＋c＞0，④3a＋c＞0，⑤a＋b≤m(am＋b)（m为任意实数）， ⑥当x＜－1时，y随x的增大而增大，其中结论正确的个数为（    ） ‎ A. 3                                           B. 4                                           C. 5                                           D. 6‎ ‎13.（2020·昆明）如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与y轴交于点B（0，﹣2），点A（﹣1，m）在抛物线上，则下列结论中错误的是（   ） ‎ A. ab＜0                             B. 一元二次方程ax2+bx+c＝0的正实数根在2和3之间 C. a＝                    D. 点P1（t，y1），P2（t+1，y2）在抛物线上，当实数t＞ 时，y1＜y2‎ ‎14.（2020·山西）竖直上抛物体离地面的高度 与运动时间 之间的关系可以近似地用公式 表示，其中 是物体抛出时离地面的高度， 是物体抛出时的速度．某人将一个小球从距地面 的高处以 的速度竖直向上抛出，小球达到的离地面的最大高度为（    ） ‎ A.                                 B.                                 C.                                 D. ‎ ‎15.（2020·呼和浩特）关于二次函数 ，下列说法错误的是（    ） ‎ A. 若将图象向上平移10个单位，再向左平移2个单位后过点 ，则 B. 当 时，y有最小值 C. 对应的函数值比最小值大7 D. 当 时，图象与x轴有两个不同的交点 ‎16.（2020·长沙）“闻起来臭，吃起来香”的臭豆腐是长沙特色小吃，臭豆腐虽小，但制作流程却比较复杂，其中在进行加工煎炸臭豆腐时，我们把焦脆而不糊的豆腐块数的百分比称为“可食用率”，在特定条件下，“‎ 可食用率”p与加工煎炸的时间t（单位：分钟）近似满足函数关系式： （ a，b，c为常数），如图纪录了三次实验数据，根据上述函数关系和实验数据，可以得到加工煎炸臭豆腐的最佳时间为(    ) ‎ A. 3.50分钟                            B. 4.05分钟                            C. 3.75分钟                            D. 4.25分钟 ‎17.（2020·深圳）二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法错误的是（    ） ‎ A.                    B. 4ac-b2<0                   C. 3a+c=0                   D. ax2+bx+c=n+1无实数根 ‎18.（2020·广东）把函数 的图象向右平移1个单位长度，平移后图象的函数解析式为（    ） ‎ A.                  B.                  C.                  D. ‎ ‎19.（2020·广东）如图，抛物线 的对称轴是 ．下列结论：① ；② ；③ ；④ ，正确的有（    ） ‎ A. 4个                                       B. 3个                                       C. 2个                                       D. 1个 ‎20.（2020·襄阳）二次函数 的图象如图所示，下列结论：① ；② ；③ ；④当 时，y随x的增大而减小，其中正确的有（   ） ‎ A. 4个                                       B. 3个                                       C. 2个                                       D. 1个 ‎21.（2020·鄂州）如图，抛物线 与 轴交于点 和B，与y轴交于点 .下列结论：① ；② ；③ ；④ ，其中正确的结论个数为（   ） ‎ A. 4                                        B. 2个                                        C. 3个                                        D. 4个 ‎22.（2020·安顺）已知二次函数 的图象经过 与 两点，关于x的方程 有两个根，其中一个根是3.则关于x的方程 有两个整数根，这两个整数根是（   ） ‎ A. -2或0                                  B. -4或2                                  C. -5或3                                  D. -6或4‎ ‎23.（2020·遂宁）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，对称轴为直线x＝﹣1，下列结论错误的是（    ） ‎ A. b2＞4ac                B. abc＞0                C. a﹣c＜0                D. am2+bm≥a﹣b（m为任意实数）‎ ‎24.（2020·泸县）已知二次函数 （其中x是自变量）的图象经过不同两点 ， ，且该二次函数的图象与x轴有公共点，则 的值（    ） ‎ A. -1                                           B. 2                                           C. 3                                           D. 4‎ ‎25.（2020·甘孜）如图，二次函数 的图象与 轴交于 ，B两点，下列说法错误的是（    ） ‎ A.                                                                   B. 图象的对称轴为直线 C. 点B的坐标为                                               D. 当 时，y随x的增大而增大 ‎26.（2020·枣庄）如图，已知抛物线 的对称轴为直线 ．给出下列结论： ‎ ‎① ；      ② ；       ③ ；      ④ ．‎ 其中，正确的结论有（    ）‎ A. 1个                                       B. 2个                                       C. 3个                                       D. 4个 ‎27.（2020·泰安）在同一平面直角坐标系内，二次函数 与一次函数 的图象可能是（   ） ‎ A.                B.                C.                D. ‎ ‎28.（2020·青岛）已知在同一直角坐标系中二次函数 和反比例函数 的图象如图所示，则一次函数 的图象可能是（    ） ‎ A.            B.            C.            D. ‎ ‎29.（2020·株洲）二次函数 ，若 ， ，点 ， 在该二次函数的图象上，其中 ， ，则（    ） ‎ A.                      B.                      C.                      D. 、 的大小无法确定 ‎30.（2020·湘西州）已知二次函数 图象的对称轴为 ，其图象如图所示，现有下列结论：① ；② ；③ ；④ ；⑤ ．正确的是（    ） ‎ A. ①③                                     B. ②⑤                                     C. ③④                                     D. ④⑤‎ 二、填空题 ‎ ‎31.（2020·朝阳）抛物线 与x轴有交点，则k的取值范围是________. ‎ ‎32.（2020·雅安）从 中任取一数作为 ，使抛物线 的开口向上的概率为________． ‎ ‎33.（2020·烟台）二次函数y＝ax2+bx+c的图象如图所示，下列结论：①ab＞0；②a+b﹣1＝0；③a＞1；④关于x的一元二次方程ax2+bx+c＝0的一个根为1，另一个根为﹣ ．其中正确结论的序号是________． ‎ ‎34.（2020·威海）下表中y与x的数据满足我们初中学过的某种函数关系，其函数表达式为________． ‎ ‎……‎ ‎-1‎ ‎0‎ ‎1‎ ‎3‎ ‎……‎ ‎……‎ ‎0‎ ‎3‎ ‎4‎ ‎0‎ ‎……‎ ‎35.（2020·上海）如果将抛物线y=x2向上平移3个单位，那么所得新抛物线的表达式是________． ‎ ‎36.（2020·包头）在平面直角坐标系中，已知 和 是抛物线 上的两点，将抛物线 的图象向上平移n（n是正整数）个单位，使平移后的图象与x轴没有交点，则n的最小值为________． ‎ ‎37.（2020·黑龙江）将抛物线y=(x－1)2－5关于y轴对称，再向右平移3个单位长度后顶点的坐标是________． ‎ ‎38.（2020·荆州）我们约定： 为函数 的关联数，当其图象与坐标轴交点的横、纵坐标均为整数时，该交点为“整交点”，若关联数为 的函数图象与x轴有两个整交点（m为正整数），则这个函数图象上整交点的坐标为________. ‎ ‎39.（2020·无锡）二次函数 的图像过点 ，且与y轴交于点B，点M在该抛物线的对称轴上，若 是以 为直角边的直角三角形，则点M的坐标为________. ‎ ‎40.（2020·南京）下列关于二次函数 （ 为常数）的结论，①该函数的图象与函数 的图象形状相同；②该函数的图象一定经过点 ；③当 时，y随x的增大而减小；④该函数的图象的顶点在函数 的图像上，其中所有正确的结论序号是________. ‎ 三、综合题 ‎ ‎41.（2020·盘锦）某服装厂生产 品种服装，每件成本为71元，零售商到此服装厂一次性批发 品牌服装 件时，批发单价为 元， 与 之间满足如图所示的函数关系，其中批发件数 为10的正整数倍. ‎ ‎（1）当 时， 与 的函数关系式为________. ‎ ‎（2）某零售商到此服装厂一次性批发 品牌服装200件，需要支付多少元？ ‎ ‎（3）零售商到此服装厂一次性批发 品牌服装 件，服装厂的利润为 元，问： 为何值时， 最大？最大值是多少？ ‎ ‎42.（2020·锦州）某水果超市以每千克20元的价格购进一批樱桃，规定每千克樱桃售价不低于进价又不高于40元，经市场调查发现，樱桃的日销售量y（千克）与每千克售价x（元）满足一次函数关系，其部分对应数据如下表所示： ‎ 每千克售价x（元）‎ ‎…‎ ‎25‎ ‎30‎ ‎35‎ ‎…‎ 日销售量y（千克）‎ ‎…‎ ‎110‎ ‎100‎ ‎90‎ ‎…‎ ‎（1）求y与x之间的函数关系式； ‎ ‎（2）该超市要想获得1000的日销售利润，每千克樱桃的售价应定为多少元？ ‎ ‎（3）当每千克樱桃的售价定为多少元时，日销售利润最大？最大利润是多少？ ‎ ‎43.（2020·朝阳）某公司销售一种商品，成本为每件30元，经过市场调查发现，该商品的日销售量y（件）与销售单价x（元）是一次函数关系，其销售单价、日销售量的三组对应数值如下表： ‎ 销售单价x（元）‎ ‎40‎ ‎60‎ ‎80‎ 日销售量y（件）‎ ‎80‎ ‎60‎ ‎40‎ ‎（1）直接写出y与x的关系式________； ‎ ‎（2）求公司销售该商品获得的最大日利润； ‎ ‎（3）销售一段时间以后，由于某种原因，该商品每件成本增加了10元，若物价部门规定该商品销售单价不能超过a元，在日销售量y（件）与销售单价x（元）保持（1）中函数关系不变的情况下，该商品的日销售最大利润是1500元，求a的值. ‎ ‎44.（2020·泰州）如图，在 中， ， ， ， 为 边上的动点（与 、 不重合）， ，交 于点 ，连接 ，设 ， 的面积为 . ‎ ‎（1）用含 的代数式表示 的长； ‎ ‎（2）求 与 的函数表达式，并求当 随 增大而减小时 的取值范围. ‎ ‎45.（2020·雅安）如图，已知边长为10的正方形 是 边上一动点（与 不重合），连结 是 延长线上的点，过点E作 的垂线交 的角平分线于点F，若 ． ‎ ‎（1）求证： ； ‎ ‎（2）若 ，求 的面积； ‎ ‎（3）请直接写出 为何值时， 的面积最大． ‎ ‎46.（2020·威海）已知，在平面直角坐标系中，抛物线 的顶点为A，点B的坐标为 ‎ ‎（1）求抛物线过点B时顶点A的坐标 ‎ ‎（2）点A的坐标记为 ，求y与x的函数表达式； ‎ ‎（3）已知C点的坐标为 ，当m取何值时，抛物线 与线段 只有一个交点 ‎ ‎47.（2020·呼伦贝尔）某商店销售一种销售成本为每件40元的玩具，若按每件50元销售，一个月可售出500件，销售价每涨1元，月销量就减少10件．设销售价为每件x元 ，月销量为y件，月销售利润为w元． ‎ ‎（1）写出y与x的函数解析式和w与x的函数解析式； ‎ ‎（2）商店要在月销售成本不超过10000的情况下，使月销售利润达到8000元，销售价应定为每件多少元； ‎ ‎（3）当销售价定为每件多少元时会获得最大利润？求出最大利润． ‎ ‎48.（2020·昆明）如图，两条抛物线 ， 相交于A，B两点，点A在x轴负半轴上，且为抛物线 的最高点. ‎ ‎（1）求抛物线 的解析式和点B的坐标； ‎ ‎（2）点C是抛物线 上A，B之间的一点，过点C作x轴的垂线交 于点D，当线段CD取最大值时，求 . ‎ ‎49.（2020·营口）某超市销售一款“免洗洗手液”，这款“免洗洗手液”的成本价为每瓶16元，当销售单价定为20元时，每天可售出80瓶.根据市场行情，现决定降价销售.市场调查反映：销售单价每降低0.5元，则每天可多售出20瓶（销售单价不低于成本价），若设这款“免洗洗手液”的销售单价为x（元），每天的销售量为y（瓶）. ‎ ‎（1）求每天的销售量y（瓶）与销售单价x（元）之间的函数关系式； ‎ ‎（2）当销售单价为多少元时，销售这款“免洗洗手液”每天的销售利润最大，最大利润为多少元？ ‎ ‎50.（2020·宿迁）某超市经销一种商品，每千克成本为50元，经试销发现，该种商品的每天销售量y（千克）与销售单价x（元/千克）满足一次函数关系，其每天销售单价，销售量的四组对应值如下表所示： ‎ 销售单价x（元/千克）‎ ‎55‎ ‎60‎ ‎65‎ ‎70‎ 销售量y（千克）‎ ‎70‎ ‎60‎ ‎50‎ ‎40‎ ‎（1）求y（千克）与x（元/千克）之间的函数表达式； ‎ ‎（2）为保证某天获得600元的销售利润，则该天的销售单价应定为多少？ ‎ ‎（3）当销售单价定为多少时，才能使当天的销售利润最大？最大利润是多少？ ‎ 答案解析部分 一、单选题 ‎1.【答案】 D ‎ ‎【解析】【解答】解：∵把二次函数y＝ax2+bx+c（a＞0）的图象作关于x轴的对称变换，所得图象的解析式为y＝﹣a（x﹣1）2+4a， ‎ ‎∴原二次函数的顶点为（1，﹣4a），‎ ‎∴原二次函数为y＝a（x﹣1）2﹣4a＝ax2﹣2ax﹣3a，‎ ‎∴b＝﹣2a，c＝﹣3a，‎ ‎∵（m﹣1）a+b+c≤0，‎ ‎∴（m﹣1）a﹣2a﹣3a≤0，‎ ‎∵a＞0，‎ ‎∴m﹣1﹣2﹣3≤0，即m≤6，‎ ‎∴m的最大值为6，‎ 故答案为：D.‎ ‎【分析】根据关于x对称的点的坐标特征得出原二次函数的顶点为（1，﹣4a），即可得出原二次函数为y＝a（x﹣1）2﹣4a＝ax2﹣2ax﹣3a，和y＝ax2+bx+c比较即可得出b＝﹣2a，c＝﹣3a，代入（m﹣1）a+b+c≤0，即可得到m≤6.‎ ‎2.【答案】 B ‎ ‎【解析】【解答】解：由函数图像的开口向下得 ＜ ‎ 由对称轴为 ＞ 所以 ＞ ‎ 由函数与 轴交于正半轴，所以 ＞ ‎ ‎＜ 故①错误；‎ ‎，‎ ‎ ‎ ‎ 故②正确；‎ ‎ 由交点位置可得： ＞ ，‎ ‎＜ ‎ ‎＞ ，‎ ‎＜ ‎ ‎ ‎ ‎＜ 故③错误；‎ 由图像知：当 ‎ 此时点 在第三象限，‎ ‎＜ ‎ ‎ ‎ ‎＜ 故④正确；‎ 综上：正确的有：②④，‎ 故答案为：B.‎ ‎【分析】由开口方向，对称轴方程，与 轴的交点坐标判断 的符号，从而可判断①②，利用与 轴的交点位置得到 ＞ ，结合 ＜ 可判断③，利用当 结合图像与对称轴可判断④.‎ ‎3.【答案】 B ‎ ‎【解析】【解答】连接DC，如图所示， ‎ 由题可得DE=GE，AE=AF，∠DAE=∠BAF=90°,‎ ‎∴△DAE≌△BAF，‎ ‎∴DE=BF,∠EDA=∠FBA,又∵DE=EG,‎ ‎∴GE=BF,‎ ‎∵∠GEB+∠DEA=∠EDA+∠DEA =90°,‎ ‎∴∠GEB=∠EDA，‎ ‎∴∠GEB=∠FBA，‎ ‎∴GE//BF,且GE=BF，‎ ‎∴四边形GEFB是平行四边形，‎ ‎∵ ，‎ 当 ‎ ‎∴ ， ，‎ ‎，‎ ‎∴ ，‎ 当x＞1时，‎ ‎∴ ， ，‎ ‎，‎ ‎∴ ，‎ 故答案为：B.‎ ‎【分析】连接DC，根据已知条件证明所求得四边形是平行四边形，从而可得 ，再分类讨论即可得到结果；‎ ‎4.【答案】 C ‎ ‎【解析】【解答】解： ＜ 所以抛物线的开口向下，故A错误， ‎ 所以抛物线的顶点为： 故B错误，‎ 当 ，即在抛物线的对称轴的左侧，y随x的增大而增大，故C正确，‎ ‎ ‎ ‎＞ ‎ 所以抛物线与 轴有两个交点，故D错误，‎ 故答案为：C.‎ ‎【分析】由抛物线的二次项的系数判断A，把抛物线写成顶点式，可判断B，由 得抛物线的图像在对称轴的左侧，从而得到y随x的增大而增大，利用 的值，判断D.‎ ‎5.【答案】 B ‎ ‎【解析】【解答】解：①由开口可知：a＜0， ‎ ‎∴对称轴x=−    ＞0， ‎ ‎∴b＞0，‎ 由抛物线与y轴的交点可知：c＞0，‎ ‎∴abc＜0，故①错误；‎ ‎②由于 ＜2＜ ，且（ ，y1）关于直线x=2的对称点的坐标为（ ，y1），‎ ‎∵ ＜ ，‎ ‎∴y1＜y2 ， 故②正确，‎ ‎③∵− =2，‎ ‎∴b=-4a，‎ ‎∵x=-1，y=0，‎ ‎∴a-b+c=0，‎ ‎∴c=-5a，‎ ‎∵2＜c＜3，‎ ‎∴2＜-5a＜3，‎ ‎∴ ，故③正确 ‎④根据抛物线的对称性可知，AB=6，‎ ‎∴ ，‎ 假定抛物线经过（0，2），（-1，0），（5，0），‎ 设抛物线的解析式为y=a(x+1)(x-5)，则a=- ，‎ ‎ ∴y=- (x-2)2+ ‎ ‎∵ ＞3‎ ‎∴ 不可以是等腰直角三形.故④错误.  ‎ 所以正确的是②③，共2个.‎ 故答案为：B.‎ ‎【分析】观察抛物线的开口方向，可确定出a的取值范围，抛物线与y轴的交点位置，可以确定出c的取值范围，根据对称轴的位置：左同右异，结合a的值，可确定出b的取值范围，由此可得到abc的符号，可对①作出判断；利用二次函数的增减性，可得到y1和y2的大小关系，可对②作出判断；利用二次函数的对称轴为直线x=2，可得到b=-4a，再根据当x=-1时y=0，可推出c=-5a，然后由函数图像可知2＜c＜3，由此可得到a的取值范围，可对③作出判断；利用二次函数的对称性，可以设抛物线的解析式为y=a(x+1)(x-5)，由a的值及等腰直角三角形的性质，可对④作出判断；综上所述可得到正确结论的个数。‎ ‎6.【答案】 C ‎ ‎【解析】【解答】解：∵点P（m，n）在以y轴为对称轴的二次函数y＝x2+ax+4的图象上， ‎ ‎∴a＝0，‎ ‎∴n＝m2+4，‎ ‎∴m﹣n＝m﹣（m2+4）＝﹣m2+m﹣4＝﹣（m﹣ ）2﹣ ，‎ ‎∴当m＝ 时，m﹣n取得最大值，此时m﹣n＝﹣ ，‎ 故答案为：C.‎ ‎【分析】根据题意，可以得到a的值以及m和n的关系，然后将m、n作差，利用二次函数的性质，即可求出m﹣n的最大值.‎ ‎7.【答案】 B ‎ ‎【解析】【解答】解：如图，建立如图所示的平面直角坐标系，由题意可得MN=4，EF=14，BC=10，DO= ， ‎ 设大孔所在抛物线解析式为y=ax2+ ，‎ ‎∵BC=10，‎ ‎∴点B（﹣5，0），‎ ‎∴0=a×（﹣5）2+ ，‎ ‎∴a=- ，‎ ‎∴大孔所在抛物线解析式为y=- x2+ ，设点A（b，0），则设顶点为A的小孔所在抛物线的解析式为y=m（x﹣b）2 ， ‎ ‎∵EF=14，‎ ‎∴点E的横坐标为-7，‎ ‎∴点E坐标为（-7，- ），   ‎ ‎∴- =m（x﹣b）2 ， ‎ ‎∴x1= +b，x2=- +b，‎ ‎∴MN=4，‎ ‎∴| +b-（- +b）|=4‎ ‎∴m=- ，‎ ‎∴顶点为A的小孔所在抛物线的解析式为y=- （x﹣b）2 ， ‎ ‎∵大孔水面宽度为20米，‎ ‎∴当x=-10时，y=- ，‎ ‎∴- =- （x﹣b）2 ， ‎ ‎∴x1= +b，x2=- +b，‎ ‎∴单个小孔的水面宽度=|（ +b）-（- +b）|=5 （米），‎ 故答案为：B．‎ ‎【分析】根据题意，可以画出相应的抛物线，然后即可得到大孔所在抛物线解析式，再求出顶点为A的小孔所在抛物线的解析式，将x=﹣10代入可求解．‎ ‎8.【答案】 D ‎ ‎【解析】【解答】解： ‎ ‎∵图象与x轴有交点，‎ ‎∴△=（-2a）2-4（a2-2a-4）≥0‎ 解得a≥-2；‎ ‎∵抛物线的对称轴为直线 ‎ 抛物线开口向上，且当 时，y随x的增大而增大，‎ ‎∴a≤3，‎ ‎∴实数a的取值范围是-2≤a≤3．‎ 故答案为：D．‎ ‎【分析】根据图象与x轴有交点，得出判别式△≥0，从而解得a≥-2，然后求出抛物线的对称轴，结合抛物线开口向上，且当 时，y随x的增大而增大，可得a≤3，从而得出选项．‎ ‎9.【答案】 D ‎ ‎【解析】【解答】解：∵抛物线的开口向上，∴a＞0， ‎ ‎∵抛物线的对称轴是直线x=1，∴ ，‎ ‎∴b＜0， ，故②符合题意；‎ ‎∵抛物线与y轴交于负半轴，∴c＜0，‎ ‎∴ ，故①符合题意；‎ ‎∵当x=3时，y＞0，∴9a+3b+c＞0，‎ ‎∵ ，∴ ，‎ 整理即得： ，故③符合题意；‎ ‎∵当x=1时，二次函数y取最小值a+b+c，‎ ‎∴ （m为实数），即 （m为实数），故④符合题意．‎ 综上，正确结论的个数有4个．‎ 故答案为：D．‎ ‎【分析】由抛物线的对称轴公式即可对②进行判断；由抛物线的开口方向可判断a，结合抛物线的对称轴可判断b，根据抛物线与y轴的交点可判断c，进而可判断①；由图象可得：当x=3时，y＞0，即9a+3b+c＞0，结合②的结论可判断③；由于当x=1时，二次函数y取最小值a+b+c，即 （m为实数），进一步即可对④进行判断，从而可得答案．‎ ‎10.【答案】 D ‎ ‎【解析】【解答】解：抛物线y＝ax2＋bx＋c过点A（−4，0），对称轴为直线x＝−1， ‎ 因此有：x＝−1＝− ，即2a−b＝0，因此选项D不符合题意；‎ 当x＝−1时，y＝a−b＋c的值最大，选项A符合题意；‎ 由抛物线的对称性可知，抛物线与x轴的另一个交点为（2，0），‎ 当x＝1时，y＝a＋b＋c＞0，因此选项B符合题意；‎ 抛物线与x轴有两个不同交点，因此b2−4ac＞0，C符合题意；‎ 故答案为：D．‎ ‎【分析】根据抛物线的开口方向、对称轴、顶点坐标、与x轴、y轴的交点以及过特殊点时相应的系数a、b、c满足的关系进行综合判断即可．‎ ‎11.【答案】 B ‎ ‎【解析】【解答】∵开口向下，与y轴交点在正半轴 ‎ ‎∴ ‎ ‎∵ 两点的横坐标分别为-1和1‎ ‎∴ ‎ ‎∴ ‎ ‎∴ ，故A选项不符合题意，B选项符合题意 ‎∵ 两点的横坐标分别为-1和1‎ ‎∴B点横坐标为3‎ ‎∴当 时 ，故C选项不符合题意 ‎∵当 时， 随 的增大而减小 ‎∴当 时， 随 的增大而减小，故D选项不符合题意 故答案为：B.‎ ‎【分析】根据开口方向、对称轴、与y轴交点即可分别判断 符号，进而判断A选项；由 两点的横坐标分别为-1和1可得两个方程，判断B选项；由当 时 判断C选项；由二次函数对称轴及增减性判断D选项.‎ ‎12.【答案】 A ‎ ‎【解析】【解答】解：①由图象可知：a＞0，c＜0， ‎ ‎∵- =1，‎ ‎∴b=-2a＜0，‎ ‎∴abc＞0，故①不符合题意；‎ ‎②∵抛物线与x轴有两个交点，‎ ‎∴b2-4ac＞0，故②符合题意；‎ ‎③当x=2时，y=4a+2b+c＜0，故③不符合题意；‎ ‎④当x=-1时，y=a-b+c=a-（-2a）+c＞0，‎ ‎∴3a+c＞0，故④符合题意；‎ ‎⑤当x=1时，y取到值最小，此时，y=a+b+c，‎ 而当x=m时，y=am2+bm+c，‎ 所以a+b+c≤am2+bm+c，‎ 故a+b≤am2+bm，即a+b≤m（am+b），故⑤符合题意，‎ ‎⑥当x＜-1时，y随x的增大而减小，故⑥不符合题意，‎ 故答案为：A．‎ ‎【分析】由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．‎ ‎13.【答案】 D ‎ ‎【解析】【解答】解：∵抛物线开口向上， ‎ ‎∴a＞0，‎ ‎∵抛物线的对称轴为直线x＝﹣ ＝1，‎ ‎∴b＝﹣2a＜0，‎ ‎∴ab＜0，所以A选项的结论正确；‎ ‎∵抛物线的对称轴为直线x＝1，抛物线与x轴的一个交点坐标在（0，0）与（﹣1，0）之间，‎ ‎∴抛物线与x轴的另一个交点坐标在（2，0）与（3，0）之间，‎ ‎∴一元二次方程ax2+bx+c＝0的正实数根在2和3之间，所以B选项的结论正确；‎ 把B（0，﹣2），A（﹣1，m）代入抛物线得c＝﹣2，a﹣b+c＝m，‎ 而b＝﹣2a，‎ ‎∴a+2a﹣2＝m，‎ ‎∴a＝ ，所以C选项的结论正确；‎ ‎∵点P1（t，y1），P2（t+1，y2）在抛物线上，‎ ‎∴当点P1、P2都在直线x＝1的右侧时，y1＜y2 ， 此时t≥1；‎ 当点P1在直线x＝1的左侧，点P2在直线x＝1的右侧时，y1＜y2 ， 此时0＜t＜1且t+1﹣1＞1﹣t，即 ＜t＜1，‎ ‎∴当 ＜t＜1或t≥1时，y1＜y2 ， 所以D选项的结论错误；‎ 故答案为：D.‎ ‎【分析】由抛物线开口方向得到a＞0，利用抛物线的对称轴方程得到b＝−2a＜0，则可对A选项进行判断；利用抛物线的对称性得到抛物线与x轴的另一个交点坐标在（2，0）与（3，0）之间，则根据抛物线与x轴的交点问题可对B选项进行判断；把B（0，−2），A（−1，m）和b＝−2a代入抛物解析式可对C选项进行判断；利用二次函数的增减性对D进行判断.‎ ‎14.【答案】 C ‎ ‎【解析】【解答】解：依题意得： = ， = ， ‎ 把 = ， = 代入 得 ‎ 当 时， ‎ 故小球达到的离地面的最大高度为： ‎ 故答案为：C ‎【分析】将 = ， = 代入 ，利用二次函数的性质求出最大值，即可得出答案．‎ ‎15.【答案】 C ‎ ‎【解析】【解答】解：A、将二次函数 向上平移10个单位，再向左平移2个单位后， ‎ 表达式为： = ，‎ 若过点（4，5），‎ 则 ，解得：a=-5，不符合题意；‎ B、∵ ，开口向上，‎ ‎∴当 时，y有最小值 ，不符合题意；‎ C、当x=2时，y=a+16，最小值为a-9，a+16-（a-9）=25，即 对应的函数值比最小值大25，符合题意；‎ D、△= =9-a，当a＜0时，9-a＞0，即方程 有两个不同的实数根，即二次函数图象与x轴有两个不同的交点，不符合题意，‎ 故答案为：C.‎ ‎【分析】求出二次函数平移之后的表达式，将（4，5）代入，求出a即可判断A；将函数表达式化为顶点式，即可判断B；求出当x=2时的函数值，减去函数最小值即可判断C；写出函数对应方程的根的判别式，根据a值判断判别式的值，即可判断D.‎ ‎16.【答案】 C ‎ ‎【解析】【解答】将(3,0.8)(4,0．9)(5,0.6)代入 得: ‎ ‎②－①和③－②得 ‎ ‎⑤－④得 ,解得a=﹣0.2．‎ 将a=﹣0.2．代入④可得b=1.5．‎ 对称轴= ．‎ 故答案为：C．‎ ‎【分析】图中三个坐标代入函数关系式解出a和b,再利用对称轴公式求出即可．‎ ‎17.【答案】 B ‎ ‎【解析】【分析】根据函数图象确定a、b、c的符号判断A；根据抛物线与x轴的交点判断B；利用抛物线的对称轴得到b=2a，再根据抛物线的对称性求得c=-3a即可判断C；利用抛物线的顶点坐标判断抛物线与直线y=n+1即可判断D．‎ ‎18.【答案】 C ‎ ‎【解析】【解答】把函数 的图象向右平移1个单位长度，平移后图象的函数解析式为 ‎ ‎，‎ 故答案为：C．‎ ‎【分析】抛物线在平移时开口方向不变，a不变，根据图象平移的口诀“左加右减、上加下减”即可解答．‎ ‎19.【答案】 B ‎ ‎【解析】【解答】解：根据题意，则 ， ， ‎ ‎∵ ，‎ ‎∴ ，‎ ‎∴ ，故①不符合题意；‎ 由抛物线与x轴有两个交点，则 ，故②符合题意；‎ ‎∵ ，‎ 令 时， ，‎ ‎∴ ，故③符合题意；‎ 在 中，‎ 令 时，则 ，‎ 令 时， ，‎ 由两式相加，得 ，故④符合题意；‎ ‎∴正确的结论有：②③④，共3个；‎ 故答案为：B．‎ ‎【分析】由抛物线的性质和对称轴是 ，分别判断a、b、c的符号，即可判断①；抛物线与x轴有两个交点，可判断②；由 ，得 ，令 ，求函数值，即可判断③；令 时，则 ，令 时， ，即可判断④；然后得到答案．‎ ‎20.【答案】 B ‎ ‎【解析】【解答】解：①∵抛物线开口向上与y轴交于负半轴， ‎ ‎∴a＞0,c＜0‎ ‎∴ac＜0‎ 故①正确；②∵抛物线的对称轴是x=1，‎ ‎∴ ‎ ‎∴b=-2a ‎∵当x=-1时，y=0‎ ‎∴0=a-b+c ‎∴3a+c=0‎ 故②正确；③∵抛物线与x轴有两个交点，即一元二次方程 有两个不相等的实数解 ‎∴ ‎ ‎∴ ‎ 故③正确；④当-1＜x＜1时，y随x的增大而减小，当x＞1时y随x的增大而增大.‎ 故④错误 所以正确的答案有①、②、③共3个 故答案为：B ‎【分析】根据抛物线的开口向上，得到a＞0，由于抛物线与y轴交于负半轴，得到c＜0，于是得到ac＜0，故①正确；根据抛物线的对称轴为直线x＝− ，于是得到2a＋b＝0，当x=-1时，得到 故②正确；把x＝2代入函数解析式得到4a＋2b＋c＜0，故③错误；抛物线与x轴有两个交点，也就是它所对应的方程有两个不相等的实数根，即可得出③正确根据二次函数的性质当x＞1时，y随着x的增大而增大，故④错误.‎ ‎21.【答案】 B ‎ ‎【解析】【解答】∵抛物线开口向上， ‎ ‎∴a>0，‎ ‎∵对称轴在y轴右边，‎ ‎∴ ，即b<0 ，‎ ‎∵抛物线与 轴的交点在 轴的下方，‎ ‎∴ ，‎ ‎∴ ，故①错误；‎ 对称轴在1左侧，∴ ‎ ‎∴-b<2a，即2a+b>0，故②错误；‎ 当x=-2时，y=4a-2b+c>0，故③正确；‎ 当x=-1时，抛物线过x轴，即a-b+c=0，‎ ‎∴b=a+c，‎ 又2a+b>0，‎ ‎∴2a+a+c>0，即3a+c>0，故④正确；‎ 故答案为：B.‎ ‎【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，进而判断①；根据对称轴<1求出2a与b的关系，进而判断②；根据x=﹣2时，y＞0可判断③；由x=-1和2a与b的关系可判断④.‎ ‎22.【答案】 B ‎ ‎【解析】【解答】二次函数 的图象经过 与 两点，即方程 的两个根是﹣3和1， ‎ ‎  可以看成二次函数y的图象沿着y轴平移m个单位,得到一个根3，‎ 由1到3移动2个单位，可得另一个根为﹣5.由于0＜n＜m，‎ 可知方程 的两根范围在﹣5~﹣3和1~3，‎ 由此判断B符合该范围.‎ 故答案为：B.‎ ‎【分析】由题意可得方程 的两个根是﹣3，1，方程在y的基础上加m，可以理解为二次函数的图象沿着y轴平移m个单位,由此判断加m后的两个根,即可判断选项.‎ ‎23.【答案】 C ‎ ‎【解析】【解答】解：由图象可得：a＞0，c＞0，△＝b2﹣4ac＞0，﹣ ＝﹣1， ‎ ‎∴b＝2a＞0，b2＞4ac ， 故A选项不合题意，‎ ‎∴abc＞0，故B选项不合题意，‎ 当x＝﹣1时，y＜0，‎ ‎∴a﹣b+c＜0，‎ ‎∴﹣a+c＜0，即a﹣c＞0，故C选项符合题意，‎ 当x＝m时，y＝am2+bm+c ， ‎ 当x＝﹣1时，y有最小值为a﹣b+c ， ‎ ‎∴am2+bm+c≥a﹣b+c ， ‎ ‎∴am2+bm≥a﹣b ， 故D选项不合题意，‎ 故答案为：C ． ‎ ‎【分析】根据二次函数的图象与系数的关系即可求出答案．‎ ‎24.【答案】 C ‎ ‎【解析】【解答】解：∵二次函数 的图像经过 ， ， ‎ ‎∴对称轴x= ，即x= ，‎ ‎∵对称轴x=b，‎ ‎∴ =b，化简得c=b-1，‎ ‎∵该二次函数的图象与x轴有公共点，‎ ‎∴△= ‎ ‎= ‎ ‎= ‎ ‎= ‎ ‎∴b=2，c=1，‎ ‎∴b+c=3，‎ 故答案为：C.‎ ‎【分析】根据二次函数 的图像经过 ， ，可得到二次函数的对称轴x= ，又根据对称轴公式可得x=b，由此可得到b与c的数量关系，然后由该二次函数的图象与x轴有公共点列出不等式解答即可 ‎25.【答案】 D ‎ ‎【解析】【解答】解：由图可知二次函数的图象的开向下，所以a<0,故A选项不符合题意； ‎ 因为二次函数的解析式为 ，‎ 所以图象的对称轴为直线 ，故B选项不符合题意；‎ 因为二次函数的对称轴为直线 ，A,B两点是抛物线与x轴的交点，‎ 所以A,B两点到对称轴的距离相等，‎ 设B点坐标为（b,0）,则有b-(-1)=(-1)-(-3),‎ 解得b=1,‎ 所以B点坐标为（-1,0）.‎ 故C选项不符合题意；‎ 由图形可知当x -1时,y随x的增大而增大，当-10.‎ 又∵ ，‎ ‎∴b<0.‎ ‎∵ ， ，‎ ‎∴ ,x1<0.‎ ‎∵点 ， 在该二次函数 的图象上 ‎∴ ， .‎ ‎∴y1-y2=2bx1>0.‎ ‎∴y1>y2.‎ 故答案为：B.‎ ‎【分析】首先分析出a,b,x1的取值范围，然后用含有代数式表示y1,y2 ， 再作差法比较y1,y2的大小.‎ ‎30.【答案】 D ‎ ‎【解析】【解答】∵抛物线开口向下， ‎ ‎∴a<0，‎ ‎∵对称轴x= =1>0，‎ ‎∴b=-2a，‎ ‎∴b>0，‎ ‎∵抛物线与y轴的交点在正半轴，‎ ‎∴c>0，‎ ‎∴abc<0，①不符合题意；‎ ‎∵b=-2a，‎ ‎∴b-2a=-2a-2a=-4a>0，②不符合题意；‎ 由图像可得当x=-1时，y=a-b+c<0，③不符合题意；‎ 当x=1时，y有最大值，y=a+b+c，‎ 当x=n时，y=an2+bn+c，‎ a+b+c>an2+bn+c，‎ 即a+b>n(an+b)，(n≠1)，④符合题意；‎ 当x=3时，函数值小于0，y=9a+3b+c<0，‎ ‎∵b=-2a，即a= ，‎ 代入9a+3b+c<0得9（ ）+3b+c<0，‎ ‎+c<0，‎ ‎-3b+2c<0，即2c<3b，⑤符合题意；‎ 故答案为：D．‎ ‎【分析】由图像判断出a<0，b>0，c>0，即可判断①；根据b=-2a可判断②；根据当x=-1时函数值小于0可判断③；根据当x=1时，y有最大值，y=a+b+c，当x=n时，y=an2+bn+c即可判断④；当x=3时，函数值小于0，y=9a+3b+c<0，且b=-2a，即a= ，代入9a+3b+c<0可判断⑤．‎ 二、填空题 ‎31.【答案】 且k≠1 ‎ ‎【解析】【解答】解：∵抛物线 与x轴有交点， ‎ ‎∴ ，‎ ‎∴ ，‎ 又∵ ，‎ ‎∴ ，‎ ‎∴k的取值范围是 且 ；‎ 故答案为： 且 .‎ ‎【分析】直接利用根的判别式进行计算，再结合 ，即可得到答案.‎ ‎32.【答案】 ‎ ‎【解析】【解答】解：在所列的5个数中任取一个数有5种等可能结果，其中使抛物线y=ax2+bx+c的开口向上的有3种结果， ‎ ‎∴使抛物线y=ax2+bx+c的开口向上的概率为 ，‎ 故答案为： .‎ ‎【分析】使抛物线y=ax2+bx+c的开口向上的条件是a＞0，据此从所列5个数中找到符合此条件的结果，再利用概率公式求解可得．‎ ‎33.【答案】 ②③④ ‎ ‎【解析】【解答】解：①由二次函数的图象开口向上可得a＞0，对称轴在y轴的右侧，b＜0， ‎ ‎∴ab＜0，故①不符合题意；‎ ‎②由图象可知抛物线与x轴的交点为（1，0），与y轴的交点为（0，﹣1），‎ ‎∴c＝﹣1，‎ ‎∴a+b﹣1＝0，故②符合题意；‎ ‎③∵a+b﹣1＝0，‎ ‎∴a﹣1＝﹣b，‎ ‎∵b＜0，‎ ‎∴a﹣1＞0，‎ ‎∴a＞1，故③符合题意；‎ ‎④∵抛物线与y轴的交点为（0，﹣1），‎ ‎∴抛物线为y＝ax2+bx﹣1，‎ ‎∵抛物线与x轴的交点为（1，0），‎ ‎∴ax2+bx﹣1＝0的一个根为1，根据根与系数的关系，另一个根为﹣ ，故④符合题意；‎ 故答案为②③④．‎ ‎【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点得出c的值，然后根据抛物线与x轴交点的个数及x＝1时二次函数的值的情况进行推理，进而对所得结论进行判断．‎ ‎34.【答案】 ‎ ‎【解析】【解答】解：根据表中x与y之间的数据，假设函数关系式为： ，并将表中(-1，0)、(0，3)、(1，4)三个点带入函数关系式，得： ‎ 解得： ，‎ ‎∴函数的表达式为： ．‎ 故答案为： ．‎ ‎【分析】根据表中x与y之间的数据，假设函数关系式为： ，并将表中的点(-1，0)、(0，3)、(1，4)、(3，0)任取三个点带入函数关系式，求出二次项系数、一次项系数、常数项即可求得答案．‎ ‎35.【答案】 y=x2+3． ‎ ‎【解析】【解答】抛物线y=x2向上平移3个单位得到y=x2+3． ‎ 故答案为：y=x2+3．‎ ‎【分析】直接根据抛物线向上平移的规律求解．‎ ‎36.【答案】 4 ‎ ‎【解析】【解答】∵A、B的纵坐标一样, ‎ ‎∴A、B是对称的两点,‎ ‎∴对称轴 ,即 ,‎ ‎∴b=﹣4．‎ ‎．‎ ‎∴抛物线顶点(2,﹣3)．‎ 满足题意n得最小值为4,‎ 故答案为4．‎ ‎【分析】通过A、B两点得出对称轴,再根据对称轴公式算出b,由此可得出二次函数表达式,从而算出最小值即可推出n的最小值．‎ ‎37.【答案】 (2，－5) ‎ ‎【解析】【解答】抛物线y=(x－1)2－5的顶点为（1，-5）， ‎ ‎∴关于y轴对称的坐标为（-1，-5），再向右平移3个单位长度后的坐标为（2，-5），‎ 故答案为：(2，－5)。‎ ‎【分析】先求出抛物线的顶点坐标，再根据题意进行变换即可求解．‎ ‎38.【答案】 （1,0）或（2,0）或（0,2） ‎ ‎【解析】【解答】解：将关联数为 代入函数 得到： ‎ ‎，‎ ‎∵关联数为 的函数图象与x轴有两个整交点（m为正整数），‎ ‎∴y=0，即 ，‎ 因式分解得 ，‎ 又∵关联数为 的函数图象与x轴有两个整交点，‎ 即 ‎ ‎∴m=1，‎ ‎∴ ，‎ 与x轴交点即y=0解得x=1或x=2，‎ 即坐标为 或 ，‎ 与y轴交点即x=0解得y=2，‎ 即坐标为 ，‎ ‎∴这个函数图象上整交点的坐标为 或 或 ；‎ 故答案为： 或 或 .‎ ‎【分析】将关联数为 代入函数 得到： ，由题意将y=0和x=0代入即可.‎ ‎39.【答案】 或 ‎ ‎【解析】【解答】解：对 ，当x=0时，y=3，∴点B坐标为（0，3）， ‎ 抛物线 的对称轴是直线： ，‎ 当∠ABM=90°时，如图1，过点M作MF⊥y轴于点F，则 ，‎ ‎∵∠1+∠2=90°，∠2+∠3=90°，‎ ‎∴∠1=∠3，‎ 又∠MFB=∠BOA=90°，‎ ‎∴△BFM∽△AOB，‎ ‎∴ ，即 ，解得：BF=3，‎ ‎∴OF=6，‎ ‎∴点M的坐标是（ ，6）；‎ 当∠BAM=90°时，如图2，过点A作EH⊥x轴，过点M作MH⊥EH于点H，过点B作BE⊥EH于点E，‎ 则 ，‎ 同上面的方法可得△BAE∽△AMH，‎ ‎∴ ，即 ，解得：AH=9，‎ ‎∴点M的坐标是（ ，﹣9）；‎ 综上，点M的坐标是 或 .‎ 故答案为： 或 .‎ ‎【分析】先求出点B的坐标和抛物线的对称轴，然后分两种情况讨论：当∠ABM=90°时，如图1，过点M作MF⊥y轴于点F，易证△BFM∽△AOB，然后根据相似三角形的性质可求得BF的长，进而可得点M坐标；当∠BAM=90°时，辅助线的作法如图2，同样根据△BAE∽△AMH求出AH的长，继而可得点M坐标.‎ ‎40.【答案】 ①②④ ‎ ‎【解析】【解答】 当 时，将二次函数 的图象先向右平移m个单位长度，再向上平移 个单位长度即可得到二次函数 的图象；当 时，将二次函数 的图象先向左平移 个单位长度，再向上平移 个单位长度即可得到二次函数 的图象 ‎ 该函数的图象与函数 的图象形状相同，结论①正确 对于 ‎ 当 时， ‎ 即该函数的图象一定经过点 ，结论②正确 由二次函数的性质可知，当 时，y随x的增大而增大；当 时，y随x的增大而减小 则结论③错误 的顶点坐标为 ‎ 对于二次函数 ‎ 当 时， ‎ 即该函数的图象的顶点 在函数 的图象上，结论④正确 综上，所有正确的结论序号是①②④‎ 故答案为：①②④.‎ ‎【分析】①两个二次函数可以通过平移得到，由此即可得两个函数的图象形状相同；②求出当 时，y的值即可得；③根据二次函数的增减性即可得；④先求出二次函数 的顶点坐标，再代入函数 进行验证即可得.‎ 三、综合题 ‎41.【答案】 （1） （2）解：当 时， ‎ 元 答：零售商一次性批发200件，需要支付18000元 ‎ （3）解：当 时 ‎ ‎，抛物线开口向下 当 时， 随 的增大而增大 又 为10的正整数倍 时， 最大，最大值是3800‎ 当 时， 随 的增大而减小 又 为10的正整数倍 时， 最大，最大值是3800‎ 当 时， ‎ 随 的增大而增大 时， 最大，最大值是3600‎ ‎∴当 或 时， 最大，最大值是3800‎ ‎【解析】【解答】解：（1）当100≤x≤300时，设 与 的函数关系式为y=kx+b，(k≠0)， ‎ 将点（100，100），（300，80）代入y=kx+b ，(k≠0)，‎ ‎ ，‎ 解，得 ‎ ‎  ‎ 故答案填： ‎ ‎【分析】（1）将两点（100，100），（300，80）代入到一次函数解析式，利用待定系数法即可求解；（2）将x=200代入到（1）求出y的值，最后求得答案；（3）当 时，求得y的最大值，当 求得y的最大值，最后作答.‎ ‎42.【答案】 （1）解：设一次函数表达式为 ， ‎ 将 代入，得 ‎ 解得 ‎ ‎.‎ ‎ （2）解：根据题意，得 ， ‎ 整理，得 ，‎ 解得 （不合题意，舍去）.‎ 答：该超市要想获得1000元的日销售利润，每千克樱桃的售价应定为30元.‎ ‎ （3）解：方法1： ‎ 设日销售利润为w元.‎ ‎.‎ ‎，‎ 抛物线开口向下，‎ 又 ，‎ 当 时，w随x的增大而增大.‎ 当 时，w有最大值， （元）.‎ 答：当每千克樱桃的售价定为40元时，可获得最大利润，最大利润是1600元.‎ 方法2：‎ 设日销售利润为w元.‎ ‎，‎ ‎，‎ 抛物线开口向下，对称轴为直线 .‎ 当 时，w随着x的增大而增大，‎ 当 时，w有最大值， （元）.‎ 答：当每千克樱桃的售价定为40元时，可获得最大利润，最大利润是1600元.‎ ‎【解析】【分析】（1）任选表中的两组对应数值，用待定系数法求一次函数的解析式即可；（2）销售利润=销售量 每千克所获得的利润，得 ，解出方程；（3）构造 ，利用二次函数的最大值问题解决.‎ ‎43.【答案】 （1）y=-x+120 （2）解： ‎ ‎ ‎ ‎ ‎ ‎，‎ ‎∴抛物线开口向下，函数有最大值 ‎∴当 时， ‎ 答：当销售单价是75元时，最大日利润是2025元.‎ ‎ （3）解： ‎ 当 时， ‎ 解得 ‎ ‎，∴有两种情况 ‎① 时，在对称轴左侧，w随x的增大而增大，‎ ‎∴当 时， ‎ ‎② 时，在 范围内 ，‎ ‎∴这种情况不成立， ‎ ‎【解析】【解答】解：（1）设解析式为 ， ‎ 将 和 代入，可得 ，解得 ，‎ 所以y与x的关系式为 ，‎ 所以答案为 ；‎ ‎【分析】（1）根据题中所给的表格中的数据，可以直接写出其关系式；（2）根据利润等于每件的利润乘以件数，再利用配方法求得其最值；（3）根据题意，列出关系式，再分类讨论求最值，比较得到结果.‎ ‎44.【答案】 （1）解：∵PD∥AB,AC=3,BC=4,CP=x, ‎ ‎∴ ,即 .‎ ‎∴ .‎ ‎∴AD= .‎ ‎ （2）解： . ‎ 对称轴为 ,二次函数开口向下,‎ ‎∴S随x增大而减小时x的取值为2≤x＜4.‎ ‎【解析】【分析】(1)由比例求出CD与CP的关系式,再求出AD.(2)把AD当作底,CP当作高,利用三角形面积公式求出S与x的函数表达式,再由条件求出范围即可.‎ ‎45.【答案】 （1）证明：∵四边形ABCD是正方形， ‎ ‎∴∠DCG=90°，‎ ‎∵CF平分∠DCG，‎ ‎∴∠FCG= ∠DCG=45°，‎ ‎∵∠G=90°，‎ ‎∴∠GCF=∠CFG=45°，‎ ‎∴FG=CG，‎ ‎∵四边形ABCD是正方形，EF⊥AE，‎ ‎∴∠B=∠G=∠AEF=90°，‎ ‎∴∠BAE+∠AEB=90°，∠AEB+∠FEG=90°，‎ ‎∴∠BAE=∠FEG，‎ ‎∵∠B=∠G=90°，‎ ‎∴△BAE∽△GEF；‎ ‎ （2）解：∵AB=BC=10，CE=2， ‎ ‎∴BE=8，‎ ‎∴FG=CG，‎ ‎∴EG=CE+CG=2+FG，‎ 由（1）知，△BAE∽△GEF，‎ ‎∴ ，‎ ‎∴ ，‎ ‎∴FG=8，‎ ‎∴S△ECF= CE•FG= ×2×8=8；‎ ‎ （3）解：设CE=x，则BE=10-x， ‎ ‎∴EG=CE+CG=x+FG，‎ 由（1）知，△BAE∽△GEF，‎ ‎∴ ，‎ ‎∴ ，‎ ‎∴FG=10-x，‎ ‎∴S△ECF= ×CE×FG= ×x•（10-x）= ，‎ 当x=5时，S△ECF最大= ，‎ ‎∴当EC=5时， 的面积最大.‎ ‎【解析】【分析】（1）先判断出CG=FG，再利用同角的余角相等，判断出∠BAE=∠FEG，进而得出△ABE∽△EGF，即可得出结论；（2）先求出BE=8，进而表示出EG=2+FG，由△BAE∽△GEF，得出 ，求出FG，最后用三角形面积公式即可得出结论；（3）同（2）的方法，即可得出S△ECF= ，即可得出结论.‎ ‎46.【答案】 （1）解：∵抛物线y＝x2−2mx＋m2＋2m−1过点B（3，5）， ‎ ‎∴把B（3，5）代入y＝x2−2mx＋m2＋2m−1，整理得，m2−4m＋3＝0，‎ 解得m1＝1，m2＝3，‎ 当m＝1时，y＝x2−2x＋2＝（x−1）2＋1，‎ 其顶点A的坐标为（1，1）；‎ 当m＝3时，y＝x2−6x＋m2＋14＝（x−3）2＋5，‎ 其顶点A的坐标为（3，5）；‎ 综上，顶点A的坐标为（1，1）或（3，5）；‎ ‎ （2）解：∵y＝x2−2mx＋m2＋2m−1＝（x−m）2＋2m−1， ‎ ‎∴顶点A的坐标为（m，2m−1），‎ ‎∵点A的坐标记为（x，y），‎ ‎∴x＝m，‎ ‎∴y＝2x−1；‎ ‎ （3）解：由（2）可知，抛物线的顶点在直线y＝2x−1上运动，且形状不变， ‎ 由（1）知，当m＝1或3时，抛物线过B（3，5），‎ 把C（0，2）代入y＝x2−2mx＋m2＋2m−1，得m2＋2m−1＝2，‎ 解得m＝1或−3，‎ 所以当m＝1或−3时，抛物线经过点C（0，2），‎ 如图所示，当m＝−3或3时，抛物线与线段BC只有一个交点（即线段CB的端点），‎ 当m＝1时，抛物线同时过点B、C，不合题意，‎ 所以m的取值范围是−3≤m≤3且m≠1．‎ ‎【解析】【分析】（1）根据待定系数法求得解析式，然后把解析式化成顶点式即可求得；（2）化成顶点式，求得顶点坐标，即可得出y与x的函数表达式；（3）把C（0，2）代入y＝x2−2mx＋m2＋2m−1，求得m＝1或−3，结合（1）根据图象即可求得．‎ ‎47.【答案】 （1）解：由题意得： ‎ y=500-10（x-50）=1000-10x，‎ W=（x-40）（1000-10x）=-10x2+1400x-40000；‎ ‎ （2）解：由题意得：-10x2+1400x-40000=8000， ‎ 解得：x1=60，x2=80，‎ 当x=60时，成本=40×[500-10（60-50）]=16000＞10000不符合要求，舍去，‎ 当x=80时，成本=40×[500-10（80-50）]=8000＜10000符合要求，‎ ‎∴销售价应定为每件80元；‎ ‎ （3）解：W=-10x2+1400x-40000， ‎ 当x=70时，W取最大值9000，‎ 故销售价定为每件70元时会获得最大利润9000元．‎ ‎【解析】【分析】（1）根据题意一个月能售出500件，若销售单价每涨1元，每周销量就减少10件，可得y=500-10（x-50），再利用一个月的销售量×每件销售利润=一个月的销售利润列出一个月的销售利润为W，写出W与x的函数关系式；（2）令W=8000，求出x的取值即可；（3）根据二次函数最值的求法求解即可．‎ ‎48.【答案】 （1）解：对于抛物线 ‎ 当 时， ，解得 或 ‎ 点A在x轴的负半轴上，‎ ‎∴点 ‎ ‎∵点 是抛物线 的最高点 ‎∴抛物线 的对称轴为 ，即 ‎ 解得 ‎ 把 代入 得： ‎ 解得 ‎ 则抛物线 的解析式为 ‎ 设点B的坐标为 ‎ 则 ，解得 或 ‎ ‎∵ ‎ ‎∴ ‎ 答：抛物线 的解析式为 ，点B的坐标为 ；‎ ‎ （2）解：设点C的坐标为 ，则点D的坐标为 ‎ 由题意得： ‎ 整理得： ‎ 由二次函数的性质可知，当 时，CD随a的增大而增大；当 时，CD随a的增大而减小 则当 时，CD取得最大值，最大值为5‎ ‎， 轴 边CD上的高为 ‎ 则 .‎ ‎【解析】【分析】（1）先求出点A的坐标，再根据“点A为抛物线 的最高点”可求出b的值，然后将点A代入 可求出c的值，从而可得抛物线 的解析式，最后设点B的坐标为 ，代入 可得一个关于m、n的方程组，求解即可得； （2）设点C的坐标为 ，从而可得点D的坐标和a的取值范围，再利用二次函数的性质求出CD的最大值，然后根据三角形的面积公式即可得.‎ ‎49.【答案】 （1）解：由题意得：y＝80+20× ， ‎ ‎∴y＝﹣40x+880；‎ ‎ （2）解：设每天的销售利润为w元，则有： ‎ w＝（﹣40x+880）（x﹣16）‎ ‎＝﹣40（x﹣19）2+360，‎ ‎∵a＝﹣40＜0，‎ ‎∴二次函数图象开口向下，‎ ‎∴当x＝19时，w有最大值，最大值为360元.‎ 答：当销售单价为19元时，销售这款“免洗洗手液”每天的销售利润最大，最大利润为880元.‎ ‎【解析】【分析】（1）销售单价为x（元），销售单价每降低0.5元，则每天可多售出20瓶（销售单价不低于成本价），则 为降低了多少个0.5元，再乘以20即为多售出的瓶数，然后加上80即可得出每天的销售量y； （2）设每天的销售利润为w元，根据利润等于每天的销售量乘以每瓶的利润，列出w关于x的函数关系式，将其写成顶点式，按照二次函数的性质可得答案.‎ ‎50.【答案】 （1）解：设y与x之间的函数表达式为 （ ），将表中数据（55，70）、（60，60）代入得： ‎ ‎，‎ 解得： ，‎ ‎∴y与x之间的函数表达式为 ；‎ ‎ （2）解：由题意得： ， ‎ 整理得 ，‎ 解得 ，‎ 答：为保证某天获得600元的销售利润，则该天的销售单价应定为60元/千克或80元/千克；‎ ‎ （3）解：设当天的销售利润为w元，则： ‎ ‎，‎ ‎∵﹣2＜0，‎ ‎∴当 时，w最大值=800.‎ 答：当销售单价定为70元/千克时，才能使当天的销售利润最大，最大利润是800元.‎ ‎【解析】【分析】（1）利用待定系数法来求一次函数的解析式即可； （2）根据单件的利润乘以销售的数量=总利润可列出关于销售单价x的方程，然后解一元二次方程即可； （3）利用每件的利润乘以销售量可得总利润，然后根据二次函数的性质来进行计算即可.‎