2021中考数学复习微专题 《中心对称》概念辨析与专项提升练习 7页

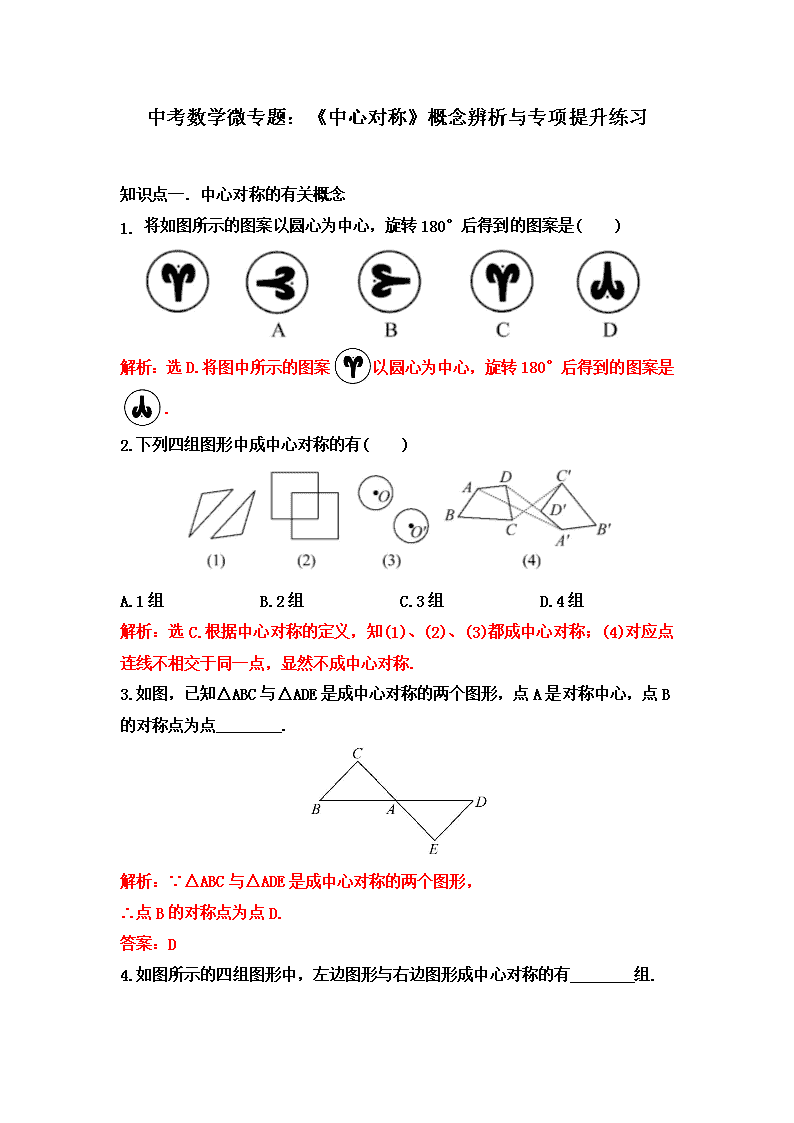
中考数学微专题：《中心对称》概念辨析与专项提升练习 知识点一．中心对称的有关概念 1. 将如图所示的图案以圆心为中心，旋转 180°后得到的图案是( ) 解析：选 D.将图中所示的图案 以圆心为中心，旋转 180°后得到的图案是 . 2.下列四组图形中成中心对称的有( ) A.1 组 B.2 组 C.3 组 D.4 组 解析：选 C.根据中心对称的定义，知(1)、(2)、(3)都成中心对称；(4)对应点 连线不相交于同一点，显然不成中心对称. 3.如图，已知△ABC 与△ADE 是成中心对称的两个图形，点 A 是对称中心，点 B 的对称点为点________. 解析：∵△ABC 与△ADE 是成中心对称的两个图形， ∴点 B 的对称点为点 D. 答案：D 4.如图所示的四组图形中，左边图形与右边图形成中心对称的有________组. 解析：根据中心对称的概念可得，成中心对称图形的有(1)(2)(3)，共 3 组. 答案：3 【知识总结】中心对称和轴对称的区别与联系 轴对称 中心对称 有一条对称轴——直线 有一个对称中心——点 图形沿对称轴对折(翻折 180°)后重合 图形绕对称中心旋转 180°后重合 折叠后与另一图形重合 旋转后与另一图形重合 对称点的连线被对称轴垂直平分 对称点连线经过对称中心，且被对 称中心平分 知识点二：中心对称的性质 1.如图，线段 AB 和 CD 关于点 O 成中心对称，若∠B=40°，则∠D 的度数为 ________. 解析：∵线段 AB 和 CD 关于点 O 成中心对称，∠B=40°， ∴△ABO≌△CDO， ∴∠B=∠D， ∴∠D 的度数为 40°. 答案：40° 知识总结： 掌握中心对称性质的“三个对应” 1.对应边相等. 2.对应边平行或在同一直线上. 3.对应角相等. 2.在直角坐标系中，点 B 的坐标为(3，1)，则点 B 关于原点成中心对称的点的 坐标为( ) A.(3，-1) B.(-3，1) C.(-1，-3) D.(-3，-1) 解析：选 D.点(3，1)关于原点成中心对称的点的坐标是(-3，-1). 3.在平面直角坐标系中，点 P(1，1)，N(2，0)，△MNP 和△M1N1P1 的顶点都在格 点上，△MNP与△M1N1P1关于某一点成中心对称，则对称中心的坐标为__________. 解析：∵点 P(1，1)，N(2，0)，∴由图形可知 M(3，0)，M1(1，2)，N1(2，2)， P1(3，1)，∵关于中心对称的两个图形，对应点的连线都经过对称中心，并且被 对称中心平分，∴对称中心的坐标为(2，1). 答案：(2，1) 4.如图，已知△AOB 与△DOC 中心对称，△AOB 的面积是 12，AB=3，则△DOC 中 CD 边上的高是________. 解析：∵△AOB 与△DOC 中心对称， ∴CD=AB=3， 且 S△DOC=S△AOB， 即 S△DOC=12， 设 CD 边上的高为 x， 则 3x÷2=12，解得 x=8. 答案：8 知识点三：画一个图形关于某一点的对称图形 1.在△ABC 中，A(-1，2)，B(-3，1)，C(0，-1).若将△ABC 绕点 C 顺时针旋转 180°后得到△A′B′C′，则 A 点的对应点 A′的坐标是( ) A.(2，-3) B.(1，-3) C.(2，-4) D.(1，-4) 解析：选 D.如图，A 点的对应点 A′的坐标是(1，-4). 2.画出与线段 AB 关于点 O 成中心对称的图形. 解析：作法：(1)如图，连接 AO，在 AO 的延长线上截取 OA′=OA，即可以求得 点 A 关于点 O 的对称点 A′. (2)同理，可以求得点 B 关于点 O 的对称点 B′. (3)连接 A′B′，就可以得到与 AB 关于点 O 对称的 A′B′. 3.如图，已知四边形 ABCD 以及点 O. 求作：四边形 A′B′C′D′，使得四边形 A′B′C′D′与四边形 ABCD 关于点 O 成中心对称. 解析：如图，四边形 A′B′C′D′为所作. 练习反馈： 1.如图，D 是△ABC 边 BC 的中点，连接 AD 并延长到点 E，使 DE=AD，连接 BE. (1)图中哪两个图形成中心对称？ (2)若△ADC 的面积为 4，求△ABE 的面积. 2.如图，已知△ABC 和△BDE 都是等腰直角三角形，∠ACB=∠BDE=90°，P 是 AE 的中点，连接 PC，PD. (1)在图中画出△PAC 关于点 P 成中心对称的图形. (2)判断 PC 与 PD 的关系，并证明你的结论. 3.如图，正方形 ABCD 与正方形 A1B1C1D1 关于某点中心对称，已知 A，D1，D 三点 的坐标分别是(0，4)，(0，3)，(0，2). (1)求对称中心的坐标. (2)写出顶点 B，C，B1，C1 的坐标. 4. 如图，在边长均为 1 的正方形网格纸上有一个△ABC，顶点 A，B，C 及点 O 均在格点上，请按要求完成以下操作或运算： (1)将△ABC 向上平移 4 个单位，得到△A1B1C1(不写作法，但要标出字母). (2)将△ABC 绕点 O 旋转 180°，得到△A2B2C2(不写作法，但要标出字母).