2019年福建省龙岩市长汀县中考数学一模试卷（含答案解析） 23页

2019 年福建省龙岩市长汀县中考数学一模试卷 一．选择题（共 10 小题，满分 40 分，每小题 4 分） 1．下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是（　　） A． B． C． D． 2．十九大报告指出，我国目前经济保持了中高速增长，在世界主要国家中名列前茅，国内生产总值 从 54 万亿元增长 80 万亿元，稳居世界第二，其中 80 万亿用科学记数法表示为（　　） A．8×1012 B．8×1013 C．8×1014 D．0.8×1013 3．下列运算正确的是（　　） A．（﹣a2）3＝a6 B．3a2•a＝3a2 C．﹣2a+a＝﹣a D．6a6÷2a2＝3a3 4．如图，在△ABC 中，∠C＝90°，EF∥AB，∠1＝33°，则∠A 的度数为（　　） A．57° B．47° C．43° D．33° 5．已知一次函数 y＝（m﹣1）x 的图象上两点 A（x1，y1），B（x2，y2），当 x1＞x2 时，有 y1＜y2， 那么 m 的取值范围是（　　） A．m＞0 B．m＜0 C．m＞1 D．m＜1 6．如图，在 Rt△ABC 中，CD 是斜边 AB 上的中线，已知 CD＝1.5，BC＝2，则 cosB 的值是（　　） A． B． C． D． 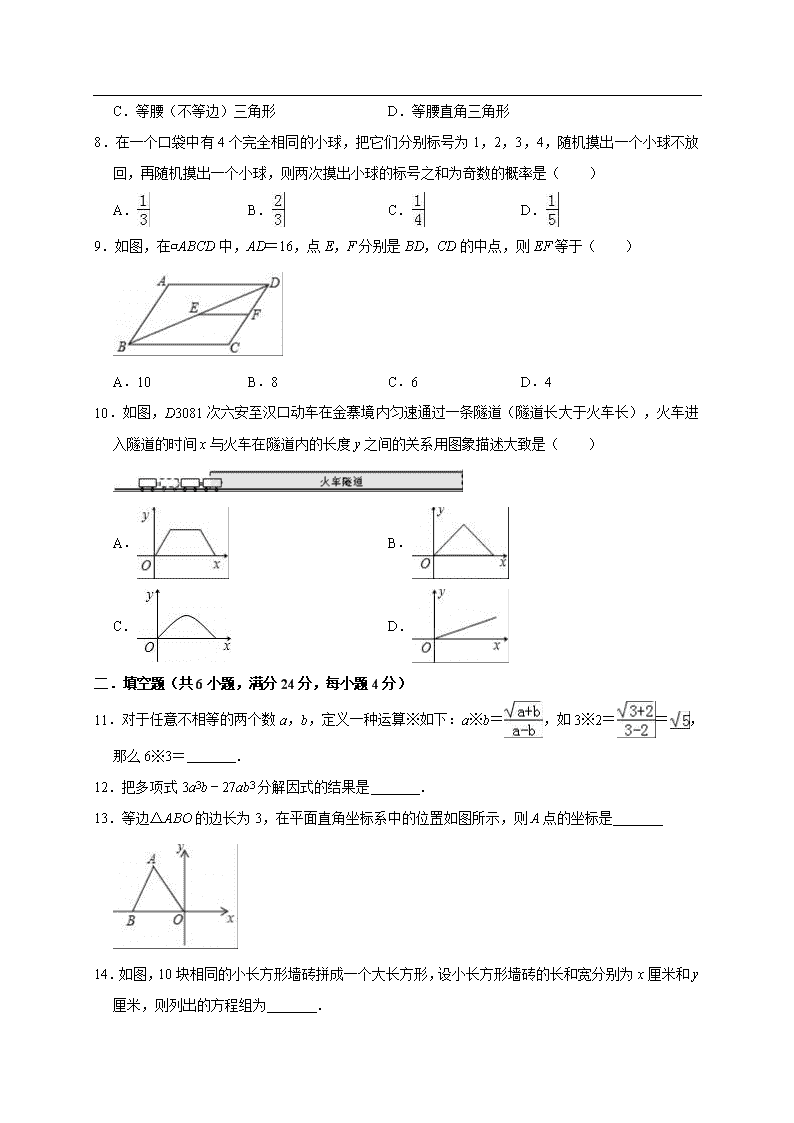7．在△ABC 中，∠A，∠B 均为锐角，且有|tanB﹣ |+（2cosA﹣1）2＝0，则△ABC 是（　　） A．直角（不等腰）三角形 B．等边三角形 C．等腰（不等边）三角形 D．等腰直角三角形 8．在一个口袋中有 4 个完全相同的小球，把它们分别标号为 1，2，3，4，随机摸出一个小球不放 回，再随机摸出一个小球，则两次摸出小球的标号之和为奇数的概率是（　　） A． B． C． D． 9．如图，在▱ABCD 中，AD＝16，点 E，F 分别是 BD，CD 的中点，则 EF 等于（　　） A．10 B．8 C．6 D．4 10．如图，D3081 次六安至汉口动车在金寨境内匀速通过一条隧道（隧道长大于火车长），火车进 入隧道的时间 x 与火车在隧道内的长度 y 之间的关系用图象描述大致是（　　） A． B． C． D． 二．填空题（共 6 小题，满分 24 分，每小题 4 分） 11．对于任意不相等的两个数 a，b，定义一种运算※如下：a※b＝ ，如 3※2＝ ＝ ， 那么 6※3＝　 　． 12．把多项式 3a3b﹣27ab3 分解因式的结果是　 　． 13．等边△ABO 的边长为 3，在平面直角坐标系中的位置如图所示，则 A 点的坐标是　 　 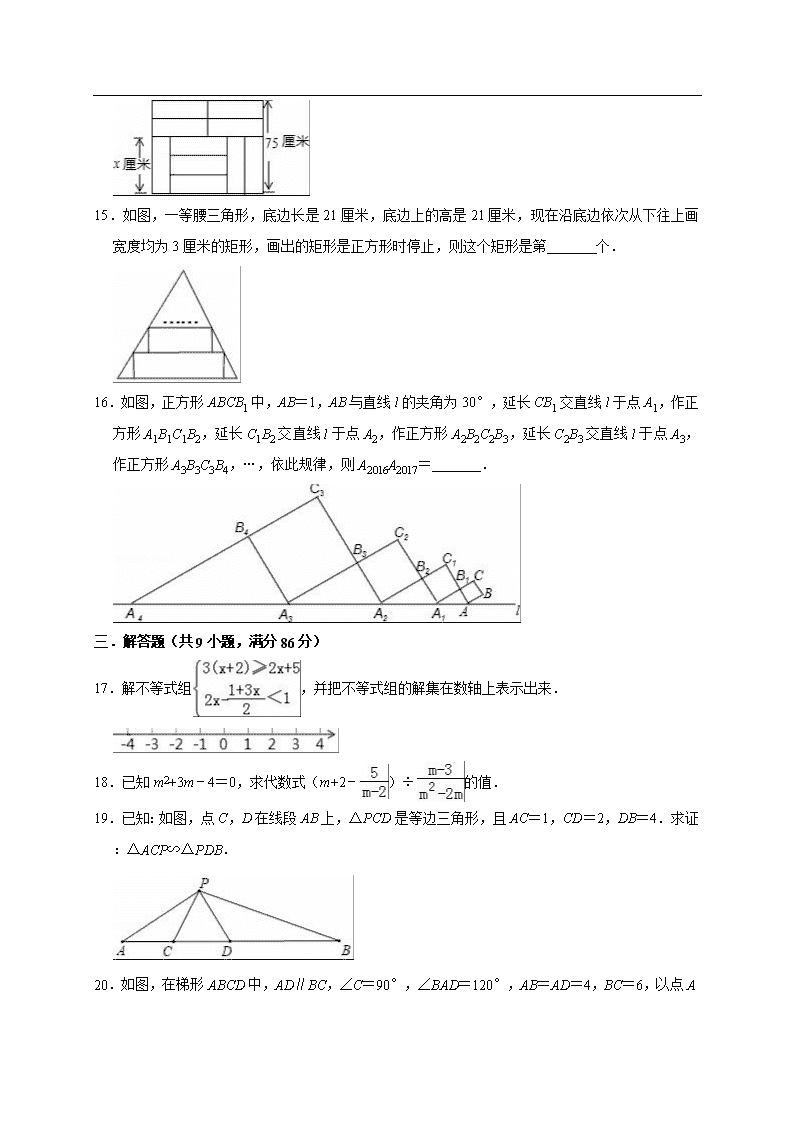14．如图，10 块相同的小长方形墙砖拼成一个大长方形，设小长方形墙砖的长和宽分别为 x 厘米和 y 厘米，则列出的方程组为　 　． 15．如图，一等腰三角形，底边长是 21 厘米，底边上的高是 21 厘米，现在沿底边依次从下往上画 宽度均为 3 厘米的矩形，画出的矩形是正方形时停止，则这个矩形是第　 　个． 16．如图，正方形 ABCB1 中，AB＝1，AB 与直线 l 的夹角为 30°，延长 CB1 交直线 l 于点 A1，作正 方形 A1B1C1B2，延长 C1B2 交直线 l 于点 A2，作正方形 A2B2C2B3，延长 C2B3 交直线 l 于点 A3， 作正方形 A3B3C3B4，…，依此规律，则 A2016A2017＝　 　． 三．解答题（共 9 小题，满分 86 分） 17．解不等式组 ，并把不等式组的解集在数轴上表示出来． 18．已知 m2+3m﹣4＝0，求代数式（m+2﹣ ）÷ 的值． 19．已知：如图，点 C，D 在线段 AB 上，△PCD 是等边三角形，且 AC＝1，CD＝2，DB＝4．求证 ：△ACP∽△PDB．[来源:学科网] 20．如图，在梯形 ABCD 中，AD∥BC，∠C＝90°，∠BAD＝120°，AB＝AD＝4，BC＝6，以点 A 为圆心在这个梯形内画出一个最大的扇形（图中阴影部分）． （1）求这个扇形的面积； （2）若将这个扇形围成圆锥，求这个圆锥的底面积． 21．一商店销售某种商品，平均每天可售出 20 件，每件盈利 40 元．为了扩大销售、增加盈利，该 店采取了降价措施，在每件盈利不少于 25 元的前提下，经过一段时间销售，发现销售单价每降 低 1 元，平均每天可多售出 2 件．[来源:学#科#网 Z#X#X#K] （1）若降价 3 元，则平均每天销售数量为　 　件； （2）当每件商品降价多少元时，该商店每天销售利润为 1200 元？ 22．“足球运球”是中考体育必考项目之一．兰州市某学校为了解今年九年级学生足球运球的掌握 情况，随机抽取部分九年级学生足球运球的测试成绩作为一个样本，按 A，B，C，D 四个等级进 行统计，制成了如下不完整的统计图．（说明：A 级：8 分﹣10 分，B 级：7 分﹣7.9 分，C 级：6 分﹣6.9 分，D 级：1 分﹣5.9 分） 根据所给信息，解答以下问题： （1）在扇形统计图中，C 对应的扇形的圆心角是　 　度； （2）补全条形统计图； （3）所抽取学生的足球运球测试成绩的中位数会落在　 　等级； （4）该校九年级有 300 名学生，请估计足球运球测试成绩达到 A 级的学生有多少人？ 23．如图，已知⊙O 是△ABC 的外接圆，且 AB＝BC＝CD，AB∥CD，连接 BD． （1）求证：BD 是⊙O 的切线； （2）若 AB＝10，cos∠BAC＝ ，求 BD 的长及⊙O 的半径． 24．如图，抛物线 y＝﹣ x2+bx+c（b 为常数）与 x 轴交于 A、C 两点，与 y 轴交于 B 点，直线 AB 的函数关系式为 y＝ x+ ． （1）求该抛物线的函数关系式与 C 点坐标； （2）已知点 M（m，0）是线段 OA 上的一个动点，过点 M 作 x 轴的垂线 l 分别与直线 AB 和抛 物线交于 D、E 两点，当 m 为何值时，△BDE 恰好是以 DE 为底边的等腰三角形？ （3）在（2）问条件下，当△BDE 恰好是以 DE 为底边的等腰三角形时，动点 M 相应位置记为点 M′，将 OM′绕原点 O 顺时针旋转得到 ON（旋转角在 0°到 90°之间）； ①探究：线段 OB 上是否存在定点 P（P 不与 O、B 重合），无论 ON 如何旋转， 始终保持不 变，若存在，试求出 P 点坐标；若不存在，请说明理由； ②试求出此旋转过程中，（NA+ NB）的最小值． 25．如图，AB 是⊙O 的直径， ＝ ，连结 AC，过点 C 作直线 l∥AB，点 P 是直线 l 上的一个动 点，直线 PA 与⊙O 交于另一点 D，连结 CD，设直线 PB 与直线 AC 交于点 E． （1）求∠BAC 的度数； （2）当点 D 在 AB 上方，且 CD⊥BP 时，求证：PC＝AC； （3）在点 P 的运动过程中 ①当点 A 在线段 PB 的中垂线上或点 B 在线段 PA 的中垂线上时，求出所有满足条件的∠ACD 的 度数； ②设⊙O 的半径为 6，点 E 到直线 l 的距离为 3，连结 BD，DE，直接写出△BDE 的面积． 2019 年福建省龙岩市长汀县中考数学一模试卷 参考答案与试题解析 一．选择题（共 10 小题，满分 40 分，每小题 4 分） 1．【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解． 【解答】解：A、是轴对称图形，不是中心对称图形，故本选项错误； B、既是轴对称图形，又是中心对称图形，故本选项正确； C、是轴对称图形，不是中心对称图形，故本选项错误； D、是轴对称图形，不是中心对称图形，故本选项错误．[来源:Zxxk.Com] 故选：B． 【点评】本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形 两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转 180 度后两部分重合． 2．【分析】科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为整数．确定 n 的值时， 要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对 值＞1 时，n 是正数；当原数的绝对值＜1 时，n 是负数． 【解答】解：80 万亿用科学记数法表示为 8×1013． 故选：B． 【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为 a×10n 的形式，其中 1≤|a| ＜10，n 为整数，表示时关键要正确确定 a 的值以及 n 的值． 3．【分析】根据幂的乘方、单项式与单项式的乘除运算法则、合并同类项法则逐一计算可得． 【解答】解：A、（﹣a2）3＝﹣a6，此选项错误； B、3a2•a＝3a3，此选项错误； C、﹣2a+a＝﹣a，此选项正确； D、6a6÷2a2＝3a4，此选项错误； 故选：C． 【点评】本题主要考查整式的运算，解题的关键是掌握幂的乘方、单项式与单项式的乘除运算法 则、合并同类项法则． 4．【分析】先根据平行线的性质求出∠B 的度数，再由直角三角形的性质求出∠A 的度数即可． 【解答】解：∵EF∥AB，∠1＝33°， ∴∠B＝∠1＝33°， ∵△ABC 中，∠C＝90°，∠B＝33°， ∴∠A＝90°﹣∠B＝90°﹣33°＝57°． 故选：A． 【点评】本题考查的是平行线的性质及直角三角形的性质，用到的知识点为：两直线平行，内错 角相等． 5．【分析】根据一次函数的增减性可求解． 【解答】解：∵一次函数 y＝（m﹣1）x 的图象上两点 A（x1，y1），B（x2，y2），且 x1＞x2 时， 有 y1＜y2 ∴m﹣1＜0 ∴m＜1 故选：D． 【点评】本题考查了一次函数图象上点的坐标特征，利用一次函数增减性解决问题是本题的关键 ． 6．【分析】根据直角三角形的性质求出 AB，根据余弦的定义计算即可． 【解答】解：∵Rt△ABC 中，CD 是斜边 AB 上的中线， ∴AB＝2CD＝3， 在 Rt△ABC 中，cosB＝ ＝ ， 故选：A． 【点评】本题考查的是解直角三角形、直角三角形的性质，掌握余弦的定义、直角三角形斜边上 的中线是斜边的一半是解题的关键． 7．【分析】直接利用特殊角的三角函数值得出∠B，∠A 的度数，进而得出答案． 【解答】解：∵|tanB﹣ |+（2cosA﹣1）2＝0， ∴tanB＝ ，2cosA＝1， 则∠B＝60°，∠A＝60°， ∴△ABC 是等边三角形． 故选：B． 【点评】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键． 8．【分析】先画树状图展示所有 12 种等可能的结果数，再找出其中两次摸出的小球的标号的和为 奇数的结果数，然后根据概率公式求解． 【解答】解：画树状图为： 共有 12 种等可能的结果数，其中两次摸出的小球的标号的和为奇数的结果数为 8， 所以两次摸出的小球的标号的和为奇数的概率为 ＝ ， 故选：B． 【点评】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果 n，再从 中选出符合事件 A 或 B 的结果数目 m，然后利用概率公式计算事件 A 或事件 B 的概率． 9．【分析】利用三角形的中位线定理即可解决问题； 【解答】解：∵四边形 ABCD 是平行四边形， ∴BC＝AD＝16， ∵点 E，F 分别是 BD，CD 的中点， ∴EF＝ BC＝8， 故选：B． 【点评】本题考查平行四边形的性质、三角形的中位线定理等知识，解题的关键是熟练掌握基本 知识，属于中考基础题． 10．【分析】先分析题意，把各个时间段内 y 与 x 之间的关系分析清楚，本题是分段函数，分为三 段． 【解答】解：根据题意可知火车进入隧道的时间 x 与火车在隧道内的长度 y 之间的关系具体可描 述为：当火车开始进入时 y 逐渐变大，火车完全进入后一段时间内 y 不变，当火车开始出来时 y 逐 渐变小，故反映到图象上应选 A． 故选：A． 【点评】本题考查了动点问题的函数图象，主要考查了根据实际问题作出函数图象的能力．解题 的关键是要知道本题是分段函数，分情况讨论 y 与 x 之间的函数关系． 二．填空题（共 6 小题，满分 24 分，每小题 4 分） 11．【分析】根据※的运算方法列式算式，再根据算术平方根的定义解答． 【解答】解：6※3＝ ＝1． 故答案为：1． 【点评】本题考查了算术平方根的定义，读懂题目信息，理解※的运算方法是解题的关键． 12．【分析】先提出公因式 3ab，再利用平方差公式进行因式分解． 【解答】解：原式＝3ab（a2﹣9b2）＝3ab（a+3b）（a﹣3b）． 故答案是：3ab（a+3b）（a﹣3b）． 【点评】本题考查了提公因式法和公式法进行分解因式，解决本题的关键是熟记提公因式法和公 式法． 13．【分析】过 A 作 AE⊥x 轴于 E，根据等边三角形性质求出 OE，根据勾股定理求出 AE，即可得 出答案． 【解答】解：过 A 作 AE⊥x 轴于 E， ∵△ABO 是等边三角形，边长为 3， ∴OA＝3，OE＝BE＝1.5， 在 Rt△AEO 中，由勾股定理得：AE＝ ＝ ＝1.5 ， 即点 A 的坐标为（﹣1.5，1.5 ）， 故答案为：（﹣1.5，1.5 ）． 【点评】本题考查了等边三角形的性质和勾股定理，能够正确作出辅助线是解此题的关键． 14．【分析】根据图示可得：长方形的长可以表示为 x+2y，长又是 75 厘米，故 x+2y＝75，长方形 的宽可以表示为 2x，或 x+3y，故 2x＝3y+x，整理得 x＝3y，联立两个方程即可． 【解答】解：根据图示可得 ， 故答案是： ． 【点评】此题主要考查了由实际问题抽象出二元一次方程组，关键是看懂图示，分别表示出长方 形的长和宽． 15．【分析】根据相似三角形的相似比求得顶点到这个正方形的长，再根据矩形的宽求得是第几张． 【解答】解：已知剪得的纸条中有一张是正方形，则正方形中平行于底边的边是 3， 所以根据相似三角形的性质可设从顶点到这个正方形的线段为 x， 则 ，解得 x＝3， 所以另一段长为 21﹣3＝18， 因为 18÷3＝6，所以是第 6 个． 故答案为：6 【点评】本题主要考查了相相似三角形的判定和性质，关键是根据似三角形的性质及等腰三角形 的性质的综合运用解答． 16．【分析】由四边形ABCB1 是正方形，得到 AB＝AB1，AB∥CB1，于是得到 AB∥A1C，根据平行 线的性质得到∠CA1A＝30°，解直角三角形得到 A1B1＝ ，AA1＝2，同理：A2A3＝2（ ）2， A3A4＝2（ ）3，找出规律 AnAn+1＝2（ ）n，答案即可求出． 【解答】解：∵四边形 ABCB1 是正方形， ∴AB＝AB1，AB∥CB1， ∴AB∥A1C， ∴∠CA1A＝30°， ∴A1B1＝ ，AA1＝2， ∴A1B2＝A1B1＝ ， ∴A1A2＝2 ， 同理：A2A3＝2（ ）2， A3A4 ＝2（ ）3， … ∴AnAn+1＝2（ ）n， ∴A2016A2017＝2（ ）2016＝2×31008． 故答案为：2×31008． 【点评】本题考查了正方形的性质，含30°直角三角形的性质，平行线的性质的综合应用，求出 后一个正方形的边长是前一个正方形的边长的 倍是解题的关键． 三．解答题（共 9 小题，满分 86 分） 17．【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、 大大小小无解了确定不等式组的解集． 【解答】解： ， 解不等式①，得：x≥﹣1， 解不等式②，得：x＜3， 则不等式组的解集为﹣1≤x＜3， 将不等式组的解集表示在数轴上如下： 【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取 大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键． 18．【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约 分得到最简结果，把已知等式变形后代入计算即可求出值． 【解答】解：原式＝ • ＝ • ＝m（m+3）＝m2+3m， ∵m2+3m﹣4＝0， ∴m2+3m＝4， ∴原式＝4． 【点评】此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键． 19．【分析】根据等边三角形的性质得到∠PCD＝∠PDC＝60°，PC＝CD＝PD＝2，得到∠PCA＝∠ PDB＝120°，根据已知条件得到 ＝ ，于是得到结论． 【解答】证明：∵△PCD 是等边三角形， ∴∠PCD＝∠PDC＝60°，PC＝CD＝PD＝2， ∴∠PCA＝∠PDB＝120°， ∵AC＝1，BD＝4， ∴ ， ＝ ， ∴ ＝ ， ∴△ACP∽△PDB． 【点评】本题考查了相似三角形的判定，等边三角形的性质，熟练掌握相似三角形的判定定理是 解题的关键． 20．【分析】（1）作 AE⊥BC，根据三角函数求得扇形的半径 AE，由梯形的性质得出圆心角度数， 继而根据扇形的面积公式可得． （2）根据圆锥的底面周长等于扇形的弧长，从而求得底面半径，从而求得面积． 【解答】解：（1）过点 A 作 AE⊥BC 于 E， 则 AE＝ABsinB＝4× ＝2 ， ∵AD∥BC，∠B＝60°， ∴∠BAD＝120°， ∴扇形的面积为 ＝4π， （2）设圆锥的底面半径为 r，则 2πr＝ ， 解得：r＝ 若 将这个扇形围成圆锥，这个圆锥的底面积 π． 【点评】本题要熟知切线的性质，直角梯形的性质和扇形弧长计算公式．利用切线的性质求得AE 的长即半径是解题的关键，注意扇形的周长为两条半径的长加上弧长． 21．【分析】（1）根据销售单价每降低 1 元，平均每天可多售出 2 件，可得若降价 3 元，则平均每 天可多售出 2×3＝6 件，即平均每天销售数量为 20+6＝26 件； （2）利用商品平均每天售出的件数×每件盈利＝每天销售这种商品利润列出方程解答即可． 【解答】解：（1）若降价 3 元，则平均每天销售数量为 20+2×3＝26 件． 故答案为 26； （2）设每件商品应降价 x 元时，该商店每天销售利润为 1200 元． 根据题意，得 （40﹣x）（20+2x）＝1200，[来源:学科网 ZXXK] 整理，得 x2﹣30x+200＝0， 解得：x1＝10，x2＝20． ∵要求每件盈利不少于 25 元， ∴x2＝20 应舍去， 解得：x＝10． 答：每件商品应降价 10 元时，该商店每天销售利润为 1200 元． 【点评】此题主要考查了一元二次方程的应用，利用基本数量关系：平均每天售出的件数×每件 盈利＝每天销售的利润是解题关键． 22．【分析】（1）先根据 B 等级人数及其百分比求得总人数，总人数减去其他等级人数求得 C 等 级人数，继而用 360°乘以 C 等级人数所占比例即可得； （2）根据以上所求结果即可补全图形； （3）根据中位数的定义求解可得； （4）总人数乘以样本中 A 等级人数所占比例可得． 【解答】解：（1）∵总人数为 18÷45%＝40 人， ∴C 等级人数为 40﹣（4+18+5）＝13 人， 则 C 对应的扇形的圆心角是 360°× ＝117°， 故答案为：117； （2）补全条形图如下： （3）因为共有 40 个数据，其中位数是第 20、21 个数据的平均数，而第 20、21 个数据均落在 B 等级， 所以所抽取学生的足球运球测试成绩的中位数会落在 B 等级， 故答案为：B． （4）估计足球运球测试成绩达到 A 级的学生有 300× ＝30 人． 【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得 到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接 反映部分占总体的百分比大小． 23．【分析】（1）如图 1，作直径 BE，半径 OC，证明四边形 ABDC 是平行四边形，得∠A＝∠D， 由等腰三角形的性质得：∠CBD＝∠D＝∠A＝∠OCE，可得∠EBD＝90°，所以 BD 是⊙O 的切 线； （2）如图 2，根据三角函数设 EC＝3x，EB＝5x，则 BC＝4x 根据 AB＝BC＝10＝4x，得 x 的值， 求得⊙O 的半径 为 ，作高线 CG，根据等腰三角形三线合一得 BG＝DG，根据三角函数可得结 论． 【解答】（1）证明：如图 1，作直径 BE，交⊙O 于 E，连接 EC、OC， 则∠BCE＝90°， ∴∠OCE+∠OCB＝90°， ∵AB∥CD，AB＝CD， ∴四边形 ABDC 是平行四边形， ∴∠A＝∠D， ∵OE＝OC， ∴∠E＝∠OCE， ∵BC＝CD， ∴∠CBD＝∠D， ∵∠A＝∠E， ∴∠CBD＝∠D＝∠A＝∠OCE， ∵OB＝OC， ∴∠OBC＝∠OCB， ∴∠OBC+∠CBD＝90°， 即∠EBD＝90°， ∴BD 是⊙O 的切线； （2）如图 2，∵cos∠BAC＝cos∠E＝ ， 设 EC＝3x，EB＝5x，则 BC＝4x， ∵AB＝BC＝10＝4x， x＝ ， ∴EB＝5x＝ ， ∴⊙O 的半径为 ， 过 C 作 CG⊥BD 于 G， ∵BC＝CD＝10， ∴BG＝DG， Rt△CGD 中，cos∠D＝cos∠BAC＝ ， ∴ ， ∴DG＝6， ∴BD＝12． 【点评】本题考查了圆周角定理、三角函数以及切线的判定．要证某线是圆的切线，已知此线过 圆上某点，连接圆心与这点（即为半径），再证垂直即可，在圆的有关计算中，常根据三角函数 的比设未知数，列方程解决问题． 24．【分析】（1）根据已知条件得到 B（0， ），A（﹣6，0），解方程组得到抛物线的函数关 系式为：y＝﹣ x2﹣ x+ ，于是得到 C（1，0）； （2）由点 M（m，0），过点 M 作 x 轴的垂线 l 分别与直线 AB 和抛物线交于 D、E 两点，得到 D （m， m+ ），当 DE 为底时，作 BG⊥DE 于 G，根据等腰三角形的性质得到 EG＝GD＝ ED ，GM＝OB＝ ，列方程即可得到结论； （3）①根据已知条件得到 ON＝OM′＝4，OB＝ ，由∠NOP＝∠BON，特殊的当△NOP∽△ BON 时，根据相似三角形的性质得到 ＝ ＝ ＝ ，于是得到结论； ②根据题意得到 N 在以 O 为圆心，4 为半径的半圆上，由①知， ＝ ＝ ，得到 NP＝ NB ，于是得到（NA+ NB）的最小值＝NA+NP，此时 N，A，P 三点共线，根据勾股定理得到结论． 【解答】解：（1）在 y＝ x+ 中，令 x＝0，则 y＝ ，令 y＝0，则 x＝﹣6， ∴B（0， ），A（﹣6，0）， 把 B（0， ），A（﹣6，0）代入 y＝﹣ x2+bx+c 得， ， ∴ ， ∴抛物线的函数关系式为：y＝﹣ x2﹣ x+ ， 令 y＝0，则 0＝﹣ x2﹣ x+ ， ∴x1＝﹣6，x2＝1， ∴C（1，0）； （2）∵点 M（m，0），过点 M 作 x 轴的垂线 l 分别与直线 AB 和抛物线交于 D、E 两点， ∴D（m， m+ ），当 DE 为底时， 如图 1，作 BG⊥DE 于 G，则 EG＝GD＝ ED，GM＝OB＝ ， ∵DM+DG＝GM＝OB， ∴ m+ + （﹣ m2﹣ m+ ﹣ m﹣ ）＝ ， 解得：m1＝﹣4，m2＝0（不合题意，舍去）， ∴当 m＝﹣4 时，△BDE 恰好是以 DE 为底边的等腰三角形； （3）①存在，如图 2． ∵ON＝OM′＝4，OB＝ ， ∵∠NOP＝∠BON， ∴当△NOP∽△BON 时， ＝ ＝ ＝ ， ∴ 不变， 即 OP＝ ON＝ ×4＝3， ∴P（0，3）； ②∵N 在以 O 为圆心，4 为半径的半圆上，由①知， ＝ ＝ ， ∴NP＝ NB， ∴（NA+ NB）的最小值＝NA+NP， ∴此时 N，A，P 三点共线， ∴（NA+ NB）的最小值＝ ＝3 ． 【点评】本题是二次函数综合题，其中涉及到待定系数法求抛物线的解析式，函数图象上点的坐 标特征，等腰三角形的性质，相似三角形的性质，勾股定理等知识，正确作出辅助线是解题的关 键． 25．【分析】（1）只要证明△ABC 是等腰直角三角形即可； （2）只要证明 CB＝CP，CB＝CA 即可；、 （3）①分四种情形分别画出图形一一求解即可； ②分两种情形如图 6 中，作 EK⊥PC 于 K．只要证明四边形 ADBC 是正方形即可解决问题；如图 7 中，连接 OC，作 BG⊥CP 于 G，EK⊥PC 于 K．由△AOQ∽△ADB，可得 S△ABD＝ ，可得 S△PBD＝S△ABP﹣S△ABD＝ ，再根据 S△BDE＝ •S△PBD 计算即可解决问题； 【解答】解：（1）如图 1 中，连接 BC． ∵ ＝ ， ∴BC＝CA， ∵AB 是直径， ∴∠ACB＝90°， ∴∠BAC＝∠CBA＝45°． （2）解：如图 1 中，设 PB 交 CD 于 K． ∵ ＝ ， ∴∠CDB＝∠CDP＝45°，CB＝CA， ∴CD 平分∠BDP，又∵CD⊥BP， ∴∠DKB＝∠DKP＝90°，∵DK＝DK， ∴△DKB≌△DKP， ∴BK＝KP， 即 CD 是 PB 的中垂线， ∴CP＝CB＝CA． （3）①（Ⅰ）如图 2，当 B 在 PA 的中垂线上，且 P 在右时，∠ACD＝15°； 理由：连接 BD、OC．作 BG⊥PC 于 G．则四边形 OBGC 是正方形， ∵BG＝OC＝OB＝CG， ∵BA＝BA， ∴PB＝2BG， ∴∠BPG＝30°， ∵AB∥PC， ∴∠ABP＝30°， ∵BD 垂直平分 AP， ∴∠ABD＝ ∠ABP＝15°， ∴∠ACD＝15° （Ⅱ）如图 3，当 B 在 PA 的中垂线上，且 P 在左，∠ACD＝105°； 理由：作 BG⊥CP 于 G． 同法可证∠BPG＝30°，可得∠APB＝∠BAP＝∠APC＝15°， ∴∠ABD＝75°， ∵∠ACD+∠ABD＝180°， ∴∠ACD＝105°； （Ⅲ）如图 4，A 在 PB 的中垂线上，且 P 在右时∠ACD＝60°； 理由：作 AH⊥PC 于 H，连接 BC． 同法可证∠APH＝30°，可得∠DAC＝75°，∠D＝∠ABC＝45°， ∴∠ACD＝60°； （Ⅳ）如图 5，A 在 PB 的中垂线上，且 P 在左时∠ACD＝120° 理由：作 AH⊥PC 于 H． 同法可证：∠APH＝30°，可得∠ADC＝45°，∠DAC＝60°﹣45°＝15°， ∴∠ACD＝120°． ②如图 6 中，作 EK⊥PC 于 K． ∵EK＝CK＝3，[来源:学。科。网] ∴EC＝3 ， ∵AC＝6 ， ∴AE＝EC， ∵AB∥PC， ∴∠BAE＝∠PCE，∵∠AEB＝∠PEC， ∴△ABE≌△CPE， ∴PC＝AB＝CD， ∴△PCD 是等腰直角三角形，可得四边形 ADBC 是正方形， ∴S△BDE＝ •S 正方形 ADBC＝36． 如图 7 中，连接 OC，作 BG⊥CP 于 G，EK⊥PC 于 K． 由题意 CK＝EK＝3，PK＝1，PG＝2， 由△AOQ∽△PCQ，可得 QC＝ ， PQ2＝ ， 由△AOQ∽△ADB，可得 S△ABD＝ ， ∴S△PBD＝S△ABP﹣S△ABD＝ ， ∴S△BDE＝ •S△PBD＝ 综上所，满足条件的△BDE 的面积为 36 或 ． 【点评】本题考查圆综合题、等腰直角三角形的性质和判定、相似三角形的判定和性质、切线的 性质、线段的垂直平分线的性质和判定、直角三角形中 30 度角的判定等知识，解题的关键是学 会用分类讨论的思想思考问题，学会添加常用辅助线，构造特殊三角形解决问题，属于中考压轴 题．