2020年四川省遂宁市中考数学试卷【含答案；word版本试题；可编辑】 11页

1 / 11 2020 年四川省遂宁市中考数学试卷 一、选择题（本大题共 10 个小题，每小题 4 分，共 40 分，在每个小题给出的四个选 项中，只有一个符合题目要求．） 1. . 的相反数是() A. . B. . C. . D. .2.已知某新型感冒病毒直径约为 ǤͲ 米，将 ǤͲ 用科学记数法表 示() A. ǤͲ B. ǤͲ C. ǤͲ D. ǤͲ 3.下列计算正确的是（） A. ᦙ䁡 .ᦙ ＝ Ͳ䁡 B. ᦙ 䁞 ᦙ Ͳ ＝ ᦙ Ͳ 䁞 ᦙͲC. ᦙ Ͳ 䁡 Ͳ ＝ ᦙ 䁡 Ͳ D. ᦙ Ͳ 䁡 䁡 ＝ ᦙ Ͳ4.下列图形中，既是轴对称图形，又是中心对称图形的是（） A.等边三角形 B.平行四边形 C.矩形 D.正五边形 5.函数 䁞Ͳ 中，自变量 的取值范围是（） A. Ͳ B. Ͳ C. Ͳ 且 D. Ͳ 且 6.关于 的分式方程 Ͳ Ͳ 有增根，则 的值（） A. ＝ Ͳ B. ＝ C. ＝ D. ＝ 7.如图，在平行四边形 馰ԯ댠 中， 馰ԯ 的平分线交 ԯ 于点 ，交 댠 于点 ，交 ԯ댠 的延长线于点 ，若 ＝ Ͳ댠 ，则 馰 的值为（） A. Ͳ B. C. Ͳ D. 8.二次函数 ＝ ᦙ Ͳ 䁞 䁡 䁞 ᦙ 的图象如图所示，对称轴为直线 ＝ ，下列结 论不正确的是（） A. 䁡 Ͳ ᦙ B. ᦙ䁡 C. ᦙ ܿ D. ᦙ Ͳ 䁞 䁡 ᦙ 䁡 （ 为任意实数） 9.如图，在 馰ԯ 中， ԯ ＝ ， ԯ ＝ 馰ԯ ，点 在 馰 上，经过点 的 与 馰ԯ 相切于点 댠 ，交 馰 于点 ，若 ԯ댠 Ͳ ，则图中阴影部分面积为（） A. Ͳ B. Ͳ Ͳ C. Ͳ D. 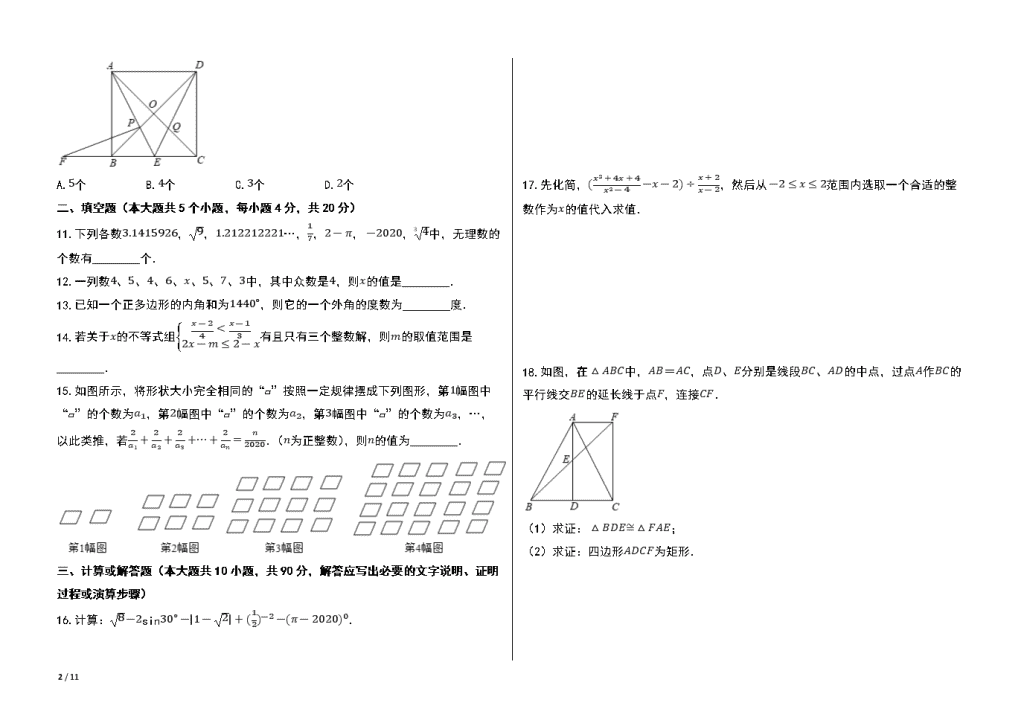10.如图，在正方形 馰ԯ댠 中，点 是边 馰ԯ 的中点，连接 、 댠 ，分别交 馰댠 、 ԯ 于点 、 ，过点 作 交 ԯ馰 的延长线于 ，下列结论： ① 댠 䁞 ԯ 䁞 댠馰 ＝ ， ② ＝ ， ③ Ͳ ， ④若四边形 的面积为 ，则该正方形 馰ԯ댠 的面积为 ， ⑤ ԯ ＝ 댠 ． 2 / 11 其中正确的结论有（） A. . 个 B. 个 C. 个 D. Ͳ 个 二、填空题（本大题共 5 个小题，每小题 4 分，共 20 分） 11.下列各数 Ǥ.Ͳ ， ， ǤͲͲͲͲͲͲ …， ， Ͳ ， ͲͲ ， 中，无理数 的个数有________个． 12.一列数 、 . 、 、 、 、 . 、 、 中，其中众数是 ，则 的值是________． 13.已知一个正多边形的内角和为 ，则它的一个外角的度数为________度． 14.若关于 的不等式组 Ͳ ܿ Ͳ Ͳ 有且只有三个整数解，则 的取值范围是 ________． 15.如图所示，将形状大小完全相同的“ ”按照一定规律摆成下列图形，第 幅图 中“ ”的个数为 ᦙ ，第 Ͳ 幅图中“ ”的个数为 ᦙͲ ，第 幅图中“ ”的个数为 ᦙ ，…，以此类推，若 Ͳ ᦙ 䁞 Ͳ ᦙͲ 䁞 Ͳ ᦙ 䁞 䁞 Ͳ ᦙ ͲͲ ．（ 为正整数），则 的值为 ________． 三、计算或解答题（本大题共 10 小题，共 90 分，解答应写出必要的文字说明、证明 过程或演算步骤） 16.计算： Ͳ sin t Ͳt 䁞 Ͳ Ͳ ͲͲ ． 17.先化简， Ͳ 䁞䁞 Ͳ Ͳ 䁞Ͳ Ͳ ，然后从 Ͳ Ͳ 范围内选取一个合适的整数 作为 的值代入求值． 18.如图，在 馰ԯ 中， 馰 ＝ ԯ ，点 댠 、 分别是线段 馰ԯ 、 댠 的中点，过点 作 馰ԯ 的平行线交 馰 的延长线于点 ，连接 ԯ ． （1）求证： 馰댠 ； （2）求证：四边形 댠ԯ 为矩形． 3 / 11 19.在数学实践与综合课上，某兴趣小组同学用航拍无人机对某居民小区的 、 Ͳ 号楼 进行测高实践，如图为实践时绘制的截面图．无人机从地面点 馰 垂直起飞到达点 处，测得 号楼顶部 的俯角为 ，测得 Ͳ 号楼顶部 的俯角为 ，此时航拍无 人机的高度为 米，已知 号楼的高度为 Ͳ 米，且 ԯ 和 댠 分别垂直地面于点 ԯ和 댠 ，点 馰 为 ԯ댠 的中点，求 Ͳ 号楼的高度．（结果精确到 Ǥ ） （参考数据 sin Ǥ ，cos Ǥ ，tan Ǥ ，sin ǤͲ ， cos Ǥ ，tan ͲǤ ） 20.新学期开始时，某校九年级一班的同学为了增添教室绿色文化，打造温馨舒适的 学习环境，准备到一家植物种植基地购买 、 馰 两种花苗．据了解，购买 种花苗 盆， 馰 种花苗 . 盆，则需 Ͳ 元；购买 种花苗 盆， 馰 种花苗 盆，则需 元． （1）求 、 馰 两种花苗的单价分别是多少元？ （2）经九年级一班班委会商定，决定购买 、 馰 两种花苗共 Ͳ 盆进行搭配装扮教 室．种植基地销售人员为了支持本次活动，为该班同学提供以下优惠：购买几盆 馰 种 花苗， 馰 种花苗每盆就降价几元，请你为九年级一班的同学预算一下，本次购买至少 准备多少钱？最多准备多少钱？ 21.阅读以下材料，并解决相应问题： 小明在课外学习时遇到这样一个问题： 定义：如果二次函数 ＝ ᦙ Ͳ 䁞 䁡 䁞 （ ᦙ ， ᦙ 、 䁡 、 是常数）与 ＝ ᦙͲ Ͳ 䁞 䁡Ͳ 䁞 Ͳ （ ᦙͲ ， ᦙͲ 、 䁡Ͳ 、 Ͳ 是常数）满足 ᦙ 䁞 ᦙͲ ＝ ， 䁡 ＝ 䁡Ͳ ， 䁞 Ͳ ＝ ，则这 4 / 11 两个函数互为“旋转函数”．求函数 ＝ Ͳ Ͳ 䁞 的旋转函数，小明是这样思考 的，由函数 ＝ Ͳ Ͳ 䁞 可知， ᦙ ＝ Ͳ ， 䁡 ＝ ， ＝ ，根据 ᦙ 䁞 ᦙͲ ＝ ， 䁡 ＝ 䁡Ͳ ， 䁞 Ͳ ＝ ，求出 ᦙͲ ， 䁡Ͳ ， Ͳ 就能确定这个函数的旋转函数． 请思考小明的方法解决下面问题： （1）写出函数 ＝ Ͳ 䁞 的旋转函数． （2）若函数 ＝ . Ͳ 䁞 䁞 与 ＝ . Ͳ 互为旋转函数，求 䁞 ͲͲ 的值． （3）已知函数 ＝ Ͳ 䁞 的图象与 轴交于 、 馰 两点，与 轴交于点 ԯ ， 点 、 馰 、 ԯ 关于原点的对称点分别是 、 馰 、 ԯ ，试求证：经过点 、 馰 、 ԯ 的二 次函数与 ＝ Ͳ 䁞 互为“旋转函数”． 22.端午节是中国的传统节日．今年端午节前夕，遂宁市某食品厂抽样调查了河东某 居民区市民对 、 馰 、 ԯ 、 댠 四种不同口味粽子样品的喜爱情况，并将调查情况绘制成 如图两幅不完整统计图： （1）本次参加抽样调查的居民有________人． （2）喜欢 ԯ 种口味粽子的人数所占圆心角为________度．根据题中信息补全条形统 计图． （3）若该居民小区有 人，请你估计爱吃 댠 种粽子的有________人． （4）若有外型完全相同的 、 馰 、 ԯ 、 댠 棕子各一个，煮熟后，小李吃了两个，请用 列表或画树状图的方法求他第二个吃的粽子恰好是 种粽子的概率． 5 / 11 23.如图，在平面直角坐标系中，已知点 的坐标为 标Ͳ ，点 馰 的坐标为 标 ，连 结 馰 ，以 馰 为边在第一象限内作正方形 馰ԯ댠 ，直线 馰댠 交双曲线 于 댠 、 两点，连结 ԯ ，交 轴于点 ． （1）求双曲线 和直线 댠 的解析式． （2）求 댠ԯ 的面积． 24.如图，在 馰ԯ 中， ԯ馰 ＝ ， 댠 为 馰 边上的一点，以 댠 为直径的 交 馰ԯ 于点 ，交 ԯ 于点 ，过点 ԯ 作 ԯ 馰 交 馰 于点 ，交 于点 ，过点 的弦 交 馰 于点 （ 不是直径），点 为弦 的中点，连结 馰 ， 馰 恰好 为 的切线． （1）求证： 馰ԯ 是 的切线． （2）求证： 댠 ． （3）若 sin 馰ԯ . ， ԯ ＝ . ，求四边形 ԯ 的面积． 6 / 11 25.如图，抛物线 ＝ ᦙ Ͳ 䁞 䁡 䁞 ᦙ 的图象经过 标 ， 馰标 ， ԯ标 三点． （1）求抛物线的解析式． （2）抛物线的顶点 与对称轴 上的点 关于 轴对称，直线 交抛物线于点 댠 ， 直线 馰 交 댠 于点 ，若直线 馰 将 馰댠 的面积分为 ‸Ͳ 两部分，求点 的坐标． （3） 为抛物线上的一动点， 为对称轴上动点，抛物线上是否存在一点 ，使 、 댠 、 、 为顶点的四边形为平行四边形？若存在，求出点 的坐标；若不存在，请 说明理由． 7 / 11 参考答案与试题解析 2020 年四川省遂宁市中考数学试卷 一、选择题（本大题共 10 个小题，每小题 4 分，共 40 分，在每个小题给出的四个选 项中，只有一个符合题目要求．） 1.A 2.B 3.D 4.C 5.D 6.D 7.C 8.C 9.B 10.B 二、填空题（本大题共 5 个小题，每小题 4 分，共 20 分） 11. 12. 13. 14. ܿ 15. 三、计算或解答题（本大题共 10 小题，共 90 分，解答应写出必要的文字说明、证明 过程或演算步骤） 16.原式＝ Ͳ Ͳ Ͳ Ͳ Ͳ 䁞 ＝ Ͳ Ͳ Ͳ 䁞 䁞 Ͳ 䁞 ． 17.原式＝ 䁞ͲͲ 䁞ͲͲ 䁞 Ͳ • Ͳ 䁞Ͳ ＝ 䁞Ͳ Ͳ Ͳ Ͳ Ͳ 䁞Ͳ Ͳ 䁞 䁞 Ͳ Ͳ 䁞 Ͳ 䁞 Ͳ Ͳ Ͳ 䁞 Ͳ＝ ＝ 䁞 ， ∵ Ͳ ， ∴可取 ＝ ， 则原式＝ 䁞 ＝ Ͳ ． 18.∵ 馰ԯ ， ∴ ＝ 댠馰 ， ∵ 是线段 댠 的中点， ∴ ＝ 댠 ， ∵ ＝ 댠馰 ， ∴ 馰댠 ； ∵ 馰댠 ， ∴ ＝ 馰댠 ， ∵ 댠 是线段 馰ԯ 的中点， ∴ 馰댠 ＝ ԯ댠 ， ∴ ＝ ԯ댠 ， ∵ ԯ댠 ， ∴四边形 댠ԯ 是平行四边形， ∵ 馰 ＝ ԯ ， ∴ 댠 馰ԯ ， ∴ 댠ԯ ＝ ， ∴四边形 댠ԯ 为矩形． 19. Ͳ 号楼的高度约为 .Ǥ 米． 20.设 、 馰 两种花苗的单价分别是 元和 元，则 䁞 . Ͳ 䁞 ，解得 Ͳ ， 8 / 11 答： 、 馰 两种花苗的单价分别是 Ͳ 元和 元； 设购买 馰 花苗 盆，则购买 花苗为 Ͳ 盆，设总费用为 元， 由题意得： ＝ ͲͲ 䁞 ＝ Ͳ 䁞 䁞 Ͳ Ͳ ， ∵ ܿ ．故 有最大值，当 ＝ . 时， 的最小值为 Ͳ ，当 ＝ 时， 的最小值 为 Ͳ ， 故本次购买至少准备 Ͳ 元，最多准备 Ͳ 元． 21.由 ＝ Ͳ 䁞 函数可知， ᦙ ＝ ， 䁡 ＝ ， ＝ ， ∵ ᦙ 䁞 ᦙͲ ＝ ， 䁡 ＝ 䁡Ͳ ， 䁞 Ͳ ＝ ， ∴ ᦙͲ ＝ ， 䁡Ͳ ＝ ， Ͳ ＝ ， ∴函数 ＝ Ͳ 䁞 的“旋转函数”为 ＝ Ͳ ； ∵ ＝ . Ͳ 䁞 䁞 与 ＝ . Ͳ 互为“旋转函数”， ∴ ， 解得： Ͳ ， ∴ 䁞 ͲͲ ＝ Ͳ 䁞 ͲͲ ＝ ． 证明：当 ＝ 时， ＝ Ͳ 䁞 ）＝ ， ∴点 ԯ 的坐标为 标 ． 当 ＝ 时， Ͳ 䁞 ＝ ， 解得： ＝ ， Ͳ ＝ ， ∴点 的坐标为 标 ，点 馰 的坐标为 标 ． ∵点 ， 馰 ， ԯ 关于原点的对称点分别是 ， 馰 ， ԯ ， ∴ 标 ， 馰标 ， ԯ标 ． 设过点 ， 馰 ， ԯ 的二次函数解析式为 ＝ ᦙ 䁞 ， 将 ԯ标 代入 ＝ ᦙ 䁞 ，得： ＝ ᦙ ， 解得： ᦙ ＝ Ͳ ， 过点 ， 馰 ， ԯ 的二次函数解析式为 ＝ Ͳ 䁞 ，即 ＝ Ͳ Ͳ 䁞 䁞 ． ∵ ＝ Ͳ 䁞 ＝ Ͳ Ͳ 䁞 ， ∴ ᦙ ＝ Ͳ ， 䁡 ＝ ， ＝ ， ᦙͲ ＝ Ͳ ， 䁡Ͳ ＝ ， Ͳ ＝ ， ∴ ᦙ 䁞 ᦙͲ ＝ Ͳ 䁞 Ͳ ＝ ， 䁡 ＝ 䁡Ͳ ＝ ， 䁞 Ͳ ＝ 䁞 ＝ ， ∴经过点 ， 馰 ， ԯ 的二次函数与函数 ＝ Ͳ 䁞 互为“旋转函数”． 22. Ͳ Ͳ画树状图为： 共有 Ͳ 种等可能的结果数，其中他第二个吃的粽子恰好是 种粽子的结果数为 ， 所以他第二个吃的粽子恰好是 种粽子的概率 Ͳ ． 23.，点 馰 的坐标为 标 ， ∴ ＝ Ͳ ， 馰 ＝ ， 作 댠 轴于 ， ∵四边形 馰ԯ댠 是正方形， ∴ 馰댠 ＝ ， 馰 ＝ 댠 ， ∴ 馰 䁞 댠 ＝ ， ∵ 馰 䁞 馰 ＝ ， ∴ 댠 ＝ 馰 ， 在 馰 和 댠 中 馰 댠 馰 댠 馰 댠 ， ∴ 馰 댠 ， 9 / 11 ∴ ＝ 馰 ＝ ， 댠 ＝ ＝ Ͳ ， ∴ 댠Ͳ ， ， ∵双曲线 经过 댠 点， ∴ ＝ Ͳ ＝ ， ∴双曲线为 ， 设直线 댠 的解析式为 ＝ 䁞 ， 把 馰标 ， 댠Ͳ ,（1）代入得 䁞 Ͳ 䁞 ，解得 ， ∴直线 댠 的解析式为 ＝ ； Ͳ 连接 ԯ ，交 馰댠 于 ， ∵四边形 馰ԯ댠 是正方形， ∴ 馰댠 垂直平分 ԯ ， ԯ ＝ 馰댠 ， 解 得 Ͳ 或 ， ∴ 标 ， ∵ 馰标 ， 댠Ͳ ,（4）， ∴ 댠 Ͳ 䁞 Ͳ 䁞 䁞 Ͳ ， 댠馰 Ͳ Ͳ 䁞 Ͳ ， ∴ ԯ Ͳ 馰댠 Ͳ ， ∴ 댠ԯ Ͳ 댠 ԯ Ͳ Ͳ . Ͳ ． 24.证明：连接 ， ， ∵ 馰 ，点 为弦 的中点， ∴ 馰 垂直平分 ， ∴ 馰 ＝ 馰 ， ∵ ＝ ， 馰 ＝ 馰 ， ∴ 馰 馰 ， ∴ 馰 ＝ 馰 ， ∵ 馰 为 的切线， ∴ 馰 ＝ ， ∴ 馰 ＝ ， ∴ 馰ԯ ， ∴ 馰ԯ 是 的切线． ∵ 馰 ＝ ԯ馰 ＝ ， ∴ ԯ ， ∴ ԯ ＝ ， ∵ ＝ ， ∴ ＝ ， ∴ ԯ ＝ ， ∴ 댠 ． ∵ 댠 为的 直径，点 为弦 的中点， 10 / 11 ∴ 馰 ， ∵ ԯ 馰 ， ∴ ԯ ， ∵ ԯ馰 ＝ 馰 ＝ ， ∴ ԯ ， ∴ ԯ ＝ ， ∵ ＝ ， ∴ ＝ ， ∴ ԯ ＝ ， ∵ ԯ ＝ ＝ ， ＝ ， ∴ ԯ ， ∴ ԯ ＝ ， ∵ ԯ 䁞 ԯ ＝ 䁞 ＝ ， ∴ ԯ ＝ ， ∵ ＝ ԯ ， ∴ ԯ ＝ ԯ ， ∴ ԯ ＝ ԯ ， ∴ ԯ ＝ ， ∴四边形 ԯ 是平行四边形， ∵ ԯ ＝ ԯ ， ∴四边形 ԯ 是菱形， ∵sin 馰ԯ sin ԯ ԯ . ， ∵ ԯ ＝ . ， ∴ ＝ ， ∴ ԯ ԯ Ͳ Ͳ Ͳ ， ∵ ԯ ， ∴ ＝ ԯ ＝ . ， ∴ ＝ ， ∵ Ͳ ＝ Ͳ 䁞 Ͳ ， ∴ Ͳ ＝ Ͳ Ͳ 䁞 Ͳ ， 解得： . Ͳ ， ∴ ԯ ＝ . Ͳ ， ∴四边形 ԯ 的面积＝ ԯ . Ͳ ＝ . ． 25.∵抛物线 ＝ ᦙ Ͳ 䁞 䁡 䁞 ᦙ 的图象经过 标 ， 馰标 ， ∴设抛物线解析式为： ＝ ᦙ ， ∵抛物线 ＝ ᦙ ᦙ 的图象经过点 ԯ标 ， ∴ ＝ ᦙ ， ∴ ᦙ ＝ Ͳ ， ∴抛物线解析式为： ＝ Ͳ ＝ Ͳ Ͳ 䁞 ； ∵ ＝ Ͳ Ͳ 䁞 ＝ Ͳ Ͳ Ͳ Ͳ ， ∴顶点 的坐标为 Ͳ标 Ͳ ， ∵抛物线的顶点 与对称轴 上的点 关于 轴对称， ∴点 Ͳ标Ͳ ， 设直线 解析式为： ＝ 䁞 䁡 ， 由题意可得： 䁞 䁡 Ͳ Ͳ 䁞 䁡 ， 11 / 11 解得： Ͳ 䁡 Ͳ ， ∴直线 解析式为： ＝ Ͳ Ͳ ， 联立方程组得： Ͳ Ͳ Ͳ Ͳ 䁞 ， 解得： ， Ͳ Ͳ ， ∴点 댠标 ， ∴ 馰댠 Ͳ Ͳ ＝ ， 设点 标Ͳ Ͳ ， ∵直线 馰 将 馰댠 的面积分为 ‸Ͳ 两部分， ∴ 馰 馰댠 ＝ Ͳ 或 馰 Ͳ 馰댠 ＝ ， ∴ Ͳ Ͳ Ͳ Ͳ ＝ Ͳ 或 Ͳ Ͳ Ͳ Ͳ ＝ ， ∴ ＝ Ͳ 或 ， ∴点 Ͳ标Ͳ 或 标 ； 若 댠 为平行四边形的边， ∵以 、 댠 、 、 为顶点的四边形为平行四边形， ∴ 댠 ＝ ， ∴ 댠 ＝ 或 댠 ＝ ， ∴ ＝ 䁞 Ͳ ＝ . 或 ＝ Ͳ 䁞 ＝ ， ∴点 坐标为 .标 或 标 ； 若 댠 为平行四边形的对角线， ∵以 、 댠 、 、 为顶点的四边形为平行四边形， ∴ 댠 与 互相平分， ∴ 䁞 댠 Ͳ 䁞 Ͳ ， ∴ ＝ ， ∴点 坐标为 标 ， 综上所述：当点 坐标为 .标 或 标 或 标 时，使 、 댠 、 、 为顶点的四 边形为平行四边形．