中考数学专题复习练习：全等三角形判定（二） 13页

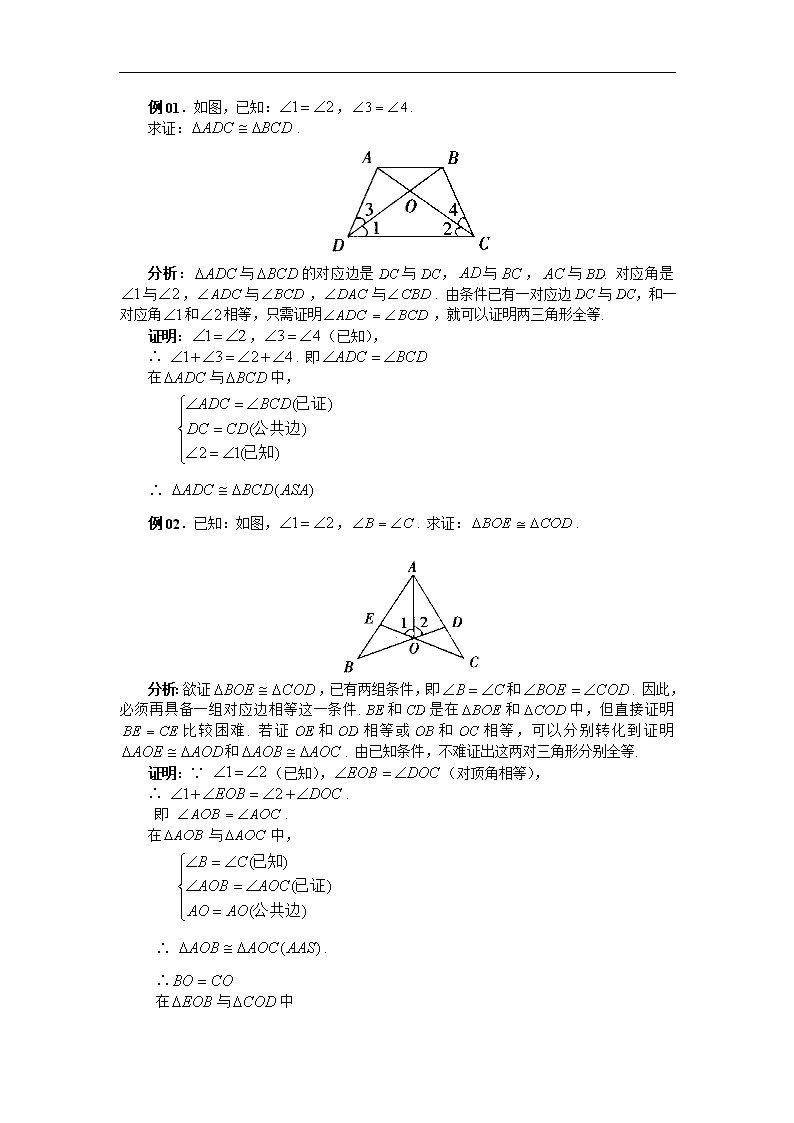
例01．如图，已知：，. ‎ 求证：. ‎ 分析：与的对应边是DC与DC，与，与BD. 对应角是与，与，与. 由条件已有一对应边DC与DC，和一对应角和相等，只需证明，就可以证明两三角形全等. ‎ 证明：，（已知），‎ ‎∴ . 即 在与中，‎ ‎∴ ‎ 例02．已知：如图，，. 求证：. ‎ 分析：欲证，已有两组条件，即和. 因此，必须再具备一组对应边相等这一条件. BE和CD是在和中，但直接证明比较困难. 若证OE和OD相等或OB和OC相等，可以分别转化到证明和. 由已知条件，不难证出这两对三角形分别全等. ‎ 证明：∵ （已知），（对顶角相等），‎ ‎∴ .‎ ‎ 即 . ‎ 在与中，‎ ‎∴ . ‎ ‎∴‎ 在与中 ‎ ‎ ‎∴ （ASA）‎ 例03．如图，已知：AB与CD相交于点O，且，E、F为AB上两点，且. ‎ 求证：. ‎ 分析：欲证，已具备了两个条件，和. 所以只需证另一对角相等或证明，即可. 证明另一对角相等，比较困难. 所以就证明. 因为有. 要证只需证即可. 由已知条件容易证得，从而证明. ‎ 证明：∵（已知）‎ ‎∴（两直线平行，内错角相等）‎ 在与中，‎ ‎∴ ‎ ‎∴（全等三角形的对应边相等）‎ ‎∵（已知），‎ ‎∴. ‎ 即 在与中，‎ ‎∴‎ 例04．如图，已知：. ‎ 求证：. ‎ 分析：欲证相等的两条线段AD，AE分别在和中，由于，，所以只需再证即可，这由已知条件容易得到. ‎ 证明：∵（已知）‎ ‎∴‎ 即 在与中，‎ ‎∴‎ ‎∴（全等三角形的对应边相等）‎ 例05．已知：（如图）. ‎ 求证：‎ 分析：要证，只要证即可，在和中，已知，，只要再证一边对应相等即可，根据已知可得 ‎，从而可证，进而可证，思路即为：“AAS”‎ 证明：在和中 ‎∴‎ ‎∴（全等三角形的对应边相等）‎ 在和中 ‎∴ ‎ ‎∴ （全等三角形的对应边相等）‎ 例06．求证：三角形的一边的两端到这边的中线或中线的延长线的距离相等. ‎ 分析：这是一道了题，必须先根据题意画出图形，再结合题意写出已知，求证，再证明. ‎ 已知：AD是的中线. 如图，且于F，的延长线于E，‎ 求证：‎ 证明：∵AD为的中线（已知）‎ ‎∴ （中线定义）‎ ‎∵ （已知）‎ ‎∴ （等于定义）‎ 在与中 ‎∴（AAS）‎ ‎∴（全等三角形对应边相等）‎ 说明 本题还可利用面积相等来证明，提示，过A作于N，希同学们自己来证明. ‎ 例07．已知：如图，，‎ 求证：. ‎ 分析：因为四边形，我只学过三角形的有关知识，因此只要连结四边形的对角线从而把四边形的总是转化为三角形的总是来解决. ‎ 证明：连结AC ‎∵（已知）‎ ‎∴（两直线平行内错角相等）‎ 在和中 ‎∴ ‎ ‎∴（全等三角形的对应边相等）‎ 例08．已知：如图，‎ 求证：‎ 证明：在和中 ‎∴ ‎ ‎∴ （全等三角形的对应角相等）‎ 在和中 ‎∴‎ ‎∴（全等三角形的对应边相等）‎ ‎ 说明 找到题目中的隐性条件并加以应用是关键.‎ 例09．如图，在和中，，P是BC上任意一点，‎ 求证：. ‎ 证明：在和中，‎ ‎∴ ‎ ‎∴ （全等三角形对应边相等）‎ 在和中，‎ ‎∴ ‎ ‎∴ （全等三角形对应边相等）‎ 说明：本题也可通过，得到，从而证，得到. ‎ 选择题 ‎（1）已知与，，，..那么下列结论正确的是（ ）‎ ‎（A） （B）‎ ‎（C） （D）以上答案都不对 ‎（2）在和，甲：；乙：；丙：；丁：；戊：；己：，则不能保证≌成立的条件为（ ）‎ ‎（A）丙、丁、己 （B）甲、丙、戊 ‎（C）甲、乙、戊 （D）乙、戊、己 ‎（3）如图，已知和均为等边三角形，那么≌的根据是（ ）‎ ‎（A）ASA （B）SAS ‎ ‎（C）AAS （D）以上都不对 ‎（4）如图，C是BE上一点，，，，那么（ ）‎ ‎（A）‎ ‎（B）C是BE的中点 ‎（C）‎ ‎（D）以上结论都正确 参考答案：‎ ‎（1）C （2）B （3）B （4）D 填空题 ‎（1）如图，已知：，.‎ 求证：.‎ 证明：在与中，‎ ‎∴≌（ ）‎ ‎∴‎ ‎（2）如图，已知：，，垂足分别为B，D..‎ 求证：.‎ 证明：在与中，‎ ‎∴ ≌（ ）‎ ‎∴（ ）‎ ‎（3）如图，已知：，.求证：≌.‎ 证明：在与中，‎ ‎∴ ≌（ASA）‎ ‎（4）如图，已知：，.求证：≌.‎ 证明：在与中，‎ ‎ ∴≌（ ）‎ 参考答案：‎ ‎（1）AB；公共边；AAS；全等三角形的对应边相等 ‎ ‎（2）垂直定义；已知；公共边；AAS；全等三角形的对应边相等.‎ ‎（3）已知：；；对顶角相等 ‎ ‎（4）公共角；已知；AAS ‎ 证明题 ‎1．如图，已知，，.‎ 求证：.‎ ‎2．如图，已知：，.‎ 求证：点B是线段AC的中点.‎ ‎3．如图，已知：，.‎ 求证：.‎ ‎4．如图，已知：在中，AD是的平分线，于E，于C，求证：.‎ ‎5．如图，已知：E在AC上，，.‎ 求证：.‎ ‎6．如图，已知：，，，直线DC过E点交AD于D，交BC于C.‎ 求证：.‎ ‎7．求证：三角形一边的两个端点到这边上的中线的距离相等.‎ ‎8．如图，已知：，直线AE，BD相交于点C，，，交BD于F.‎ 求证：.‎ ‎9．如图，已知：AB与CD相交于点O，O是AB，CD的中点，过点O引直线EF分别与AD，BC相交于E、F两点.‎ 求证：.‎ 参考答案：‎ ‎1．证：由，，可得.易证≌，∴ ‎ ‎2．证：易证≌，∴ ，由此可证：.因此，可证≌.∴，∴B是AC的中点.‎ ‎3．易证≌，∴，，又∵，∴.由此可证≌，∴‎ ‎4．，，，∴，∴.‎ ‎5．∵ ，，，∴≌，∴，又∵,，∴，∴‎ ‎6．在AB上取一点F，使，又∵，，∴，∴，又∵，由此可推出.可证，∴，∴.‎ ‎7．已知：如图，AD为的中线，于F，于E.‎ 求证：.‎ 证：，，，‎ ‎∴ ,‎ ‎∴ ‎ ‎8．证：∵ ， ∴，‎ 又∵，，‎ ‎∴ ‎ ‎∴ ，∴ 可证，∴‎ ‎9．证：，，，∴，∴.而，，∴，∴ ‎ 能力：1、如图1，已知：AD平分∠BAC，AB=AC，连接BD，CD，并延长相交AC、AB于F、E点.‎ 则图形中有（ ）对全等三角形.‎ A B B、4对 ‎ E F D C A D B O C ‎1‎ ‎2‎ A、2 B、3 C、4 D、5‎ 图2‎ 图1‎ 答案：C.‎ ‎2、如图2，已知：∠1=∠2，AB=DC，图中全等三角形的对数是（ ）‎ A、0 B、1 C、2 D、3‎ 答案：A A F C D B E ‎3、如图3，已知：△ABC中，DF=FE，BD=CE，AF⊥BC于F，则此图中全等三角形共有（ ）‎ A A、5对 B、4对 C、3对 D2对 图3‎ A B D F E C ‎ ‎ 图4‎ 答案：C.‎ ‎1、如图4，已知：在△ABC中，AD是BC边上的高，AD=BD，DE=DC，延长BE交AC于F，‎ 求证：BF是△ABC中边上的高.‎ 提示：关键证明△ADC≌△BFC ‎2、如图5，已知：∠D=∠E，DN=EM，AM=CN，求证：点B是线段AC的中点.‎ 提示：欲证点B是线段AC的中点，只需证AB＝BC.选择AB、BC所在的两个三角形，然后证这两个三角形△AMB≌△CNB.由条件可得△EMB≌△DNB，所以得到∠EMB＝∠DNB，MB＝NB A D B C A M N E C D B 由此易证△AMB≌△CNB.‎ O 图6‎ 图5‎ ‎3、如图6，已知：AB=CD，∠A=∠D.求证：∠ABC=∠DCB 提示：欲证∠ABC=∠DCB，选择这两个角所在的三角形，只需证△ABC≌△DBC 由条件可知△ADC≌△DAB，所以得到∠DAC＝∠ADB，BD＝AC，加之条件利用边角边公理可证 ‎△ABC≌△DBC ‎4、如图7，已知：在△ABC中，∠ACB=,AC=BC，AE是BC边上的中线过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于点D.‎ ‎（1）求证：AE=CD.‎ ‎（2）AC=12cm，求BD的长.‎ 提示：欲证AE=CD，只需证△ACE≌△CBD由条件可知∠CAE＝∠BCD（同角的余角相等）加之其它两个条件易证得结论.‎ 由E是BC的中点，EC＝BE又BD＝EC，BC＝AC知BD＝6 cm E ‎┛‎ ‎┓‎ ‎┏‎ D B A C F 图7‎ B A E C D 图8‎ F ‎5、如图8，已知：在△ABC中，AB=AC，∠A=90，BD平分∠ABC交AC于D，CE⊥BD交BD的延长线于E，求证：BD=2CE 提示：本题的关键是从结论BD=2CE出发，想到构造线段CF＝2CE，再证BD＝CF ‎　　　　　　　‎