- 859.00 KB
- 2021-11-12 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2017年辽宁省营口市中考数学试卷
一、选择题(下列各题的备选答案中,只有一个正确的,每小题3分,共30分.)
1.(3分)﹣5的相反数是( )
A.﹣5 B.±5 C. D.5
2.(3分)下列几何体中,同一个几何体的三视图完全相同的是( )
A.球 B.圆锥 C.圆柱 D.三棱柱
3.(3分)下列计算正确的是( )
A.(﹣2xy)2=﹣4x2y2 B.x6÷x3=x2 C.(x﹣y)2=x2﹣y2 D.2x+3x=5x
4.(3分)为了解居民用水情况,小明在某小区随机抽查了30户家庭的月用水量,结果如下表:
月用水量/m3
4
5
6
8
9
10
户数
6
7
9
5
2
1
则这30户家庭的月用水量的众数和中位数分别是( )
A.6,6 B.9,6 C.9,6 D.6,7
5.(3分)若一次函数y=ax+b的图象经过第一、二、四象限,则下列不等式一定成立的是( )
A.a+b<0 B.a﹣b>0 C.ab>0 D.<0
6.(3分)如图,已知矩形纸片的一条边经过一个含30°角的直角三角尺的直角顶点,若矩形纸片的一组对边分别与直角三角尺的两边相交,∠2=115°,则∠1的度数是( )
A.75° B.85° C.60° D.65°
7.(3分)如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )
A.∠ECD=112.5° B.DE平分∠FDC C.∠DEC=30° D.AB=CD
8.(3分)如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y=的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
A.y=﹣ B.y=﹣ C.y=﹣ D.y=
9.(3分)如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
A.4 B.5 C.6 D.7
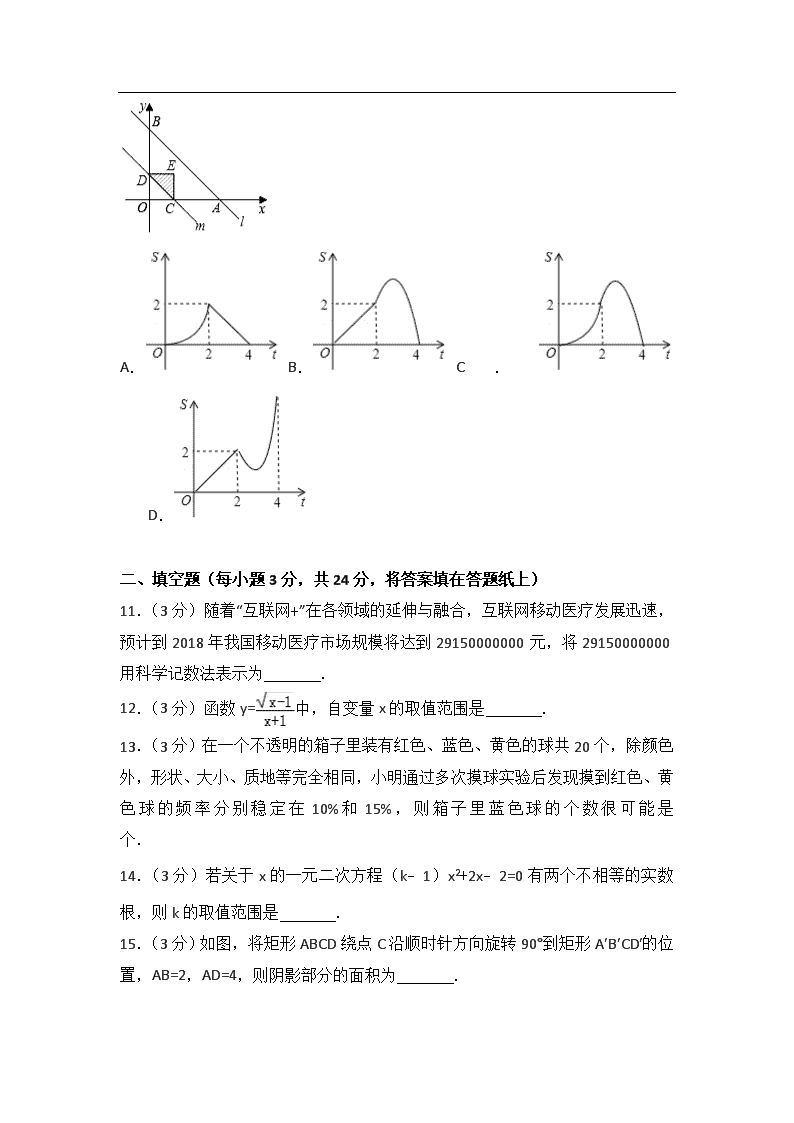
10.(3分)如图,直线l的解析式为y=﹣x+4,它与x轴和y轴分别相交于A,B两点.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动.它与x轴和y轴分别相交于C,D两点,运动时间为t秒(0≤t≤4),以CD为斜边作等腰直角三角形CDE(E,O两点分别在CD两侧).若△CDE和△OAB的重合部分的面积为S,则S与t之间的函数关系的图象大致是( )
A. B. C. D.
二、填空题(每小题3分,共24分,将答案填在答题纸上)
11.(3分)随着“互联网+”在各领域的延伸与融合,互联网移动医疗发展迅速,预计到2018年我国移动医疗市场规模将达到29150000000元,将29150000000用科学记数法表示为 .
12.(3分)函数y=中,自变量x的取值范围是 .
13.(3分)在一个不透明的箱子里装有红色、蓝色、黄色的球共20个,除颜色外,形状、大小、质地等完全相同,小明通过多次摸球实验后发现摸到红色、黄色球的频率分别稳定在10%和15%,则箱子里蓝色球的个数很可能是 个.
14.(3分)若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有两个不相等的实数根,则k的取值范围是 .
15.(3分)如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为 .
16.(3分)某市为绿化环境计划植树2400棵,实际劳动中每天植树的数量比原计划多20%,结果提前8天完成任务.若设原计划每天植树x棵,则根据题意可列方程为 .
17.(3分)在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
18.(3分)如图,点A1(1,)在直线l1:y=x上,过点A1作A1B1⊥l1交直线l2:y=x于点B1,A1B1为边在△OA1B1外侧作等边三角形A1B1C1,再过点C1作A2B2⊥l1,分别交直线l1和l2于A2,B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2,…按此规律进行下去,则第n个等边三角形AnBnCn的面积为 .(用含n的代数式表示)
三、解答题(19小题10分,20小题10分,共20分.)
19.(10分)先化简,再求值:(﹣)÷(1﹣),其中x=()﹣1﹣(2017﹣)0,y=sin60°.
20.(10分)如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A、B、C、D表示).
四、解答题(21题12分,22小题12分,共24分)
21.(12分)某中学开展“汉字听写大赛”活动,为了解学生的参与情况,在该校随机抽取了四个班级学生进行调查,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,解答下列问题:
(1)这四个班参与大赛的学生共 人;
(2)请你补全两幅统计图;
(3)求图1中甲班所对应的扇形圆心角的度数;
(4)若四个班级的学生总数是160人,全校共2000人,请你估计全校的学生中参与这次活动的大约有多少人.
22.(12分)如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点A处测得码头C在船的东北方向,航行40分钟后到达B处,这时码头C恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头C的最近距离.(结果精确到0.1海里,参考数据≈1.41,≈1.73)
五、解答题(23小题12分,24小题12分,共24分)
23.(12分)如图,点E在以AB为直径的⊙O上,点C是的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.
(1)求证:CD是⊙O的切线;
(2)若cos∠CAD=,BF=15,求AC的长.
24.(12分)夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第x天生产空调y台,直接写出y与x之间的函数解析式,并写出自变量x的取值范围.
(2)若每台空调的成本价(日生产量不超过50台时)为2000元,订购价格为每台2920元,设第x天的利润为W元,试求W与x之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.
六、解答题(本题满分14分)
25.(14分)在四边形中ABCD,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)若四边形ABCD为正方形.
①如图1,请直接写出AE与DF的数量关系 ;
②将△EBF绕点B逆时针旋转到图2所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由;
(3)如图3,若四边形ABCD为矩形,BC=mAB,其它条件都不变,将△EBF绕点B顺时针旋转α(0°<α<90°)得到△E'BF',连接AE',DF',请在图3中画出草图,并直接写出AE'与DF'的数量关系.
七、解答题(本题满分14分)
26.(14分)如图,抛物线y=ax2+bx﹣2的对称轴是直线x=1,与x轴交于A,B两点,与y轴交于点C,点A的坐标为(﹣2,0),点P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E.
(1)求抛物线解析式;
(2)若点P在第一象限内,当OD=4PE时,求四边形POBE的面积;
(3)在(2)的条件下,若点M为直线BC上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点B,D,M,N为顶点的四边形是菱形?若存在上,直接写出点N的坐标;若不存在,请说明理由.
【温馨提示:考生可以根据题意,在备用图中补充图形,以便探究】
2017年辽宁省营口市中考数学试卷
参考答案与试题解析
一、选择题(下列各题的备选答案中,只有一个正确的,每小题3分,共30分.)
1.(3分)(2017•营口)﹣5的相反数是( )
A.﹣5 B.±5 C. D.5
【分析】根据相反数的定义直接求得结果.
【解答】解:﹣5的相反数是5.
故选:D.
【点评】本题主要考查了相反数的性质,只有符号不同的两个数互为相反数,0的相反数是0.
2.(3分)(2017•营口)下列几何体中,同一个几何体的三视图完全相同的是( )
A.球 B.圆锥 C.圆柱 D.三棱柱
【分析】分别写出各个立体图形的三视图,判断即可.
【解答】解:A、球体的主视图、左视图、俯视图都是圆形;故本选项正确
B、圆锥的主视图、左视图都是三角形,俯视图是圆形;故本选项错误;
C、圆柱的主视图、左视图是矩形、俯视图是圆,故本选项错误;
D、三棱柱球体的主视图、左视图是三角形、俯视图三角形,但大小不一定相同,故本选项正确.
故选:A.
【点评】本题考查了简单几何体的三视图,掌握主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形是解题的关键.
3.(3分)(2017•营口)下列计算正确的是( )
A.(﹣2xy)2=﹣4x2y2 B.x6÷x3=x2 C.(x﹣y)2=x2﹣y2 D.2x+3x=5x
【分析】根据同底数幂的除法、积的乘方、完全平方公式和合并同类项的运算法则分别进行计算即可得出答案.
【解答】解:A、(﹣2xy)2=4x2y2,故本选项错误;
B、x6÷x3=x3,故本选项错误;
C、(x﹣y)2=x2﹣2xy+y2,故本选项错误;
D、2x+3x=5x,故本选项正确;
故选D.
【点评】此题考查了同底数幂的除法、积的乘方、完全平方公式和合并同类项,熟练掌握运算法则是解题的关键,是一道基础题.
4.(3分)(2017•营口)为了解居民用水情况,小明在某小区随机抽查了30户家庭的月用水量,结果如下表:
月用水量/m3
4
5
6
8
9
10
户数
6
7
9
5
2
1
则这30户家庭的月用水量的众数和中位数分别是( )
A.6,6 B.9,6 C.9,6 D.6,7
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
【解答】解:表中数据为从小到大排列,数据6出现了9次最多为众数,
在第15位、第16位都是6,其平均数6为中位数,所以本题这组数据的中位数是6,众数是6.
故选A.
【点评】本题主要考查了众数和中位数的知识,一组数据中出现次数最多的数据叫做众数,将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.
5.(3分)(2017•营口)若一次函数y=ax+b的图象经过第一、二、四象限,则下列不等式一定成立的是( )
A.a+b<0 B.a﹣b>0 C.ab>0 D.<0
【分析】由于一次函数y=ax+b的图象经过第一、二、四象限,由此可以确定a<0,b>0,然后一一判断各选项即可解决问题.
【解答】解:∵一次函数y=ax+b的图象经过第一、二、四象限,
∴a<0,b>0,
∴a+b不一定大于0,故A错误,
a﹣b<0,故B错误,
ab<0,故C错误,
<0,故D正确.
故选D.
【点评】本题考查一次函数的图象与系数的关系,解题的关键是学会根据函数图象的位置,确定a、b的符号,属于中考常考题型.
6.(3分)(2017•营口)如图,已知矩形纸片的一条边经过一个含30°角的直角三角尺的直角顶点,若矩形纸片的一组对边分别与直角三角尺的两边相交,∠2=115°,则∠1的度数是( )
A.75° B.85° C.60° D.65°
【分析】先根据平行线的性质,得出∠3的度数,再根据三角形外角性质进行计算即可.
【解答】解:如图所示,∵DE∥BC,
∴∠2=∠3=115°,
又∵∠3是△ABC的外角,
∴∠1=∠3﹣∠A=115°﹣30°=85°,
故选:B.
【点评】本题主要考查了平行线的性质以及三角形外角性质的运用,解题时注意:两直线平行,同位角相等.
7.(3分)(2017•营口)如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )
A.∠ECD=112.5° B.DE平分∠FDC C.∠DEC=30° D.AB=CD
【分析】由AB=AC,∠CAB=45°,根据等边对等角及三角形内角和定理求出∠B=∠ACB=67.5°.由Rt△ADC中,∠CAD=45°,∠ADC=90°,根据三角形内角和定理求出∠ACD=45°,根据等角对等边得出AD=DC,那么∠ECD=∠ACB+∠ACD=112.5°,从而判断A正确;
根据三角形的中位线定理得到FE=AB,FE∥AB,根据平行线的性质得出∠EFC=∠BAC=45°,∠FEC=∠B=67.5°.根据直角三角形的性质以及等腰三角形的性质得到FD=AC,DF⊥AC,∠FDC=45°,等量代换得到FE=FD,再求出∠FDE=∠FED=22.5°,进而判断B正确;
由∠FEC=∠B=67.5°,∠FED=22.5°,求出∠DEC=∠FEC﹣∠FED=45°,从而判断C错误;
在等腰Rt△ADC中利用勾股定理求出AC=CD,又AB=AC,等量代换得到AB=CD,从而判断D正确.
【解答】解:∵AB=AC,∠CAB=45°,
∴∠B=∠ACB=67.5°.
∵Rt△ADC中,∠CAD=45°,∠ADC=90°,
∴∠ACD=45°,AD=DC,
∴∠ECD=∠ACB+∠ACD=112.5°,故A正确,不符合题意;
∵E、F分别是BC、AC的中点,
∴FE=AB,FE∥AB,
∴∠EFC=∠BAC=45°,∠FEC=∠B=67.5°.
∵F是AC的中点,∠ADC=90°,AD=DC,
∴FD=AC,DF⊥AC,∠FDC=45°,
∵AB=AC,
∴FE=FD,
∴∠FDE=∠FED=(180°﹣∠EFD)=(180°﹣135°)=22.5°,
∴∠FDE=∠FDC,
∴DE平分∠FDC,故B正确,不符合题意;
∵∠FEC=∠B=67.5°,∠FED=22.5°,
∴∠DEC=∠FEC﹣∠FED=45°,故C错误,符合题意;
∵Rt△ADC中,∠ADC=90°,AD=DC,
∴AC=CD,
∵AB=AC,
∴AB=CD,故D正确,不符合题意.
故选C.
【点评】本题考查的是三角形中位线定理,等腰三角形的判定与性质,直角三角形的性质,平行线的性质,勾股定理等知识.掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
8.(3分)(2017•营口)如图,在菱形ABOC中,∠
A=60°,它的一个顶点C在反比例函数y=的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
[来源:学科网]
A.y=﹣ B.y=﹣ C.y=﹣ D.y=
【分析】过点C作CD⊥x轴于D,设菱形的边长为a,根据菱形的性质和三角函数分别表示出C,以及点A向下平移2个单位的点,再根据反比例函数图象上点的坐标特征得到方程组求解即可.
【解答】解:过点C作CD⊥x轴于D,
设菱形的边长为a,
在Rt△CDO中,OD=a•cos60°=a,CD=a•sin60°=a,
则C(﹣a,a),
点A向下平移2个单位的点为(﹣a﹣a,a﹣2),即(﹣a,a﹣2),
则,
解得.
故反比例函数解析式为y=﹣.
故选:A.
【点评】本题考查的是反比例函数综合题目,考查了反比例函数解析式的求法、坐标与图形性质、菱形的性质、平移的性质等知识;本题综合性强,有一定难度.
9.(3分)(2017•营口)如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
A.4 B.5 C.6 D.7
【分析】过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP,此时DP+CP=DP+PC′=DC′的值最小.由DC=1,BC=4,得到BD=3,连接BC′,由对称性可知∠C′BA=∠CBA=45°,于是得到∠CBC′=90°,然后根据勾股定理即可得到结论.
【解答】解:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP.
此时DP+CP=DP+PC′=DC′的值最小.
∵BD=3,DC=1
∴BC=4,
∴BD=3,
连接BC′,由对称性可知∠C′BA=∠CBA=45°,
∴∠CBC′=90°,
∴BC′⊥BC,∠BCC′=∠BC′C=45°,
∴BC=BC′=4,
根据勾股定理可得DC′===5.
故选B.
【点评】此题考查了轴对称﹣线路最短的问题,确定动点P何位置时,使PC+PD的值最小是解题的关键.
10.(3分)(2017•营口)如图,直线l的解析式为y=﹣x+4,它与x轴和y轴分别相交于A,B两点.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动.它与x轴和y轴分别相交于C,D两点,运动时间为t秒(0≤t≤4),以CD为斜边作等腰直角三角形CDE(E,O两点分别在CD两侧).若△CDE和△OAB的重合部分的面积为S,则S与t之间的函数关系的图象大致是( )
A. B. C.
D.
【分析】分别求出0<t≤2和2<t≤4时,S与t的函数关系式即可爬判断.
【解答】解:当0<t≤2时,S=t2,
当2<t≤4时,S=t2﹣(2t﹣4)2=﹣t2+8t﹣8,
观察图象可知,S与t之间的函数关系的图象大致是C.
故答案为C.
【点评】本题考查动点问题的函数图象,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.
二、填空题(每小题3分,共24分,将答案填在答题纸上)
11.(3分)(2017•营口)随着“互联网+”在各领域的延伸与融合,互联网移动医疗发展迅速,预计到2018年我国移动医疗市场规模将达到29150000000元,将29150000000用科学记数法表示为 2.915×1010 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.
【解答】解:29150000000=2.915×1010.
故答案为:2.915×1010.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
12.(3分)(2017•营口)函数y=中,自变量x的取值范围是 x≥1 .
【分析】根据二次根式的性质和分式的意义,被开方数大于等于0,可知:x﹣1
≥0;分母不等于0,可知:x+1≠0,所以自变量x的取值范围就可以求出.
【解答】解:根据题意得:x,﹣1≥0且x+1≠0,
解得:x≥1.
故答案为:x≥1.
【点评】考查使得分式和二次根式有意义的知识.函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.
13.(3分)(2017•营口)在一个不透明的箱子里装有红色、蓝色、黄色的球共20个,除颜色外,形状、大小、质地等完全相同,小明通过多次摸球实验后发现摸到红色、黄色球的频率分别稳定在10%和15%,则箱子里蓝色球的个数很可能是 15 个.
【分析】利用频率估计概率,可得到摸到红色、黄色球的概率为10%和15%,则摸到蓝球的概率为75%,然后根据概率公式可计算出口袋中蓝色球的个数.
【解答】解:根据题意得摸到红色、黄色球的概率为10%和15%,
所以摸到蓝球的概率为75%,
因为20×75%=15(个),
所以可估计袋中蓝色球的个数为15个.
故答案为15.
【点评】本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
14.(3分)(2017•营口)若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有两个不相等的实数根,则k的取值范围是 k>且k≠1 .
【分析】根据一元二次方程的定义和判别式的意义得到k﹣1≠0且△=22﹣4(k﹣1)×(﹣2)>0,然后求出两个不等式的公共部分即可.
【解答】解:根据题意得k﹣1≠0且△=22﹣4(k﹣1)×(﹣2)>0,
解得:k>且k≠1.
故答案为:k>且k≠1.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.
15.(3分)(2017•营口)如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为 π﹣2 .
【分析】先求出CE=2CD,求出∠DEC=30°,求出∠DCE=60°,DE=2,分别求出扇形CEB′和三角形CDE的面积,即可求出答案.
【解答】解:∵四边形ABCD是矩形,
∴AD=BC=4,CD=AB=2,∠BCD=∠ADC=90°,
∴CE=BC=4,
∴CE=2CD,
∴∠DEC=30°,
∴∠DCE=60°,
由勾股定理得:DE=2,
∴阴影部分的面积是S=S扇形CEB′﹣S△CDE=﹣×2×2=,
故答案为:.
【点评】本题考查了扇形的面积,勾股定理,直角三角形的性质的应用,解此题的关键是能正确求出扇形CEB′和三角形CDE的面积,题目比较好,难度适中.
16.(3分)(2017•营口)某市为绿化环境计划植树2400棵,实际劳动中每天植树的数量比原计划多20%,结果提前8天完成任务.若设原计划每天植树x棵,则根据题意可列方程为 ﹣=8 .
【分析】设原计划每天植树x棵,则实际每天植树(1+20%)x=1.2x,根据“原计划所用时间﹣实际所用时间=8”列方程即可.
【解答】解:设原计划每天植树x棵,则实际每天植树(1+20%)x=1.2x,
根据题意可得:﹣=8,
故答案为:﹣=8.
【点评】本题主要考查由实际问题抽象出分式方程,解题的关键是找到题目蕴含的相等关系.
17.(3分)(2017•营口)在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 3或6 .
【分析】由AD=8、AB=6结合矩形的性质可得出AC=10,△EFC为直角三角形分两种情况:①当∠EFC=90°时,可得出AE平分∠BAC,根据角平分线的性质即可得出=,解之即可得出BE的长度;②当∠FEC=90°时,可得出四边形ABEF为正方形,根据正方形的性质即可得出BE的长度.
【解答】解:∵AD=8,AB=6,四边形ABCD为矩形,
∴BC=AD=8,∠B=90°,
∴AC==10.
△EFC为直角三角形分两种情况:
①当∠EFC=90°时,如图1所示.
∵∠AFE=∠B=90°,∠EFC=90°,
∴点F在对角线AC上,
∴AE平分∠BAC,
∴=,即=,
∴BE=3;
②当∠FEC=90°时,如图2所示.
∵∠FEC=90°,
∴∠FEB=90°,
∴∠AEF=∠BEA=45°,
∴四边形ABEF为正方形,
∴BE=AB=6.
综上所述:BE的长为3或6.
故答案为:3或6.
【点评】本题考查了翻折变换、矩形的性质、角平分线的性质、正方形的判定与性质以及勾股定理,分∠EFC=90°和∠FEC=90°两种情况寻找BE的长度是解题的关键.
18.(3分)(2017•营口)如图,点A1(1,)在直线l1:y=x上,过点A1作A1B1⊥l1交直线l2:y=x于点B1,A1B1为边在△OA1B1外侧作等边三角形A1B1C1,再过点C1作A2B2⊥l1,分别交直线l1和l2于A2,B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2
,…按此规律进行下去,则第n个等边三角形AnBnCn的面积为 .(用含n的代数式表示)
【分析】由点A1的坐标可得出OA1=2,根据直线l1、l2的解析式结合解直角三角形可求出A1B1的长度,由等边三角形的性质可得出A1A2的长度,进而得出OA2=3,通过解直角三角形可得出A2B2的长度,同理可求出AnBn的长度,再根据等边三角形的面积公式即可求出第n个等边三角形AnBnCn的面积.
【解答】解:∵点A1(1,),
∴OA1=2.
∵直线l1:y=x,直线l2:y=x,
∴∠A1OB1=30°.
在Rt△OA1B1中,OA1=2,∠A1OB1=30°,∠OA1B1=90°,
∴A1B1=OB1,
∴A1B1=.
∵△A1B1C1为等边三角形,
∴A1A2=A1B1=1,
∴OA2=3,A2B2=.
同理,可得出:A3B3=,A4B4=,…,AnBn=,
∴第n个等边三角形AnBnCn的面积为×AnBn2=.
故答案为:.
【点评】本题考查了一次函数图象上点的坐标特征、解直角三角形以及等边三角形的性质,通过解直角三角形及等边三角形的性质,找出AnBn=是解题的关键.
三、解答题(19小题10分,20小题10分,共20分.)
19.(10分)(2017•营口)先化简,再求值:(﹣)÷(1﹣),其中x=()﹣1﹣(2017﹣)0,y=sin60°.
【分析】先根据分式的混合运算顺序和法则化简原式,再计算出x、y的值代入即可得.
【解答】解:原式=[﹣]÷
=•
=﹣,
当x=()﹣1﹣(2017﹣)0=3﹣1=2,y=sin60°=×=时,
原式=﹣=﹣4.
【点评】本题主要考查分式的化简求值,熟练掌握分式的混合运算顺序和法则是解题的关键.
20.(10分)(2017•营口)如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机
摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A、B、C、D表示).
【分析】(1)首先根据题意结合概率公式可得答案;
(2)首先根据(1)求得摸出两张牌面图形都是轴对称图形的有16种情况,若摸出两张牌面图形都是中心对称图形的有12种情况,继而求得小明赢与小亮赢的概率,比较概率的大小,即可知这个游戏是否公平.
【解答】解:(1)共有4张牌,正面是中心对称图形的情况有3种,所以摸到正面是中心对称图形的纸牌的概率是;
(2)列表得:
A
B
C
D
A
(A,B)
(A,C)
(A,D)
B
(B,A)
(B,C)
(B,D)
C
(C,A)
(C,B)
(C,D)
D
(D,A)
(D,B)
(D,C)
共产生12种结果,每种结果出现的可能性相同,其中两张牌都是轴对称图形的有6种,
∴P(两张都是轴对称图形)=,因此这个游戏公平.
【点评】本题考查的是游戏公平性的判断,以及概率.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.
四、解答题(21题12分,22小题12分,共24分)
21.(12分)(2017•营口)某中学开展“汉字听写大赛”活动,为了解学生的参与情况,在该校随机抽取了四个班级学生进行调查,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,解答下列问题:
(1)这四个班参与大赛的学生共 100 人;
(2)请你补全两幅统计图;
(3)求图1中甲班所对应的扇形圆心角的度数;[来源:学+科+网Z+X+X+K]
(4)若四个班级的学生总数是160人,全校共2000人,请你估计全校的学生中参与这次活动的大约有多少人.
【分析】(1)根据乙班参赛30人,所占比为20%,即可求出这四个班总人数;[来源:学_科_网]
(2)根据丁班参赛35人,总人数是100,即可求出丁班所占的百分比,再用整体1减去其它所占的百分比,即可得出丙所占的百分比,再乘以参赛得总人数,即可得出丙班参赛得人数,从而补全统计图;
(3)根据甲班级所占的百分比,再乘以360°,即可得出答案;
(4)根据样本估计总体,可得答案.
【解答】解:(1)这四个班参与大赛的学生数是:
30÷30%=100(人);
故答案为100;
(2)丁所占的百分比是:×100%=35%,
丙所占的百分比是:1﹣30%﹣20%﹣35%=15%,
则丙班得人数是:100×15%=15(人);
如图:
(3)甲班级所对应的扇形圆心角的度数是:30%×360°=108°;
(4)根据题意得:2000×=1250(人).
答:全校的学生中参与这次活动的大约有1250人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
22.(12分)(2017•营口)如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点A处测得码头C在船的东北方向,航行40分钟后到达B处,这时码头C恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头C的最近距离.(结果精确到0.1海里,参考数据≈1.41,≈1.73)
【分析】过点C作CE⊥AB于点E,过点B作BD⊥AC于点D,由题意可知:船在航行过程中与码头C的最近距离是CE,根据∠
DAB=30°,AB=20,从而可求出BD、AD的长度,进而可求出CE的长度.
【解答】解:过点C作CE⊥AB于点E,过点B作BD⊥AC于点D,
由题意可知:船在航行过程中与码头C的最近距离是CE,
AB=30×=20,
∵∠NAC=45°,∠NAB=75°,
∴∠DAB=30°,
∴BD=AB=10,
由勾股定理可知:AD=10
∵BC∥AN,
∴∠BCD=45°,
∴CD=BD=10,
∴AC=10+10
∵∠DAB=30°,
∴CE=AC=5+5≈13.7
答:船在航行过程中与码头C的最近距离是13.7海里
【点评】本题考查解三角形的应用,解题的关键是熟练运用锐角三角函数以及勾股定理,本题属于中等题型.
五、解答题(23小题12分,24小题12分,共24分)
23.(12分)(2017•营口)如图,点E在以AB为直径的⊙O上,点C是的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.
(1)求证:CD是⊙O的切线;
(2)若cos∠CAD=,BF=15,求AC的长.
【分析】(1)连接OC,由点C是的中点利用垂径定理可得出OC⊥BE,由AB是⊙O的直径可得出AD⊥BE,进而可得出AD∥OC,再根据AD⊥CD可得出OC⊥CD,由此即可证出CD是⊙O的切线.
(2)过点O作OM⊥AC于点M,由点C是的中点利用圆周角定理可得出∠BAC=∠CAE,根据角平分线的定理结合cos∠CAD=可求出AB的长度,在Rt△AOM中,通过解直角三角形可求出AM的长度,再根据垂径定理即可得出AC的长度.
【解答】(1)证明:连接OC,如图1所示.
∵点C是的中点,
∴=,
∴OC⊥BE.
∵AB是⊙O的直径,
∴AD⊥BE,
∴AD∥OC.[来源:Z&xx&k.Com]
∵AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线.
(2)解:过点O作OM⊥AC于点M,如图2所示.
∵点C是的中点,
∴=,∠BAC=∠CAE,
∴=.
∵cos∠CAD=,
∴=,
∴AB=BF=20.
在Rt△AOM中,∠AMO=90°,AO=AB=10,cos∠OAM=cos∠CAD=,
∴AM=AO•cos∠OAM=8,
∴AC=2AM=16.
【点评】本题考查了切线的判定与性质、解直角三角形、平行线的性质、垂径定理、圆周角定理以及角平分线的性质,解题的关键是:(1)根据平行线的性质找出OC⊥CD;(2)根据角平分线的性质求出AB的长度.
24.(12分)(2017•营口)夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第x天生产空调y台,直接写出y与x之间的函数解析式,并写出自变量x的取值范围.
(2)若每台空调的成本价(日生产量不超过50台时)为2000元,订购价格为每台2920元,设第x天的利润为W元,试求W与x之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.
【分析】(1)根据接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,直接得出生产这批空调的时间为x天,与每天生产的空调为y台之间的函数关系式;
(2)根据基本等量关系:利润=(每台空调订购价﹣每台空调成本价﹣增加的其他费用)×生产量即可得出答案.
【解答】解:(1)∵接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,
∴由题意可得出,第x天生产空调y台,y与x之间的函数解析式为:y=40+2x(1≤x≤10);
(2)当1≤x≤5时,W=(2920﹣2000)×(40+2x)=1840x+36800,
∵1840>0,
∴W随x的增大而增大,
∴当x=5时,W最大值=1840×5+36800=46000;
当5<x≤10时,
W=[2920﹣2000﹣20(40+2x﹣50)]×(40+2x)=﹣80(x﹣4)2+46080,
此时函数图象开口向下,在对称轴右侧,W随着x的增大而减小,又天数x为整数,
∴当x=6时,W最大值=45760元.
∵46000>45760,
∴当x=5时,W最大,且W最大值=46000元.
综上所述:W=.
【点评】此题主要考查了二次函数的应用以及分段函数,如何分段,怎样表达每个分段函数,并比较确定最大值是解本题的关键.
六、解答题(本题满分14分)
25.(14分)(2017•营口)在四边形中ABCD,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)若四边形ABCD为正方形.
①如图1,请直接写出AE与DF的数量关系 DF=AE ;
②将△EBF绕点B逆时针旋转到图2所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由;
(3)如图3,若四边形ABCD为矩形,BC=mAB,其它条件都不变,将△EBF绕点B顺时针旋转α(0°<α<90°)得到△E'BF',连接AE',DF',请在图3中画出草图,并直接写出AE'与DF'的数量关系.
【分析】(1)①利用正方形的性质得△ABD为等腰直角三角形,则BF=AB,再证明△BEF为等腰直角三角形得到BF=BE,所以BD﹣BF=AB﹣BE,从而得到DF=AE;
②利用旋转的性质得∠ABE=∠DBF,加上==,则根据相似三角形的判定可得到△ABE∽△DBF,所以==;
(2)先画出图形得到图3,利用勾股定理得到BD=AB,再证明△BEF∽△BAD得到=,则==,接着利用旋转的性质得∠ABE′=∠DBF′,BE′=BE,BF′=BF,所以==,然后根据相似三角形的判定方法得到△ABE′∽△DBF′,再利用相似的性质可得==.
【解答】解:(1)①∵四边形ABCD为正方形,
∴△ABD为等腰直角三角形,
∴BF=AB,
∵EF⊥AB,
∴△BEF为等腰直角三角形,
BF=BE,
∴BD﹣BF=AB﹣BE,
即DF=AE;
故答案为DF=AE;
②DF=AE.理由如下:
∵△EBF绕点B逆时针旋转到图2所示的位置,
∴∠ABE=∠DBF,
∵=,=,
∴=,
∴△ABE∽△DBF,
∴==,
即DF=AE;
(2)如图3,∵四边形ABCD为矩形,
∴AD=BC=mAB,
∴BD==AB,
∵EF⊥AB,
∴EF∥AD,
∴△BEF∽△BAD,
∴=,
∴==,
∵△EBF绕点B顺时针旋转α(0°<α<90°)得到△E'BF',
∴∠ABE′=∠DBF′,BE′=BE,BF′=BF,
∴==,
∴△ABE′∽△DBF′,
∴==,
即DF′=AE′.
【点评】本题考查了相似形的综合题:熟练掌握旋转的性质、矩形和正方形的性质;灵活应用相似三角形的判定和性质,会利用相似比表示线段之间的关系.
七、解答题(本题满分14分)
26.(14分)(2017•营口)如图,抛物线y=ax2+bx﹣2的对称轴是直线x=1,与x轴交于A,B两点,与y轴交于点C,点A的坐标为(﹣2,0),点P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E.
(1)求抛物线解析式;
(2)若点P在第一象限内,当OD=4PE时,求四边形POBE的面积;
(3)在(2)的条件下,若点M为直线BC上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点B,D,M,N为顶点的四边形是菱形?若存在上,直接写出点N的坐标;若不存在,请说明理由.
【温馨提示:考生可以根据题意,在备用图中补充图形,以便探究】
【分析】(1)由抛物线y=ax2+bx﹣2的对称轴是直线x=1,A(﹣2,0)在抛物线上,于是列方程即可得到结论;
(2)根据函数解析式得到B(4,0),C(0,﹣2),求得BC的解析式为y=x﹣2,设D(m,0),得到E(m,m﹣2),P(m,m2﹣m﹣2),根据已知条件列方程得到m=5,m=0(舍去),求得D(5,0),P(5,),E(5,),根据三角形的面积公式即可得到结论;
(3)设M(n,n﹣2),①以BD为对角线,根据菱形的性质得到MN垂直平分BD,求得n=4+,于是得到N(,﹣);②以BD为边,根据菱形的性质得到MN∥BD,MN=BD=MD=1,过M作MH⊥x轴于H,根据勾股定理列方程即可得到结论.
【解答】解:(1)∵抛物线y=ax2+bx﹣2的对称轴是直线x=1,A(﹣2,0)在抛物线上,∴,解得:,抛物线解析式为y=x2﹣x﹣2;[来源:Zxxk.Com]
(2)令y=x2﹣x﹣2=0,解得:x1=﹣2,x2=4,当x=0时,y=﹣2,∴B(4,0),C(0,﹣2),设BC的解析式为y=kx+b,则,解得:,∴y=x﹣2,
设D(m,0),
∵DP∥y轴,
∴E(m,m﹣2),P(m,m2﹣m﹣2),
∵OD=4PE,
∴m=4(m2﹣m﹣2﹣m+2),
∴m=5,m=0(舍去),
∴D(5,0),P(5,),E(5,),
∴四边形POBE的面积=S△OPD﹣S△EBD=×5×﹣1×=;
(3)存在,设M(n,n﹣2),
①以BD为对角线,如图1,
∵四边形BNDM是菱形,
∴MN垂直平分BD,
∴n=4+,
∴M(,),
∵M,N关于x轴对称,
∴N(,﹣);
②以BD为边,如图2,
∵四边形BNDM是菱形,
∴MN∥BD,MN=BD=MD=1,
过M作MH⊥x轴于H,
∴MH2+DH2=DM2,
即(n﹣2)2+(n﹣5)2=12,
∴n1=4(不合题意),n2=5.6,
∴N(4.6,),
同理(n﹣2)2+(4﹣n)2=1,
∴n1=4+(不合题意,舍去),n2=4﹣,
∴N(5﹣,﹣),
③以BD为边,如图3,
过M作MH⊥x轴于H,
∴MH2+BH2=BM2,
即(n﹣2)2+(n﹣4)2=12,
∴n1=4+,n2=4﹣(不合题意,舍去),
∴N(5+,),
综上所述,当N(,﹣)或(4.6,)或(5﹣,﹣)或(5+,),以点B,D,M,N为顶点的四边形是菱形.
【点评】本题主要考查的是二次函数的综合应用,本题主要涉及了待定系数法求一次函数、二次函数的解析式、勾股定理,三角形的面积公式、菱形的性质、根据题意画出符合条件的图形是解题的关键.
相关文档
- 2013年云南德宏州中考数学试卷及答2021-11-128页
- 2019四川省绵阳中考数学试卷(word版2021-11-1223页
- 2018年湖北省仙桃市中考数学试卷2021-11-1230页
- 2018年山东省滨州市中考数学试卷2021-11-1226页
- 2014年上海市中考数学试卷(含答案)2021-11-1210页
- 2014年江苏省扬州市中考数学试卷(2021-11-1221页
- 2014年内蒙古包头市、乌兰察布市中2021-11-1219页
- 2020年湖北省黄石市中考数学试卷【2021-11-129页
- 2020年浙江省台州市中考数学试卷【2021-11-1213页
- 2019年上海市中考数学试卷2021-11-1227页