三年级数学思维训练整套 112页

三年级数学思维训练整套 三年级数学思维训练：数图形一 三年级数学思维训练：数图形二 三年级数学思维训练：数图形三 三年级数学思维训练：数图形四 三年级数学思维训练：数图形五 三年级数学思维训练：找规律一 三年级数学思维训练：找规律二 三年级数学思维训练：找规律三 三年级数学思维训练：找规律四 三年级数学思维训练：找规律五 三年级数学思维训练：加减巧算1‎ 三年级数学思维训练：加减巧算2‎ 三年级数学思维训练：加减巧算3‎ 三年级数学思维训练：加减巧算4‎ 三年级数学思维训练：加减巧算5‎ 三年级数学思维训练：添运算符号1‎ 三年级数学思维训练：添运算符号2‎ 三年级数学思维训练：添运算符号3‎ 三年级数学思维训练：添运算符号4‎ 三年级数学思维训练：添运算符号5‎ 三年级数学思维训练：算式谜 三年级数学思维训练：文字算式谜 六年级数学思维训练：简便运算三，用拆分法进行分数的简便运算 三年级数学思维训练：填数游戏 三年级数学思维训练：有余除法 三年级数学思维训练：周期问题 三年级数学思维训练：数学趣题 三年级数学思维训练：配对求和 三年级数学思维训练：乘法速算 三年级数学思维训练：应用题（一）‎ 三年级数学思维训练：乘除巧算 三年级数学思维训练：应用题（二）‎ 三年级数学思维训练：植树问题 三年级数学思维训练：数字趣谈 三年级数学思维训练：重叠问题 三年级数学思维训练：简单枚举 三年级数学思维训练：等量代换 三年级数学思维训练：错中求解 三年级数学思维训练：用对应法解题 三年级数学思维训练：盈亏问题 三年级数学思维训练：简单枚举 ‎1‎ 专题简析：‎ 枚举是一种常见的分析问题、解决问题的方法。一般地，要根据问题要求，一一列举问题解答。运用枚举法解应用题时，必须注意无重复、无遗漏，因此必须有次序、有规律地进行枚举。运用枚举法解题的关键是要正确分类，要注意以下两点：一是分类要全，不能造成遗漏；二是枚举要清，要将每一个符合条件的对象都列举出来。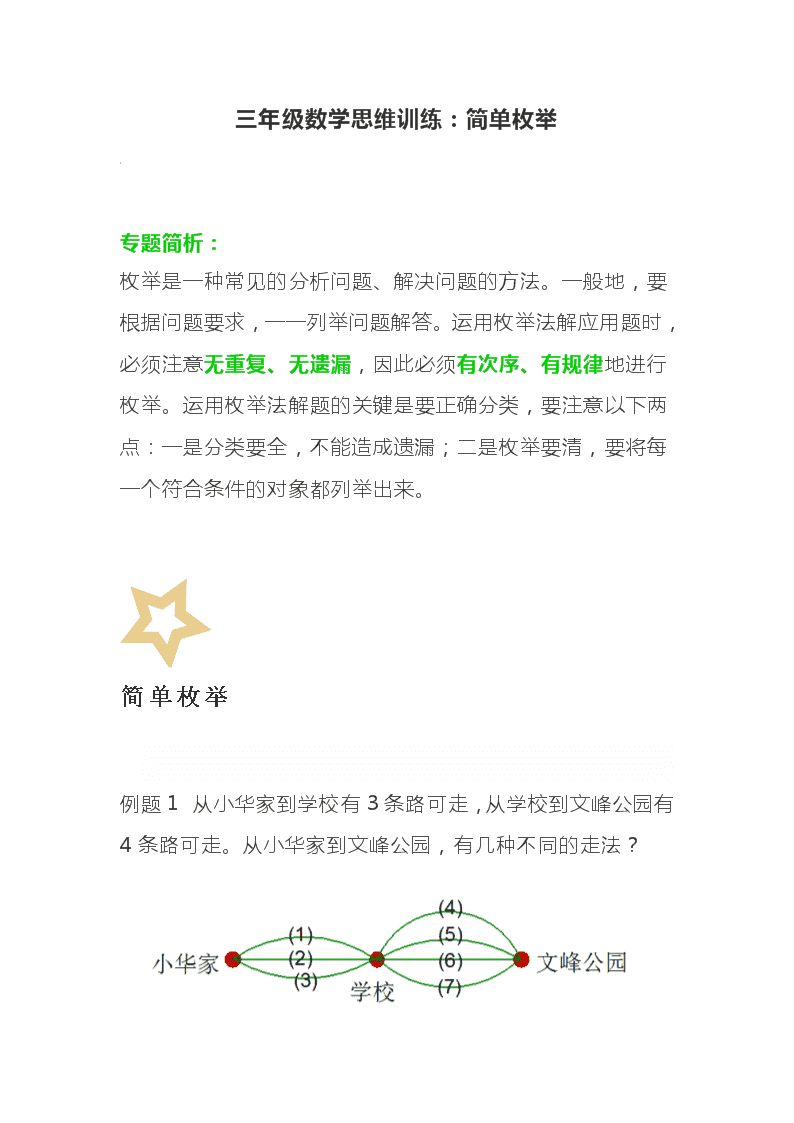‎ ‎ ‎ 简单枚举 例题1  从小华家到学校有3条路可走，从学校到文峰公园有4条路可走。从小华家到文峰公园，有几种不同的走法？‎ 为了帮助理解题意，我们可以画出如上示意图。 我们把小华的不同走法一一列举如下：‎ 根据列举可知，从小明家经学校到文峰公园，走①路有4种不同走法，走②路有4种不同走法，走③路也有4种不同走法，共有4×3=12种不同走法。‎ ‎01‎ 小试牛刀 ‎1，从甲地到乙地，有3条公路直达，从乙地到丙地有2条铁路直达。从甲地到丙地有多少种不同走法？2，新华书店有3种不同的英语书，4种不同的数学读物销售。小明想买一种英语书和一种数学读物，共有多少种不同买法？3，明明有2件不同的上衣，3条不同的裤子，4双不同的鞋子。最多可搭配成多少种不同的装束？‎ 例题2  用红、绿、黄三种信号灯组成一种信号，可以组成多少种不同的信号？思路导航：要使信号不同，要求每一种信号颜色的顺序不同，我们可以把这些信号进行列举：‎ 从上面可以看出：红色信号灯排在第一个位置时，有两种不同的信号，绿色信号灯排在第一个位置时，也有两种不同的信号，黄色信号灯排在第一个位置时，也有两种不同的信号，因而共有3个2种不同排列方法，即2×3=6种。‎ ‎02‎ 小试牛刀 ‎1，用红、黄、蓝三种颜色涂圆圈，每个圆圈涂一种颜色，一共有多少种不同的涂法？○○○2，用数字1、2、3，可以组成多少个不同的三位数？分别是哪几个数？3，用2、3、5、7四个数字，可以组成多少个不同的四位数？‎ 例题3  一个长方形的周长是22米，如果它的长和宽都是整米数，那么这个长方形的面积有多少种可能？思路导航：由于长方形的周长是22米，可知它的长与宽之和为11米。下面列举出符合这个条件的各种长方形：‎ ‎03‎ 小试牛刀 ‎1，一个长方形的周长是30厘米，如果它的长和宽都是整厘米数，那么这个长方形的面积有多少种可能值？2，把15个玻璃球分成数量不同的4堆，共有多少种不同的分法？3，3个自然数的乘积是18，问由这样的3个数所组成的数组有多少个？如（1，2，9）就是其中的一个，而且数组中数字相同但顺序不同的算作同一数组，如（1，2，9）和（2，9，1）是同一数组。‎ 例题4  有4位小朋友，寒假中互相通一次电话，他们一共打了多少次电话？思路导航：把4个小朋友分别编号：A、B、C、D，A与其他小朋友打电话，应该打3次，同样B小朋友也应打3次电话，同样C、D应该各打3次电话。4个小朋友，共打了3×4=12次。但题目要求两个小朋友之间只要通一次电话，那么A打电话给B时，A、B两人已经通过话了，所以B没有必要再打电话给A，照这样计算，12次电话中，有一半是重复计算的，所以实际打电话的次数是3×4÷2=6次。‎ ‎04‎ 小试牛刀 ‎1，6个小队进行排球比赛，每两队比赛一场，共要进行多少次比赛？2，有8位小朋友，要互通一次电话，他们一共打了多少次电话？3，小芳出席由19人参加的联欢会，散会后，每两人都要握一次手，他们一共握了多少次手？‎ 例题5  一条铁路，共有10个车站，如果每个起点站到终点站只用一种车票（中间至少相隔5个车站），那么这样的车票共有多少种？‎ 我们可以利用列举的方法： 如果起点站是1，那么终点站只能是7、8、9或10；如果起站站是2，那么终点站只能是8、9或10；如果起点站是3，那么终点站只能是9或10；如果起点站是4，终点站只能是10；如果起点站是5、6时，就找不到与它至少相隔5站的终点站了；如果起点站是7，终点站只能是1；如果起点站是8，那么终点站是2或1；如果起点站是9，那么终点站是3、2或1；如果起点站是10，那么终点站是4、3、2或1。所以，起点到终点至少相隔5个车站的车票有：4＋3＋2＋1＋0＋0＋1＋2＋3＋4=20种。‎ ‎05‎ 小试牛刀 ‎1，上海、北京、天津三个城市分别设有一个飞机场，它们之间通航一共需要多少种不同的机票？2，一条公路上，共有8个站点。如果每个起点到终点只用一种车票（中间至少相隔3个车站），那么共有多少种不同的车票？3，在长江的某一航线上共有6个码头，如果每个起点终点只许用一种船票（中间至少要相隔2个码头），那么这样的船票共有多少种？‎ 三年级数学思维训练：错中求解 ‎1‎ 专题简析：‎ 在进行加、减、乘、除运算时，要认真审题，不能抄错题目，不能漏掉数字。计算时要仔细小心，不能丝毫马虎，否则就会造成错误。解答这类题，往往要采用倒推的方法，从错误的结果入手分析错误的原因，最后利用和差的变化求出加数或被减数、减数，利用积、商的变化求出因数或被除数、除数。‎ ‎ ‎ 错中求解 例题1  小马虎在做一道加法题时，把一个加数十位的5错看成2，另一个加数个位上的4错看成1，结果计算的和为241。正确的和是多少？思路导航：把一个加数十位上的5看成2，少了3个10，这样和就减少了30；把另一个加数个位上的4看作1，少了3个1，这样和就少了3。小马虎算出的和比原来的和少了30＋3=33，所以正确的和是241＋33=274。‎ ‎01‎ 小试牛刀 1， 小明在做一道加法时，把一个加数个位上的2看作了4，另一个加数个位上的7看作9，结果计算的和为215。正确的和为多少？‎ 2， 小马虎在做一道加法题时，把一个加数个位上的3看作了5，十位上的4看作7，得到结果为376。正确的和是多少？‎ ‎，小粗心在计算一道加法题时，把一个加数个位上的7看作1，十位上的3看作8，结果为342。正确的和是多少？‎ 例题2  小马虎在做一道减法时，把减数十位上的2看作了5，结果得到的差是342，正确的差是多少？思路导航：十位上的2表示2个十，十位上的5表示5个十，把十位上的2看作5，就是把20看作50，减数从20变为50，增加了30，所得的差减少了30，应在342中增加30，才是正确的差。340＋30=372‎ ‎02‎ 小试牛刀 1， 小马虎在做减法题时，把被减数十位上的3错写成8，结果得到的差是284。正确的差是多少？‎ 2， 在减法算式中，错把减数个位上的3写成了5，结果得到的差是254。正确的差是多少？‎ ‎3，小丽在做一道减法时，错把被减数十位上的2看作7，减数个位上的5看作8，结果得到的差是592。正确的差是多少？‎ 例题3  小马虎在计算一道题目时，把某数乘3加20，误看成某数除以3减20，得数是72。某数是多少？正确的得数是多少？思路导航：小马虎计算得到72，是先除再减得到的，我们可以根据逆运算的顺序把72先加后乘，求出某数为（72＋20）×3=276，然后再按题目要求，按运算顺序求出正确的数276×3＋20=848。‎ ‎03‎ 小试牛刀 1， 小丽在计算一道题时，把某数乘4加20，误看成除以4减20，得数为35。某数是多少？正确的结果是多少？‎ 2， 小粗心在计算时，把一个数除以2减4，误看成乘2加上4，得数是36。正确结果是多少？‎ ‎3，小华在计算一道题时，把一个数加上4乘2看作了乘2加上4，得数为40。正确的得数是多少？‎ 例题4  小马虎在做两位数乘两位数的题时，把乘数的个位上的5看作2，乘得的结果是550，实际应为625。这两个两位数各是多少？思路导航：我们可以用竖式来帮助分析：乘数个位上的5看作2，结果比原来少了5－2=3个被乘数，实际的结果与错误的结果相差625－550=75；75正好是被乘数的3倍，被乘数是75÷3=25，乘数是625÷25=25。‎ ‎04‎ 小试牛刀 1， 一位学生在做两位数乘法时，把乘数个位上的8错写成4，乘得的结果是1080，实际应为1260。这两个两位数分别为多少？‎ 1， 小华在做一道两位数乘法时，把乘数个位上的3错写成5，乘得的结果是875，正确的结果是805。这两个两位数分别是多少？‎ ‎3，小芳在计算一道题时，把5×（△＋7）错写成5×△＋7，她得到的结果与正确答案相差多少？‎ 例题5  小林在计算有余数除法时，把被除数137当作173，结果商比正确结果大了4，但余数恰好相同。正确的除法算式应是什么？思路导航：把被除数137当作173，被除数就多了173－137=36，因此商比正确结果大4，但余数相同，说明除数的4倍就是36。所以除数为36÷4=9，正确的除法算式为137÷9=15……2。‎ ‎05‎ 小试牛刀 1， 小红在计算有余数除法时，把被除数113错写成131，这样商比原来多2，但余数恰好相同。正确的除数和余数是多少？‎ 1， 王刚在计算有余数除法时，把被除数171错写成117，结果商比原来少9，但余数恰好相同。正确的除法算式是怎样的？‎ ‎3，小明在计算除法时，把被除数末尾的0漏写而成18，结果得到的商比正确的商少54。正确的除法算式是什么？‎ 三年级数学思维训练：用对应法解题 ‎1‎ 专题简析：‎ 小朋友在解答应用题时，经常会碰到这样一类题，给定的数量和所对应的数量关系是在变化的。为了使变化的数量看得更清楚，可以把已知条件按照它们之间的对应关系排列出来，进行观察和分析，从而找到答案。这种解题的思维方法叫对应法。在用对应法解题时，通常先把题目中的数量关系转化为等式，并把这些等式按顺序编号，然后认真观察，比较对应关系的变化，以便寻找解题的突破口。‎ ‎ ‎ 用对应法解题 例题1  奶奶去买水果，如果她买4千克梨和5千克荔枝，需花58元；如果她买6千克梨和5千克荔枝，那么需花62元。问1千克梨和1千克荔枝各多少元？思路导航：我们可以把两次买的情况摘录下来进行比较：4千克梨＋5千克荔枝=58元    （1）6千克梨＋5千克荔枝=62元    （2）比较（1）和（2）式，发现两式中荔枝的千克数相等，（2）式比（1）式多了6－4=2千克梨，也就是多了62－58=4元，说明1千克梨的价钱为4÷2=2元，那么1千克荔枝的价钱就是（58－2×4）÷5=10元。‎ ‎01‎ 小试牛刀 ‎1，3筐苹果和5筐橘子共重270千克，3筐苹果和7筐橘子共重342千克。一筐苹果和一筐橘子各重多少千克？‎ 2， 张老师为图书室买书，如果他买6本童话书和7本故事书需要144元；如果买9本童话书和7本故事书，需要174元。现在张老师买7本童话书和6本故事书，共需多少元 ‎3，粮店运来一批粮食，4袋大米和5袋面粉共重600千克，2袋大米和3袋面粉共重340千克。一袋大米和一袋面粉各重多少千克？‎ 例题2  学校买足球和排球，买3个足球和4个排球共需要190元，如果买6个足球和2个排球需要230元。一个足球和一个排球各多少元？思路导航：我们可以把两次买的情况摘录下来进行比较：3个足球＋4个排球=190元    （1）6个足球＋2个排球=230元    （2）我们把（1）、（2）两式进行比较，发现两组条件相加还是相减，都不可能求出足球和排球的单价，因为这里没有一个相同的条件可减去。再观察我们可以发现：如果把（1）式同时扩大2倍，得到6个足球和8个排球共380元，然后再与（2）式进行比较，发现足球个数相同，而排球多了6个，也就多了380－230=150元，也就是6个排球是150元，一个排球为150÷6=25元，那么一个足球是（190－25×4）÷3=30元。‎ ‎02‎ 小试牛刀 ‎1，5筐番茄和2筐黄瓜共重330千克，3筐番茄和4筐黄瓜共重310千克。一筐番茄和一筐黄瓜各重多少千克？‎ ‎2，4本练习本和5枝圆株笔共14元，2本练习本和4枝圆珠笔共10元。一本练习本和一枝圆珠笔各多少元？‎ ‎3，2件上衣和3条裤子共480元，4件上衣和2条裤子共640地。一件上衣和一条裤子各多少元？‎ 例题3  商店里有一些气球，其中红气球和蓝气球共21只，蓝气球和黄气球共28只，黄气球和红气球共29只。红气球、蓝气球和黄气球各有多少只？思路导航：根据题意，我们可以列出下列关系式：红气球的个数＋蓝气球的个数=21    （1）蓝气球的个数＋黄气球的个数=28    （2）黄气球的个数＋红气球的个数=29    （3）我们可将（1）＋（2）＋（3），即21＋28＋29=78只，这里包含有2倍红气球的个数、2倍蓝气球的个数和2倍黄气球的个数，由此，可得出三种气球的总只数：78÷2=39只。然后再根据红气球和蓝气球共21只，可求出黄气球的只数：39－21=18只；同理可求出红气球的个数是39×28=11只，蓝气球的个数是39－29=19只。‎ ‎03‎ 小试牛刀 1， 小明和小红共12岁，小红和小丽共17岁，小丽和小明共13岁。三人各多少岁？‎ 2， 新华书店有批书，故事书和连环画共70本，连环画和科技书共82本，科技书和故事书共76本。三种书各多少本？‎ ‎3，公园开菊花展，白菊花和黄菊花共152盆，黄菊花和红菊花共128盆，红菊花和白菊花共168盆。三种菊花各几盆？‎ 例题4  三年级三个班种了一片小树林，其中72棵不是一班种的，75棵不是二班种的，73棵不是三班种的。三个班各种了多少棵？思路导航：“72棵不是一班种的”，说明二班和三班共种树72棵；“75棵不是二班种的”，说明一班和三班共种75棵，“73棵不是三班种的”，说明一班和二班共种73棵。这样，我们就可以求出三个班共种多少棵树：（72＋75＋73）÷2=110棵。用110－72=38棵就是一班种的棵数，110－75=35棵就是二班种的棵数，110－73=37棵就是三班种的棵数。‎ ‎04‎ 小试牛刀 1， 百货商店运来三种鞋子，其中37双不是皮鞋，54双不是运动鞋，51双不是布鞋。三种鞋各运来多少双？‎ 2， 一个班同学在做作业，班主任问后得知：全班同学都只做完了语文、数学英语作业其中的一种。有23人没有做完数学作业，有19人没有做完语文作业，有16人没有做完英语作业。做完三种作业的各多少人？‎ ‎3，学校买四种颜色的气球，其中有93个不是红气球，有95个不是黄气球，有98个不是蓝气球，紫气球有10个。学校共买了多少个气球？‎ 例题5  已知13个李子的重量等于2个苹果和1个桃子的重量，而4个李子和1个苹果的重量等于1个桃子的重量。问多少个李子的重量等于1个桃子的重量？思路导航：根据题意列出等式：13李=2苹＋1桃    （1）4李＋1苹=1桃    ‎ ‎ （2）把（2）式代入（1）式得：13李=2苹＋4李＋1苹即9李=3苹，即3李=1苹    （3）把（3）式代入（2）式得：4李＋3李=1桃    即：7李=1桃 ‎05‎ 小试牛刀 ‎1，3个菠萝的重量等于1个梨和1个西瓜的重量，而1个菠萝和3个梨的重量等于1个西瓜的重量。问多少个梨的重量等于1个西瓜的重量？‎ ‎2，2个苹果的重量等于3个橘子和3个荔枝的重量，1个苹果和2个荔枝的重量等于3个橘子的重量。问3个橘子的重量等于多少个荔枝的重量？‎ ‎3，三个好朋友去文具店买东西，一人买了4枝圆珠笔，一个买了2枝钢笔，还有一个买了1枝钢笔1枝圆珠笔和4枝铅笔，三个人用掉的钱相等。那么1枝钢笔的价钱相当于几枝铅笔的价钱？‎ 三年级数学思维训练：盈亏问题 ‎1‎ 专题简析：‎ 把一定数量的物品，平均分给一定数量的人，每人少分，则物品有余（盈）；每人多分，则物品不足（亏）。已知所盈和所亏的数量，求物品数量和人数的应用题叫盈亏问题。盈亏问题的基本解法是：份数=（盈＋亏）÷两次分配数的差，物品数可由其中一种分法的份和盈亏数求出。解答盈亏问题的关键是要求出总差额和两次分配的数量差，然后利用基本公式求出分配者人数，进而求出物品的数量。‎ ‎ ‎ 盈亏问题 例题1  小明的妈妈买回一篮梨，分给全家。如果每人分5个，就多出10个；如果每人分6个，就少2个。小明全家有多少人？这篮梨有多少个？思路导航：根据题目中的条件，我们可知：第一种分法：每人分5个，多10个；第二种分法：每人分6个，少2个。这说明全家人数为：10＋2=12人，也就是说：不足的个数＋多余的个数=全家的人数这篮梨的个数是：5×12＋10=70个；‎ ‎01‎ 小试牛刀 1， 幼儿园阿姨把一袋糖分给小朋友们，如果每人分10粒糖，则多了8粒糖；如果每人分11粒糖，则少了16粒糖。一共有多少个小朋友？这袋糖有多少粒？‎ 2， ‎2，有一根绳子绕树4圈，余2米；如果绕树5圈，则差6米。树周长是多少米？绳子长多少米？‎ 3， ‎3，一些同学去划船，如果每条船坐5人，则多出3个位置；如果每条船坐4人，则有3个人没有位置。一共有多少条船？一共有多少个同学？‎ 例题2  幼儿园买来一些玩具，如果每班分8个玩具，则多出2个玩具；如果每班分10个玩具，则少12个玩具。幼儿园有几个班？这批玩具有多少个？思路导航：根据题目中的条件，我们可知：第一种分法：每班分8个，多2个；第二种分法：每班分10个，少12个。从上面的条件中，我们可看出：第二种分法比第一种分法每班多分10－8=2个，所以，所需的玩具总个数从多2个变成了少12个，也就是说在多2个的基础上再加12个，才能保证每班分10个；第二种分法所需的玩具个数比第一种多12＋2=14个，那是因为每班多分了2个。根据这一对应关系，即可求出班级的个数为：14÷2=7个，玩具的总个数为8×7＋2=58个。‎ ‎02‎ 小试牛刀 1， 小明带了一些钱去买苹果，如果买3千克，则多出2元；如果买6千克，则少了4元。苹果每千克多少元？小明带了多少钱？‎ 2， 一个小组去山坡植树，如果每人栽4棵，还剩12棵；如果每人栽8棵，则缺4棵。这个小组有几人？一共有多少棵树苗？‎ 3， 一组学生去搬书，如果每人搬2本，还剩下12本；如果每人搬3本，还剩下6本。这组学生有几人？这批书有几本？‎ 例题3  老师买来一些练习本分给优秀少先队员，如果每人分5本，则多了14本；如果每人分7本，则多了2本。优秀少先队员有几人？买来多少本练习本？思路导航：根据题目中的条件，我们可知：第一种分法：每人5本，多了14本；第二种分法：每人7本，多了2本。从上面可知第二种分法比第一种分法每人多分了7－5=2本，这样就从原来的多14本变为多2本，两种分配方法的结果相差了14－2=12本，每人多分了2本，多少人会多分了12本呢？根据这一对应关系，可求出优秀少先队员的人数为12÷2=6人，练习本的本数为：5×6＋14=44本。‎ ‎03‎ 小试牛刀 1， 把一袋糖分给小朋友们，如果每人分4粒，则多了12粒；如果每人分6粒，则多了2粒。有小朋友几人？有多少粒糖？‎ 2， ‎2，妈妈买来一些苹果分给全家人，如果每人分6个，则多了12个；如果每人分7个，则多了6个。全家有几人？妈妈共买回多少个苹果？‎ 3， ‎3，某学校有一些学生住校，每间宿舍住8人，则空出床位24张；如果每间宿舍住10人，则空出床位2张。学校共有几间宿舍？住宿学生有几人？‎ 例题4‎ ‎  学校派一些学生去搬一批树苗，如果每人搬6棵，则差4棵；如果每人搬8棵，则差18棵。学生有几人？这批树苗有多少棵？思路导航：根据题意，我们可知搬树苗的两种方案：第一种方案：每人搬6棵，差4棵；第二种方案：每人搬8棵，差18棵。比较两种方案，每人多搬了8－6=2棵树苗，所需的树苗就从差4棵变为差18棵，结果相差了18－4=14棵，每人多搬了2棵，多少人会多搬了14棵呢？根据这一对应关系，可以求出学生人数为：14÷2=7人，树苗的棵数为：6×7－4=38棵。‎ ‎04‎ 小试牛刀 1， 自然课上，老师发给学生一些树叶。如果每人分5片叶子，则差3片叶子；如果每人分7片叶子，则差25片树叶。学生有几人？一共有树叶多少片？‎ 2， 数学兴趣小组的同学做数学题，如果每人做6道，则少4道；如果每人做8道，则少16道。有几个学生？多少道数学题？‎ 3， ‎3，学校排练节目，如果每行排8人，则有一行少2人；如果每行排9人，则有一行少7人。一共要排几行？一共有多少人？‎ 例题5‎ ‎  三（1）班学生去公园划船，如果每条船坐4人，则少一条船；如果每条船坐6人，则多出4条船。公园里有多少条船？三（1）班有多少学生？为了帮助理解，我们可以将题目中的条件进行转化。将条件“如果每条船坐4人，则少一条船”转化为：“如果每条船坐4人，则多出4人”；再将条件“如果每条船坐6人，则多出4条船”转化为：“如果每条船坐6人，则差6×4=24人”。这样两种分配方法就相差了24＋4=28人，这是因为每条船多坐了6－4=2人。根据这一关系，可求出船的条数：28÷2=14条，学生人数：4×（14＋1）=60人。‎ ‎05‎ 小试牛刀 1， 学校给新生分配宿舍，如果每间住8人，则少2间房；如果每间住10人，则多出2间房。共有几间房？新生有多少人？‎ ‎2，同学们去划船，如果每条船坐5人，则少2条船；如果每船坐7人，则多出2条船。共有几条船？有多少个同学？3，小明从家到学校，如果每分钟走40米，则要迟到2分钟；如果每分钟走50米，则早到4分钟。小明家到学校有多远？‎ 三年级数学思维训练：和差问题 和差问题 ‎ ‎ 专题简析：已知大小两个数的和及它们的差，求这两个数各是多少，这类问题我们称为和差问题。掌握了和差问题的特征和规律，我们解答起来就很方便了。解答和差问题通常用假设法，同时结合线段图进行分析。可以假设小数增加到与大数同样多，先求大数，再求小数；也可以假设大数减少到与小数同样多，先求小数，再求大数。用数量关系表示：（和＋差）÷2=大数（和－差）÷2=小数 例题1  期中考试王平和李杨语文成绩的总和是188分，李杨比王平少4分。两人各考了多少分？思路导航：根据题意画出线段图。‎ 我们可以用假设法来分析。假设李杨的分数和王平一样多，则总分就增加4分，变为188+4=192分，这就表示王平的2倍，所以王平考了：192÷2=96分，李杨考了96－4=92分。‎ 练  习  一 1， 两筐水果共重124千克，第一筐比第二筐多8千克。两筐水果各重多少千克？‎ 2， 3， 4， 5， ‎2，小宁与小慧的身高总和是264厘米，又已知小宁比小慧矮8厘米。两人分别高多少厘米？‎ 6， 7， 8， 1， ‎3，三（1）班和三（2）班共有学生124人，如果从三（2）班调2人到三（1）班，两班学生同样多。三（1）班、三（2）班原来各有学生多少人？‎ 例题2  某机床厂第一、二两个车间共有车床96部，如果第一车间拨给第二车间8部，那么两个车间车床数相等。两个车间各有车床多少部？思路导航：用线段图表示题意。‎ 已知第一、二两个车间共有车床96部，又根据“如果第一车间拨给第二车间8部，两个车间车床数相等”，从线段图上我们可以看出第一车间原来比第二车间多8×2=16部车床。所以，第一车间原有：（96+8×2）÷2=56部，第二车间原有56－8×2=40部。‎ 练  习  二1，红星小学一年级新108人，分成甲、乙两个班。如果从甲班转3个学生到乙班去，两班学生就一样多。甲、乙两班各有学生多少人？‎ 2， 甲、乙两筐共有水果80千克，若从甲箱取出6千克放到乙箱中，这时两箱水果同样多。两箱原来各有水果多少千克？‎ 3， 4， 5， 6， ‎3，有三只船共运木板9800块，第一只船比其余两船共运的少1400块，第二只船比第三只船少运200块。三只船各运木板多少块？‎ 例题3  哥弟俩共有邮票70张，如果哥哥给弟弟4张邮票，这时哥哥还比弟弟多2张。哥哥和弟弟原来各有邮票多少张？思路导航：我们可以这样想，哥弟俩共有邮票70张，根据“如果哥哥给弟弟4张，还比弟弟多2张”，说明原来哥哥比弟弟多4×2＋2=10张邮票。所以，弟弟有邮票：（70－10）÷2=30张，哥哥有邮票30+10=40张。‎ ‎ 练  习  三 1， 一只两层书架共放书72本，若从上层中拿出9本给下层，上层比下层多4本。上、下层各放书多少本？‎ 2， 3， 1， 2， ‎2，姐姐和妹妹共有糖果39块，如果姐姐给妹妹7块，就比妹妹少3块。那么姐姐和妹妹原来各有糖果多少块？‎ 3， 4， 5， 6， ‎3，两笼兔子共16只，若甲笼再放入4只，乙笼取出2只，这时两笼兔子只数就同样多。甲、乙两笼原来各有兔子多少只？‎ 例题4  把一条100米长的绳子剪成三段，要求第二段比第一段多16米，第三段比第一段少18米。三段绳子各长多少米？思路导航：用线段图来表示题意。‎ 可以这样想：把第一段绳子的长度当作标准，假设第二、第三段绳子都和第一段同样长，那么总长就变为100－16＋18=102米。第一段绳子长：102÷3=34米第二段绳子长：34+16=50米第三段绳子长：34－18=16米 练  习  四 1， 某工厂第一、二、三车间共有工人280人，第一车间比第二车间多10人，第二车间比第三车间多15人。三个车间各有工人多少人？‎ 2， 3， 1， ‎2，某工厂将857元奖金分给有创造发明的三名优秀工人，第一名比第二名多得250元，第二名比第三名多得125元。三名优秀工人各得多少元？‎ 2， 3， 4， 5， 6， 7， ‎3，小明期终考试的语文、数学和英语的平均分是95分，数学比语文多6分，英语比语文多9分。小明期终考试三门功课各多少分？‎ 例题5  四个人年龄之和是88岁，最小的3岁，他与最大的年龄之和比另外两个人年龄之和大8岁。最大的年龄是多少岁？思路导航：我们可以这样思考，将最大、最小两个人年龄的和与另外两人年龄和分别看作大数与小数，根据四个人的年龄和是88岁，年龄差是8岁，即可求出大数与小数。大数：（88+8）÷2=48岁最大的年龄：48－3=45岁 ‎ 练  习  五 1， 小军一家四口年龄之和是129岁，小军7岁，妈妈30岁，小军与爷爷年龄这和比他父母年龄之和大5岁。爷爷和爸爸的年龄各是多少岁？‎ 1， 2， 3， 4， ‎2，某校四个年龄共有438名学生，其中一年级119人，四年级101人，一、二年级的总人数比三、四年级的总人数多52人。二、三年级各有多少人？‎ 5， 6， 7， ‎3，某校四个年级共有138名学生参加数学竞赛，其中一、二年级共70名，一、三年级共65名，二、三年级共59名。四年级有多少名？‎ ‎1‎ 已知两个数的和与两个数间的倍数关系，求这两个数分别是多少，像这样的应用题，通常叫做和倍问题。要想顺利地解答和倍应用题，最好的方法就是根据题意，画出线段图，使数量关系一目了然，从而正确列式解答。解答和倍应用题，关键是要找出两数的和以及与其对应的倍数和，从而先求出1倍数，再求出几倍数。数量关系可以这样表示：两数和÷（倍数＋1）=小数（1倍数）小数×倍数=大数（几倍数）两数和－小数=大数 ‎ ‎ 和倍问题 例题1  学校将360本图书分给二、三两个年级，已知三年级所分得的本数是二年级的2倍，问二、三两个年级各分得多少本图书？思路导航：将二年级所得图书的本数看作1倍数，则三年级所得本数是这样的2倍。如图所示：‎ 由图可知，二、三年级所得图书本数的和360本相当于二年级的（1＋2）倍，则二年级所得图书本数的360÷（1＋2）=120本，三年级为120×2=240本。‎ ‎01‎ 小试牛刀 ‎1，小红和小明共有压岁钱800元，小红的钱数是小明的3倍。小红和小明各有压岁钱多少元？2，学校将360本图书分给二、三年级，已知三年级所得本数比二年级的2倍还多60本。二、三年级各得图书多少本？3，甲桶有油25千克，乙桶有油17千克，乙桶倒入多少千克油给甲桶后，甲桶油是乙桶的5倍？‎ 例题2  小宁有圆珠笔芯30枝，小青有圆珠笔芯15枝，问小青给小宁多少枝后，小宁的圆珠笔芯枝数是小青的8倍？思路导航：我们把变化后小青的圆珠笔芯枝数看作1倍数，那么小宁与小青圆珠笔芯的枝数和相当于变化后小青枝数的9倍，所以变化后小青的枝数为（30＋15）÷（1＋8）=5枝，再用15－5=10枝，则表示小青给小宁的枝数。‎ ‎02‎ 小试牛刀 ‎1，红红有邮票80张，佳佳有邮票60张，要使红红的邮票张数是佳佳的4倍，那么佳佳必须给红红多少张邮票？2，甲水池有水69吨，乙水池有水36吨，如果甲水池中的水以每分钟2吨的速度流入乙水池，那么多少分钟后，乙水池的水是甲水池的2倍？3，甲书架有图书18本，乙书架有图书8本，班图书管理员又买来图书16本，怎样分配才能使甲书架图书的本数是乙书架的2倍？‎ 例题3‎ ‎  被除数与除数的和为320，商是7，被除数和除数各是多少？思路导航：由商是7可知，被除数是除数的7倍，把除数看作1份数，被除数就有这样的7份，一共7＋1=8份。除数：320÷8=40被除数：40×7=280‎ ‎03‎ 小试牛刀 ‎1，被除数和除数和为120，商是7，被除数和除数各是多少？2，被除数、除数、商的和为79，商是4，被除数、除数各是多少？3，两个整数相除商是21，余数为1，已知被除数、除数、商、余数的和一共是441。被除数、除数各是多少？‎ 例题4  两数相除商为17余6，被除数、除数、商和余数的和是479。被除数和除数分别为多少？思路导航：被除数、除数、商和余数的和是479，减去商17和余数6，得到被除数与除数的和为479－17－6=456；又因为被除数比除数的17倍多6，所以456－6=450就相当于除数的（17＋1）倍，因此除数为450÷（17＋1）=25，被除数为25×17＋6=431。‎ ‎04‎ 小试牛刀 ‎1，两个整数相除商14余2，被除数、除数、商和余数的和是243，被除数比除数大多少？2，在一个减法算式里，被减数、减数与差的和等于240，而减数是差的5倍。差是多少？3，学校买来83本书，其中科技书是故事书的2倍，故事书比文艺书多5本，这三种书各多少本？‎ 例题5  两个数之和是792，其中一个数的最后一位数数字是0，如果把0去掉，就与另一个数相同。这两个数分别是多少？思路导航：把一个数的最后一位数字0去掉，就与另一个数相同，说明这两个数中大数是小数的10倍。又已知两个数之和是792，那我们就可以求出这两个数分别是多少了。小数：792÷（10＋1）=72大数：72×10=720‎ ‎05‎ 小试牛刀 ‎1，两个数之和是253，其中一个数的最后一位数字是0，如果把0去掉，就与另一个数相同。这两个数分别是多少？2，师徒两人加工一批零件共693个，师傅加工零件个数的末位数字是0，如果去掉这个0，加工的个数就与徒弟一样多。师徒二人分别加工零件多少个？3，甲、乙两数的和是209，甲数缩小10倍就和乙数同样大，甲、乙两数分别是多少？‎ 三年级数学思维训练：差倍问题 ‎1‎ 专题简析：‎ 前面我们已经初步掌握了“和倍问题”的特征和解题方法。如果知道了两个数的差与两个数间的倍数关系，要求两个数各是多少，这一类题，我们则把它称为“差倍问题”。小朋友，你们有没有想到用解答和倍问题的类似方法解答差倍问题呢？解答差倍问题与解答和倍问题相类似，要先找出差所对应的倍数，先求1倍数，再求出几倍数。此外，还要充分利用线段图帮助分析数量关系。用关系式可以这样表示：两数差÷（倍数－1）=较小的数（1倍数）较小的数×倍数=较大的数（几倍数）‎ ‎ ‎ 差倍问题（一）‎ 例题1  小明到市场去买水果，他买的苹果个数是梨的3倍，苹果比梨多18个。小明买苹果和梨各多少个？思路导航：将梨的个数看作1倍数，则苹果的个数是这样的3倍。如下图：‎ 从线段图上可以看出，苹果的个数比梨多了3－1=2倍，梨的2倍是18个，所以梨有18÷2=9个，苹果有：9×3=27个。‎ ‎01‎ 小试牛刀 1， 学校合唱组，女同学人数是男同学的4倍，女同学比男同学多42人。合唱组有男、女同学各多少人？‎ 2， 一件皮衣价钱是一件羽绒服价钱的5倍，又已知一件皮衣比一件羽绒服贵960元。皮衣与羽绒服各多少元？‎ 3， ‎，甲筐苹果是乙筐苹果的3倍，如果从甲筐取出60千克放入乙筐，那么两筐苹果重量就相等。两筐原来各有苹果多少千克？‎ 例题2  被除数比除数大252，商是7，被除数、除数各是多少？思路导航：根据“商是7”可知，被除数是除数的7倍，把除数看作1倍数，被除数就是这样的7份，比除数多6份。所以除数是：252÷（7－1）=42被除数是：42＋252=294‎ ‎02‎ 小试牛刀 ‎1，被除数比除数大168，商是22，被除数、除数各是多少？2，除数比被除数小212，商是5，被除数、除数各是多少？3，被除数比商大144，除数是7，被除数、商各是多少？‎ 例题3  水果店有两筐橘子，第一筐橘子的重量是第二筐的5倍，如果从第一筐中取出300个放入第二筐，那么第一筐橘子还比第二筐多60个。原来两筐橘子各有多少个？思路导航：根据“如果从第一筐中取出300个放入第二筐，那么第一筐橘子还比第二筐多60个”，说明原来第一筐比第二筐橘子多300×2＋60=660个。把第二筐的橘子重量看作1倍数，第一筐橘子是这样的5倍，比第二筐多4倍，第二筐橘子的4倍正好是660个，所以第二筐原有橘子：660÷4=165个，第一筐橘子原来有：165×5=825个。‎ ‎03‎ 小试牛刀 1， 同学们捐助残，六年级捐款钱数是三年级的3倍。如果从六年级捐款钱数中取出160元放入三年级，那么六年级捐款的钱数还比三年级多40元。两个年级分别捐款多少元？‎ 2， ‎，人民公园的杜鹃花盆数是长春园的4倍，如果从人民公园搬出188盆杜鹃花放入长春园，则人民公园的杜鹃花盆数就比长春园的少25盆。原来两个公园各有杜鹃花多少盆？‎ 3， ‎3，两堆煤重量相等，现从甲堆中运走24吨到乙堆，而乙堆煤中又运入8吨，这时乙堆煤的重量正好是甲堆煤重量的3倍。问两堆煤原来各有多少吨？‎ 例题4  甲、乙两个数，如果甲数加上280就等于乙数，如果乙数加上320就等于甲数的3倍。两个数各是多少？思路导航：根据题意，画出线段图：‎ ‎“甲数加上280就等于乙数”，说明乙数比甲数大280；如果乙数再加上320，甲、乙就相差320+280=600，把甲数看作1倍数，从图上可以看出，600就相当于甲数的3－1=2倍。所以，甲数为600÷2=300，乙数为300＋280=580。‎ ‎04‎ 小试牛刀 ‎1，甲、乙两人的存款相等，甲取出60元，乙存入20元后，乙的存款是甲的3倍。甲、乙两人原有存款各多少元？2，小明和小华的连环画本数相等，若小明借给小华6本，小华的本数是小明的4倍。原来两人各有连环画多少本？3，两筐千克数相同的苹果，甲筐卖出7千克，乙筐卖出19千克后，甲筐余下的苹果是乙筐的3倍。两筐苹果原来各有多少千克？‎ 例题5  两个书架所存书的本数相等，如果从第一个书架里取出200本书，而第二个书架再放入40本书，那么第二个书架的本数是第一个书架的3倍。问两个书架原来各存书多少本？思路导航：根据题意，画出线段图。‎ 从线段图上可以看出，第一个书架取出200本，第二个书架放进40本书后，两个书架就相差200+40=240本，把变化后的第一个书架看作1倍数，两个书架相差的240本就相当于变化后第一个书架的（3－1）倍。所以，变化后第一个书架有书： ‎ ‎（200＋40）÷（3－1）=120本两个书架原来各有：120＋200=320本。‎ ‎05‎ 小试牛刀 ‎1，两个仓库所存粮食重量相等，如果从第一个仓库里取出2000千克，而第二个仓库再存入400千克，那么第二个仓库的粮食重量就是第一个仓库的7倍。两个仓库原来各存粮食多少千克？2，小红和小明的铅笔枝数相等，如果奶奶再给小红16枝铅笔，给小明2枝铅笔，那么小红的铅笔枝数就是小明的3倍。原来小红和小明各有铅笔多少枝？3，商店有数量相等的英语本和算术本，英语本卖出160本，算术本卖出420本后，余下的英语本数是算术本的3倍。两种本子原来各有多少本？‎ ‎【已更新】三年级数学思维训练：差倍问题（二）‎ 先哥微课堂 1月21日 如果你尚未关注本公众号，可通过以下三种方式关注本公众号：‎ ‎1.点上面蓝色“先哥微课堂”字关注本公众号。       ‎ ‎2.微信搜索公众号“先哥微课堂”添加关注本公众号。      ‎ ‎3.长按下面的二维码3秒关注本公众号。‎ ‎    ‎ 专题简析：‎ 有些差倍问题比较复杂，不能直接利用公式进行解答，这时需要我们小朋友仔细审题，尤其注意一些隐含条件，同时借助线段图帮助理解题意，从而找到解题方法。较复杂的差倍应用题，数量关系比较隐蔽。先依题意画出线段图，数量关系就会比较清晰地展现出来，然后借助线段图找出两个数的差以及所对应的倍数，再利用公式进行解答。‎ ‎ ‎ 差倍问题（二）‎ 例题1  有两袋玉米，大袋比小袋多56千克，如果将小袋的玉米吃掉4千克，这时大袋的玉米重量是小袋的4倍。两袋玉米原来各重量多少千克？‎ 思路导航：根据题意，画出线段图。‎ 从图上可以看出，小袋玉为吃掉4千克后，大袋里的玉米就比小袋现有玉米重4+56=60千克；又根据“这时大袋的玉米重量是小袋的4倍”，可知把小袋现有的玉米重量看作1倍数，大袋比小袋多的60千克正好相当于现有小袋的4－1=3倍，所以小袋现有玉米60÷3=20千克，原有重量20+4=24千克，大袋原有20×4=80千克。‎ ‎01‎ 小试牛刀 ‎1，有两箱玩具，第一盒比第二盒多60只。如果从第二盒中取出3只，这时第一盒的只数是第二盒的8倍。求两箱玩具原来各有多少只？2，一个书架上放着一些书，第二层比第一层多12本。如果从第一层中拿走6本，这时第二层的本数是第一层的4倍。求第一、第二层原来各有多少本书？3，甲、乙两桶油各有油若干千克，甲桶的油比乙桶少20千克，如果从甲桶倒出5千克放入5千克，这时乙桶内油的重量是甲桶的4倍。甲、乙两桶原来各有油多少千克？‎ 例题2  有甲、乙两桶色拉油，如果向甲桶中倒入8千克，则两桶色拉油就一样重；如果向乙桶中倒入12千克，乙桶的色拉油就是甲桶的5倍。甲、乙两桶原来各有色拉油多少千克？‎ 思路导航：根据题意，画出线段图。‎ 从线段图上可以看出：如果向甲桶倒入8千克，两桶油重量相等，说明乙桶油比甲桶油多8千克；如果向乙桶倒入12千克，乙桶油就比甲桶油多8+12=20千克，与20千克相对应的倍数差是5－1=4倍。所以，甲桶原有：（8+12）÷（5－1）=5千克，乙桶原有5+8=13千克。‎ ‎02‎ 小试牛刀 1， 有甲、乙两桶水，如果向甲桶中倒入10千克水，两桶水就一样多；如果向乙桶中倒入4千克水，乙桶的水就是甲桶的3倍。原来甲、乙两桶各有多少千克水？‎ 2， 3， 4， 5， 6， ‎2，三（1）班同学参加英语比赛，如果男生少去1人，男、女参赛人数相等；如果女生少去1人，男生参赛人数是女生的2倍。三（1）班参加英语比赛的男、女生各几人？‎ 7， 8， 9， 10， 11， ‎3，小敏和小文每人都有一些玻璃球，如果小敏给小文3粒，两人的玻璃球数就一样多；如果小文给小敏1粒，小敏的玻璃球数就是小文的5倍。小敏、小文原有玻璃球各几粒？‎ 例题3  甲的钱数是乙的3倍，甲买一套180元的《百科大全》，乙买一套30元的故事书后，两人余下的钱一样多。甲原来有多少钱？‎ 思路导航：根据题意，画出线段图。‎ 把乙原有的钱看作1份，甲原有的钱不是3份；甲买书用去180元，乙买书用去30元，甲比乙多用去180－30=150元。从图上可以看出，这多出的150元正好相当于乙原有钱数的3－1=2倍，所以乙原有钱：150÷2=75元，甲原有钱75×3=225元。‎ ‎03‎ 小试牛刀 1， 甲的钱数是乙的4倍，甲买了一只30元的书包，乙买了一枝6元的钢笔后，两人余下的钱一样多。甲原来有多少钱？‎ 2， 3， 4， 5， ‎2，丹丹的钱数是小敏的5倍，丹丹买了一套115元的衣服，小敏买了一双15元的鞋子后，两人余下的钱一样多。丹丹原来有多少钱？‎ 6， 7， 8， 9， 云云的钱是小月的4倍，云云买了一套水彩笔用了19元钱，小月买了一块1元钱的橡皮后，两人剩下的钱一样多。云云原来有多少钱？‎ 例题4  学校里白粉笔的盒数是彩色粉笔的4倍，如果白粉笔和彩色粉笔各购进12盒，那么白粉笔的盒数是彩色粉笔的3倍。原来白粉笔和彩色粉笔各有多少盒？‎ 思路导航：根据题意，如果彩色粉笔购进12盒，而白粉笔购进12×4=48盒，那么现在白粉笔的盒数仍是彩色粉笔的4倍，可见48－12=36盒就是彩色粉笔现有盒数的4－3=1倍，所以彩色粉笔现有36÷1=36盒，原来有36－12=24盒，白粉笔原有24×4=96盒。‎ ‎04‎ 小试牛刀 ‎1，有甲、乙两筐苹果，甲筐苹果的千克数是乙筐的3倍，如果两筐苹果各增加8千克，那么甲筐苹果的千克数就是乙筐的2倍。甲、乙两筐原来各有多少千克苹果？2，小明和聪聪各有一些彩色笔，小明彩色笔的枝数是聪聪的5倍。如果每人再买4枝彩色笔，那么小明的枝数就是聪聪的4倍。小明和聪聪原来各有彩色笔多少枝？3，有甲、乙两桶油，甲桶油的重量是乙桶油的5倍。如果每桶分别倒入8千克的油，那么甲桶油的重量是乙桶油的3倍。甲、乙两桶原来各有多少千克油？‎ 例题5  天天小学买来了一批篮球和足球，篮球的个数比足球的4倍多5个，篮球比足球多26个。篮球和足球各多少个？‎ 思路导航：根据题意，画出线段图。‎ 从图上可以看出，如果把足球的个数看作1倍数，那么篮球减少5个就是足球个数的4倍，所以足球有（26－5）÷（4－1）=7个，篮球有7×4＋5=33个。‎ ‎05‎ 小试牛刀 1， 商店里有一些红皮球和白皮球，红皮球的个数比白皮球的3倍多2个，红皮球比白皮球多24个。红、白皮球各有多少个？‎ 2， 3， 4， 5， ‎2，有两袋面粉，甲袋面粉比乙袋面粉的5倍多12千克，乙袋比甲袋少132千克。甲、乙两袋面粉各多少千克？‎ 6， 7， 8， 1， ‎3，图书室里有一些故事书和连环画，故事书的本数比连环画的4倍少8本，故事书比连环画多28本。图书室里有故事书和连环画各多少本？‎ 三年级数学思维训练：植树问题 ‎1‎ 专题简析：‎ 爸爸给晶晶出了一道题：“小朋友在路的一边植树，先植一棵树，以后每隔3米植一棵，已经植了9棵，问第一棵和第九棵树相距多少米？”晶晶一看，随口答道：“27米。”小朋友，晶晶答得对吗？这一类应用题我们通常称为“植树问题”。解答这类问题的关键是要弄清总距离、间隔长和棵树三者之间的关系。解答植树问题要考虑植树的方式，一般在不封闭的线路上植树，棵数=总距离÷间隔长＋1；在封闭的线路上植树，棵数=总距离÷间隔长。另外，生活中还有一些问题，可以用植树问题的方法来解答，比如锯木头、爬楼梯问题等等，这里解题的关键是要将题目中的条件与问题与植树问题中的总距离、间隔长、棵数对应起来。‎ ‎ ‎ 植树问题 例题1  小朋友们植树，先植一棵树，以后每隔3米植一棵，已经植了9棵，第一棵和第九棵相距多少米？思路导航：要得出正确的结果，我们可以画出如下的示意图：‎ 根据“已经植了9棵”，从图中我们可以看出，第一棵树和第九棵树之间的间隔是9－1=8个，每个间隔是3米，所以第一棵和第九棵相距3×8=24米。‎ ‎01‎ 小试牛刀 1， 在路的一侧插彩旗，每隔5米插一面，从起点到终点共插了10面。这条道路有多长？‎ ‎2，在学校的走廊两边，每隔4米放一盆菊花，从起点到终点一共放了18盆。这条走廊长多少米？3，在一条20米长的绳子上挂气球，从一端起，每隔5米挂一个气球，一共可以挂多少个气球？‎ 例题2  在一条长40米的大路两侧栽树，从起点到终点一共栽了22棵。已知相邻两棵树之间的距离都相等，问相邻两棵树之间的距离是多少米？思路导航：根据“在路的两侧共栽22棵树”这个条件，我们可先求出一侧栽了22÷2=11棵树，那么从第1棵树到第11棵树之间的间隔是11－1=10个。40米长的大路平均分成10段，每段是40÷10=4米。‎ ‎02‎ 小试牛刀 1， 在一条长32米的公路一侧插彩旗，从起点到终点共插了5面，相邻两面旗之间距离相等，相邻两面旗之间相距多少米？‎ 2， 在公园一条长25米的路的两侧放椅子，从起点到终点共放了12把椅子，相邻两把椅子距离相等。相邻两把椅子之间相距多少米？‎ ‎3，有一根木头，要锯成8段，每锯开一段需要2分钟，全部锯完需要多少分钟？‎ 例题3  把一根钢管锯成小段，一共花了28分钟。已知每锯开一段需要4分钟，这根钢管被锯成了多少段？要求钢管被锯的段数，必须首先求出钢管被锯开几处。‎ 思路导航：从图中我们可以看出钢管有28÷4=7处被锯开，因而锯开的段数有7＋1=8段。‎ ‎03‎ 小试牛刀 1， 一根木料，要锯成4段，每锯开一处要5分钟，全部锯完要多少分钟.‎ 2， 一根圆木锯成2米长的小段，一共花了15分钟。已知每锯下一段要3分钟，这根圆木长多少米？‎ ‎3，小明爬楼梯，每上一层要走12级台阶，一级台阶需走2秒。小明从一楼到四楼共要走多少时间？‎ 例题4  在一个周长是48米的池塘周围种树，每隔6米种一棵树，一共种了多少棵？思路导航：无论这个池塘是什么形状，种的树都可围成一个封闭路线，有下面几种情况可看出，封闭线路中有几个间隔，就能种几棵树。‎ 已知池塘周长为48米，间隔长是6米，所以要种48÷6=8棵。‎ ‎04‎ 小试牛刀 1， 在一个周长是42米的长方形花园周围，每隔2米放一盆花，一共可放多少盆花？‎ 2， 要在一个水池周围种树，已知这个水池周长为245米，计划要栽49棵树，相邻两树之间距离相等。相邻两树之间相距多少米？‎ ‎3，在一个边长为12米的正方形四周围篱笆，每隔4米打1根木桩，一共要准备多少根木桩？‎ 例题5  甲、乙两人比赛爬楼梯，甲跑到5楼时，乙恰好跑到3楼。照这样计划，甲跑到17楼时，乙跑到多少层？思路导航：解答爬楼梯问题，不能以楼层进行计算，而要用楼梯段数进行计算。因为第一层楼是不用爬的，（楼层数－1）才是要走的楼梯段数。根据题意“甲跑到5楼时，乙恰好跑到3楼”，实际是说甲跑（5－1）段楼梯，与乙跑（3－1）段楼梯时间相同，照这样计算，甲跑到17楼，也就是跑了（17－1）段楼梯，应是跑（5－1）段楼梯所用时间的4倍，在同一时间时乙跑的楼梯段数也是他跑（3－1）段楼梯的4倍，也就是这时他跑了8段楼梯，即他跑到了第8＋1=9层楼。‎ 三年级数学思维训练：应用题 ‎1‎ 专题简析：‎ 应用题是小学数学中非常重要的一部分内容，它需要我们小朋友用学到的数学知识来解决生产、生活中的一些实际问题。学好应用题的关键在于认真分析题意，掌握数量关系，找到问题的突破口。在分析应用题的数量关系时，我们可以从条件出发，逐步推出所求的问题；也可以从问题出发，找到必须的两个条件。在实际解答时，我们可以根据题目中的数量关系，灵活运用这两种方法。有时，借助线段图来分析应用题的数量关系，解答就更容易了。‎ ‎ ‎ 应用题（一）‎ 例题1  学校里有排球24只，足球的只数比排球的2倍少5只，学校有排球、足球共多少只？思路导航：根据题意画出线段图 从上图可以看出，把24只排球看作1倍数，足球的只数比这样的2倍还少5只，用24×2－5=43（只）可以求出足球的只数，再用43＋24=67只可以求出两种球的总只数。‎ ‎01‎ 小试牛刀 1， 小红每分钟跳绳25下，小军每分钟跳的下数比小红的3倍少16下，小军每分钟比小红多跳几下？‎ 2， ‎2，王奶奶家养鸡12只，养鹅的只数比鸡的只数的4倍还多7只。王奶奶家共养鸡、鹅多少只？‎ ‎3，少先队员种柳树30棵，种的杨树的棵数比柳树棵数的3倍多14棵。少先队员种的杨树、柳树共多少棵？‎ 例题2  人民广场花圃中有180盆郁金香，比月季花盆数的3倍少15盆。月季花有多少盆？‎ 思路导航： 从上图可以看出，把月季花的盆数看作1倍数，郁金香的盆数是这样的3倍少15盆。如果郁金香再增加15盆，就正好是月季花盆数的3倍。因此用（180＋15）÷3=65（盆）就可求出月季花的盆数。‎ ‎02‎ 小试牛刀 1， 小明的父亲每月工资1000元，比小明母亲每月工资的2倍少200元。小明母亲每月工资多少元？‎ 2， 饲养场养母鸭400只，比公鸭只数的7倍还多36只。饲养场养公鸭多少只？‎ ‎3，水果店卖出9筐水果，平均每筐重45千克。卖出水果的千克数比剩下的3倍还多27千克，还剩多少千克水果？‎ 例题3  小林家养了一些鸡，黄鸡比黑鸡多13只，白鸡比黄鸡多12只，白鸡的只数正好是黑鸡的2倍。白鸡、黄鸡、黑鸡各多少只？‎ 思路导航： ‎ 根据“黄鸡比黑鸡多13只，白鸡比黄鸡多12只”，从线段图上我们可以看出白鸡比黑鸡多13＋12=25只，这相当于黑鸡的2－1=1倍，这样也就求出黑鸡的只数为25÷1=25只，黄鸡的只数是25＋13=38只，白鸡的只数是25×2=50只。‎ ‎03‎ 小试牛刀 1， 商店里有红、白、蓝三种围巾，其中红围巾比白围巾多12条，蓝围巾比红围巾多20条，蓝围巾的条数正好是白围巾的5倍。红围巾、白围巾、蓝围巾各多少条？‎ 2， 有甲、乙、丙三筐苹果，甲筐比乙筐多12只苹果，丙筐比甲筐多15只苹果，丙筐苹果个数是乙筐的4倍。甲、乙、丙筐各有多少只苹果？‎ ‎3，男女学生参加小组交流会，如果少去1名女生，男女生人数相等；如果少去一名男生，女生人数是男生的2倍。参加交流会的男女生各多少人？‎ 例题4‎ ‎  用一批纸装订同样大小的练习本，如果每本16页，可装订400本。如果每本20页，可以少装订多少本？思路导航：根据“如果每本16页，可装订400本”，可得这批纸的总页数16×400=6400页；再用总页数6400÷20=320本求出如果每本20页可装订的本数，400－320=80本则表示少装订的本数。‎ ‎04‎ 小试牛刀 1， 水果市场要将一些水果装箱，如果每箱10千克，可装30箱。如果每箱15千克，可少装多少箱？‎ ‎2，服装厂有一些布料加工窗帘，如果把窗帘做成3米长，可做140幅。如果每幅窗帘做成2米长，则可多做多少幅？‎ ‎3，同一批纸装订同样大小的练习本，如果每本16页，可装订400本。如果每本多装订9页，则少装订多少本？‎ 例题5‎ ‎  李师傅原计划6小时加工零件480个，实际2小时加工192个。照这样的效率，可以提前几小时完成？思路导航：根据“实际2小时加工192个”，可以求出李师傅的实际工作效率为192÷2=96（个/小时），再用要加工的零件总数除以实际工作效率，即480÷96=5小时，求出实际完成的时间。6－5=1小时，则表示提前完成的时间。‎ ‎05‎ 小试牛刀 1， 王奶奶计划10小时做纸盒400个，实际3小时已加工150个。照这样的效率，可以提前几小时完成？‎ 2， 暑假中，小宁30天共要写大字600个，实际12天已写大字360个。照这样的速度，小宁可以提前几天写完同样多的字？‎ ‎3，自行车制造厂四月份（30天）共生产自行车3600辆，五月份改进技术后9天已生产自行车1350辆。照这样的效率，可以提前几天完成四月份的任务？‎ ‎ ‎ 应用题（二）‎ 例题1  一列火车早上5时从甲地开往乙地，按原计划每小时行驶120千米，下午3时到达乙地，但实际到达时间是下午5时整，晚点2小时。问火车实际每小时行驶多少千米？思路导航：由“这列火车早上5时出发，计划下午3时到达”可知，这列火车原计划行驶12＋3－5=10小时，用原计划每小时行驶120千米×计划行驶的10小时，便可得到甲地到乙地的距离为120×10=1200千米；火车晚点2小时，说明火车实际行驶了10＋2=12小时，用1200÷12=100千米就可得到火车实际每小时行的千米数。‎ ‎01‎ 小试牛刀 1， 一辆汽车早上8点从甲地开往乙地，按原计划每小时行驶60千米，下午4时到达乙地。但实际晚点2小时到达，这辆汽车实际每小时行驶多少千米？‎ 1， 一列火车早上6时从甲城开往乙城，计划每小时行驶100千米，下午6时到达乙城。但实际到达时间是下午4时，提前2小时。问火车实际每小时行驶多少千米？‎ ‎3，王叔叔驾驶一辆摩托车，上午11时从城开到城西，计划每小时行驶60千米，下午2时到达城西，实际到达时间是下午3时，晚到1小时。问实际每小时比计划少行多少千米？‎ 例题2  小宁、小红、小佳去买铅笔，小宁买了7枝，小红买了5枝，小佳没有买。回家后，三个人平均分铅笔，小佳拿出8角钱，小佳应给宁多少钱？给小红多少钱？思路导航：小宁和小红一共买了7＋5=12枝铅笔，三个人平均分，每人应得12÷3=4枝，所以小佳拿出的8角钱就相当于4枝铅笔的价钱，那么每枝铅笔的价钱应是8÷4=2角。小佳应给小宁2×（7－4）=6角钱，应给小红2×（5－4）=2角钱。‎ ‎02‎ 小试牛刀 1， 三个好朋友去买饮料，小亮了5瓶，小华买了4瓶，阳阳没有买。到家后，三个人平均喝完饮料，阳阳拿出6元钱，他应给小亮多少钱？给小华多少钱？‎ 2， 甲、乙、丙3人一起买了6个面包分着吃，甲、乙各拿出3个面包的钱，丙没有带钱。那么吃完后，丙应拿出4元8角钱，他应分别给甲、乙多少钱？‎ ‎3，张、王、李三家合用一个炉灶，他们烧的柴同样多，张家出了4担柴，李家出了5担柴，王家因无柴付18元。张、李家各得多少钱？‎ 例题3  用一个杯子向空瓶里倒牛奶，如果倒进去2杯牛奶，连瓶共重450克；如果倒进去5杯牛奶，连瓶共重750克。一杯牛奶和一个空瓶各重多少克？思路导航：根据题目的条件，我们可以写出两个关系式：2杯牛奶重量＋1个空瓶重量=450克  （1）5杯牛奶重量＋1个空瓶重量=750克 ‎ ‎ （2）比较（1）、（2）两个式子，可发现用（2）－（1）可消去空瓶重量，并可得到5－2=3瓶牛奶重量是750－450=300克，那么1瓶牛奶重量是300÷3=100克，然后可求出空瓶重量是450－100×2=250克。‎ ‎03‎ 小试牛刀 1， 有12筐苹果，它们重量相等，我们把它们装入一个大箱子里，如果装进2筐苹果，连箱共重量220千克；如果装进5筐苹果，连箱共重520千克。1筐苹果和大箱子各重多少千克？‎ 2， 有一个木桶向一个水缸中倒水，如果倒进4桶水，连缸共重240千克；如果倒进7桶水，连缸共重390千克。一桶水和一个水缸各重多少千克？‎ ‎3，有一瓶水，向几个相同的杯子里注水，如果注满3杯水，连瓶重550克；如果注满6杯水，连瓶共重250克。一杯水多重？‎ 例题4  一共有红、黄、绿三种颜色的珠子120粒。如果把红色珠子分放在9个盒子里，把黄色珠子分放在6个盒子里，把绿色珠子分放在5个盒子里，那么每个盒子里的珠子粒数相等。三种颜色的珠子各多少粒？思路导航：把120粒珠子分放到盒子里以后，每个盒子里的珠子粒数相等，那么就可以120÷（6＋9＋5）=6粒，求出每个盒子里珠子的粒数，然后再求三种颜色的珠子各几粒。红色珠子：6×9=54粒；黄色珠子：6×6=36粒；绿色珠子：6×5=30粒。‎ ‎04‎ 小试牛刀 1， 一共有苹果、梨、橘子共105个，如果把苹果分放到4个盘中，把梨分放到5个盘中，把橘子分放到6个盘中，那么每个盘子的水果个数相等。三种水果各多少个？‎ 2， 一共有白兔、灰兔、黑兔共250只，如果把白兔分放到5个笼中，把灰兔分放到11个笼中，把黑兔分放到9个笼中，这样每个笼中的兔子的只数相等。三种兔子各多少只？‎ ‎3，共有科技书、文艺书和故事书共360本，若把科技书分放到2个书架上，把文艺书分放到3个书架上，把故事书分放到4个书架上，则每个书架上的本数相等。三种书各有多少本？‎ 例题5  在6个筐里放着同样多的鸡蛋，如果从每个筐里拿出50个鸡蛋，则6个筐里剩下的鸡蛋个数的总和等于原来两个筐里鸡蛋个数的总和。原来每个筐里有鸡蛋多少个？思路导航：根据“6个筐里剩下的鸡蛋个数的总和等于原来5个筐里鸡蛋个数的总和”，说明6个筐里取出的鸡蛋个数的总和等于原来（6－2）=4个筐里鸡蛋的总和，用取出的50×6=300个鸡蛋除以4就可求出原来每个筐里的鸡蛋个数：300÷4=75个。‎ ‎05‎ 小试牛刀 ‎1，在6个纸箱中放着同样多的苹果。如果从每个纸箱里拿出50个苹果，则6个箱里剩下的苹果个数的总和等于原来2个箱子的苹果个数的总和。原来每个箱里有多少个苹果？2，某商店有5箱皮球，如果从每箱里取出15个，那么5个箱里剩下皮球的个数正好等于原来2箱皮球的个数。原来每箱装了多少个皮球？3，有3个水桶，如果从每桶中倒出4千克水，那么3桶里剩下的水的重量正好等于原来1桶的重量。原来每桶装多少千克水？‎ 三年级数学思维训练：配对求和 ‎1‎ 专题简析：‎ 被人称为“数学王子”的高斯在年仅8岁时，就以一种非常巧妙的方法又快又好地算出了1＋2＋3＋4＋…＋99＋100的结果。小高斯是用什么办法算得这么快的呢？原来，他用了一种简便的方法：先配对再求和。数列的第一项叫首项，最后一项叫末项。如果一个数列从第二项起，每一项与前一项的差是一个不变的数，这样的数列叫做等差数列，这个不变的数则称为这个数列的公差。计算等差数列的和，可以用以下关系式：等差数列的和=（首项＋末项）×项数÷2末项=首项＋公差×（项数－1）项数=（末项－首项）÷公差＋1‎ ‎ ‎ 配对求和 例题1  你有好办法算一算吗？       1＋2＋3＋4＋5＋6＋7＋8＋9＋10=（    ）思路导航：1、2、3、4、5、6、7、8、9、10共10个数，我们可以把10个数分成5组：1＋10，2＋9，3＋8，……，每组两个数的和是11，它们的和就有5个11即11×5=55。‎ ‎01‎ 小试牛刀 ‎1，计算：1＋2＋3＋4＋…＋20；2，你能迅速算出结果吗？1＋2＋3＋4＋…＋100；3，想一想，该怎样计算方便？  21＋22＋23＋24＋…＋50。‎ 例题2‎ ‎  你能迅速算出下列算式的结果吗？       1＋2＋3＋4＋5＋6＋7＋8＋9=（   ）思路导航：1、2、3、4、5、6、7、8、9一共9个数，如果我们还像例1那样两个数组成一组，就有一个数多出来，那怎样做呢？我们可以这样想： ‎ ‎9个10是90，90是两组1加到9的和，它的一半是90÷2=45。当加数个数成单时，我们可以用第一个数与最后一个数相加，乘这组数的个数，再除以2，其实这种方法也适用于加数个数成双的求和。‎ ‎02‎ 小试牛刀 用简单方法迅速算出下面的题。1，1＋2＋3＋4＋…＋55；2，1＋2＋3＋4＋…＋99；3，56＋57＋58＋…＋76。‎ 例题3  计算：（1）32＋34＋36＋38＋40＋42（2）203＋207＋211＋215＋219思路导航：（1）32、34、36、38、40、42共6个数相加，后一个数与前一个数相差都是2，我们可以把它们分为3组，每组的和都是74，那么几个数的和就是3个74即74×3=222；（2）203＋207＋211＋215＋219共5个数相加，后一个数与前一个数相差都是4，我们也可以仿照例2的方法进行计算，用第一个数和最后一个数相加203＋219=422，乘上数的个数5，即422×5=2110，再除以2得到2110÷2=1055。‎ ‎03‎ 小试牛刀 计算：1，48＋50＋52＋54；2，128＋138＋148＋158＋168；3，72＋75＋78＋81＋84。‎ 例题4  计算：       993＋994＋995＋996＋997＋998＋999思路导航：这题求几个连续自然数的和，它们都接近于1000，我们可以看作7个1000相加，这样就多加了7＋6＋5＋4＋3＋2＋1，就用7000－（7＋6＋5＋4＋3＋2＋1）=6072。‎ ‎04‎ 小试牛刀 ‎1，计算：（1）97＋98＋99；（2）1997＋1998＋1999。2，你能迅速算出下题吗？9995＋9996＋9997＋9998＋9999‎ 例题5‎ ‎  计算： 1000―81―19―82―18―83―17―84―16―85―15―86―14―87―13―88―12―89―11思路导航：通过观察，我们可以发现每两个减数相加的和是100，我们可以把81和19，82和18，83和17，84和16，85和15，86和14，87和13，88和12，89和11这几组数先加起来，和为9个100即900，然后再从1000中减900得100。‎ ‎05‎ 小试牛刀 ‎1，计算：（1）1000―1―9―2―8―3―7―4―6―5―5―6―4―7―3―8―2―9―1（2）1000―71―29―72―28―73―27―74―26―75―25―76―24―77―23―78―22―79―212，计算：1000―91―1―92―2―93―3―94―4―95―5－96―6―97―7―98―8―99―9‎ 三年级数学思维训练：数学趣题 ‎1‎ 专题简析：‎ 在日常生活中，常有一些妙趣横生、带有智力测试性质的问题，如：3个小朋友同时唱一首歌要3分钟，100个小朋友同时唱这首歌要几分钟？类似这样的问题一般不需要较复杂的计算，也不能用常规方法来解决，而常常需要用小朋友的灵感、技巧和机智获得答案。‎ 对于趣味问题，首先要读懂题意，然后要经过充分的分析和思考，运用基础知识以及自己的聪明才智巧妙地解决。‎ 数学趣题 例题1  如果每人步行的速度相同，2个人一起从学校到儿童乐园要3小时，那么6个人一起从学校到儿童乐园要多少小时？‎ 思路导航：‎ ‎2个人一起从学校到儿童乐园要3小时，也就是1个人从学校到儿童乐园要3小时；6个人一起从学校到儿童乐园所用的时间与一个人所用的时间相等，所以6个人一起从学校到儿童乐园还是用3小时。‎ ‎01‎ 小试牛刀 ‎1，3个人同时唱3首歌用9分钟，9个人同时唱同样的3首歌用几分钟？‎ ‎2，5只猫5天能捉5只老鼠，照这样计算，要在100天里捉100只老鼠要多少只猫？‎ ‎3，6个人从甲地到乙地用4小时，如果每人的步行速度相同，那么3个人从甲地到乙地要用几小时？‎ 例题2  一条毛毛早由幼虫长成成虫，每天长大一倍，30天能长到20厘米。问长到5厘米时要用多少天？‎ 思路导航：‎ 毛毛虫每天长大一倍，说明第二天的身长是第一天身长的2倍。这条毛毛虫在第30天时，身长为20厘米，那么在第29天时，这条毛毛虫的身长为20÷2=10厘米；在第28天时，这条虫的身长为10÷2=5厘米。‎ ‎02‎ 小试牛刀 1， 有一个池塘中的睡莲，每天长大一倍，经过10天可以把整个池塘全部遮住。问睡莲要遮住半个池塘需要多少天？‎ 2， 一条小青虫由幼虫长成成虫，每天长大一倍，20天能长到36厘米。问长到9厘米时要用几天？‎ ‎3，一条毛毛虫由幼虫长成成虫，每天长大一倍，15天能长到4厘米。问要长到32厘米共要多少天？‎ 例题3  小猫要把15条鱼分成数量不相等的4堆，问最多的一堆中最多可放几条鱼？‎ 思路导航：‎ 小猫要把15条鱼分成数量各不相等的4堆，要让最多的一堆中小鱼条数尽量多，那么其余三堆小鱼的条数就要尽量少。所以，小猫可以在第一堆中放1条，在第二堆中放2条鱼，在第三堆中放3条鱼，这样第四堆就可放：‎ ‎15－（1＋2＋3）=9条。‎ ‎03‎ 小试牛刀 1， 小明要把20颗珠子分成数量不等的5堆，问最多的一堆中最多可放几颗珠子？‎ 2， 老师为共有18人的舞蹈队设计队形，要求分成人数不等的5队，问最多的一队最多可排几人？‎ ‎3，兔妈妈拿来1盘萝卜共25个，分给4只小兔，要使每只小兔分得的个数都不同。问分得最多的一只小兔至多分得几只？‎ 例题4  把100只桃子分装在7个篮子里，要求每个篮子里装的桃子的只数都带有6字。想一想，该怎样分？‎ 思路导航：‎ 因为6×6=36只，这样就可以在每个篮子里装6只桃，共装6个篮子，还有一个篮子里装100－36=64只桃。64这个数，正好也含有数字6，符号题目要求。‎ ‎04‎ 小试牛刀 1， 把100个鸡蛋分装在6个盒里，要求每个盒里装的鸡蛋的数目都带有6字，想想看，应该怎样分？‎ 2， 有人认为8是个吉祥数字，他们得到的东西的数量都要含有数字8。现在有200块糖要分给一些人，请你帮助设计一个吉祥的分糖方案。‎ ‎3，7只箱子分别放有1只、2只、4只、8只、16只、32只、64只苹果，现在要从这7只箱子里取出87只苹果，但每只箱子内的苹果要么全部取走，要么不取。你看该怎么取？‎ 例题5  舒舒和思思到书店去买书，两人都想买《动脑筋》这本书，但钱都不够。舒舒缺2元8角，思思缺1分钱，用两个人合起来的儿买一本，仍然不够。这本书多少钱？‎ 思路导航：‎ 思思买这本书缺1分钱，两个人合起来的钱买一本书仍然不够，这说明舒舒根本没有钱，所以这本书的价钱是2元8角。‎ ‎05‎ 小试牛刀 1， 小华和娟娟到商店买文具盒，两人看中同一个文具盒，但钱都不够。小华缺9元4角，娟娟缺1分，两人合起来买一个仍然不够。这个文具盒多少钱？‎ 2， 李华和张洁到商店买同一种练本，但发现钱都没带够，李华缺6角，张洁缺2分钱，但两人合起来买一本仍不够。这种本子一本多少钱？‎ ‎3，王阿姨和李阿姨到商场买电视机，两人都看中同一种电视机，但王阿姨缺600元，李阿姨缺900元，用两人带的钱合起来买这一台电视机正好。这台电视机多少钱？‎ 三年级数学思维训练：周期问题 ‎1‎ 专题简析：‎ 在日常生活中，有一些按照一定的规律不断重复的现象，如：人的十二生肖，一年有春夏秋冬四个季节，一个星期七天等等。像这样日常生活中常碰到的有一定周期的问题，我们称为简单周期问题。这类问题一般要利用余数的知识来解答。‎ 在研究这些简单周期问题时，我们首先要仔细审题，判断其不断重复出现的规律，也就是找出循环的固定数，然后利用除法算式求出余数，最后根据余数得出正确的结果。‎ 周期问题 例题1  小丁把同样大小的红、白、黑珠子按先2个红的、后1个白的、再3个黑的的规律排列（如下图），请你算一算，第32个珠子是什么颜色？‎ 分析：从上图可以看出，珠子是按“两红一白三黑”的规律重复排列，即6个珠子为一周期。32÷6=5（组）……2（个），32个珠子中含有5个周期多2个，所以第32个珠子就是重复5个周期后的第2个珠子，应为红色。‎ ‎01‎ 小试牛刀 ‎1，如图，算出第20个图形是什么？‎ ‎  ○△△□□□○△△□□□○△△……‎ ‎2，“数学趣味题数学趣味题……”依次重复排列，第2001个字是什么？‎ ‎3，把38面小三角旗按下图排列，其中有多少面白旗？‎ 例题2      2001年10月1日是星期一，问：10月25日是星期几？‎ 思路导航：我们知道，每星期有7天，也就是说以7天为一个周期不断地重复。从10月1日到10月25日共有25天，25÷7=3（星期）……4（天），说明25天中包括3个星期还多4天。所以10月25日是第4个星期的第四天，它与第一个星期的第四天相同，由于10月1日是星期一，从它开始，过25天就是星期四。‎ ‎02‎ 小试牛刀 ‎1，2001年5月3日是星期四，5月20日是星期几？‎ ‎2，2001年8月1日是星期三，8月28日是星期几？‎ ‎3，2001年6月1日是星期五，9月1日是星期几？‎ 例题3      100个3相乘，积的个位数字是几？‎ 思路导航：这道题我们只考虑积的个位数字的排列规律。1个3，积的个位是3；2个3相乘积的个位数字是9；3个3相乘积的个位数字是7；4个3相乘积的个位数字是1；5个3相乘积的个位数字是3……可以发现，积的个位数字分别以3、9、7、1不断重复出现，即每4个3积的个位数字为一周期。100÷4=25（个），因此100个3相乘积的个位数字是第25个周期中的最后一个，即是1。‎ ‎03‎ 小试牛刀 ‎1，23个3相乘，积的个位数字是几？‎ ‎2，100个2相乘，积的个位数字是几？‎ ‎3，50个7相乘，积的个位数字是几？‎ 例题4  有一列数按“432791864327918643279186……”排列，那么前54个数字之和是多少？‎ 思路导航：上面一列数中，从第1个数字开始重复出现的部分是“43279186”，周期数是8。要求出这列数字的和，就要先求出这列数里共有多少组“43279186”。‎ ‎54÷8=6（组）……6（个）‎ 因此，前6组数字和是（4＋3＋2＋7＋9＋1＋8＋6）×6=240，余下6个数字之和是4＋3＋2＋7＋9＋1=26。所以，这列数中前54个数字之和是240＋26=266。‎ ‎04‎ 小试牛刀 ‎1，一列数按“294736294736294……”排列，那么前40个数字之和是多少？‎ ‎2，有一列数按“9453672945367294……”排列，那么前50个数字之和是多少？‎ ‎3，有一列数“7231652316523165……”，请问从左起第2个数字到第25个数字之间（含第2个与第25个数字）所有数字的和是多少？‎ 例题5 小红买了一本童话书，每两页文字之间有3页插图，也就是说3页插图前后各有1页文字。如果这本书有128页，而第1页是文字，这本童话书共有插图多少页？‎ 思路导航：已知这本童话书3页插图前后各有1页文字，也就是说这本书是按“1页文字3页插图“的规律重复排列的，把“1页文字3页插图”看作一周期，128页中含有128÷（1＋3）=32个周期，所以这本童话书共有插图3×32=96页。‎ ‎05‎ 小试牛刀 ‎1，校门口摆了一排花，每两盆菊花之间摆3盆月季，共摆了112盆花。如果第一盆花是菊花，那么共摆了多少盆月季花？‎ ‎2，同学们做早操，36个同学排成一列，每两个女生中间是两个男生，第一个是女生，这列队伍中男生有多少人？‎ ‎3，一个圆形花辅周围长30米，沿周围每隔3米插一面红旗，每两面红旗中间插两面黄旗。花辅周围共插了多少面黄旗？‎ 三年级数学思维训练：有余除法 专题简析：‎ 把一些书平均分给几个小朋友，要使每个小朋友分得的本数最多，这些书分到最后会出现什么情况呢？一种是全部分完，还有一种是有剩余，并且剩余的本数必须比小朋友的人数少，否则还可以继续分下去。每次除得的余数必须比除数小，这是有余数除法计算中特别要注意的。‎ 解这类题的关键是要先确定余数，如果余数已知，就可以确定除数，然后再根据被除数与除数、商和余数的关系求出被除数。‎ 在有余数的除法中，要记住：‎ ‎（1）余数必须小于除数；‎ ‎（2）被除数=商×除数＋余数。‎ 有余除法 例题1  ‎ ‎□÷6=8……□，根据余数写出被除数最大是几？最小是几？   ‎ 思路导航：‎ 除数是6，根据余数比除数小，余数可填1、2、3、4、5，根据除数×商＋余数=被除数又已知商、除数、余数，可求出最大的被除数为6×8＋5=53，最小的被除数为6×8＋1=49。‎ 小试牛刀1:试一试，你能行的 ‎1，下面题中被除数最大可填几，最小可填几？‎ ‎  □÷8=3……□‎ ‎2，你能写出最大的被除数和最小的被除数吗？‎ ‎   □÷4=7……□‎ ‎3，下题中要使除数最小，被除数应为几？‎ ‎   □÷□=12……4‎ 例题2  ‎ ‎□÷□=8……15，要使除数最小，被除数应为几？ ‎ ‎ 思路导航：‎ 题中余数是15，除数应比余数就是比15大，比15大的有很多，但其中最小的应该是16。16是最小的除数，根据商×除数＋余数=被除数，就可以求出被除数了。所以应是：‎ ‎   8×16＋15=14‎ 小试牛刀2:试一试，你能行的 ‎1，下面算式中，要使除数最小，被除数应是几？‎ ‎   □÷□=12……10‎ ‎2，除数最小时，被除数是几？‎ ‎   □÷□=10……7‎ ‎3，你能写出下面的除数和商吗？‎ ‎  41÷□=□……1‎ 例题3  ‎ 算式28÷（  ）=（  ）……4中，除数和商各是多少？‎ 思路导航：‎ 根据“被除数=商×除数＋余数”，可以得知“除数×商=被除数－余数”，所以本题中商×除数=28－4=24。这两个数可能是1和24，2和12，3和8，4和6，又因为余数为4，因此除数可以是24、12、8、6，商分别为1、2、3、4。‎ 小试牛刀3:试一试，你能行的 ‎1，下列算式中，除数和商各是几？‎ ‎（1）22÷（  ）=（  ）……4‎ ‎（2）65÷（  ）=（  ）……2‎ ‎（3）37÷（  ）=（  ）……7‎ ‎（4）48÷（  ）=（  ）……6‎ ‎2，149除以一个两位数，余数是5，请写出所有这样的两位数。‎ 例4 算式（  ）÷7=（  ）……（  ）中，商和余数相等，被除数可以是哪些数？‎ 思路导航：‎ 题目中告诉我们除数是7，商和余数相等，因为余数必须比除数小，所以余数和商可为1、2、3、4、5、6，这样被除就可以求得了。‎ 小试牛刀4:试一试，你能行的 ‎1，下列算式中，商和余数相同，被除数是哪些数？‎ ‎（1）（  ）÷6=（  ）……（  ）‎ ‎（2）（  ）÷5=（  ）……（  ）‎ ‎（3）（  ）÷4=（  ）……（  ）‎ ‎（4）（  ）÷3=（  ）……（  ）‎ ‎2，一个三位数除以15，商和余数相等，请你写出五个这样的除法算式。‎ 例5 算式（  ）÷（  ）=（  ）……4中，除数和商相等，被除数最小是几？‎ 思路导航：‎ 题目中告诉我们余数是4，除数和商相等，因为余数必须比除数小，所以除数必须比4大，但其中要求最小的被除数，因而除数应填5，商也是5。5×5＋4=29，所以被除数最小是29。‎ 小试牛刀5:试一试，你能行的 ‎1，下面算式中，除数和商相等，被除数最小是几？‎ ‎（  ）÷（  ）=（  ）……6‎ ‎（  ）÷（  ）=（  ）……8‎ ‎（  ）÷（  ）=（  ）……3‎ ‎2，有一个除法算式，它的余数是9，除数和商相等，被除数最小是几？‎ 三年级数学思维训练：找规律 专题简析：‎ 按照一定次序排列起来的一列数，叫做数列。如自然数列：1、2、3、4……；双数列：2、4、6、8……。我们研究数列，目的就是为了发现数列中数排列的规律，并依据这个规律来填写空缺的数。‎ 按照一定的顺序排列的一列数，只要从连续的几个数中找到规律，那么就可以知道其余所有的数。寻找数列的排列规律，除了从相邻两数的和、差考虑，有时还要从积、商考虑。善于发现数列的规律是填数的关键。‎ 找规律一 例题1  在括号内填上合适的数。‎ ‎（1）3，6，9，12，（  ），（  ）‎ ‎（2）1，2，4，7，11，（  ），（  ）‎ ‎（3）2，6，18，54，（  ），（  ）‎ 思路导航：‎ ‎（1）在数列3，6，9，12，（  ），（  ）中，前一个数加上3就等于后一个数，相邻两个数的差都是3，根据这一规律，可以确定（  ）里分别填15和18；‎ ‎（2）在数列1，2，4，7，11，（  ），（  ）中，第一个数增加1等于第二个数，第二个数增加2等于第三个数，也就是相邻两个数的差依次是1，2，3，4……这样下一个数应为11增加5，所以应填16；再下一个数应比16大6，填22。‎ ‎（3）在数列2，6，18，54，（  ），（  ）中，后一个数是前一个数的3倍，根据这一规律可知道（  ）里应分别填162和486。‎ ‎ 小试牛刀:试一试，你能行的 ‎1.在括号里填数。‎ ‎（1）2，4，6，8，10，（  ），（  ）；‎ ‎（2）1，2，5，10，17，（  ），（  ）；‎ ‎2.按规律填数。‎ ‎（1）2，8，32，128，（  ），（  ）；‎ ‎（2）1，5，25，125，（  ），（  ）；‎ ‎3.先找规律再填数。‎ ‎12，1，10，1，8，1，（  ），（  ）‎ 三年级数学思维训练：找规律二 先哥微课堂 2019-07-02‎ ‎ ‎ ‎ ‎ 专题简析：‎ 按照一定次序排列起来的一列数，叫做数列。如自然数列：1、2、3、4……；双数列：2、4、6、8……。我们研究数列，目的就是为了发现数列中数排列的规律，并依据这个规律来填写空缺的数。‎ 按照一定的顺序排列的一列数，只要从连续的几个数中找到规律，那么就可以知道其余所有的数。寻找数列的排列规律，除了从相邻两数的和、差考虑，有时还要从积、商考虑。善于发现数列的规律是填数的关键。‎ 找规律二 例题2  先找出规律，再在括号里填上合适的数。‎ ‎（1）15，2，12，2，9，2，（  ），（  ）；‎ ‎（2）21，4，18，5，15，6，（  ），（  ）；‎ 思路导航：‎ ‎（1）在15，2，12，2，9，2，（  ），（  ）中隔着看，第一个数减3是第三个数，第三个数减3是第五个数，第二、四、六的数不变。根据这一规律，可以确定括号里分别应填6、2；‎ ‎（2）在21，4，18，5，15，6，（  ），（  ）中，隔着看第一个数减3为第三个数，第三个数减3为第五个数。第二个数增加1为第四个数，第四个数增加1是第六个数。根据这一规律，可以确定括号里分别应填12和7。‎ ‎ 小试牛刀:试一试，你能行的 ‎1.按规律填数。‎ ‎（1）2，1，4，1，6，1，（  ），（  ）；‎ ‎（2）3，2，9，2，27，2，（  ），（  ）；‎ ‎2.在括号里填数。‎ ‎（1）18，3，15，4，12，5，（  ），（  ）；‎ ‎（2）1，15，3，13，5，11，（  ），（  ）；‎ ‎3.找规律填数。‎ ‎   1，2，5，14，（  ），（  ）‎ 例题3  先找出规律，再在括号里填上合适的数。‎ ‎（1）2，5，14，41，（  ）；‎ ‎（2）252，124，60，28，（  ）；‎ ‎（3）1，2，5，13，34，（  ）；‎ ‎（4）1，4，9，16，25，36，（  ）；‎ 思路导航：‎ ‎（1）在数列2，5，14，41，（  ）中，第一个数2×3－1=5是第二个数，第二个数5×3－1=14是第三个数。依此类推，相邻两个数，前一个数乘3减1等于后一个数，所以括号里应填122。‎ ‎（2）在数列252，124，60，28，（  ）中，相邻的两个数，前一个数除以2的商减2等于后一个数，所以括号里应填12。‎ ‎（3）在数列1，2，5，13，34，（  ）中，可以发现2×3=1＋5，5×3=2＋13，13×3=5＋34，也就是从第二项开始，每一项乘3等于它前后相邻两数的和，因而括号里应填89。‎ ‎（4）这列数比较特别，第一个数1×1=1，第二个数2×2=4，第三个数3×3=9，可以看出它们分别为1，2，3，4，5，6…这些数自己与自己的乘积，因而第七个数为7×7=49。‎ ‎ 小试牛刀:试一试，你能行的 ‎1.按规律填数。‎ ‎（1）2，3，5，9，17，（  ）；‎ ‎（2）2，4，10，28，82，（  ），（  ）；‎ ‎2.按规律填数。‎ ‎94，46，22，10，（  ），（  ）‎ ‎3.在括号里按规律填数。‎ ‎   2，3，7，18，47，（  ），（  ）。‎ 找规律四 例题4  根据前面图形里的数的排列规律，填入适当的数。‎ 思路导航：‎ ‎（1）横着看，右边的比左边的数多5，竖着看，下面的数比上面的数多4。根据这一规律，方格里填18；‎ ‎（2）通过观察可以发现，前两个图形三个数之间有这样的关系：4×8÷2=16，7×8÷4=14，也就是说中心数是上面的数与左下方数的乘积除以右下方的数。根据这个规律，第三个图形空格中的数为9×4÷3=12；‎ ‎（3）横着看，第一行和第二行中，第一个数除以3等于第二个数，第一个数乘3等于第三个数。根据这一规律，36×3=108就是空格中的数。‎ ‎ 小试牛刀:试一试，你能行的 找出排列规律，在空缺处填上适当的数。‎ ‎ ‎ 广告 找规律五 例题5  按规律填数。‎ ‎（1）187，286，385，（  ），（  ）；‎ 思路导航：‎ ‎（1）在187，286，385，（  ），（ ‎ ‎ ）中，十位上的数字8不变，百位上的数字是1，2，3…依次增加1，个位上的数字是7，6，5…依次减少1，并且百位上的数字与个位上的数字的和为8。根据这一规律，括号里应填484，583；‎ ‎（2）通过观察可以发现，前两个图形之间有一定联系：左上数十位上的数字和右上数个位上的数字分别与下面数的千位、个位上的数字相同；左上数与右上数十位上的数字之和为下面数的百位上的数字，左上数与右上数个位上的数字之和为下面数的十位上的数字。根据这一规律，空格内应填3594。‎ ‎ 小试牛刀:试一试，你能行的 根据规律，在空格内填数。‎ ‎（1）198，297，396，（  ），（  ）；‎ 三年级数学思维训练：数图形 ‎ ‎ ‎ 专题简析：‎ 小朋友，你想学会数图形的方法吗？要想不重复也不遗漏地数出线段、角、三角形……那就必须要有次序、有条理地数，从中发现规律，以便得到正确的结果。要正确数出图形的个数，关键是要从基本图形入手。首先要弄清图形中包含的基本图形是什么，有多少个，然后再数出由基本图形组成的新的图形，并求出它们的和。‎ 数图形一 例题1  数出下面图中有多少条线段？‎ 思路导航：我们可以采用以线段左端点分数数的方法。‎ 以A点为左端点的线段有：AB、AC、AD共3条；‎ 以B点为左端点的线段有：BC、BD共2条；‎ 以C点为左端点的线段有：CD共1条。‎ 所以，图中共有线段3＋2＋1=6条。‎ 我们还可以这样想：把图中线段AB、BC、CD看作基本线段来数，那么：‎ 由1条基本线段构成的线段：AB、BC、CD共3条；‎ 由2条基本线段构成的线段：AC、BD共2条；‎ 由3条基本线段构成的线段：AD只1条。‎ 所以，图中共有3＋2＋1=6条线段。‎ ‎ 小试牛刀:试一试，你能行的 ‎1.数出下图中各有多少条线段？  ‎ ‎2.数出下图中有几个角。‎ ‎  ‎ 数图形二 例题2  数出下图中有几个角。‎ 思路导航：数角的个数可以采用与数线段相同的方法来数。‎ 以AO为一边的角有：∠AOB、∠AOC、∠AOD三个；‎ 以BO为一边的角有：∠BOC、∠BOD两个；‎ 以CO为一边的角有：∠COD一个。‎ 所以图中共有3＋2＋1=6个角。‎ 小朋友，如果把图中∠AOB、∠BOC、∠COD看作基本角，那应该怎样数呢？动动脑筋。‎ ‎ 小试牛刀:试一试，你能行的 ‎1.数出下图中有几个角？  ‎ ‎2.数出下图中有几个三角形？‎ 数图形二 例题2  数出下图中有几个角。‎ 思路导航：数角的个数可以采用与数线段相同的方法来数。‎ 以AO为一边的角有：∠AOB、∠AOC、∠AOD三个；‎ 以BO为一边的角有：∠BOC、∠BOD两个；‎ 以CO为一边的角有：∠COD一个。‎ 所以图中共有3＋2＋1=6个角。‎ 小朋友，如果把图中∠AOB、∠BOC、∠COD看作基本角，那应该怎样数呢？动动脑筋。‎ ‎ 小试牛刀:试一试，你能行的 ‎1.数出下图中有几个角？  ‎ ‎2.数出下图中有几个三角形？‎ 数图形三 例题3  数出下面图中共有多少个三角形。       ‎ 思路导航：数三角形的个数也可以采用按边分类的方法来数。‎ 以AB为边的三角形有：△ABC、△ABD、△ABE三个；‎ 以AC为边的三角形有：△ACD、△ACE二个；‎ 以AD为边的三角形有：△ADE一个。‎ 所以图中共有三角形3＋2＋1=6个。‎ 我们还发现，要数出图中三角形的个数，只需数出△ABE的底边中包含几条线段就可以了，即3＋2＋1=6条。所以图中共有6个三角形。‎ ‎ 小试牛刀:试一试，你能行的 ‎1.数出下面图中共有多少个三角形？  ‎ ‎2.数出下面图中共有多少个三角形？  ‎ 数图形四 例题4  数出下图中有多少个长方形。       ‎ 思路导航：数图形中有多少个长方形和数三角形的方法一样，长方形是由长、宽两对线段围成，线段CD上有3＋2＋1=6条线段，其中每一条与AC中一条线段对应，分别作为长方形的长和宽，这里共有6×1=6个长方形；而AC上共2＋1=3条线段也就有6×3=18个长方形。它的计算公式为：‎ 长方形的总数=长边线段的总数×宽边线段的总数 ‎ 小试牛刀:试一试，你能行的 ‎1.数出下图中有多少个长方形？  ‎ ‎2.数出下图中有多少个正方形？  ‎ 数图形五 例题5  有10个小朋友，每2个人照一张合影，一共要照多少张照片？‎ 思路导航：这道题可以用数线段的方法来解答。‎ 根据题意，画出线段图，每一个点代表一个小朋友：‎ 从图上可以看出，第1个小朋友要与其余9个小朋友合影，要照9张照片；第2个小朋友还要与其余8个小朋友合影，再照8张照片……以此类推，第9个小朋友只要再与1个小朋友合影，再照1张照片。所以，一共要照9＋8＋7＋6＋5＋4＋3＋2＋1=45张照片。‎ ‎ 小试牛刀:试一试，你能行的 ‎1.三年级有6个班，每两个班要比赛拔河一次，这样一共要组织多少场比赛？‎ ‎2.有红、黄、蓝、白四只气球，如果每两只气球扎成一束，共有多少种不同的扎法？‎ ‎3.有1——6六个数字，能组成多少个不同的两位数？‎ 三年级数学思维训练：年龄问题 年龄问题 ‎ ‎ 专题简析：年龄问题可以说是前面所讲的和差问题及差倍问题的综合，要正确解答这类题，首先要弄清：两个不同年龄的人，年龄之差始终不变，但两个人年龄的倍数关系却在不断地变化。年龄问题的主要特征是：大小年龄差是一个不变的量。我们可以抓住差不变这个特点，利用和差、差倍等知识来分析解答这类应用题。 例题1  三年前爸爸年龄是女儿的4倍，爸爸今年43岁，女儿今年多少岁？思路导航：由题意可知爸爸今年43岁，则三年前爸爸的年龄是43－3=40岁，40岁正好是女儿年龄的4倍，女儿三年前的年龄是40÷4=10岁，今年女儿的年龄是10＋3=13岁。 ‎ 练  习  一 1， 四年前小林年龄是小丽的2倍，小林今年12岁，小丽今年多少岁？‎ 2， 五年前爷爷年龄是孙子的7倍，孙子今年14岁，爷爷今年多少岁？‎ ‎3，儿子今年10岁，爸爸今年34岁。几年前，爸爸的年龄是儿子的4倍？‎ 例题2  明明4岁时，妈妈年龄是明明的8倍。今年明明12岁，妈妈今年多少岁？思路导航：妈妈的年龄是明明的8倍，那么妈妈与明明的年龄相差4×8－4=28岁。妈妈与明明的年龄差是不变的，今年明明12岁，那么妈妈的年龄是12＋28=40岁。‎ ‎ 练  习  二 1， 玲玲7岁时，爸爸年龄是玲玲的5倍。今年爸爸40岁，玲玲今年多少岁？‎ 1， 爷爷63岁时，他的年龄是小青的9倍。今年小青12岁，爷爷今年多少岁？‎ 2， 两年前妈妈年龄是儿子的5倍，儿子今年9岁，妈妈今年多少岁？‎ ‎ 例题3  女儿今年3岁，妈妈今年33岁。几年后，妈妈的年龄是女儿的7倍？思路导航：女儿今年3岁，妈妈今年33岁，她们的年龄差是33－3=30岁。她们年龄差不变，几年后，妈妈的年龄是女儿的3倍，把女儿的年龄看作1份，妈妈的年龄就有7份，相差7－1=6份，6份是30岁，所以几年后女儿的年龄是30÷6=5岁。也就是说，5－3=2年后，妈妈的年龄是女儿的7倍。 ‎ 练  习  三 ‎1，小明今年7岁，爷爷今年62岁。几年前，爷爷的年龄是小明的12倍？‎ ‎2，儿子今年2岁，爸爸今年的年龄是儿子的16倍。几年后，爸爸的年龄是儿子的7倍？‎ ‎3，妈妈今年26岁，是小玲年龄的13倍。几年后，妈妈的年龄是小玲的7倍？‎ ‎ 例题4  4年前，妈妈的年龄是女儿的3倍，4年后，母女年龄和是56岁。妈妈今年多少岁？思路导航：4年后，母子的年龄和是56岁，可求出今年母子年龄和是56－4×2=48岁。4年前母子年龄和是48－4×2=40岁。又根据4年前，妈妈年龄是女儿的3倍，把女儿年龄看作1份，妈妈的年龄就有这样的3份，共有3＋1=4份。所以4年前女儿的年龄是40÷4=10岁，妈妈今年的年龄是10×3＋4=34岁。 ‎ 练  习  四 ‎1，3年前，哥哥的年龄是弟弟的2倍。3年后，哥弟俩的年龄和是30岁。哥哥今年多少岁？2，5年前，小明的年龄是小红的3倍。5年后，小明和小红年龄和是44岁。今年小明多少岁？3，7年前，姐姐的年龄是妹妹的4倍。7年后，姐妹俩的年龄和是48岁。姐姐今年多少岁？‎ ‎ ‎ 例题5  明明今年12岁，强强今年7岁，当两人的年龄和是45岁时，两人各多少岁？思路导航：明明和强强的年龄差为12－7=5岁，这是一个不变量。当两人的年龄和是45岁时，明明比强强还是大5岁，如果从两人的年龄和45岁里减去两人的年龄差5岁，得到的就是两个强强的年龄。所以，强强的年龄是（45－5）÷2=20岁，明明的年龄是20＋5=25岁。 ‎ 练  习  五 ‎1，小红今年4岁，小平今年10岁，当两人的年龄和是30岁时，两人各多少岁？2，聪聪今年2岁，妈妈今年28岁。当母子俩的年龄和是42岁时，两人各多少岁？3，兰兰今年12岁，婷婷今年14岁，当两人的年龄和是40岁时，两人各多少岁？‎