- 3.09 MB
- 2021-12-06 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
小学数学五年级下册第五单元
异分母分数大小比较与通分
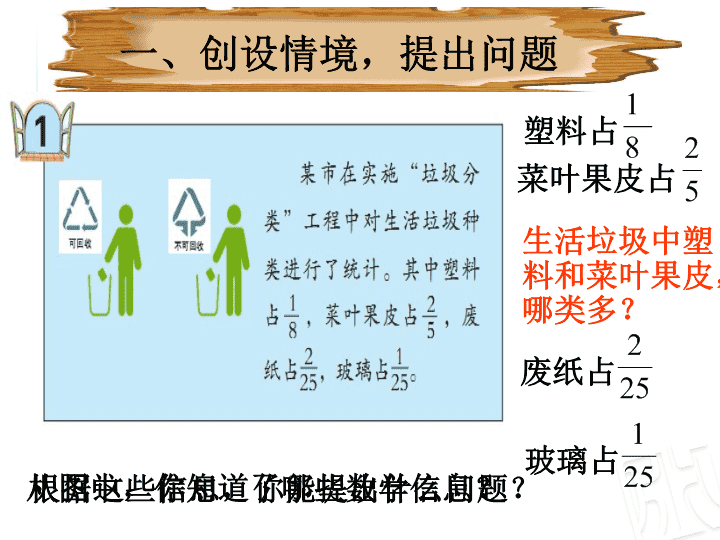
根据这些信息,你能提出什么问题?
生活垃圾中塑料和菜叶果皮,哪类多?
从图中,你知道了哪些数学信息?
玻璃占
废纸占
塑料占
菜叶果皮占
一、创设情境,提出问题
生活垃圾中塑料和菜叶果皮,哪类多?
比较 和 的大小就知道了。
二、自主学习,小组探究
思考:
怎么样才能知道生活垃圾中塑料
和菜叶果皮,哪类多呢?
塑料占
菜叶果皮占
异分母分数
生活垃圾中塑料和菜叶果皮,哪类多?
比较 和 的大小
二、自主学习,小组探究
探究提示:
(1)独立思考,想一想怎样做可以比较
和 的大小?
(2)动手画一画、折一折、算一算比较
和 的大小。
(3)组内交流你的比较方法和比较的依据是什么。
数形结合
化小数
化分子
生活垃圾中塑料和菜叶果皮,哪类多?
化分母
比较 和 的大小
二、自主学习,小组探究
画线段图
返回
画线段图比较
生活垃圾中塑料和菜叶果皮,哪类多?
<
三、汇报交流,评价质疑
借助学具比较
生活垃圾中塑料和菜叶果皮,哪类多?
三、汇报交流,评价质疑
<
返回
化成小数比较
生活垃圾中塑料和菜叶果皮,哪类多?
三、汇报交流,评价质疑
因为
0.125﹤0.4
<
=
1 ÷ 8
=
0.125
=
2
÷
5
=
0.4
所以
分数与除法的关系
依据
返回
化成分子相同的分数比较
生活垃圾中塑料和菜叶果皮,哪类多?
三、汇报交流,评价质疑
因为
所以
=
=
2
8
2
1
×
×
<
<
分数的基本性质
依据
可以化成
分子都是2
的分数
,
再比较。
返回
化成分母相同的分数比较
生活垃圾中塑料和菜叶果皮,哪类多?
三、汇报交流,评价质疑
因为
所以
=
=
=
=
5
8
5
1
×
×
8
5
8
2
×
×
<
<
分数的基本性质
依据
可以化成
分母都是40
的分数
,
再比较。
返回
异分母分数
同分母分数
和原来分数相等
分别化成
通分
三、汇报交流,评价质疑
把异分母分数分别化成与原来分数相等的同分母分数的过程,叫
通分。
通分时,相同的分母叫作这几个分数的
公分母。
=
=
=
5
8
5
1
×
×
=
8
5
8
2
×
×
公分母
你会把 和 通分吗?
2
4
1
2
继续
三、汇报交流,评价质疑
用
4
和
6
的
公倍数
作公分母,
把它们改写成分母相同而大小不变的分数。
返回
你会把 和 通分吗?
三、汇报交流,评价质疑
=
=
6
4
6
3
×
×
=
=
4
6
4
5
×
×
公分母
用
4
和
6
的
最小公倍数
作公分母,
把它们改写成分母相同而大小不变的分数。
你会把 和 通分吗?
三、汇报交流,评价质疑
=
=
3
4
3
3
×
×
=
=
2
6
2
5
×
×
返回
公分母
最小公倍数
想一想,通分时,哪个数作公分母比较简单?
三、汇报交流,评价质疑
通分时,通常用最小公倍数作公分母比较简便。
用公倍数做公分母:
用最小公倍数做公分母:
类比迁移 转化 数形结合
通分的意义:
根据分数的基本性质把异分母分数转化成与原来分数相等的同分母分数,这个过程就是
通分
。
通分时要注意:
先求出原来分母的最小公倍数作公分母,再看原来分数的分母变成公分母要乘上几,分子也要乘上相同的数。
通分的关键:
找准几个分母的最小公倍数作为公分母。
四、抽象概括,总结提升
1
.
垃圾回收。
五、巩固应用,拓展提高
20
3
6
72
15
30
3
2
.
把下面的各组分数通分。
五、巩固应用,拓展提高
2
.
把下面的各组分数通分。
五、巩固应用,拓展提高
=
=
=
=
8
5
8
4
×
×
5
8
5
7
×
×
和
互质关系
小结:
分母是互质关系,用分母的乘积作为公分母。
2
.
把下面的各组分数通分。
五、巩固应用,拓展提高
=
=
3
3
3
1
×
×
和
倍数关系
小结:
分母成倍数关系,较大的数就是公分母。
2
.
把下面的各组分数通分。
五、巩固应用,拓展提高
=
=
=
=
3
16
3
5
×
×
4
12
4
7
×
×
和
小结:用最小公倍数作公分母。
找最小公倍数
=
=
=
=
2
21
2
5
×
×
3
14
3
3
×
×
和
48
42
2
.
把下面的各组分数通分。
五、巩固应用,拓展提高
学以致用
通分时,一般先求出原来几个分母的最小公倍数,根据分数的基本性质,把各分数分别化成用最小公倍数作分母的分数。
3
.
比较每组两个分数的大小。
>
>
>
<
五、巩固应用,拓展提高
小结:
比较的方法很多,选择你喜欢并且简便的方法。
<
<
4
.
解决问题
方法一:计算折一只纸鹤谁用的时间最短。
方法二:计算折一分钟内谁折的只数最多。
<
<
>
>
答:
方方
折得
最快
。
我
6
分钟折
5
只纸鹤。
我
3
分钟折
2
只纸鹤。
我
5
分钟折
3
只纸鹤。
方方
明明
兰兰
谁折得快?
你是怎样算的?
与同学交流一下。
五、巩固应用,拓展提高
5
.
拓展延伸
五、巩固应用,拓展提高
根据分数的基本性质把这些分数化成分子相同的分数
同学们,今天我们得到了什么收获,最大的感受是什么?
相关文档
- 北师大版数学小学四年级下册教案-2021-12-062页
- 五年级上册数学教案-3统计(平均数)▏2021-12-064页
- 五年级上册数学课件 -6 可能性 ︳西2021-12-0616页
- 五年级语文上册新型玻璃2021-12-0614页
- 五年级上册美术课件-16画音乐 |浙美2021-12-0618页
- 北师大版五年级下册数学《分数乘法2021-12-0616页
- 人教PEP版 小学四年级下册英语-Uni2021-12-065页
- 五年级上册科学课件-1昼夜对动植物2021-12-0621页
- 五年级语文上册2落花生2021-12-064页
- 五年级上册数学课件-6质数和合数 2021-12-0615页