人教版五年级数学上册第六单元多边形的面积 习题课件 77页

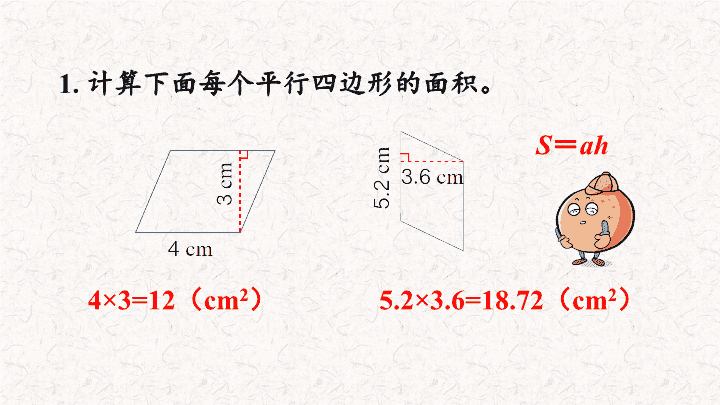
练习十九 多边形的面积 6 人教版 五年级 数学 上册 “割补” 法 底 高 长方形面积 = 长 × 宽 平行四边形面积 = 底 高 × 平行四边形面积公式的推导过程 用字母表示： S ＝ ah 1. 计算下面每个平行四边形的面积。 4 × 3=12 （ cm 2 ） 5.2×3.6=18.72 （ cm 2 ） S ＝ ah 2 × 2.4=4.8 （ cm 2 ） 或 : 3 × 1.6=4.8 （ cm 2 ） 1. 计算下面每个平行四边形的面积。 2. 有一块麦田的形状是平行 四边形。它的底是 250m ，高 是 84m ，共收小麦 14.7 吨。这 块麦田有多少公顷？平均每 公顷收小麦多少吨？ 250 × 84 14.7 ÷ 2.1=7 （吨） 答：这块麦田有 2.1 公顷，平均每公顷收小麦 7 吨。 =21000 （ m 2 ） =2.1 （公顷） 3. 一个平行四边形，它的底是 30cm ，高是 45cm ，它的面积是多少？ 30 × 45=1350 （ cm 2 ） 答：它的面积是 1350cm 2 。 S ＝ ah 4. 小明家门口有一个平行四边形的池塘，它的底是 34.2 米，高是 20.4 米，求这个池塘的面积是多少？ 34.2 × 20.4=697.68 （ m 2 ） 答：这个池塘的面积是 697.68m 2 。 5. 下面图中两个平行四边形的面积相等吗？它们的面积各是多少？ 2.8×1.5=4.2 （ cm 2 ） 答：底都是 2.8cm ，高都是 1.5cm ，所以面积相等，是 4.2 cm 2 。 6. 一下图中正方形的周长是 32cm 。 正方形的边长 32÷4=8(cm) 你能求出平行四边形的面积吗？ S = ah = 8×8 = 64 （ cm 2 ） 8cm 8cm 7. 同学们，你知道吗？大多数停车场里面的停车位都是平行四边形的，因为 这样是从斜侧角进入的，减少转弯角度，便于进、出车位 。某个停车场里有车位 660 个，每个车位的底都是 2.5 米，高是 5 米，这个停车场所有车位的占地面积是多少？ 2.5 × 5×660=8250 （ m 2 ） 答：有 车位的占地 面积 是 8250 平方米。 8. 右图中大平行四边形的面积是 48cm 2 。 A 、 B 是上、下两边的中点。你能求出图中小平行四边形（阴影部分）的面积吗？ 小平行四边形的 底 = 大平行四边形的 底的一半 小平行四边形的 高 = 大平行四边形的 高 小平行四边形的 面积 = 大平行四边形的 面积的一半 8. 右图中大平行四边形的面积是 48cm 2 。 A 、 B 是上、下两边的中点。你能求出图中小平行四边形（阴影部分）的面积吗？ 48÷2=24 （ cm 2 ） 答：阴影部分的面积是 24cm 2 。 这节课你们都学会了哪些知识？ 底 高 平行四边形面积 = 底 高 × 用字母表示： S ＝ ah 练习二十 多边形的面积 6 我们是怎样推导出三角形面积的计算公式的？ 三角 形 （新） 已学过的图形（旧） 转化（拼接、割补） 推导 联系 S ＝ ah ÷2 1. 指出下面每个三角形的底和高，并分别计算出它们的面积。 S = ah ÷2 = 3×4÷2 = 6 （ cm 2 ） S = ah ÷2 = 4×0.9÷2 = 1.8 （ dm 2 ） S = ah ÷2 = 2.5×2.8÷2 = 3.5 （ m 2 ） 2. 有一面大的三角形旗帜，它的底是 2.5 米，高是 1.2 米，这面旗帜的面积是多大？ 2.5×1.2÷2 =3÷2 =1.5 （ m 2 ） 答：这面旗帜的面积是 1.5 m 2 。 3 . 已知一个三角形的面积和底（如下图），求高。 由 S = ah÷2 变形，得 =16 （ m ） 4. 王老师到玻璃店配一块直角三角形的玻璃。这块玻璃有两条边相等，都是 40 厘米。如果每平方分米玻璃售价 6 元，配这块玻璃至少要用多少钱？ 已知条件 要求问题 40cm 40cm 40×40÷2÷100×6=48 （ 元 ） 答：配这块玻璃至少要用 48 元。 5 . 一块三角形地，底是 50 米，高是 11 米，如果一棵果树占地 5 平方米，那么这块地可栽果树多少棵？ 50×11÷2÷5 = 55 （棵） 答：可栽果树 55 棵。 三角形地面积 ÷ 每棵占地面积 = 可栽果树棵数 6. 现有一块长 10 m ，宽 1.5 m 的长方形红绸布，把它做成两条直角边都是 5 dm 的直角三角形小旗，可以做多少面？ 5 dm = 0.5 m 10×1.5÷ （ 0.5×0.5÷2 ） =120 （面） 答：可以做 120 面小旗。 长方形面积 ÷ 三角形小旗面积 = 可以做多少面 7. 一块三角形地，底长是 150 m ，高是 50 m ，共收油菜籽 1762.5 千克，平均每公顷产油菜籽多少千克？ 1 公顷 = 10000 m 2 1762.5 ÷ （ 150×50÷2÷10000 ） = 1762.5 ÷0.375 = 4700 （千克） 答：平均每公顷产油菜籽 4700 千克。 油菜籽总产量 ÷ 三角形地面积 = 平均每公顷产量 8. 埃及胡夫金字塔是现存的最大的金字塔，塔 身的石块之间，没有任何水泥之类的粘着物，而是一块石头叠在另一块石头上面的 。这座金字塔底边长约 220 米，从底边到顶点的距离约为 145.6 米，胡夫金字塔表面的面积是多少平方米？ 220×145.6÷2×4 = 32032÷2×4 = 16016×4 =64064m² 答 ：表面的面积是 64064 平方米。 9. 如图，平行四边形的面积是 60 m 2 ，求阴影部分的面积。 60÷6=10 （ m ） （ 10-7 ） ×6÷2=9 （ m 2 ） 答：阴影部分的面积为 9 m 2 。 10-7 10m 10. 要在公路中间的一块三角形空地（见下图）上种草坪。 1 m 2 草坪的价格是 12 元。种这片草坪需要多少钱？ 答：种这片草坪需要 912 元。 16 × 9.5÷2=76 （ m 2 ） 12 × 76=912 （ 元 ） 11. 下面中那几对三角形的面积相等？（两条虚线相互平行。） 由 S = ah÷2 可知，底、高都相等时，面积相等。 三角形 ABC 与三角形 DBC 面积相等 三角形 ABE 与三角形 DEC 面积相等 减去公共面积 12. 下面平行四边形底边的中点是 A ，它的面积是 48 m 2 。求涂色的三角形的面积。 阴影面积： 48× =12 （ m 2 ） 三角形 BCE 的面积 = 平行四边形面积的一半 三角形 ABC 的面积 = 三角形 BCE 的一半 B C D E 三角形 ABC 的面积 = 平行四边形面积的 这节课你们都学会了哪些知识？ 三角形的面积 = 底 × 高 ÷2 S ＝ ah÷2 练习二十一 多边形的面积 6 多边形的面积 我把一个梯形剪成了两个三角形。 我剪出了一个平行四边形和一个三角形。 两个一样的梯形可以拼成一个平行四边形。 怎样推导出梯形面积的计算公式的？ 梯形（新） 已学过的图形（旧） 转化（拼接、割补） 推导 联系 推导梯形面积的方策略 ： 梯形的面积 = （上底 + 下底） × 高 ÷2 S = （ a + b ） h ÷2 b a h 计算公式： 1. 制作小组制作飞机模型，机翼的平面图是由两个完全相同的梯形组成的（如下图）。机翼的面积是多少？ 250 mm 100 mm 48 mm 250 mm 100 mm 48 mm 机翼由两个梯形组成，可知 两个梯形完全相同 机翼的面积 = 两个梯形面积之和 = 其中一个梯形面积的 2 倍 250 mm 100 mm 48 mm 两个梯形完全相同 （ 48+100 ）× 250 ÷ 2 × 2 =18500 × 2 =37000 （ mm 2 ） 2. 一条新挖的水渠，横截面是梯形（如图）。渠口宽 2.8 m ，渠底宽 1.4 m ，渠深 1.2 m 。横截面的面积是多少平方米 ？ 利用梯形的面积公式计算出此水渠的横截面的面积。 （ 2.8+1.4 ）× 1.2 ÷ 2 = 4.2 × 1.2 ÷ 2 =5.04 ÷ 2 = 2.52 （ m 2 ） 答：横截面的面积是 2.52 平方米。 3. 一块梯形的花坛，上底是 2.4 m ，下底是 3.8 m ，高是 2.5 m ，要在花坛中间种花，每平方米种 40 株花，一共需要种多少株花？ 答：一共需要种 310 株花。 （ 2.4+3.8 ）× 2.5 ÷ 2 =6.2 × 2.5 ÷ 2 =7.75 （ m 2 ） 40 × 7.75=310 （ 株 ） 4. 计算下面每个梯形的面积。 （ 3 + 4 ） ×5÷2 =7×5÷2 = 17.5 （ m 2 ） （ 5.9 + 8.2 ） ×4.8÷2 =14.1×4.8÷2 = 33.84 （ cm 2 ） （ 12 + 15 ） ×20÷2 =27×20÷2 = 270 （ cm 2 ） 5. 靠墙边围成一个花坛，围花坛的篱笆长 46m ，求这个花坛的面积。 （ 46 - 20 ） ×20÷2 =26×20÷2 = 260 （ m 2 ） 上底 + 下底 = 46 - 20 = 26 （ m ） 答：这个花坛的面积是 260 m 2 。 梯形的面积 = （上底 + 下底） × 高 ÷2 6. 同学们，你们发现了吗？汽车的前挡风玻璃大都是梯形，这样的设计不仅美观，而且可以大大提高司机的视野。如果这种玻璃的造价是每平方米 600 元，算一算，这块玻璃的价格大概是多少元？ （ 100+145 ） ×70÷2 =245 × 70÷2 =17150÷2 =8575 （平方厘米） 8575 平方厘米 =0.8575 平方米 0.8575×600=514.5 （元） 答：这 块玻璃的价格大概 是 514.5 元。 7. 已知一个梯形的面积是 15c m 2 。它的上底是 4.5cm ，高是 3cm ，下底是多少厘米？（列方程解决） 解：设下底是 x cm 。 （ 4.5 + x ） ×3÷2 =15 4.5 + x =15×2÷3 x = 5.5 答：下底是 5.5 厘米。 8. 一个果园的形状是梯形。它的上底是 160m ，下底是 180 m ，高是 50m 。如果每棵果树占地 10 m 2 ，这个果园共有果树多少棵？ （ 160+180 ）× 50 ÷ 2 ÷ 10 = 8500 ÷ 10 = 850 （ 棵 ） 答：这个果园共有果树 850 棵 。 9. 在下面的梯形中剪去一个最大的平行四边形，剩下的面积是多少？有几种求法？ 方法一 梯形的面积 - 平行四边形的面积 梯形： (3.5+2)×1.8÷2=4.95 （平方厘米） 平行四边形： 2×1.8=3.6 （平方厘米） 剩下： 4.95-3.6=1.35 （平方厘米） 方法二 直接求剩下三角形的面积 (3.5-2)×1.8÷2 =1.5×1.8÷2 =1.35 （平方厘米 ） 9. 在下面的梯形中剪去一个最大的平行四边形，剩下的面积是多少？有几种求法？ 这节课你们都学会了哪些知识？ 梯形的面积 = （上底 + 下底） × 高 ÷2 S = （ a + b ） h ÷2 梯形的面积计算公式： 练习二十二 多边形的面积 6 方法一 方法二 方法三 方法四 解决组合图形的面积可以采取三种方法，就是 分、拼、挖 。 综合比较分析，针对 不同组合图形，要 选择 最简便 的解题方法。 不规则图形的面积 估算 数方格的方法进行估算 把不规则的图形转化为学过的图形进行估算 解决 不规则图形的面积 可以用估算法。 1. 一个指示牌的形状是一个组合图形，求它的面积。 20×10 + 20×10÷2 =200+100 = 300 （ cm 2 ） 长方形 + 三角形 2. 张伯伯在一块梯形地里建了一个长方形的鱼塘，余下的种菜，请求出这块菜地的实际面积是多少平方米。 （ 50+120 ）× 80 ÷ 2-20 × 30 =6800-600 =6200 （ m 2 ） 答：这块菜地的实际面积是 6200m 2 。 3. 小欣用一张红色不干胶纸剪了一个大写字母“ A ”。它的面积是多少？ (2+10)×12÷2 -3×4÷2 - (4+6)×4÷2 = 72-6-20 = 46 （ cm 2 ） 4. 下图是一间房屋的侧面墙，如果用石灰粉刷这面墙，每平方米用石灰 0.2 kg ，一共要用多少千克石灰？ 4.8×1.5÷2+4.8×3.2 =3.6+15.36 =18.96 （ m 2 ） 18.96×0.2=3.792 （ kg ） 答：一共要用 3.792 千克石灰。 5. 有一块地近似平行四边形，底是 43 m ，高是 20.1 m 。这块地的面积约是多少平方米？（得数保留整数。） S=ah = 43×20.1 =864.3 ≈ 864 （平方米） 答：这块地的面积约是 864 平方米。 6. 公园里有一块长方形的地 , 想种上红花、黄花和绿草 ( 如右图 ) 。你能分别算出红花、黄花、绿草的种植面积吗 ? 绿草 的面积占 长方形 面积 的一半 绿草的种植面积 ： 36×24÷2 36m 24m 红花 和 黄花 的面积各占 平行四 边形 的 一半 , 平行四边形又占 长 方形的一半 , 所以 红花和黄花 的 面积各占 长方形 面积的 36m 24m 6. 公园里有一块长方形的地 , 想种上红花、黄花和绿草 ( 如右图 ) 。你能分别算出红花、黄花、绿草的种植面积吗 ? 36×24=864(m 2 ) 　 864÷2=432(m 2 ) 　 864÷4=216(m 2 ) 答 : 绿草的种植面积是 432 m 2 , 红花和黄花的种植面积各是 216 m 2 。 解答 : 36m 24m 6. 公园里有一块长方形的地 , 想种上红花、黄花和绿草 ( 如右图 ) 。你能分别算出红花、黄花、绿草的种植面积吗 ? 7. 2019 年 1 月 3 日上午 10 点 26 分，“嫦娥四号”探测器成功着陆在 月球背面， 并通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图，揭开了古老月背的神秘面纱。此次任务实现了人类探测器首次月背软着陆，首次月背与地球的中继通信，开启了人类月球探测新篇章 。下面是明明画的一个火箭图案，你能算出它的面积吗？ 11 20 60 8cm 5.5cm 11×5.5÷2+60×11+ （ 11+20 ） ×8÷2=814.25 （ cm² ） 答：明明画的火箭的面积是 814.25 平方厘米。 单位：厘米 这节课你们都学会了哪些知识？ 解决组合图形的面积可以采取三种方法，就是 分、拼、挖 。 解决 不规则图形的面积 可以用 估算法 。 练习二十三 多边形的面积 6 a h a h b h a S = ah S = ah ÷2 S = （ a ＋ b ） h ÷2 这一单元学了哪些知识？ 求 组合图形 的面积 1. 判断题。 （ 1 ） 两个面积相等的三角形，一定能拼成一个平行四边形。 （ ） （ 2 ） 平行四边形的面积等于一个三角形面积的 2 倍。 （ ） （ 3 ） 两个三角形面积相等，底和高也一定相等。 （ ） × × × 两个完全一样的三角形 与其等底等高的 三角形 有可能相等 24 × 12 = 288 （ cm 2 ） 答：它的面积是 288cm 2 2. 一张平行四边形的纸片，底是 24 cm ，高是 12 cm ，它的面积是多大？ S = ah 3. 一块三角形的地砖，它的底是 36 cm ，高是 15 cm ，它的面积是多少？ 36×15÷2 =540÷2 = 270 （ cm 2 ） 答：它的面积是 270cm 2 。 S = ah ÷2 4. 下 图是一个交通标识牌，它代表的意思是要减速慢行，同学们，看到这个标识牌要提醒父母开车要慢哦！这个近似三角形的标识牌底边长 6dm ，这条边上的高是 5dm ，每平方分米用 4.32g 油漆，这块标识牌一共需要多少克油漆？ 6×5÷2×4.32=64.8 （克） 答：这 块标识牌一共 需要 64.8 克油漆 。 5. 下面平行线间有三个图形 , 有关它们面积大小 的说法 , 正确的是 ( 　　 ) 。 A. 甲 > 乙 > 丙　　 B. 甲 = 乙 > 丙 C. 甲 = 乙 = 丙 D. 乙 > 甲 > 丙 B 6 . 一块梯形小麦田，它的上底是 30 m ，下底是 50 m ，高是 25 m ，这块麦田的面积是多少？ （ 30+50 ） ×25÷2 =80×25÷2 =1000 （ m 2 ） 答：这块麦田的面积是 1000m 2 。 S = （ a ＋ b ） h ÷2 7. 有一台收割机，作业宽度是 1.8 m 。每小时行 5 km ，大约多少小时可以收割完下边这块地？ 先运用 梯形 的 面积公式 计算出这块地的 面积 ，然后计算出收割机的 工作效率 ，最后算 工作时间 。 5 km=5000 m 1.8 × 5000=9000 （ m 2 ） （ 200+330 ）× 100 ÷ 2 =530 × 100 ÷ 2 =26500 （ m 2 ） 26500 ÷ 9000 ≈ 2.94 （ 小时 ） 答：大约 2.94 小时可以收割完这块地。 8. 下图是教室的一面墙。如果砌这面墙平均每 平方米用砖 185 块，一共需要用多少块砖？ 这个图形由一个 三角形 和 一 个长方形 组成，分别计算出 它们的 面积再求和 ，然后再 求出共需要的 砖的块数 。 5×4=20 （ m 2 ） 1.2×5÷2=3 （ m 2 ） 20+3=23 （ m 2 ） 185×23=4255 （ 块 ） 答：一共需要 4255 块砖。 9. 求下列图形涂色部分的面积。 54×27=1458 （ mm 2 ） （ 20+30 ） ×10÷2=250 （ mm 2 ） 1458-250=1208 （ mm 2 ） 答：涂色部分的面积是 1208mm 2 。 10. 在正方形的一组对边中 , 一条边增加 17cm, 另一条边减少 10cm, 这样就变成了梯形。这时梯形下底是上底的 4 倍。这个梯形的面积是多少 ? 梯形下底比上底长 : 17+10=27(cm) 上底为 : 27÷3=9(c m ) 下底是 : 9×4=36(cm) 梯形的高 : 10+9=19(cm) 。 思路解析： 10. 在正方形的一组对边中 , 一条边增加 17cm, 另一条边减少 10cm, 这样就变成了梯形。这时梯形下底是上底的 4 倍。这个梯形的面积是多少 ? 17+10=27(cm) 　 　 上底 : 27÷(4-1)=9(cm) 　　 下底 : 9×4=36(cm) (9+36)×(10+9)÷2 =45×19÷2 = 427.5(cm 2 ) 答 : 这个梯形的面积是 427.5 cm 2 。 规范解答： 这节课你们都学会了哪些知识？ a h S = ah a h S = ah ÷2 b h a S = （ a ＋ b ） h ÷2