5年级数学教案《分数与除法的关系》 7页

分数与除法的关系 教学内容： 小学数学五年级下册第14-15页 信息窗2 红点1、2 第1课时 教学目标：‎ ‎1、理解分数与除法的关系，会用分数表示两个数相除的商。‎ ‎2、通过操作活动、运用数学结合的探究方法，渗透转化思想，来理解分数与除法关系的知识，培养提出问题、解决问题的能力。‎ ‎3、在探究活动中体验成功的喜悦，培养积极的学习态度和创新能力，树立学数学、用数学的信心。‎ 教学重难点：‎ 教学重点：理解分数与除法的关系，会用分数表示两个数相除的商。‎ 教学难点：理解分数与除法的关系。‎ 教具、学具：‎ 教师准备：多媒体课件 学生准备：直尺、纸条、铅笔 教学过程：‎ 一、创设情境，提出问题 谈话引入：校园科技周里，同学们创作了大量的优秀作品，大家快来欣赏下面两幅作品吧！课件出示情境图：‎ 仔细观察情境图，你发现了哪些数学信息？‎ 生交流：做4幅粘贴画用了1米长的毛线；做4幅粘贴画用了3个圆片。‎ 根据上面的信息你能提出什么数学问题？‎ 学生交流：‎ ‎⑴平均每幅画用多少米毛线？‎ ‎⑵平均每幅画用用多少个圆片？‎ 二、自主学习，合作探究 师谈话：同学们提出的问题很有研究价值，那我们先来研究第一个问题吧？课件出示问题：做4副粘贴画用了1米毛线，平均每副粘贴画用毛线多少米？‎ 活动要求：‎ ‎1.读一读，把信息与问题连起来读一读，完整的理解题意。‎ ‎2.说一说，请列出算式，并说出这样列式的理由。‎ ‎3.算一算，借助长条纸片代表毛线，通过折一折，画一画的方式来解释自己的想法，并算出结果。并把你们研究成果在小组内交流，准备全班分享。‎ 教师参与学生探究的过程，倾听大家的想法，及时点拨，及时关注学困生的动态，并给予帮助，积极搜集交流素材。‎ 三、汇报交流，评价质疑 谈话：哪一组愿意把你们的研究成果，与大家分享！‎ ㈠除法与几分之一 ‎1.初步感知分数可以表示两个数相除的商。‎ 学生列式：1÷4＝‎ 质疑：为什么用除法列出算式？‎ 生1：因为把几米的毛线平均分做成粘贴画，求每幅粘贴画用多少米毛线。‎ 生2：只要把东西平均分，就要用到除法……‎ ‎【师概括】：看来“除法”是由“平均分”产生的，以突出除法意义的本质。‎ 思考：1÷4得多少？你是怎样想的？‎ 学生可能表示的结果：‎ ‎（1）1÷4=0.25（米）=25厘米 ‎（2）0.25米也是米，所以，1÷4= （米 ） ‎ ‎ 师总结： 看来两个整数相除的商不仅可以用整数或小数来表示，还可以用分数来表示。‎ ‎ 2.初步沟通除法与分数的关系。‎ 师质疑：1÷4=米，“米”是怎样想的？‎ 生：是这样的：把1米长的毛线平均做成4个粘贴画，每个粘贴画所需的毛线就是这根1米长的毛线的，是0.25米，也就是米。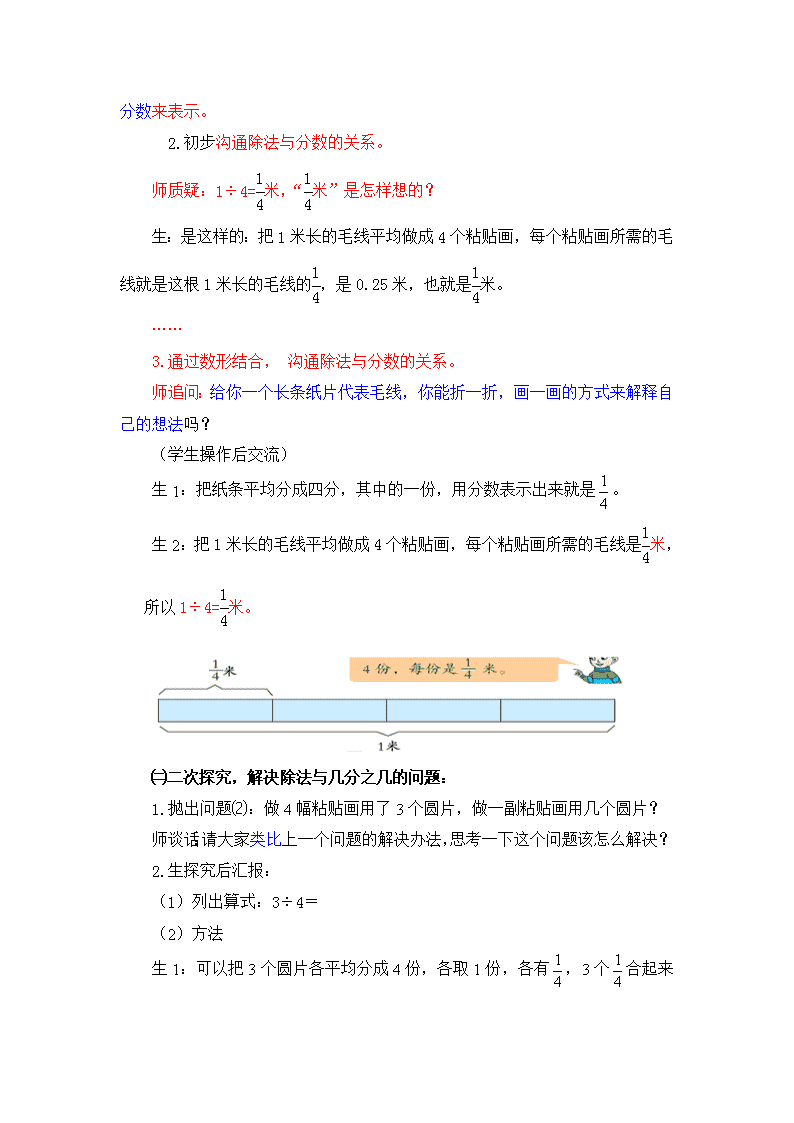‎ ‎……‎ ‎3.通过数形结合， 沟通除法与分数的关系。‎ 师追问：给你一个长条纸片代表毛线，你能折一折，画一画的方式来解释自己的想法吗？‎ ‎（学生操作后交流）‎ 生1：把纸条平均分成四分，其中的一份，用分数表示出来就是。‎ 生2：把1米长的毛线平均做成4个粘贴画，每个粘贴画所需的毛线是米，所以1÷4=米。‎ ㈡二次探究，解决除法与几分之几的问题：‎ ‎1.抛出问题⑵：做4幅粘贴画用了3个圆片，做一副粘贴画用几个圆片？‎ 师谈话：请大家类比上一个问题的解决办法，思考一下这个问题该怎么解决？‎ ‎2.生探究后汇报：‎ ‎（1）列出算式：3÷4＝‎ ‎（2）方法 生1：可以把3个圆片各平均分成4份，各取1份，各有，3个合起来是，如图示：‎ 生2：把3平均分成4份，每份是。所以3÷4=。 ‎ 如图示：‎ ㈢探索归纳分数与除法的关系。‎ ‎1.教师谈话引导 同学们认真观察下列式子：‎ ‎1÷4= ， 3÷4=……除法算式与它们对应的商有什么关系？ ‎ ‎2.学生对比思考 ‎3.学生交流 生1：商都是分数。‎ 生2：在1÷4=这个式子中，被除数1是分数的分子，除数是分数的分母，除号相当于分数线。‎ 生3：被除数相当于分数的分子，除数相当于分数的分母，除号相当于分数线，分数值相当于商。‎ ‎【师即时概括】：分数是一种数，除法是一种运算，所以确切地说，分数的分子相当于除法的被除数，分数的分母相当于除法的除数。（板书：相当于）‎ ‎4.分数与除法的关系 师：被除数相当于分数的分子，除数相当于分数的分母，除号相当于分数线，分数值相当于商。‎ 它们的关系可以表示为：‎ 教师板书： 被除数÷除数= ‎ 引导学生质疑：分数与除法有区别吗？‎ 生4：有，除法是一种运算，分数是一种数。‎ 师小结：除法是表示“平均分”的算式；分数是表示“平均分”的结果，是除法算式的商。分数是一个数，也可以看作两个数相除；除法是一种运算。‎ 质疑：分数的分母能为0吗？为什么？‎ 师启发学生说出在整数除法里，除数不能是0，除数为0就没有意义了，所以分数的分母也不能为0，即b≠0。‎ ‎5.用字母表示 谈话：如果分别用字母a和b表示除法算式中的被除数和除数，分数与除法的这种关系怎样表示？‎ 学生回答，师板书：a÷b= ‎ 谈话：大家考虑：这里的a和b是否可以是任何自然数？为什么？‎ 左侧b≠0，那么右侧的b是否可以是0？为什么？‎ 讨论完后，教师用红色粉笔标上： b≠0‎ 四、抽象概括，总结提升 刚才，通过大家的共同努力，我们研究了除法与分数的关系。‎ 分数与除法的联系 区别 除法 被除数 除号 除数 商 除法是一种运算。‎ 分数 分子 分数线 分母 分数 分数是一个数，也可以看作两个数相除。‎ 在研究的过程中，运用了数形结合的方法，渗透了转化的数学思想，来理解新知，直观形象，水到渠成。所谓转化的数学思想，就是由未知问题变换成可解的问题思想方法，在我们今后的数学学习中会经常用到。‎ 五、巩固练习，拓展延伸 ‎1、自主练习第2题：在括号里填上合适的数。‎ ‎①3÷5= ②8÷7= ③ =( )÷( ) ‎ ‎④ ( )÷9= ⑤13÷( )= ⑥( )÷( )=‎ 做题要求：‎ ‎（1）按顺序逐题出示；引导学生说明理由。‎ ‎（2）⑤⑥题有一定的开放性，答案不固定，只要合理都给与肯定。‎ ‎2、自主练习第3题 ‎ 平均每本《辞海》厚多少分米?‎ 做题要求 ‎①引导学生挖掘题目中的隐含条件（一共有几本《辞海》）；‎ ‎②引导学生发现求每本《辞海》厚度的方法?‎ ③运用分数与除法的关系，解决每本《辞海》厚多少分米?‎ ‎3、课后自主练习第9题（媒体逐一出示）‎ 在括号里填上适当的分数。‎ ‎ 做题要求：‎ ‎①找一找，以上不同单位间的进率分别是多少？‎ ‎②想一想，低单位化成高单位应该怎么办？‎ ‎③写一写，如何用分数表示结果?‎ 板书设计：‎ 设计说明：‎ 教学反思：回顾课堂，我感觉亮点之处有 ‎（1）创设情境，引发问题。‎ 本节课借助“小发明”活动情境，引出有价值的数学问题，在解决问题的过程中，感受用分数表示商的必要性，激发学生探究的积极性。‎ ‎（2）善用模型，注重直观。‎ 在沟通除法与分数之间的关系时，引导学生运用纸条、圆片通过折一折，画一画的方法，采取数形结合的方式，直观理解。‎ ‎（3）注重比较，理解新知。‎ 在总结概括“分数与除法的关系”时，通过对比引发思考，发现总结规律。培养发现问题和解决问题的能力.‎ 使用建议：‎ 学习过程中让学生充分利用现有素材，充分交流，经历知识的形成过程，使学生乐学。在总结结论时，应留给学生足够观察、思考、表达的时间，让结论内化，从而发展学生的观察分析能力和数学语言表达能力.‎ 需破解的问题：‎ 巩固练习第1题第⑥题( )÷( )=，答案不唯一，如何引导学生有序思考？‎