5年级数学教案《画折线统计图》 7页

画折线统计图 教学内容： 小学数学五年级上册103页信息窗1第2课时 教学目标：‎ ‎ 1.了解画单式折线统计图的一般步骤，会画单式折线统计图。能根据折线统计图中的数据变化情况进行分析和推测。‎ ‎ 2.在绘制折线统计图的过程中，经历数据的整理、分析与表示的过程，在观察、对比、交流、探究等学习活动中，体会和认识折线统计图的特点和作用，‎ ‎3.能够运用折线统计图的知识，解决身边的数学问题。‎ ‎4.感受折线统计图在实际生活中应用的广泛性和重要性，体验数学与日常生活的密切联系，更好地激发学习数学的兴趣。‎ 教学重点：描点、标数、连线，掌握绘制单式折线统计图的方法。‎ 教学难点：根据统计图表，合理确定横轴、纵轴上的数据位置。‎ 教具准备：多媒体课件。‎ 学具准备：方格纸（绘图用）、直尺、铅笔。‎ 教学过程：‎ 一、 创设情境，提出问题。‎ 1. 回顾旧知。‎ 谈话：上节课我们认识了折线统计图，谁来说说折线统计图有什么特点呢？‎ 学生回答后归纳：折线统计图有横轴，纵轴，单位，点，折线。点表示数量，折线表示数量的增减变化情况。‎ ‎2.直入课题。想亲手制作一张折线统计图吗？今天我们就来学习折线统计图的画法。（板书课题：画折线统计图）‎ ‎3.提出问题。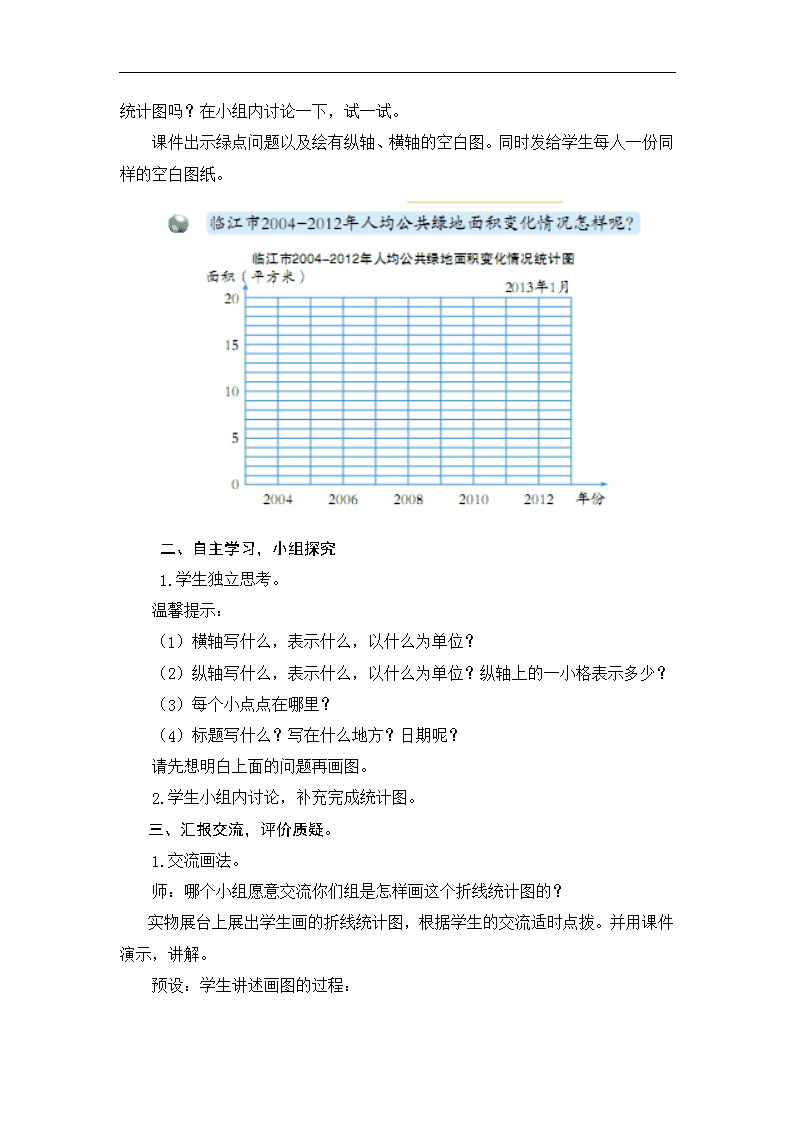‎ ‎ 再现信息：‎ ‎ 上节课我们用折线统计图表示了滨海市2004-2012年人均公共绿地面积变化情况，同学们还提到了临江市2004-2012年人均公共绿地面积变化情况怎样呢？‎ 那么你能把它绘成折线统计图吗？在小组内讨论一下，试一试。‎ 课件出示绿点问题以及绘有纵轴、横轴的空白图。同时发给学生每人一份同样的空白图纸。‎ ‎ ‎ ‎ 二、自主学习，小组探究 ‎ 1.学生独立思考。‎ 温馨提示：‎ ‎（1）横轴写什么，表示什么，以什么为单位？ ‎ ‎（2）纵轴写什么，表示什么，以什么为单位？纵轴上的一小格表示多少？‎ ‎（3）每个小点点在哪里？‎ ‎（4）标题写什么？写在什么地方？日期呢？‎ 请先想明白上面的问题再画图。‎ ‎2.学生小组内讨论，补充完成统计图。‎ 三、汇报交流，评价质疑。‎ ‎1.交流画法。‎ 师：哪个小组愿意交流你们组是怎样画这个折线统计图的？‎ 实物展台上展出学生画的折线统计图，根据学生的交流适时点拨。并用课件演示，讲解。‎ 预设：学生讲述画图的过程：‎ ①横轴：等间隔地标上年份，并在右边（ ）中标注单位。‎ ②纵轴：标注绿地面积，并在上方（ )中标注单位。‎ ③画点：根据统计表，在统计图相应的位置描点，并按顺序用线段依次连接各点。‎ ④标题：在 中写出标题，标题右下方写上日期。‎ 交流：在描点、连线的过程中我们要注意什么问题？‎ 引导学生说出要找准数据点，并在连线时要依次连接。‎ ‎2.讨论绘图的合理性 ‎（1）引导学生根据此图说出2004—2012年临江市人均公共绿地面积情况变化情况，学生讨论交流，师给予适当指点和评价。‎ ‎ 师讲解：统计图中所表示的最大值，在数学中叫“上限”； 统计图中所表示的最小值，在数学中叫“下限”。“ 下限——上限”之间，就是这个统计图的表示范围。‎ 讨论：统计图中的数字“上限”和“下限”有什么要求吗？‎ 学生讨论。预设：上限要大于或等于统计表中的最大数；下限要小于或等于统计表中的最小。‎ （2） 师生分析统计图的不同画法对数据分析产生影响：统计图纵轴上每个单位长度表示的数量不同，画出的折线统计图就不同。每个单位长度表示的数较小时，折线统计图增加的幅度就大；每个单位长度表示的数较大时，折线统计图增加的幅度就小。‎ （3） 师生共同小结：合理的确定纵轴上数据的位置，我们应根据统计表中的最大值、最小值来确定一个最接近于他们的整数作为纵轴的上限和下限，然后再进行推算调整。‎ ‎3.分析推测。‎ ‎（1）观察上面的统计图，你有什么发现？‎ 预设：临江市2004-2012年人均公共绿地面积逐渐增加。‎ ‎ ‚临江市2004-2012年人均公共绿地面积呈上升趋势。‎ 质疑：‎ 你现在还能 看出每年的人均面积是多少吗？你是如何看出的？（结合学生回答，进一步明确：点，表示数量的多少。）‎ ‎ ‚你是怎样看出人均公共绿地面积呈上升趋势的？‎ 引导学生用“增加”“减少”“持续增加”来描述数量的变化，用“迅速”“明显”“缓慢上升（或下降）”来描述数量变化的幅度。（进一步明确：线，表示-数量的变化趋势。） ‎ 小结:我们从“点”与“线”两个维度，看懂数量的多少及数量的变化趋势，看来，从折线统计图上不仅能看出数量的多少，还能看出数据的变化趋势。所以呀，我们要学会画折线统计图，来帮助我们分析数据。‎ ‎（2）你能根据数据的变化预测一下2014年人均公共绿地面积数量吗？‎ 预设：17平方米、20平方米等。‎ 师质疑：我预测是14平方米，你觉得合理吗？为什么？‎ 引导学生发现这样预测不合理，因为从统计图上看出临江市2004-2012年人均绿地面积呈上升趋势，所以2014年应该比2012年要多。‎ 小结：折线统计图还能帮助我们根据数据变化趋势进行合理的预测，看来学会画折线统计图十分重要。‎ 四、抽象概括，总结提升 ‎1.总结概括。刚才，我们通过动手实践尝试画折线统计图，得出了折线统计图的一般画法（媒体演示）：‎ ‎（1）横轴：等间隔地标上时间，并在（ ）中标注单位。‎ ‎（2）纵轴：标注数量，使得最大刻度能表示最大数量，并在（ )中标注单位。‎ ‎（3）画点：根据统计表，在统计图相应的位置描点，标数，连线。‎ ‎（4）标题：在 中写出标题，标题右下方写上日期。‎ ‎（5） 统计图的不同画法对数据分析产生影响。‎ 强调：画折线统计图关键是横轴、纵轴上数据位置的确定。数据位置的确定合适了，这样画出来的统计图才是合理美观的。‎ ‎2.总结提升。点，能反映所统计的事物的数量的多少；线，能看出数量的变化趋势。用折线统计图进行数据分析，能帮助我们根据数据变化趋势进行合理的预测。‎ 五、 巩固应用，拓展提高 ‎ 1.“自主练习”第2题。‎ ‎（1）温馨提示：‎ 想一想，画什么统计图较 好？为什么？‎ ‚看一看，移动电话增长的幅 度大小在图上是如何体现的？‎ ƒ说一说，移动电话的数量是 怎这样变化的？你能分析一以下原因吗？‎ ‎（2）学生理解，要用折线统计图才能更好地反映2007-2012年某市拥有移动电话的数量的增长变化情况。然后独立完成画折线统计图。教师巡视了解画图情况，帮助有困难的学生及时完成练习。‎ ‎（3）学生对图中折线反映出来的数量变化情况进行深入地分析，除明确变化规律（移动电话的数量始终呈递增趋势）外，还要找到发生变化的原因（原因是人们生活水平普遍提高），推想未来发展趋势。‎ ‎ 2.自主练习第3题。‎ （1） 让学生在独立观察思考的基础上，通过交流对锻炼成绩做出合理分析。‎ ‎ 预设：前3周，由于小彬刚开始锻炼，成绩没有明显地提高。但随着时间的推移，从第4周开始所用时间呈递减趋势，成绩也越来越好，到第7周，小彬跑1500米，只用6.3分钟。‎ （2） 在推测第8周成绩时，教师要适当引导，提示学生在合理的取值范围内进行推测。‎ （1） 在提出问题时，可以放手让学生提出有价值的问题，如：如果小彬坚持一直锻炼，跑1500米的时间会无限递减下去吗？教师给与指导，让学生明确：不会，人奔跑的速度是有极限的，不可能无限快下去(可以向学生介绍1500米长跑世界纪录是3分36秒46 )。‎ ‎3.《新课堂》95页第3题，学生独立完成。结合练习内容，向学生进行保护环境、节约用水的教育。‎ ‎4.课外实践：自主练习第5题。‎ 习题处理建议：‎ ‎（1）分组组织调查活动，通过合理渠道获取可靠的数据。‎ ‎（2）独立思考确定纵轴数据的方法，完成折线统计图的绘制。‎ ‎（3）分析交流：观察这个统计图，哪年在校人数最多？哪年在校人数最少？在校学生人数的整体的变化是怎样的？ ‎ ‎ 5.全课总结。通过本节课的学习，你有哪些收获？‎ 板书设计： ‎ ‎ 画 折 线 统 计 图 ‎ 横轴 纵轴 描点 标数 连线 标题 日期 使用说明：‎ ‎ 1.教学反思。 ‎ ‎（1）引导自主操作，注重学法指导。‎ 教学时，充分借助学生已有的认知基础和生活经验，运用迁移规律，让学生自主操作，教师在教学的关键处进行合理引导，学生学得扎实、有效。在学生亲自动手绘制折线统计图的过程中，培养了学生的认真细致的品质。‎ ‎（2）择取现实例子，体现统计价值。‎ 本课注重择取学生熟悉的、身边的生活例子，如对“联合国人居奖”问题比较感兴趣，为学好本节课内容打下了良好的基础。特别是最后一道练习题“课外调查”，更是让学生感知身边就有数学，学会用数学的眼光去观察、分析现实生活，增强应用数学的意识。‎ （3） 运用媒体，注重直观形象。‎ ‎ 折线统计图对于学生来说认识起来比较抽象，难懂，特别是制作时的步骤，充分利用多媒体的形象直观来教学，既让学生感知和体验了折线统计图的制作过程，也在学生头脑中构建了规范美观的折线统计图的形象。‎ ‎2.使用建议。如有学生熟悉的、合适的其它情景，可替换下临江市2004——2012年人均公共绿地面积情况统计的情景。选取更具时效性、更贴近学生生活的素材。‎ ‎3.需破解的问题。怎样联系学生的生活，让他们从中学到折线统计图的知识，并会合理的预测？ ‎