四年级数学《 加减法各部分之间的关系》经典教案 14页

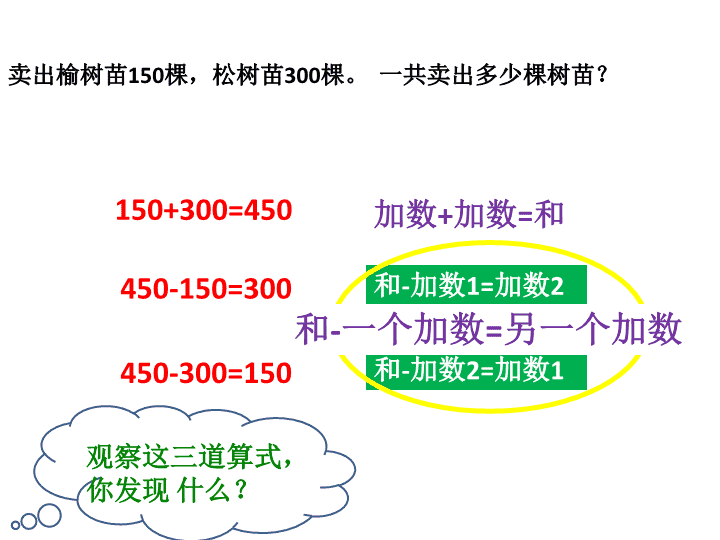
小学数学四年级下册 加减法各部分之间的关系 复习旧知，情境导入。 面对问题，合作探索。 自主练习，巩固方法。 回顾反思，总结提升。 前两个数相加再加第三个数，或后两个数相加再加第一个数和不变。 温故知新 两个数相加，交换加数的位置，它们的和不变。 卖出榆树苗 150 棵，松树苗 300 棵。 一共卖出多少棵树苗？ 卖出榆树苗和松树苗共 450 棵，其中榆树苗 150 棵。 松树苗多少棵？ 卖出榆树苗和松树苗共 450 棵，其中松树苗 300 棵。 榆树苗多少棵？ 150+300=450 450-150=300 450-300=150 观察这三道算式， 你发现 什么？ 加数 + 加数 = 和 和 - 加数 1= 加数 2 和 - 加数 2= 加数 1 和 - 一个加数 = 另一个加数 加数 + 加数 = 和 4 813-600=213 813-213=600 c-a=b c-b=a 验证规律 分享思考过程 加数 + 加数 = 和 和 - 一个加数 = 另一个加数 100-74=26 26+74=100 被减数 - 减数 = 差 被减数 - 差 = 减数 减数 + 差 = 被减数 100-26=74 减 法 各 部 分 之 间 的 关 系 知识迁移 被减数 - 减数 = 差 被减数 - 差 = 减数 减数 + 差 = 被减数 加数 + 加数 = 和 和 - 一个加数 = 另一个加数 加法和减法互为 逆运算 。减法算 式中的 被减数 相当于加法算式中的 和， 都是 整体 ；减法算式中的 减数 和 差 相 当加法算式中的两个 加数， 都是 部分 。 总结发现 减法各部分之间的关系 加法各部分之间的关系 整体 部分 总结提升 1. 不计算，直接写出后面算式的结果。 600-150=450 450+150= 600-450= 560-300=260 260+300= 560-260= 观察左面的算式，加、减法各部分之间有怎样的关系？减法和加法之间有什么关系？ 600 150 560 300 被减数 - 减数 = 差 差 + 减数 = 被减数 被减数 - 差 = 减数 加数 + 加数 = 和 和 - 一个加数 = 另一个加数 减法是加法的逆运算。 巩固应用 2 . 算一算，填一填。 680- （ ） =320 （ ） +400=1000 （ ） -125=475 360 600 600 被减数 - 差 = 减数 和 - 一个加数 = 另一个加数 差 + 减数 = 被减数 巩固应用 回顾反思 3. 计算并验算。 458+542= 900-805= 458 +542 1000 542 +458 1000 验 算 验 算 1000 - 542 458 1000 458 542 900 805 95 900 95 805 805 + 95 900 减数 = 被减数 - 差 被减数 = 差 + 减数 一个加数 = 和 - 另一个加数 加法交换律 1000 95 巩固应用 11 … 77 … 27 17 7 1 11 21 … 71 … … 51 … 21 11 1 2 12 … 42 … … 75 … 25 15 5 拓展提高 1 2 3 … 86 … 109 … 9 8 7 … 14 … 1 … 3 13 23 … 83 … 183 … 7 17 27 … 117… 217… 加法结合律、加法交换律以及加 减法各部分之间的关系帮助我们 简捷快速地解决问题。 拓展提高 （ 1 ）从学校到少年宫有几条路可走？ （ 2 ）走哪条路最近？近多少米？ （ 1 ）从学校到少年宫有 2 条路可走。 a. 比路的总长度。 407+418=825 （米） 392+506=898 （米） 898-825=73 （米） 答：经过邮局的近，近 73 米。 b. 两段路分别比。 407-392=15 （米） 506-418=88( 米 ) 88-15=73 （米） 答：经过邮局的近，近 73 米 （ 2 ） 同一个问题不同的解决方法， 你要灵活选择。 拓展提高 加法运算律 加法结合律 ( a+b)+c=a+(b+c) 加法交换律 a+b=b+a 简便计算 验算 加减法各部分之间的关系 加数 + 加数 = 和 和 - 一个加数 = 另一个加数 被减数 - 减数 = 差 被减数 - 差 = 减数 减数 + 差 = 被减数 发现知识之间的联系就是创造！ 抓住事物之间联系，开心玩数学！ 收获多多 旧知 新知