5年级数学教案《公因数和最大公因数》 7页

公因数和最大公因数 ‎ ‎ ‎ 教学内容： 小学数学五年级下册第29-31页信息窗1，第1、2个“红点”内容，以及自主练习部分习题。‎ 教学目标：‎ 结合解决问题理解公因数和最大公因数的意义，学会找两个数的最大公因数的方法。‎ ‎ 2.在探索公因数和最大公因数意义的过程中，经历观察、猜测、归纳等数学活动，进一步发展初步的推理能力。在解决问题的过程中，能进行有条理、有根据地进行思考。‎ ‎3.学会用公因数、最大公因数的知识解决简单的现实问题，体验数学与生活的密切联系。‎ ‎4.在学生探索新知的过程中，培养学生学好数学的信心以及小组成员之间互相合作的精神。‎ 教学重点：理解公因数、最大公因数的意义。‎ 教学难点：选用恰当的方法找两个数的最大公因数。‎ 教具准备：多媒体课件。‎ 学具准备：若干张长24厘米，宽18厘米的长方形纸；若干张边长1—7厘米的各种正方形纸。‎ 教学过程：‎ 一、 创设情境，提出问题。‎ 谈话：寒假前夕，我校德育处号召全校同学在寒假期间积极开展手工艺制作与综合实践活动 ‎。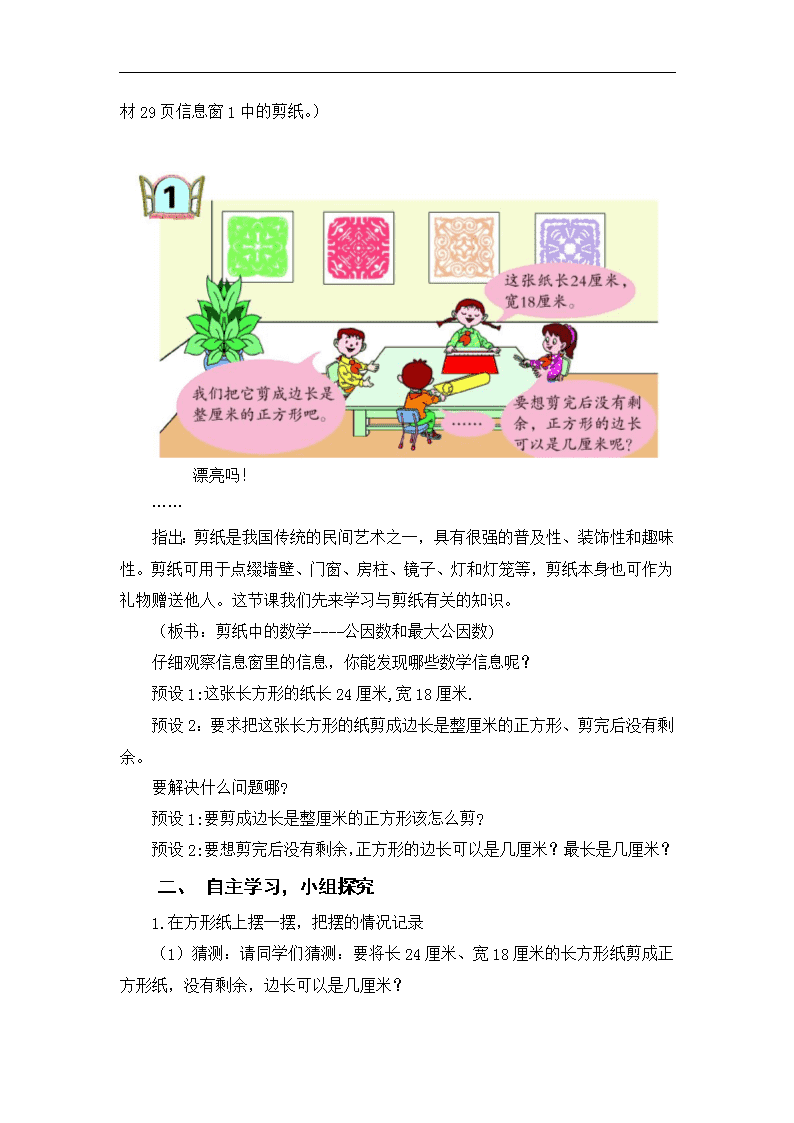我校的笑笑和淘气都是心灵手巧的孩子，寒假期间，他俩分别学习制作了民间艺术之一：剪纸。瞧！他们的剪纸还挺漂亮呢！（多媒体出示教材29页信息窗1中的剪纸。）‎ ‎ 漂亮吗！ ‎ ‎……‎ 指出：剪纸是我国传统的民间艺术之一，具有很强的普及性、装饰性和趣味性。剪纸可用于点缀墙壁、门窗、房柱、镜子、灯和灯笼等，剪纸本身也可作为礼物赠送他人。这节课我们先来学习与剪纸有关的知识。‎ ‎（板书：剪纸中的数学----公因数和最大公因数) ‎ 仔细观察信息窗里的信息，你能发现哪些数学信息呢？‎ 预设1:这张长方形的纸长24厘米,宽18厘米.‎ 预设2：要求把这张长方形的纸剪成边长是整厘米的正方形、剪完后没有剩余。‎ 要解决什么问题哪?‎ 预设1:要剪成边长是整厘米的正方形该怎么剪?‎ 预设2:要想剪完后没有剩余，正方形的边长可以是几厘米？最长是几厘米？‎ 一、 自主学习，小组探究 ‎1.在方形纸上摆一摆，把摆的情况记录 ‎（1）猜测：请同学们猜测：要将长24厘米、宽18厘米的长方形纸剪成正方形纸，没有剩余，边长可以是几厘米？‎ 预设1：边长可以是1厘米、2厘米、3厘米等。‎ ‎（2）验证：怎样验证你们的猜想呢？‎ ‎（学生自由回答，充分的发挥想象）‎ 预设：可以拿正方形纸片摆一摆。‎ 这是个好办法。‎ 教师演示：（先用边长是1厘米的正方形分别从长方形的长和宽来演示，用课件演示过程）‎ ‎2.你能得出什么结论？‎ 结论：用边长1厘米的正方形摆没有剩余。‎ ‎3.教师进而引出：用其他的正方形来摆有没有剩余呢？请同学们拿出准备好的学具，用正方形纸在长方形纸上摆一摆，看有几种不同的摆法。‎ 想一想：除了摆，还有其它的方法吗？‎ 学生在长方形纸上摆边长是2、3、4、5、6、7厘米的正方形。（学生分组进行摆，在小组内进行交流）‎ 一、 汇报交流，评价质疑。‎ ‎1.交流汇报。‎ 谁来说说你们是怎样验证的，又得出什么结论哪？‎ 预设1：用正方形纸在长方形纸上摆一摆（投影展示学生作品，并作适当的介绍）‎ 预设2：不用摆，算一算就知道 ‎ 比如：24÷3=8 18÷3=6‎ ‎ 因此，用边长3厘米的正方形纸片摆，正好可以摆满，没有剩余。‎ ‎ 从而得出结论：用边长1厘米、2厘米、3厘米、6厘米的正方形摆没有剩余，用边长4厘米、5厘米、7厘米的正方形摆有剩余。‎ 也就是说要想剪完后没有剩余，正方形的边长可以是1厘米、2厘米、3厘米也可以是6厘米，最长是6厘米。‎ ‎2.观察发现。‎ 同学们认真观察摆的结果，想一想：这些正方形的边长与长方形的长和宽有什么关系？‎ 预设：要想正好摆满，正方形纸片的边长应既是长方形长24的因数，也是长方形宽18的因数。‎ ‎3. 得出结论。‎ 预设：正方形的边长必须既是长方形长的因数，又是长方形宽的因数。‎ 教师总结：也就是找长方形长、宽的公有的因数。‎ ‎4. 明确公因数、最大公因数的意义。‎ 找出24和18的因数及公有的因数。‎ ‎（生在练习本上做后，集体交流。）‎ 在学生汇报的基础上，教师借助多媒体课件演示进一步讲解：‎ 师指出：两个数公有的因数叫做这两个数的公因数，其中最大的叫做这两个数的最大公因数。‎ ‎5.巩固练习：怎样找12和18 的公因数和最大公因数？‎ ‎ 请同学们试着用你喜欢的方法找一找12和18的公因数和最大公因数。‎ 启发学生用多种方法：‎ 提示学生“怎样找才能既不重复也不遗漏呢”？‎ 预设1：可以用集合图的形式 预设2：可以用列举的方法。‎ ‎6．学习用短除法求最大公因数。‎ 引导学生探索还有没有更简单的方法来求两个数的最大公因数？‎ 教师指出：还可以用短除法来求12和18的最大公因数。‎ 教师引导：‎ ‎①每次用什么做除数去除。‎ ‎②除到什么时候为止。‎ ‎③怎样求出最大公因数。‎ 教师规范短除法书写格式。‎ ‎④提问：你能用短除法求出16和28的最大公因数吗？‎ ‎(独立完成，全班交流)‎ 四、抽象概括，总结提升 ‎ 到目前为止我们可以采用哪几种方法来找两个数的公因数及求两个数的最大公因数？‎ 师生总结：找两个数的公因数及求两个数的最大公因数我们可以采用集合法、列举法及短除法。‎ 五、巩固应用，拓展提高 ‎1.自主练习第2题。‎ 填写集合图的题目，学生独立完成，集体订正。这里教师要进一步引导学生说出用集合图找最大公因数的方法和应注意的问题，向学生渗透集合思想。‎ ‎2.自主练习第3题。（用列举法找出每组数的最大公因数。）‎ 学生独立完成，集体订正。‎ ‎ 3.自主练习第4题。（用短除法求下列每组数的最大公因数。）‎ ‎ 分组完成（每组完成两个小题），并集体订正。‎ ‎4.自主练习第6题。‎ 利用公因数的知识解决实际问题。练习时教师要引导学生将生活中的问题转化为数学问题，即求“最多能扎多少束花”就是求48和72的最大公因数。然后让学生独立完成，交流订正 ‎5.课后总结：通过本节课的学习，说说你有哪些收获？（师生共同总结）‎ 板书设计：‎ 求两个数的公因数和最大公因数 两个数公有的因数叫做这两个数的公因数，‎ 其中最大的叫做这两个数的最大公因数。‎ ‎ ‎ ‎ 2 12 18 ……用公因数2去除 ‎ 3 6 9 ……用公因数3去除 ‎ 2 3 ……除到公因数只有1为止 ‎12和18的最大公因数是：2×3=6 ……把所有的除数乘起来 ‎ 教学反思：‎ 回顾整个教学过程，我感觉本节课有以下亮点：‎ ‎（1）充分放手，给学生提供自主探究的空间。‎ ‎ 在教学中，大胆放手，给学生提供了充分的自主探究的时间和空间。让学生带着问题、带着思考投入到学习中，大大提高了数学学习的实效性和针对性。‎ ‎（2）动手实践，经历概念的形成过程。‎ ‎ 在学生已有知识经验的基础上让学生去拼摆、交流、探索，在交流中形成概念。‎ 使用建议：‎ 首先用列举法和短除法找两个数的最大公因数，学生理解第一个红点的内容，便于学生理解.‎ 需破解的问题：‎ 利用短除法找最大公因数，每次除时，是否必须用两个数公有的“质因数”作除数？‎ ‎ ‎