五年级数学《组合图形的面积》 8页

组合图形的面积 教学内容 ‎ 小学数学五年级上册76页信息窗4 红点及小电脑的内容 教学目标 ‎1．结合生活实际认识组合图形，知道什么样的图形是组合图形,会求组合图形的面积。知道求组合图形的面积就是求几个基本图形的面积的和或差的计算。‎ ‎ 2．会把组合图形转化成学过的基本图形，体会“转化”策略，培养创新能力。‎ ‎3．能运用所学的知识，灵活解决生活中组合图形的实际问题，进一步发展学生的空间观念。‎ 教学重难点 重点：探索并掌握组合图形的面积的计算方法。难点：能正确将组合图形割补。‎ 教具、学具 教师准备：多媒体课件 学生准备：画有组合图形的纸片 直尺 教学过程 一、创设情景，提出问题 ‎1．同学们，到现在为止我们一共学过了计算哪些平面图形的面积？它们的面积计算公式分别是什么？‎ 预设：长方形的面积=长×宽 正方形的面积=边长×边长 ‎ 平行四边形的面积=底×高 三角形的面积=底×高÷2‎ ‎ 梯形的面积=（上底+下底）×高÷2‎ ‎2．谈话：同学们掌握的很好，这节课用这些知识继续探究平面图形的知识。‎ ‎3．出示信息窗四情境图 ‎ ‎ 师：你能知道哪些信息？‎ ‎ 预设：能知道虾池的形状是一个不规则的图形。其中有四条边的长分别是：30米 、90米、 80米 、40米。‎ ‎ 师：你能提出什么问题？‎ 预设：虾池的面积是多少平方米？‎ 师：怎样求虾池的面积呢？这节课我们一起来探究一下。‎ ‎ 二、自主学习，小组探究 ‎ 1 出示组合图及探究提示：‎ l 仔细观察，我们能直接计算虾池的面积是多少吗？为什么？（让学生认识到：不能直接求出虾池的面积是多少，因为这个虾池的形状不是规范的平面图形，是不规则图形。）‎ l 你能否想办法计算出虾池的面积呢？你是怎样计算的？‎ l 试一试还有别的计算方法吗？‎ ‎ 在图上画一画。生探究教师巡视并进行必要的指导。‎ 三、汇报交流、评价质疑 谁来汇报你们组是怎样求这个图形的面积的？学生边说边实物投影上演示。‎ 预设一：我们组把这个图形分成一个长方形和一个梯形，算出长方形和梯形的面积后，再加起来，得到的就是虾池的面积。如下图 ‎ ‎ 方法：S组合 =S长方形 +S梯形 ‎ 长方形面积： 80×40=3200（平方米） ‎ 梯形的面积： （30+80）×（90-40）÷2=2750（平方米） ‎ ‎ 组合图形的面积：3200+2750=5950（平方米） ‎ 师：你认为他们组的这种方法怎么样？哪个小组还有不同的方法？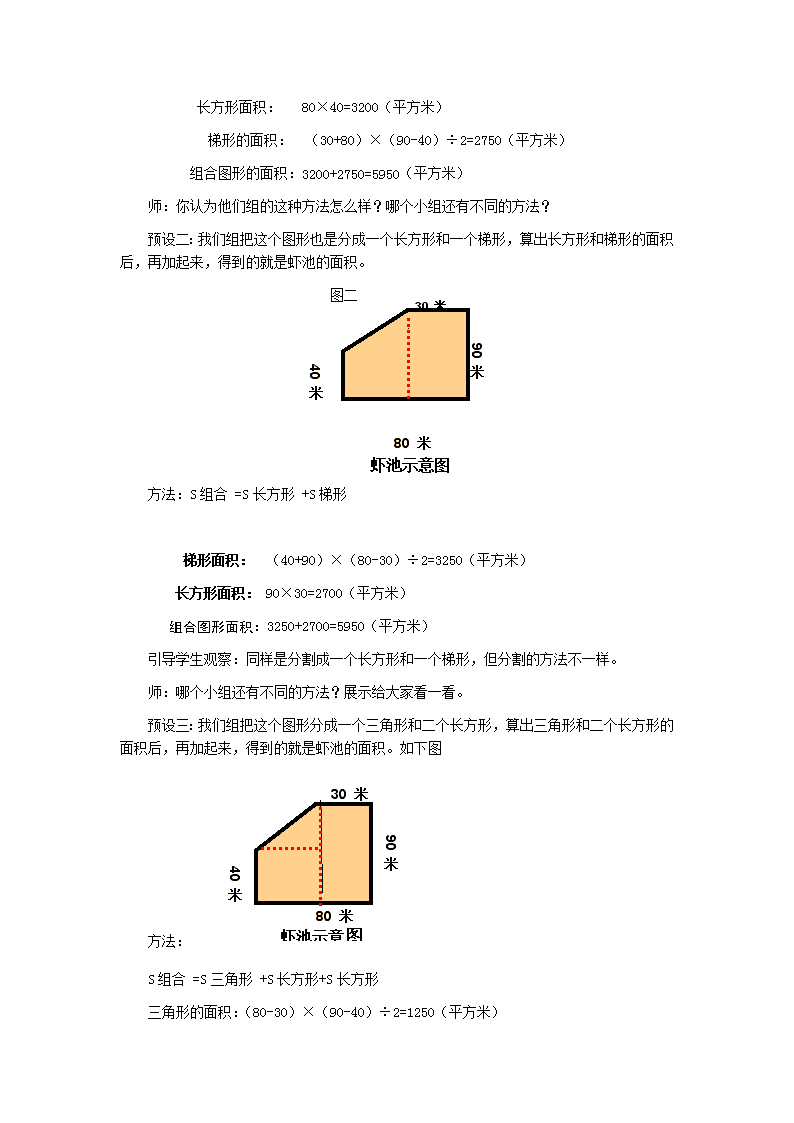‎ 预设二：我们组把这个图形也是分成一个长方形和一个梯形，算出长方形和梯形的面积后，再加起来，得到的就是虾池的面积。‎ ‎30 米 图二 ‎90 米 ‎40 米 ‎80 米 虾池示意图 ‎ 方法：S组合 =S长方形 +S梯形 梯形面积： （40+90）×（80-30）÷2=3250（平方米）‎ 长方形面积： 90×30=2700（平方米）‎ 组合图形面积：3250+2700=5950（平方米）‎ 引导学生观察：同样是分割成一个长方形和一个梯形，但分割的方法不一样。‎ 师：哪个小组还有不同的方法？展示给大家看一看。‎ 预设三：我们组把这个图形分成一个三角形和二个长方形，算出三角形和二个长方形的面积后，再加起来，得到的就是虾池的面积。如下图 ‎ 方法：‎‎30 米 ‎40 米 ‎90 米 ‎80 米 虾池示意图 ‎ S组合 =S三角形 +S长方形+S长方形 ‎ ‎ 三角形的面积：（80-30）×（90-40）÷2=1250（平方米）‎ ‎ 长方形的面积：40×（80-30）=2000（平方米） ‎ ‎ 长方形的面积：30×90=2700(平方米) ‎ ‎ 组合的面积：1250+2000+2700=5950（平方米）‎ ‎ 引导学生观察：这次是将图形分割成三角形和二个长方形，而算出三角形底和高是解题的关键。‎ 师：哪个小组还有不同的分法吗？展示给大家看一看。‎ 预设四：我们组把这个图形分成一个三角形和二个长方形，算出三角形面积和二个长方形面积，加起来，得到的就是虾池的面积。如图四 ‎30 米 图四 ‎40 米 虾池示意图 ‎ ‎80米 ‎90 米 方法：S组合=S三角形+S长方形+S长方形 三角形的面积：（80-30）×（90-40）÷2=1250（平方米）‎ 长方形的面积：40×80=3200（平方米）‎ 长方形的面积： 30×（90-40）=1500（平方米）‎ 组合图形面积：1250+3200+1500=5950（平方米）‎ 师：他们的方法对吗？你们还有其他方法吗？展示给大家看一看。‎ 预设五：我们组把这个图形分成一个三角形和三个长方形。‎ 虾池示意图 ‎ ‎30 米 ‎40 米 ‎90 米 ‎80 米 方法：S组合=S三角形+S长方形 +S长方形+S长方形 三角形面积:(80-30)×(90-40)÷ 2=1250(平方米)‎ 长方形面积：30 ×（90-40）=1500（平方米）‎ 长方形面积：30 ×40=1200（平方米）‎ 长方形面积：40 ×（80-30）=2000（平方米）‎ 组合图形的面积：1250+1500+1200+2000=5950（平方米）‎ 你认为他们组的这种方法可以吗？谁有问题可以向他提问。‎ 预设六：我们组把这个图形先补上一块，变成一个大长方形，然后用长方形的面积减去小三角形的面积，就是虾池的面积。如下图 米30‎ 图五 虾池示意图 ‎ ‎80 米 ‎40 米 ‎90 米 方法：S组合=S长方形-S三角形 长方形面积：90×80=7200（平方米）‎ 三角形面积：（90-40）×（80-30）÷2=1250（平方米） ‎ 组合图形的面积： 7200-1250=5950（平方米）‎ 质疑：这种方法与上面几种方法有什么区别？‎ 预设：上面几种方法是将组合图形分割成规范的图形，然后面积相加；这个是将组合图形添补成规范图形，然后面积相减。 ‎ ‎【设计意图】学生采用多种分割方法与添补法计算组合图形的面积，能形成多角度思考问题的习惯。‎ 试一试 ‎ ‎ ‎ 分割法 ‎ ‎ ‎ S组合图形=S平行四边形+S长方形 ‎ ‎30×6+30 ×10‎ ‎=180+300‎ ‎=480（平方厘米）‎ 添补法 S组合图形=S长方形-正方形 ‎15 ×12-5× 5‎ ‎=180-25‎ ‎=155（平方分 米）‎ 分割法 S组合图形=S梯形+S三角形 ‎（24+36）×8÷2+36×30÷2 ‎ ‎ =60×8÷2+1080÷2‎ ‎=240+540‎ ‎=780（平方厘米）‎ ‎ 四、抽象概括，总结提升 现在大家回忆一下我们是怎样来计算组合图形的面积的？‎ 预设：把组合图形分成我们学过的平面图形，分别算出各个小图形的面积之后再把面积加起来。‎ 预设：把组合图形再“补”上一块变成我们学过的平面图形，然后从大图形的面积里去掉补上的那个小图形的面积，就得到原图形的面积 师：结合学生的回答（课件出示）‎ 师：用割﹑补法计算组合图形面积时要注意什么？‎ ‎（1）要根据图形的特点，确定是用“割”还是用“补”的方法，“割”或“补”后的图形都应是规范图(2)“割”或“补”的平面图形越少越好，容易计算， “割”我们用加法算，“补”我们用减法计算。(3)“割”或“补”都要在图形上画了一些线，这些线需要借助尺子来画，一般要画成虚线。 ‎ ‎ 五、巩固应用，拓展提高 ‎ ‎1. 自主练习第1题：求下面图形的面积 ‎ ‎ ‎ 同学们先看这两幅图我们分别使用“割” 还是“补”的方法求面积好呢？‎ 在纸上先画一画找出最简便的方法再计算。‎ ‎ 2．自主练习第2题。求下列组合图形的面积 .‎ 学生分析：‎ 预设;S组合图形=S长方形+S三角形 ‎ ‎ 学生计算后展示：‎ ‎60 ×40+60 × 40÷ 2‎ ‎ =2400+120=3600（平方厘米）‎ ‎3.自主练习第6题 先让学生观察花坛平面示意图，再让学生说一说怎样求出草坪的占地面积。‎ 预设方法：用整个梯形的面积去掉中间小长方形的面积。‎ 预设列式：（8+10）×6÷2-3×2‎ ‎4．自主练习第7题.‎ 先分析题意：要求粉刷这面墙需要多少钱？需要先求出什么？这面墙是什么样的图形，面积怎样求？‎ 预设：先求出墙的面积，这面墙是一个组合图形，用长方形的面积加上三角形的面积就是这面墙的面积.‎ 预设列式：8×3.5+8×2÷2=36（平方米）‎ ‎ 36×10=360（元）‎ 板书设计： ‎ 组合图形的面积 观察 转化（分割、添补）‎ ‎（1）虾池的面积是多少？（其他方法课件显示）‎ ‎●分割法：把组合图形分割成学过的基本图形，分别算出面积后把面积相加。‎ 方法一：‎ ‎ ‎ ‎ ●添补法：把组合图形添补成学过的基本图形，分别算出面积后面积相减。‎ ‎ ‎ ‎ ‎