第5单元复习提升 81页

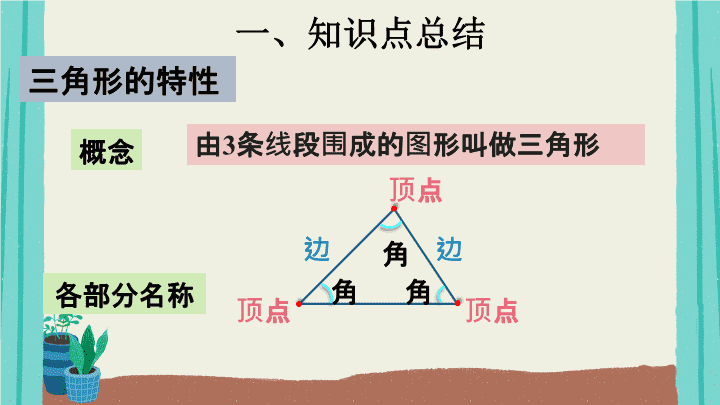
三角形 RJ 四年级下册 单元复习 你能找出图中的三角形吗？ 一、知识点总结 三角形的特性 概念 由3条线段围成的图形叫做三角形 各部分名称 顶点 顶点 顶点 边 边 角 角 角 一、知识点总结 三角形的特性 高 特性 顶点到它的对边作一条垂线，顶点和垂足 之间的线段叫做三角形的高 三角形具有稳定性 一、知识点总结 三角形的特性 两点间的距离 三边关系 两点间所有连线中线段最短 三角形任意两边的和大于第三边 一、知识点总结 等腰三角形 两边相等 三 角 形 的 分 类 锐角三角形 三个角都是锐角 按角分 按边分 直角三角形 有一个角是直角 等边三角形 三条边都相等 钝角三角形 有一个角是钝角 一、知识点总结 三 角 形 的 内 角 和 三角形的内角和是180° 三角形 内角和 四边形 内角和 四边形的内角和是360° 1.三角形的特性 二、典型知识点梳理 顶点 顶点 顶点 角 角 角 边 边 边 由3条线段围成的图形（每相邻两 条线段的端点相连）叫做三角形。 从三角形的一个顶点到它的对边 作一条垂线，顶点和垂足之间的 线段叫做三角形的高。 这条对边叫做三角形的底。 ﹉ A B C 三角形ABC，具有稳定性。 每个三角形有 多少条高？ 二、典型知识点梳理 【对应训练】 填一填 (1)由(　　)条线段(　　)成的图形(每相邻两条线段的端点 相连)叫做三角形。 (2)三角形有(　　　)条边，(　　)个顶点，(　　)个角。 3 围 3 3 3 二、典型知识点梳理 【对应训练】 (3)从三角形的一个(　　)到它的对边作一条(　　)， (　　)和(　　)之间的线段叫做三角形的高，这条对 边叫做三角形的(　　)。 (4)用字母A、B、C分别表示三角形的3个顶点，则三 角形可表示成( )。 顶点 三角形ABC 顶点 垂足 底 垂线 二、典型知识点梳理 2.三角形三边关系 4 5 9 6 7 8 （1） （2） 6 7 8 √ × 三角形任意两边的和大于第三边。 二、典型知识点梳理 【对应训练】 在能拼成三角形的各组小棒下面画“√”（单位：cm）。 √ √ √ （1） （3） （2） （4） （ ） （ ） （ ）（ ） 3.三角形的分类 二、典型知识点梳理 1个直角 2个锐角 1个钝角 2个锐角 直角三角形 钝角三角形 锐角三角形 按角进行分类 3个锐角： 二、典型知识点梳理 三条边相等 两条边相等 三条边都不等 等边三角形（正三角形） 等腰三角形 按边进行分类 二、典型知识点梳理 【对应训练】 选一选 (1)等边三角形中有(　　)个角相等。 A．1　　　　　　　 B．2 C．3 D．无法确定 (2)三条边的长度都是5 cm的三角形是(　　)。 A．锐角三角形 B．直角三角形 C．钝角三角形 D．无法确定 C A 二、典型知识点梳理 (3)等腰三角形一定是(　　)三角形。 A．锐角 B．钝角 C．直角 D．无法确定 D 4.三角形的内角和 二、典型知识点梳理 二、典型知识点梳理 【对应训练】 判一判 (1)一个直角三角形两个锐角的度数分别是25°和55°。 (　　) (2)在一个钝角三角形中，两个锐角的度数和小于90°。 (　　) × √ 二、典型知识点梳理 【对应训练】 (3)一个等腰三角形，顶角是56°，这一定是个锐角三 角形。 (　　) (4)在锐角三角形中，任何两个内角的度数之和一定大 于90°。 (　　) (5)三角形越大，它的内角和越大。 (　　) √ √ × 三、解决实际问题 一、填空。 (1)一个三角形中，其中两个角的度数分别是42°和73°，第三 个角的度数是(　　　)。 (2)如果一个三角形有两个内角的度数之和等于90°，那么这 个三角形一定是(　　　)三角形。 (3)等边三角形的三个内角都是(　　　)。 (4)一个等腰三角形中，顶角为80°，它的底角均为(　　)。 (5)在直角三角形中，一个锐角是54°，另一个锐角是(　　)。 65° 直角 60° 50° 36° 三、解决实际问题 二、小明从家到学校有3条路(如下图)，走(　　　)这 条路最近(填“上面”“中间”或“下面”)，为 什么？ 中间 两点之间， 线段最短。 三、解决实际问题 三、下面的数据，正确的画“ √ ”，错误的画“× ”。 √ × √ × 三、解决实际问题 四、下图是破损的三角形，猜猜看，它们原来是 什么三角形？ 直角 钝角 三、解决实际问题 五、如图，已知∠5＝90°，∠4＝50°，∠1＋∠2＝110° ，∠3＋∠4＝90°，求∠6的度数。 ∠3＝90°－50°＝40°， ∠1＝180°－90°－50°＝40°， ∠2＝110°－40°＝70°， 所以∠6＝180°－40°－70°＝70°。 RJ 4年级下册 第1课时　三角形的认识　 5 三角形 1．选择合适的方法画出下面的角，并说说它们分别 是哪一种角。 （选题源于教材P46第12题） 画角略。10°、45°、60°的角是锐角，90°的角是 直角，105°、120°的角是钝角，180°的角是平角。 1．看图填一填。 知识点 认识三角形 (1)在括号里标出各部分名称。 (2)三角形有(　　)条边，(　　)个角，(　　)个顶点。 (3)为了表达方便，上面的三角形可以表示为 (　　　　　　　)。 3 3 3 三角形ABC (4)从三角形的一个(　　　)到它的对边作一条(　　　)， (　　　)和(　　　)之间的线段叫做三角形的高，这条 对边叫做三角形的(　　)，三角形有(　　)条高。 顶点 垂线 顶点 垂足 底 三 2．判断下面的图形是不是三角形，是三角形的画 “√”，不是三角形的画“×”。 3．画出下面三角形底边上的高。 4．下面三角形指定底边上高的画法有误，请改正并填空。 易错警示：要画(　 　)底边上的高。 易错辨析 改正： 略 指定 5．下图中一共有(　　)个三角形。10 提升点 1 运用数线段的方法数三角形 6．画出下面三角形已知底边上的高。 提升点 2 画钝角三角形的高 7．如下图，摆1个三角形需要3根小棒，摆2个三角形 需要5根小棒……想一想其中的规律，摆15个三角 形需要(　　　)根小棒；用99根小棒可以摆(　　　) 个三角形。 31 49 RJ 4年级下册 第2课时　三角形的稳定性 5 三角形 1．选择合适的方法画出下面的角，并说说它们分别 是哪一种角。 （选题源于教材P46第12题） 画角略。10°、45°、60°的角是锐角，90°的角是 直角，105°、120°的角是钝角，180°的角是平角。 1．选择。(将正确答案的字母填在括号里) (1)用同样长的3根小棒可以围成(　　)三角形，用4根同样 长的小棒可以围成(　　)不同的四边形。 A．1个　 B．2个　 C．3个　 D．无数个 知识点 三角形的稳定性 A D (3)下列选项中稳定性最好、最不容易变形的是(　　)。 A．三角形 B．平行四边形 C．梯形 D．正方形 (3)篮球架上的篮板支架(如图)，是根据三角形具有(　　) 的特性设计的。 A．美观性 B．稳定性 C．不稳定性 D．以上都不对 B A 2．下面是篱笆的两种不同围法，你认为哪种围法更牢 固？为什么？ 右边的围法更牢固，因为三角形更稳定。 3．下图所示物体中都有三角形的结构，这些三角形结构 有什么作用？ 这些三角形结构能让物体更加稳定，起稳定作用。 易错警示：加上木条后与原来的椅子腿构成四边形 ，(　　　)变形，加上木条后应与原来的椅子腿构 成(　　　)。 4．明明这样加固这张椅子，他的做法有误，请改正并填 空。 图略(斜着钉一根木条，与原来的椅子 腿构成三角形) 易错辨析 改正： 易 三角形 5．盖房子时，在窗框未安装之前，木工师傅常常先在窗 框上斜钉一根木条(如图)，木工师傅为什么这样做？ 在窗框上斜钉一根木条可以构成三角形 ，三角形具有稳定性，使得窗框不易变 形。 提升点 运用三角形的稳定性解决实际问题 6．你见过人字梯吗？为什么工人师傅在人字梯中间 系一根绳子？ 在人字梯中间系一根绳子，可使人字梯 更稳固。 7．如果要使五边形和六边形木架不易变形该怎么办？ 请在图中画一画。 (画法不唯一) RJ 4年级下册 阶段小达标(7) 5 三角形 (1)照相机的支架有三条腿，这是利用了三角形的 (　　　　)。 (2)一个三角形的两条边的长分别是9厘米和5厘米，第 三条边最长是(　　)厘米，最短是(　　)厘米。(边 长是整厘米数) 稳定性 13 5 1．填空。(每空2分，共22分) (3)一个三角形，最大的角是80°，这个三角形是一个 (　　　)角三角形。 (4)一个三角形最多有一个(　　)角或(　　)角。 锐 直 钝 (5)一根铁丝可以围成一个底边长12厘米，腰长15厘米 的等腰三角形，若将这根铁丝改围成一个等边三角 形，围成的等边三角形的边长是(　　　)厘米。 (6)有三种小棒各若干，长度分别是3厘米、7厘米和10 厘米，选一根7厘米的小棒和两根(　　)厘米的小 棒可以围成一个底和腰不相等的等腰三角形。 14 10 (7)一个等腰三角形的两条边的长分别是8厘米和10厘米， 这个等腰三角形的周长可能是(　　)厘米，也可能是 (　　)厘米。 (8)一根长24厘米的铁丝首尾相连可围成一个三角形， 在围成的所有三角形中，最长的一条边一定要小于 (　　)厘米。(整厘米) 26 28 12 2．选择。(将正确答案的序号填在括号里。每小题3分， 共18分) (1)一个三角形中有一个角是锐角，这个三角形是(　　)。 A．锐角三角形 B．直角三角形 C．钝角三角形 D．无法确定 D (2)在直角三角形中，(　　)最长。 A．较长的直角边 B．斜边 C．不确定哪条边 B (3)数学课上，晓晓把一根木条锯成三段，长度分别是5厘米 、7厘米和12厘米，这三段木条能围成三角形吗？(　　) A．能 B．不能 C．不确定 (4)从6根分别是5厘米、5厘米、5厘米、10厘米、10厘米、9 厘米长的小棒中选取三根，可以摆出(　　)个不同的三 角形。 A．4　　　B．5　　　C．6　　　D．7 B B (5)所有的等边三角形都是(　　)。 A．锐角三角形 B．直角三角形 C．钝角三角形 D．无法确定 (6)爸爸给明明做了一个等腰三角形的风筝。已知风筝的 两条边的长分别是55厘米和27厘米，第三条边的长 是(　　)厘米。 A．80 B．55 C．27 D．30 A B 3．解决问题。(共20分) (1)李叔叔要给一块等腰三角形的菜地围上篱笆，一共 用了48米长的篱笆，这块菜地的底边长18米，腰长 是多少米？(10分) (48－18)÷2＝15(米) 答：腰长是15米。 (2)下面的每种小棒都有两根，任意取其中的三根，能 摆出几个不同的三角形？分别写出每个三角形三条 边的长度。(10分) 能摆出13个不同的三角形。(3厘米，7厘米，8厘米) (3厘米，7厘米，9厘米)(3厘米，8厘米，9厘米) (7厘米，8厘米，9厘米)(7厘米，7厘米，8厘米) (7厘米，7厘米，9厘米)(7厘米，7厘米，3厘米) (8厘米，8厘米，9厘米)(8厘米，8厘米，7厘米) (8厘米，8厘米，3厘米)(9厘米，9厘米，8厘米) (9厘米，9厘米，7厘米)(9厘米，9厘米，3厘米) RJ 4年级下册 阶段小达标 (8) 5 三角形 1．填空。(每空2分，共30分) (1)一个三角形的一个角是30°，另一个角是它的3倍， 它是一个(　　　)三角形。 (2)在一个等腰三角形中，如果底角是40°，则它的顶 角是(　　)°，按角分它是一个(　　　)三角形。 (3)一个三角形中，两个内角的和是86°，第三个内角 是(　　)°，这个三角形是(　　　)三角形。 直角 100 钝角 94 钝角 (4)一个直角三角形ABC，锐角∠A比∠B大30°， ∠A＝(　　)°，∠B＝(　　)°。 (5)当三角形中两个内角的和等于第三个内角时，这 是一个(　　　)三角形。 (6)一个三角形如果是直角三角形，这个三角形的三 个角分别是55°，(　　)°和(　　)°。 60 30 直角 35 90 (7)一个三角形中，∠1，∠2，∠3是它的三个内角， ∠1＝80°，∠1是∠2的2倍，则∠3＝(　　)°。 (8)右边是一块三角形玻璃打碎后的碎片，按角分它原 来是(　　　)三角形。 60 直角 (9)如果一个等腰三角形的顶角是底角的3倍，底角是 (　　)°；如果一个等腰三角形的底角是顶角的4 倍，顶角是(　　)°。 (10)已知一个多边形的内角和是1800°，这个多边形 是(　 　)边形。 36 20 十二 2．选择。(将正确答案的字母填在括号里。每小题2分， 共8分) (1)把一个等边三角形分成两个直角三角形，其中一个直 角三角形的两个锐角分别是(　　)。 A．30°和60°　　　　　B．45°和45° C．60°和60° A (2)把两个完全一样的三角形拼成一个四边形，这个四边形 的内角和是(　　)。 A．180° B．360° C．540° B (3)一个三角形的一个内角是80°，另外两个内角可能是 (　　)。 A．45°和65° 　B．60°和30°C．60°和40° (4)一个等腰三角形中，有一个角是40°，另外两个角不 可能是(　　)。 A．40°和100° B．70°和70°C．60°和80° C C 3．解决问题。(共22分) (1)如图，三角形ABD是一个等边三角形，∠ABC是直 角，求∠C的度数。(7分) ∠C＝180°－90°－60°＝30° 答：∠C是30°。 (2)如下图，在三角形ABC中，如果沿图中的线段DE将 ∠A剪掉，那么剩下部分的内角和是多少度？(7分) 剩下部分的内角和是360°。 (3)在一个三角形中，最大角的度数是最小角的3倍，另 一个角的度数是最小角的2倍，这个三角形的三个 角分别是多少度？(8分) 180°÷(3＋2＋1)＝30°　30°×2＝60° 30°×3＝90° 答：这个三角形的三个角分别是30°、60°、90°。 第11招 三角形内角和及边的关系的应用 RJ 四年级下册 一个等腰三角形的周长是28厘米，它的底边比一条腰长 的2倍少4厘米，这个三角形的底边长是多少厘米？ 经典例题 规范解答： (28＋4)÷(1＋1＋2) ＝32÷4 ＝8(厘米) 8×2－4＝12(厘米) 答：这个三角形的底边长是12厘米。 1 3 5 提示：点击 进入题组训 练 三角形内角和的应用2 4 6 三角形边的关系的实际应用7 三角形内角和的应用类 型 1 1．如图，在三角形ABC中，∠A＝60°，∠A比∠B多 15°，求∠C的度数。 ∠B＝ 60°－15°＝45° ∠C＝180°－60°－45°＝75° ∠B＝∠A－15° ∠C＝180°－∠A－ ∠B 2．计算下面正五边形和正六边形的内角和。 (5－2)×180°＝540° (6－2)×180°＝720° 多边形内角和计算公式：(n－2)×180° 3．如图所示，已知∠1＝40°，∠2＝20°，∠5＝ 90°，求∠3、∠4的度数。 ∠3＝180°－90°－40°＝50° 90°－20°＝70°　 180°－70°＝110° ∠4＝180°－40°－110°＝30° ∠3＝180°－∠1－∠5 ∠4＝180°－∠1－∠5－∠2 4．李大伯家的三角形菜地的两条边分别长8 m和10 m ，这块三角形菜地的周长最长是多少米？最短是多 少米？(第三条边的长是整米数) 三角形边的关系的实际应用类 型 2 三角形任意两边之和大于第三边 第三边＜10＋8 第三边最大是17m，三角形任意两边之差小于第三边 第三边＞10－8 第三边最小是3m 第三条边最短：10－8＋1＝3(m) 第三条边最长：10＋8－1＝17(m) 周长最长：10＋8＋17＝35(m) 周长最短：10＋8＋3＝21(m) 答：这块三角形菜地的周长最长是35m，最短是21m。 5．莹莹用一根铁丝围成了一个边长是20 cm的正方形。 如果用这根铁丝围成一个底边长是30 cm的等腰三角形 ，那么这个等腰三角形的腰长是多少厘米？ 正方形周长＝20×4＝80cm 腰长×2＋30＝80cm20×4＝80(cm) (80－30)÷2＝25(cm) 答：这个等腰三角形的腰长是25cm。 6．有一块等腰三角形的绿地，它的周长是164米，其中一 条边的长是52米，另外两条边的长分别是多少米？ 52米的边可能是底边，也可能是腰长 情况一：若腰长是52米。 164－52×2＝60(米) 情况二：若底边长是52米。 (164－52)÷2＝56(米) 答：另外两条边的长分别是52米和60米或56米和56米。 7．从下面6根小棒中任意取3根小棒组成一个三角形，可 以组成多少种不同的三角形？(单位：厘米) 三角形任意两边之和大于第三边 三角形任意两边之差小于第三边 可以组成13种不同的三角形。 ① 2厘米　3厘米　4厘米 ② 2厘米　4厘米　5厘米 ③ 2厘米　5厘米　6厘米 ④ 2厘米　6厘米　7厘米 ⑤ 3厘米　4厘米　5厘米 ⑥ 3厘米　4厘米　6厘米 ⑦ 3厘米　5厘米　6厘米 ⑧ 3厘米　5厘米　7厘米 ⑨ 3厘米　6厘米　7厘米 ⑩ 4厘米　5厘米　6厘米 ⑪4厘米　5厘米　7厘米 ⑫4厘米　6厘米　7厘米 ⑬5厘米　6厘米　7厘米