六年级数学下册回顾整理图形与几何—立体图形体积和表面积课件青岛版六三制 37页

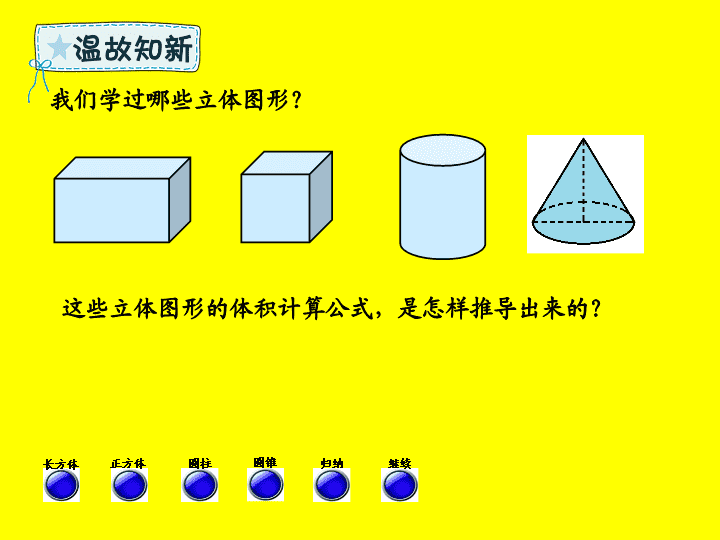
图形与几何 —— 立体图形体积和表面积 回顾整理 —— 总复习 回顾整理要求： 2 . 根据知识间的关系合理地整理； 1 . 小组合作，回忆立体图形和立体图形的知识； 3 . 把整理的结果用表格、流程图、树状图等自己喜欢的 方式表示出来。 我们学过的立体图形的体积计算公式是怎样推导出来的？它们之间有怎样的联系？ 继续 归纳 正方体 长方体 圆柱 圆锥 我们学过哪些立体图形？ 这些立体图形的体积计算公式，是怎样推导出来的？ 5 厘米 4 厘米 长方体的体积 = 长 × 宽 × 高 V = ɑbh 长方体的体积 = 底面积 × 高 V = Sh 返回 长方体体积的推导： 3 厘 米 正方体是长、宽、高都相等的长方体。 正方体的体积 = 棱长 × 棱长 × 棱长 V = ɑ 3 正方体的体积 = 底面积 × 高 V = Sh 返回 棱长 棱长 棱长 长方体的体积 = 长 × 宽 × 高 正方体体积的推导： 圆柱体体积的推导： V = S h 底面积 高 圆柱的体积 = × 长方体的体积=底面积 × 高 返回 圆锥的体积 = × 底面积 ×高 Ⅴ = Sh 1 3 圆锥的体积是等底等高的圆柱体积的 。 圆锥体体积的推导： 返回 a b h a a a h h S S V = ɑ bh V= ɑ · ɑ · ɑ = ɑ ³ V = Sh V = Sh 1 3 V = Sh S h S 返回 这些体积计算公式之间有怎样的联系呢？ 怎样选择下面的材料制作一个水桶，有几种方案？ 圆柱 长方体 水桶的形状可能是长方体的 水桶的形状可能是圆柱的 想一想，制作出的水桶可能是什么形状的？ 底面 高 底面 高 立体 平面 C = 31.4 C = 62.8 继续 31.4cm 62.8cm 底面直径： 62.8÷3.14=20 （ cm ） 返回 水桶的侧面展开图是长方形，水桶的底面是圆形 可以选择长 62.8cm 、宽 31.4cm 的长方形做水桶侧面，底面直径为 20cm 的圆做水桶的底。 62.8cm 的边作为底面周长。 20cm ② ① 62.8cm 31.4cm 62.8cm 31.4 cm 62.8 cm 31.4 cm ① 底面直径： 31.4÷3.14=10 （ cm ） 水桶的侧面展开图是长方形，水桶的底面是圆形。 可以选择长 62.8cm 、宽 31.4cm 的长方形做水桶的侧面，底面直径为 10cm 的圆做水桶的底。 31.4cm 的边作为底面周长。 返回 ③ 10 cm C =31.4 C =62.8 返回 立体 平面 62.8cm 31.4cm ① 15.7cm ④ 水桶的侧面展开图是长方形，水桶的底面是正方形。 以 62.8cm 的边作为底面周长。 正方形边长： 62.8÷4=15.7 （ cm ） 可以选择长 62.8cm 、宽 31.4cm 的长方形做水桶的侧面，边长为 15.7cm 的正方形做水桶的底。 返回 62.8cm 31.4cm ① 7.85cm ⑤ 水桶的侧面展开图是长方形，水桶的底面是正方形 长方形的宽等于底面周长 正方形边长： 31.4÷4=7.85 （ cm ） 返回 可以选择长 62.8cm 、宽 31.4cm 的长方形做水桶的侧面，边长为 7.85cm 的正方形做水桶的底。 怎样选择材料制作水桶？ 联系已有知识经验想象水桶形状 水桶的侧面展开图是长方形 水桶的底面是圆形（或正方形） 选择长方形和圆形（或正方形）材料 长方形的长或宽等于底面的周长 形成制作水桶的方案 立体 平面 立体 问题 想象 选择 计算 答案 转化图形 找出关系 推导公式 ● 我们是怎样用转化的方法推导出立体图形的体积计算公式的 ？ 长方体的体积 = 底面积 × 高 V = S h 底面积 高 圆柱的体积 = × 实验 转化 （ 1 ）长方体和正方体都有 ( 　　 ) 个面， ( 　　　 ) 条棱， ( 　　　 ) 个顶点；相对的面的面积 ( 　　　 ) ；相对的棱的长度 ( 　　　 ) 。 （ 2 ）从一个方向观察一个长方体，最多能同时看到 ( 　　 ) 个面。 1. 填空。 12 8 3 相等 6 相等 （ 3 ）一个长方体的长是 6 cm ，宽和高都是 4 cm ，那么这个长方体有 ( 　　 ) 个面是长方形。 （ 4 ）正方体是特殊的 ( 　　 　 ) 。 （ 5 ）至少要用 ( 　　 ) 个小正方体可以拼成一个大正方体。 长方体 4 8 （ 6 ）一个圆柱的上、下两个面都是 ( 　　 ) ，而且大小 ( 　　　 ) ，叫作 ( 　　 ) 面；围成圆柱的曲面叫作 ( 　　 ) 面。 （ 7 ）从圆锥的 ( 　　　 ) 到 ( 　　　　　 ) 的距离是圆锥的高。圆锥有 ( 　 ) 条高。 （ 8 ）圆柱有 ( 　 　 ) 条高，这些高都 ( 　 　 ) 。 （ 9 ）把一个圆柱沿底面直径并垂直于底面切开，会得到一个 ( 　 　　　　　 ) 形的切面。 顶点 底 无数 相等 长方形或正方 圆 侧 底面圆心 一 相等 （ 11 ） 一个正方体的棱长为 6 dm ，它的表面积是 ( ) 。 （ 12 ）一个长方体棱长总和是 48 cm ，长是 5 cm ，宽是 3 cm ，这个长方形的底面积是 ( 　　 ) ，表面积是 ( 　　 ) 。 （ 13 ）一个圆柱的底面半径是 2 厘米，高是 6 厘米，它的表面积是 ( 　　　　　　 ) 。 94 15 100.48 平方厘米 216 （ 14 ）把一个圆柱削成一个最大的圆锥，体积减少了 360 立方厘米，原来圆柱的体积是 ( 　　　 ) 立方厘米，圆锥的体积是 ( 　　　 ) 立方厘米。 （ 15 ）一个长方体的棱长总和为 2400 厘米，长、宽、高之比为 3 ∶2 ∶3 ，它的体积为 ( 　　　　 ) 立方分米，如果锯下一个最大的正方体，这个正方体的体积是 ( 　　　　 ) 立方分米。 3375 180 7593.75 540 （ 16 ）一个圆锥的体积是 9.42 ，底面直径是 6 dm ，它的高是 ( 　　 ) dm ；和它等底等高的圆柱的体积是 ( 　　　 ) 。 （ 17 ）一个圆柱形水桶的底面半径是 20 cm 、高 40 cm ，在距离桶口 5 cm 处有个缺口，这个木桶最多可装水 ( 　　　 ) 升。 28.26 43.96 1 （ 1 ） （ 2 ） （ 3 ） 2. 求下列图形的体积。 ( 单位： cm) 。 12×5×8 ＝ 480( ) 3×3×3 － 1×1×1 ＝ 26( ) (8÷2) ×3.14×10 ＝ 502.4( ) (8÷2) ×3.14×9× ＝ 150.72( ) 502.4 ＋ 150.72 ＝ 653.12( ) 6 6 6 6 9 4 6 4 3. 求立体图形的体积和表面积。（只列式不计算） 不用计算，你能很快比较出谁的体积最大吗？ 6×9×4 体积： 6×6×6 3.14× （ 4÷2 ） 2 ×6 表面积： 6×6×6 3.14×4×6+3.14 × （ 4÷2 ） 2 ×2 （ 9×4+4×6+6×9 ） × 2 一个长方体苹果箱的规格是 40×30×25 （单位： m ），它的体积是多少立方厘米？制作 10 个这样的纸箱至少需要多少板纸？ (40×30 + 40×25 +30×25) × 2 × 10 40 × 30 ×25 答：制作 10 个这样的纸箱至少需要 59000 平方厘米板纸。 4. = 1200 × 25 = 30000 （立方厘米） = 2950 ×20 = 59000 （平方厘米） 答：它的体积是 30000 立方厘米。 5. 用下面的五块玻璃做一个鱼缸，这个鱼缸的底面积是多少？ 它能装多少升水？（玻璃的厚度不计） 4.5 × 2 = 9 （平方分米） = 9×1.5 答：鱼缸的底面积是 9 平方分米，它能装 13.5 升水。 4.5×2×1.5 13.5 立方分米 = 13.5 升 = 13.5 （立方分米） 6 . 40 × 40 × 2 40cm 40cm 2cm 上升的水的体积就是不规则石块的体积。 40cm 40cm = 1600 × 2 = 3200 （立方厘米） 答：这个石块的体积是 3200 立方厘米。 一个正方体水箱，棱长是 40 厘米。如果将一个石块浸入水中，水面上升 2 厘米。这个石块的体积是多少？ 7. 瓶子里装着一些水（如下图所示），瓶底面积是 0.8 平 方分米，请你想办法计算瓶子的容积。 0.8 × 2 = 1.6 （立方分米） 0.8 × （ 3 － 2.4 ） 0.48 + 1.6 = 2.08 （立方分米） 答：瓶子的容积是 2.08 升。 = 0.8 ×0.6 = 0.48 （立方分米） 2.08 立方分米 = 2.08 升 不规则图形 规则图形 转化 40cm 40cm 2cm 40cm 40cm 想一想，刚才我们在解决这两道题时有什么共同之处？ 7. 瓶子里装着一些水（如下图所示），瓶底面积是 0.8 平 方分米，请你想办法计算瓶子的容积。 1 ．长方体的 6 个面一定都是长方形。 ( 　　 ) 2 ．用 6 张完全相同的正方形纸片可以围成一个正方体模型。 ( 　　 ) √ 辨析：长方体有六个面 , 其中四个面一定 是长方形 , 另两个面可能 是正方形。 × 判断。 3 ．圆柱上底面任意一点到下底面任意一点的距离是圆柱的高。 ( 　　 ) 4 ．把一个圆锥从顶点向底面垂直剖开，剖面一定是一个等腰三角形。 ( 　　 ) √ 辨析：上底面任意一点到下底面的 垂直距离 才是圆柱的高。 × 5 ．用 8 个相同的小正方体拼成一个大正方体，任意拿走一个小正方体后，体积、表面积一定会减少。 ( 　 ) 辨析：每个小正方体都在顶点处，每个小正方体都外露 3 个面，如果任意拿走 1 个小正方体，就会外露相同的 3 个面，所以 它的表面积与原来相比不变，而体积减少。 × 6 ．底面半径为 2 厘米的圆柱，侧面积和体积相等。 ( 　 ) 辨析：因为圆柱的 侧面积和体积是两个不同的量， 无法比较大小。 × 这节课你有哪 些收获？ 作业 请完成教材第 105 页应用与反思，第 18 、 20 、 21 、 22 、 26 、 28 题。 xx 小学 x 年级 x 班 xxx