小学数学精讲教案5_1_4_1 幻方（一） 教师版 12页

‎5-1-4‎‎-1.幻方（一）‎ 教学目标 1. 会用罗伯法填奇数阶幻方 2. 了解偶数阶幻方相关知识点 3. 深入学习三阶幻方 知识点拨 一、幻方起源 也叫纵横图，也就是把数字纵横排列成正方形，因此纵横图又叫幻方．幻方起源于我国，古人还为它编撰了一些神话．传说在大禹治水的年代，陕西的洛水经常大肆泛滥，无论怎样祭祀河神都无济于事，每年人们摆好祭品之后，河中都会爬出一只大乌龟，乌龟壳有九大块，横着数是3行，竖着数是3列，每块乌龟壳上都有几个点点，正好凑成1至9的数字，可是谁也弄不清这些小点点是什么意思．一次，大乌龟又从河里爬上来，一个看热闹的小孩惊叫起来：“瞧多有趣啊，这些点点不论横着加、竖着加还是斜着加，结果都等于十五！”于是人们赶紧把十五份祭品献给河神，说来也怪，河水果然从此不再泛滥了．这个神奇的图案叫做“幻方”，由于它有3行3列，所以叫做“三阶幻方”，这个相等的和叫做“幻和”．“洛书”就是幻和为15的三阶幻方．如下图：‎ ‎ ‎ 我国北周时期的数学家甄鸾在《算数记遗》里有一段注解：“九宫者，二四为肩，六八为足，左三右七，戴九履一，五居中央．”这段文字说明了九个数字的排列情况，可见幻方在我国历史悠久．三阶幻方又叫做九宫图，九宫图的幻方民间歌谣是这样的：“四海三山八仙洞，九龙五子一枝连；二七六郎赏月半，周围十五月团圆．”幻方的种类还很多，这节课我们将学习认识了解它们．‎ 二、幻方定义 幻方是指横行、竖列、对角线上数的和都相等的数的方阵，具有这一性质的的数阵称作三阶幻方，的数阵称作四阶幻方，的称作五阶幻方……如图为三阶幻方、四阶幻方的标准式样，‎ ‎ ‎ 三、解决这幻方常用的方法 ‎⑴适用于所有奇数阶幻方的填法有罗伯法．口诀是：一居上行正中央，后数依次右上连．上出框时往下填，右出框时往左填．排重便在下格填，右上排重一个样． ‎ ‎⑵适用于三阶幻方的三大法则有：‎ ‎①求幻和： 所有数的和÷行数（或列数）‎ ‎②求中心数：我们把幻方中对角线交点的数叫“中心数”，中心数＝幻和÷3．‎ ‎③角上的数=与它不同行、不同列、不同对角线的两数和÷2．‎ 四、数独 数独简介：（日语：数独　すうどく）是一种源自18世纪末的瑞士，后在美国发展、并在日本得以发扬光大的数学智力拼图游戏。如今数独的雏型首先于1970年代由美国的一家数学逻辑游戏杂志发表，当时名为Number Place。现今流行的数独于1984年由日本游戏杂志《パズル通信ニコリ》发表并得了现时的名称。数独本是“独立的数字”的省略，因为每一个方格都填上一个个位数。 数独可以简单的数为：让行与列及单元格的数字成规律性变换的一类数字谜问题 解题技巧：数独游戏中最常规的办法就是利用每一个空格所在的三个单元中已经出现的数字（大小数独一个空格只位于两个单元之内，但是同时多了一个大小关系作为限制条件）来缩小可选数字的范围。‎ 总结4个小技巧：‎ 1、 巧选突破口：数独中未知的空格数目很多，如何寻找突破口呢？首先我们要通过规则的限制来分析每一个空格的可选数字的个数，然后选择可选数字最少的方格开始，一般来说，我们会选择所在行、所在列和所在九宫格中已知数字比较多的方格开始，尽可能确定方格中的数字；而大小数独中已知的数字往往非常少，这个时候大小关系更加重要，我们除了利用已知数字之外更加需要考虑大小关系的限制。‎ 2、 相对不确定法：有的时候我们不能确定2个方格中的数字，却可以确定同一单元其他方格中肯定不会出现什么数字，这个就是我们说的相对不确定法。举例说明，A1可以填入1或者2，A2也可以填入1或者2，那么我们可以确定，1和2必定出现在A1和A2两者之中，A行其他位置不可能出现1或者2.‎ 3、 相对排除法：某一单元中出现好几个空格无法确定，但是我们可以通过比较这几个空格的可选数字进行对比分析来确定它们中的某一个或者几个空格。举例说明，A行中已经确定5个数字，还有4个数字（我们假设是1、2、3、4）没有填入，通过这4个空格所在的其他单元我们知道A1可以填入1、2、3、4，A2可以填入1、3，A3可以填入1、2、3，A4可以填入1、3，这个时候我们可以分析，数字4只能填入A1中，所以A1可以确定填入4，我们就可以不用考虑A1，这样就可以发现2只能填入A3中，所以A3也能确定，A2和A4可以通过其他办法进行确定。‎ 4、 假设法：如果找不到能够确定的空格，我们不妨进行假设，当然，假设也是原则的，我们不能进行无意义的假设，假设的原则是：如果通过假设一个空格的数字，可以确定和这个空格处在同一个单元内的其它某一个或者某几个空格的数字，那么我们就以选择这样的空格来假设为佳。举例说明，B3可以填入1或者2，A3可以填入2或者3，B4可以填入1或者2，这个时候我们就应该假设B3填入2，这样就可以确定A3填入3，B4填入1，然后以这个为基础进行推理，如果推出违反规则的情况出现，那么这个假设就是错误的，我们回到假设点重新开始。‎ 例题精讲 模块一、构造幻方 【例 1】 的正方形中，在每个格子里分别填入的个数字，要求每行每列及对角线上的三个数的和相等（请给出至少一种填法）．‎ ‎【考点】构造幻方 【难度】1星 【题型】填空 【解析】 方法一：第一步：求幻和：‎ 第二步：求中心数：我们把幻方中对角线交点的数叫“中心数”，仔细观察可以发现：除了对角线外，第二行、第二列也分别经过中心数，那么，经过中心数的四条线段上的数字总和是幻和的4倍，即，显然，在这个总和中，中心数用了四次，其余各数正好各用一次，所以中心数应是：‎ 第三步：确定四个角上的数．由于在同一条直线上的三个数的和是15，所以如果某格中的数是奇数，那么与这个数在同一条直线上的另两个数的奇偶性相同，所以四个角上的数必为偶数．‎ 第四步：用尝试法填一个基本解，以基本解为基础，可绕中心旋转与对调得到其它各解，共8解，下图为其中一解，其余解均可由其翻转或旋转得到：‎ 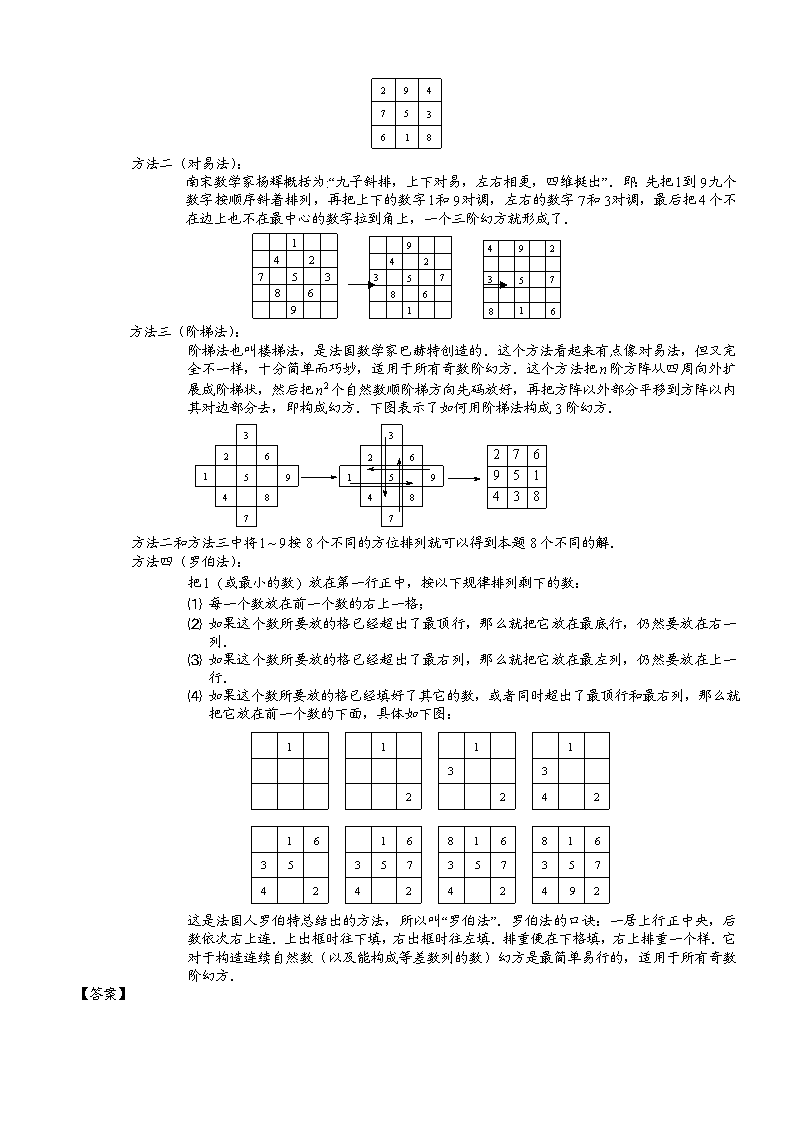方法二（对易法）：‎ 南宋数学家杨辉概括为:“九子斜排，上下对易，左右相更，四维挺出”．即：先把到九个数字按顺序斜着排列，再把上下的数字和对调，左右的数字和对调，最后把个不在边上也不在最中心的数字拉到角上，一个三阶幻方就形成了．‎ ‎ ‎ 方法三（阶梯法）：‎ 阶梯法也叫楼梯法，是法国数学家巴赫特创造的．这个方法看起来有点像对易法，但又完全不一样，十分简单而巧妙，适用于所有奇数阶幻方．这个方法把阶方阵从四周向外扩展成阶梯状，然后把个自然数顺阶梯方向先码放好，再把方阵以外部分平移到方阵以内其对边部分去，即构成幻方．下图表示了如何用阶梯法构成3阶幻方．‎ 方法二和方法三中将按8个不同的方位排列就可以得到本题8个不同的解．‎ 方法四（罗伯法）：‎ 把（或最小的数）放在第一行正中，按以下规律排列剩下的数：‎ ‎⑴ 每一个数放在前一个数的右上一格；‎ ‎⑵ 如果这个数所要放的格已经超出了最顶行，那么就把它放在最底行，仍然要放在右一列．‎ ‎⑶ 如果这个数所要放的格已经超出了最右列，那么就把它放在最左列，仍然要放在上一行．‎ ‎⑷ 如果这个数所要放的格已经填好了其它的数，或者同时超出了最顶行和最右列，那么就把它放在前一个数的下面，具体如下图：‎ 这是法国人罗伯特总结出的方法，所以叫“罗伯法”．罗伯法的口诀：一居上行正中央，后数依次右上连．上出框时往下填，右出框时往左填．排重便在下格填，右上排重一个样．它对于构造连续自然数（以及能构成等差数列的数）幻方是最简单易行的，适用于所有奇数阶幻方．‎ ‎【答案】‎ 【例 1】 的正方形格子中，在每个格子里分别填入的个数字，要求每行每列及对角线上的三个数的和相等（请给出至少一种填法）．‎ ‎【考点】构造幻方 【难度】2星 【题型】填空 【解析】 第一步：求幻和：．‎ 第二步：求中心数：我们把幻方中对角线交点的数叫“中心数”，仔细观察可以发现：除了对角线外，第二行、第二列也分别经过中心数，那么，经过中心数的四条线段上的数字总和是幻和的4倍，即，显然，在这个总和中，中心数用了四次，其余各数正好各用一次，所以中心数应是：．‎ 第三步：确定四个角上的数：用尝试法，不难推知，四个角只能是奇数．‎ 第四步：用尝试法填一个基本解，以基本解为基础，可绕中心旋转与对调得到其它各解，共8解．下图为其中一解，其余解均可由其翻转或旋转得到：‎ 其他方法这里不再做介绍，同学们可以自己尝试练习．　　　　　‎ ‎【答案】‎ 【例 2】 用11，13，15，17，19，21，23，25，27编制成一个三阶幻方。‎ ‎【考点】构造幻方 【难度】2星 【题型】填空 ‎ 【解析】 方法一：给出的九个数形成一个等差数列，1～9也是一个等差数列．不难发现：中间方格里的数 字应填等差数列的中间数，也就是第五个数，即应填19；填在四个角上方格中的数是位 于偶数项的数，即13，17，21，25，而且对角两数的和相等，即；余下 各数就不难填写了(见下图)．‎ ‎　　 与幻方相反的问题是反幻方．将九个数填入(三行三列)的九个方格中，使得任一行、任一列以及两条对角线上的三个数之和互不相同，这样填好后的图称为三阶反幻方．‎ ‎ 方法二：用阶梯法，在三阶幻方的上下左右的中间添加一格，先将数字按从小到大的顺序，以斜行方向从左下向右上依次填写，再把添加格内的数填到本行(或本列)中相隔两行(或两列)的方格中．‎ ‎ 方法三：对易法：九子斜排，上下对易，左右相更，四维挺出．‎ ‎ 方法四：用罗伯法的口诀：一居上行正中央，后数依次右上连．上出框时往下填，右出框时往左填．排重便在下格填，右上排重一个样．‎ ‎【答案】‎ 【例 1】 如下图的的阵列中填入了的自然数，构成大家熟知的3阶幻方．现在另有一个 的阵列，请选择9个不同自然数填入9个方格中，使得其中最大者为20，最小者大于5，且要求横加、竖加、对角线方式相加的3个数之和都相等．‎ ‎ ‎ ‎【考点】构造幻方 【难度】3星 【题型】填空 ‎ 【解析】 观察原表中的各数是从1～9不同的九个自然数，其中最大的数是9，最小的数是1，且横加、竖加、对角线方式相加结果相等．根据题意，要求新制的幻方最大数为20，而，因此，如果原表中的各数都增加11，就能符合新表中的条件了．如下图．‎ ‎【答案】‎ 【例 2】 从1、2、3…20这20个数中选出9个不同的数放入3×3的方格表中，使得每行、每列、每条对角线上的三个数的和都相等。这个9个数中最多有_______个质数。‎ ‎【考点】幻方性质 【难度】4星 【题型】解答 ‎【关键词】走美杯，四年级，初赛，第4题 【解析】 最多有7个质数 ‎【答案】‎ 【例 3】 请你将这二十五个自然数填入的空格内使每行、每列、每条对角线上的五数之和相等．‎ ‎【考点】构造幻方 【难度】2星 【题型】填空 【解析】 ‎①罗伯法：教师边写边说口诀：“一居上行正中央，后数依次右上连．上出框时往下填，右出框 时往左填．排重便在下格填，右上排重一个样”．见第二个图．这是法国人罗伯特总结出的“罗伯法”，它对于构造连续自然数（以及能构成等差数列的数）幻方是最简单易行的，适用于所有奇数阶幻方． ‎ ‎②阶梯法：阶梯法也叫楼梯法，是法国数学家巴赫特创造的．这个方法十分简单而巧妙，适用于所有奇数阶幻方．这个方法把阶方阵从四周向外扩展成阶梯状，然后把个自然数顺阶梯方向先码放好，再把方阵以外部分平移到方阵以内其对边部分去，即构成幻方．下面的图⑴和图⑵表示了如何用阶梯法构成5阶幻方．图⑴中顶边以上的4、5、10三个数在图⑵中被移入底边上方相应的3个原先为空的方格中，其余三侧照此处理．‎ ‎ ‎ ‎ ⑴ ⑵‎ ‎⑵练习：大家一起来练习用罗伯法写个七阶的幻方，注意强调细节．上出框与右出框的处理有时不容易把握，老师隆重推荐大家一种方法——“卷纸筒”，即把上下边重合在一线，则上出框后往右上填的位置正好在下边的对应点上．强调这种方法适用于任意奇数阶幻方．‎ ‎【答案】‎ 模块二、幻方性质 【例 1】 将九个数填入下图的九个空格中，使得任一行、任一列以及两条对角线上的三个数之和都等于定数，则中心方格中的数必为．‎ ‎ ‎ ‎【考点】幻方性质 【难度】4星 【题型】解答 【解析】 略 ‎【答案】因为每行的三数之和都等于，共有三行，所以九个数之和等于．如右上图所示，经过中心方格的有四条虚线，每条虚线上的三个数之和都等于k，四条虚线上的所有数之和等于，其中只有中心方格中的数是“重叠数”，九个数各被计算一次后，它又被重复计算了三次．所以有：‎ ‎　　 九数之和+中心方格中的数，‎ ‎　　 中心方格中的数，‎ ‎　　 中心方格的数 ‎　　 注意：例题中对九个数及定数都没有特殊要求．这个结论对求解方格中的数阵问题很实用．‎ 【例 2】 请编出一个三阶幻方，使其幻和为24．‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎ 【解析】 ‎⑴根据题意，要求其三阶幻方的幻和为24，所以中心数为．‎ ‎⑵既然8是中心数，那么与8在一条直线的各个组的其余两数的和为16，想一想哪两个数相加为16呢？，，，，，，‎ ‎　　 ⑶按上述条件进行估算后填出，然后再进行调整即可得正确的答案．‎ ‎　‎ ‎【答案】‎ 【巩固】 将九个连续自然数填入下图的九个空格，使每一横行及每一竖列的三个数之和都等于60．‎ ‎ ‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎ 【解析】 介绍三阶幻方时，我们已经知道了的填法及各行各列三个数相加的和均为15，现在要求每一横行及每一竖列的三个数之和为60，显然每个数增加就可以了．右上图为其中一个解．‎ ‎【答案】‎ 【例 1】 将九个数填入下图的空格中，使得每行、每列以及每条对角线上的三个数之和都相等，证明：‎ ‎【考点】幻方性质 【难度】4星 【题型】解答 【解析】 略 ‎【答案】设中心数为(如上图)，因此每行、每列以及每条对角线上的三个数之和都等于，第一行中间的数为，右下角的数为．根据第一行和第三列可求出右上图中*的数，由此可得：‎ 所以 【例 2】 在下图中的、、、处填上适当的数，使下图成为一个三阶幻方．‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎ 【解析】 ‎⑴ 从1行和3列得：，，．‎ ‎⑵ 观察对角线上的三个数的总和，实际上它即为每行、每列的三个数的和．对角线上的三个数的和：．‎ ‎　　 ⑶ ．‎ ‎　　 ⑷ ．‎ ‎　　 ⑸ ．∴、、、．‎ ‎【答案】、、、‎ 【巩固】 在图的九个方格里，每行、每列、每条对角线上的三个数的和都相等，则N= 。‎ ‎【考点】幻方性质 【难度】2星 【题型】填空 ‎【关键词】希望杯，四年级，复赛，第9题，5分 【解析】 ‎【答案】‎ 【巩固】 在下面两幅图的每个空格中，填入7个自然数，使得每行、每列、每条对角线上的三个数之和等于21．‎ ‎ ‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎ 【解析】 根据题意填法如下：‎ ‎【答案】‎ 【巩固】 在图1所示的和方格表中填入合适的数,使得每行、每列以及每条对角线上的三个数的和相等。那么标有“★”的方格内应填入的数是_______.‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎【关键词】希望杯，六年级，初赛，第4题，6分 【解析】 ‎【答案】‎ 【例 1】 在九宫图中，第一行第三列的位置上填5，第二行第一列位置上填6，如下图．请你在其他方格中填上适当的数，使方阵横、纵、斜三个方向的三个数之和均为27．‎ ‎ ‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎ 【解析】 为了叙述方便，我们将其余方格用字母表示，如上右图所示．根据题意可知：‎ ‎　　 (1)‎ ‎　　 (2)‎ ‎　　 (3)‎ ‎　　 (4)‎ ‎　　 (5)‎ ‎　　 (6)‎ ‎　　 (7)‎ ‎　　 (8)‎ ‎　　 由中心数幻和得知：．‎ ‎　　 将代入(4)，得，将代入(2)，则．‎ ‎　　 将代入(3)，则．将代入(5)，则．将代入(1)，则．　将、代入(7)，则．‎ 由分析可知，中心方格必须填数字9，其他方格中也只有一种填法．见右上图．‎ ‎【答案】‎ 【巩固】 在下图的空格里填入七个自然数，使每一行、每一列及每一条对角线上的上的三个数的和都等于90．‎ ‎ ‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎ 【解析】 中心数，又由知第一行第三列的数为，由知第一行第二列的数是；第一行第一列的数是；第二行第三列的数是；第三行第一列的数是；第三行第三列的数是，所以答案见右上图．‎ ‎【答案】‎ 【巩固】 右图中有九个空格，要求每个格中填入互不相同的数，使得每行、每列、每条对角线上的三个数之和都相等。问：图中左上角的数是多少?‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎【关键词】华杯赛，初赛，第9题 【解析】 如图，设相应方格中的数为x1，x2，x3，x4。‎ 由已知条件：行、列及对角线的三个数的和都相等，可以列出下面的等式(方程)：?十x1十x2＝?＋x3＋x4＝x1＋x3＋13＝x2十19＋x4，这样，前面两个式子的和就等于后面两个式子的和，即有2×？＋x1十x2＋x3＋x4＝13＋19＋x1十x2＋x3＋x4所以2×?＝13＋19 ？＝＝16，左上角的数是16‎ ‎【答案】‎ 【巩固】 图中是一个幻方，满足每行、每列及两条对角线上三数之和都相等，那么其中“★”代表的数是__________．‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎【关键词】学而思杯，4年级，第11题 【解析】 总和为★，左下角应该是16，中间应该是★=(10+16)÷2=13，所以★‎ ‎【答案】‎ 【巩固】 图中______,______,______，______时，它才能构成一个三阶幻方？‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎ 【解析】 从第一列第三行可知,．又由两条对角线可知,得．再由每行和可知，由此，其余各数都可求得，即,,,‎ ‎【答案】,,,‎ 【巩固】 在如图所示的九宫图中，不同的汉字代表不同的数，每行、每列和两条对角线上各数的和相等。已知中＝21，学＝9，欢＝12，则希，望，杯的和是__________ 。‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎【关键词】希望杯，六年级，二试，第10题，5分 【解析】 可通过设未知数填出整个幻方，希望杯的和为54。‎ ‎【答案】‎ 【例 1】 在下面的方格中填入0～9中的数字，使得每行每列的和等于每行的右端及每列的下端所写的数字．其中，所有的0都已经填好，而且同一行或者同一列中不允许出现相同的非零数字．则对角线上的四个数字所组成的四位数是 ．‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎【关键词】学而思杯，5年级，第9题 【解析】 突破口在D，横看D的结果可以是3也可以是1，但是竖看D若为1D上面的空格为11，不符合方格中填0～9中数字，所以D为3，依次类推出A为1，所以答案为1963‎ ‎【答案】‎ 【巩固】 方格中的图形符号“◇”，“○”，“▽”，“☆”代表填入方格中的数，相同的符号代表相同的数，如图所示，若第一列，第三列，第二行，第四行的四个数的和分别是36，50，41，37，则第三行的四个数的和为 ‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎ ‎【关键词】华杯赛，决赛，第7题，10分 【解析】 ‎：根据题意知道，解得，所以题目要求的第三行结果为 ‎【答案】‎ 【例 2】 将2、4、6、8、12、18、24、36、72填入右边的九宫格， 使每行每列及两条对角线上三数的积都相等．每行的三个数的积是______．‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎ ‎【关键词】走美杯，初赛，六年级，第3题 【解析】 每行三个数的积相等，所以这个积的3次方等于9个数的积，这九个数是：2130、2230、2131、2330、2231、2132、2331、2232、2332，它们的积21839，所以每行上的3个数的积为2633=1728.‎ ‎【答案】‎ 【例 3】 请将1～9这9个数填入右图3×3表格中，使得第1,2行三数的乘积分别是70，24，第l,2列三数的乘积分别是 21．72．‎ ‎ ‎ ‎【考点】幻方性质 【难度】3星 【题型】填空 ‎ ‎【关键词】走美杯，五年级，初赛，第3题 【解析】 因为70=2×5×7， 21=1×3×7，所以A=7，D等于2或5，因为D×E×F=72，72不能被5整除，所以D为2，72=2×4×9,即E为4或9，且B×E×H=24。24不能被9整除，所以E为4，24=1×4×6，也就是B=1，H=6，剩下的数易得。最后结果为：‎ ‎【答案】‎