小学数学精讲教案4_3_1 三角形等高模型与鸟头模型（一） 学生版 26页

‎4-3-1.三角形等高模型与鸟头模型 例题精讲 板块一 三角形等高模型 我们已经知道三角形面积的计算公式：三角形面积底高 从这个公式我们可以发现：三角形面积的大小，取决于三角形底和高的乘积．‎ 如果三角形的底不变，高越大(小)，三角形面积也就越大(小)；‎ 如果三角形的高不变，底越大(小)，三角形面积也就越大(小)；‎ 这说明当三角形的面积变化时，它的底和高之中至少有一个要发生变化．但是，当三角形的底和高同时发生变化时，三角形的面积不一定变化．比如当高变为原来的3倍，底变为原来的，则三角形面积与原来的一样．这就是说：一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化．同时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状．‎ 在实际问题的研究中，我们还会常常用到以下结论：‎ ‎①等底等高的两个三角形面积相等；‎ ‎②两个三角形高相等，面积比等于它们的底之比；‎ 两个三角形底相等，面积比等于它们的高之比；‎ 如左图 ‎ ‎ ‎③夹在一组平行线之间的等积变形，如右上图；‎ 反之，如果，则可知直线平行于．‎ ‎④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)；‎ ‎⑤三角形面积等于与它等底等高的平行四边形面积的一半；‎ ‎⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．‎ 【例 1】 你有多少种方法将任意一个三角形分成：⑴ 3个面积相等的三角形；⑵ 4个面积相等的三角形；⑶6个面积相等的三角形．‎ ‎ ‎ ‎ ‎ 【例 2】 如图，BD长‎12厘米，DC长‎4厘米，B、C和D在同一条直线上．‎ ‎⑴ 求三角形ABC的面积是三角形ABD面积的多少倍？‎ ‎⑵ 求三角形ABD的面积是三角形ADC面积的多少倍？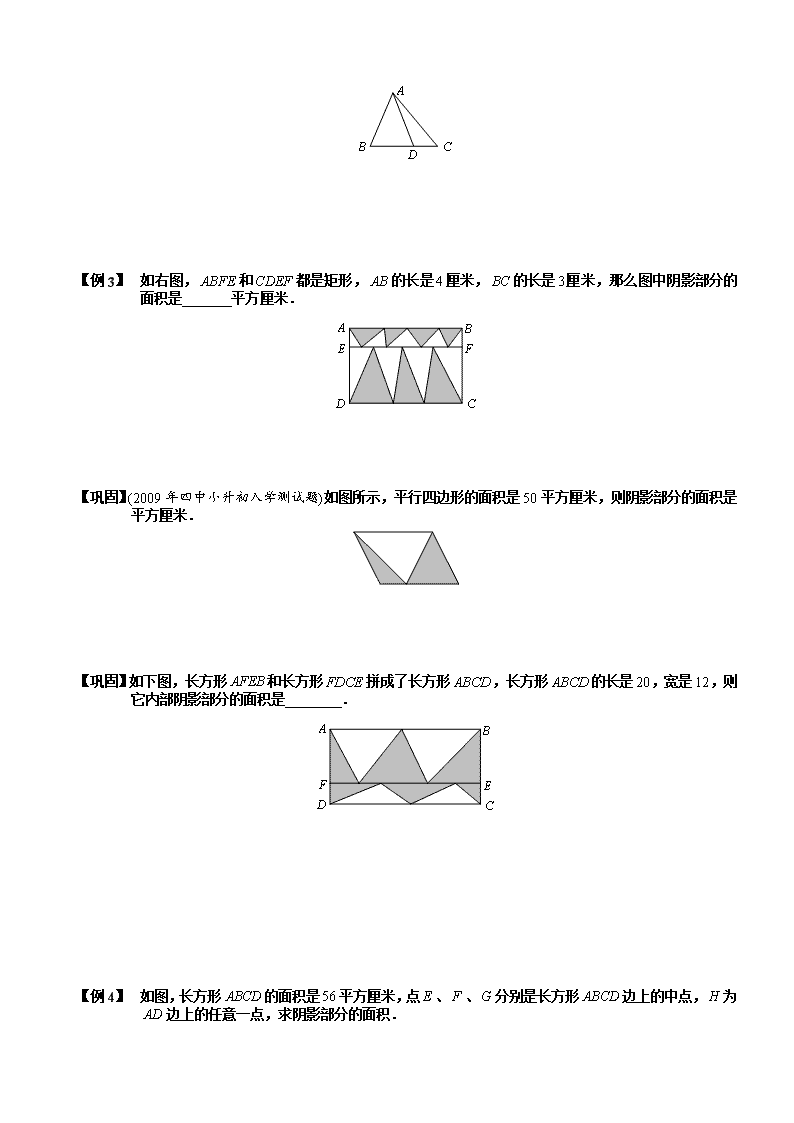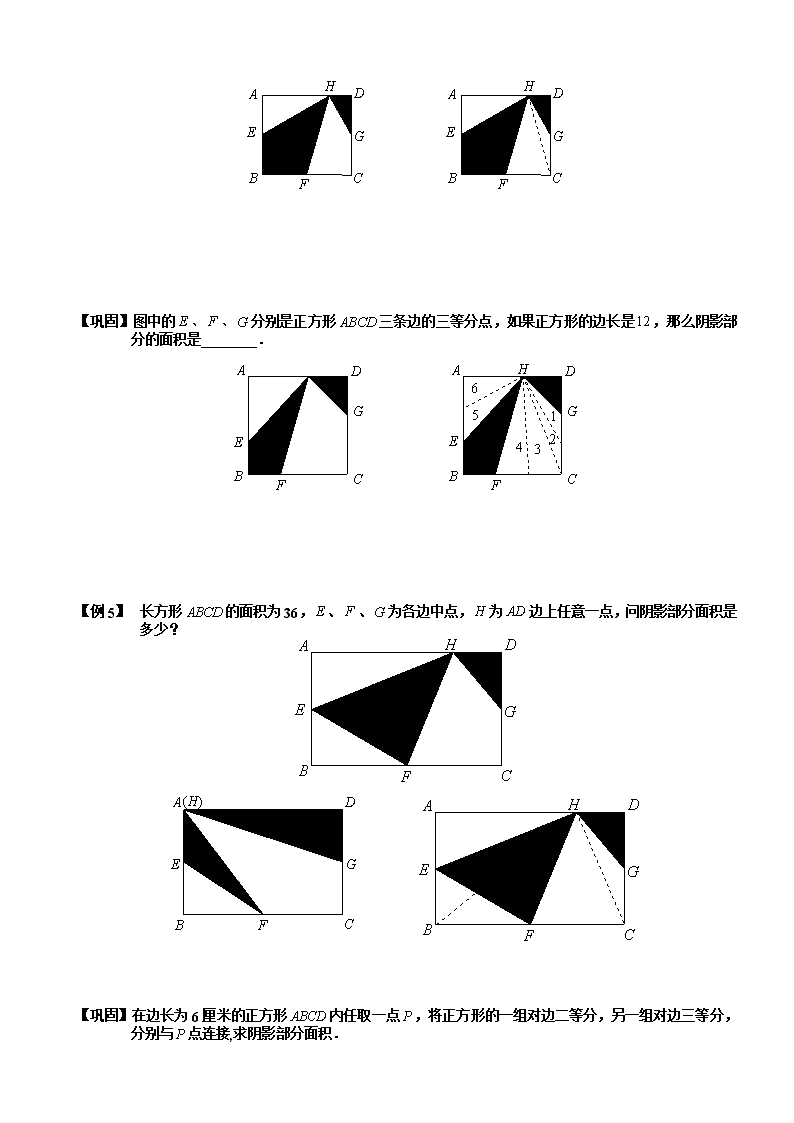‎ 【例 1】 如右图，和都是矩形，的长是厘米，的长是厘米，那么图中阴影部分的面积是 平方厘米．‎ ‎【巩固】(2009年四中小升初入学测试题)如图所示，平行四边形的面积是50平方厘米，则阴影部分的面积是 平方厘米．‎ ‎【巩固】如下图，长方形和长方形拼成了长方形，长方形的长是20，宽是12，则它内部阴影部分的面积是 ．‎ 【例 2】 如图，长方形的面积是平方厘米，点、、分别是长方形边上的中点，为边上的任意一点，求阴影部分的面积．‎ ‎ ‎ ‎【巩固】图中的、、分别是正方形三条边的三等分点，如果正方形的边长是，那么阴影部分的面积是 ．‎ ‎ ‎ 【例 1】 长方形的面积为36，、、为各边中点，为边上任意一点，问阴影部分面积是多少？‎ ‎ ‎ ‎【巩固】在边长为‎6厘米的正方形内任取一点，将正方形的一组对边二等分，另一组对边三等分，分别与点连接,求阴影部分面积．‎ ‎ ‎ 【例 1】 如右图，E在AD上，AD垂直BC，厘米，厘米．求三角形ABC的面积是三角形EBC面积的几倍？‎ 【例 2】 如图，在平行四边形ABCD中，EF平行AC，连结BE、AE、CF、BF那么与BEC等积的三角形一共有哪几个三角形？‎ ‎【巩固】如图，在ABC中，D是BC中点，E是AD中点，连结BE、CE，那么与ABE等积的三角形一共有哪几个三角形？‎ ‎【巩固】如图，在梯形ABCD中，共有八个三角形，其中面积相等的三角形共有哪几对？‎ 【例 1】 如图，三角形的面积为1，其中，，三角形 的面积是多少？‎ 【例 2】 如右图，，，已知阴影部分面积为5平方厘米，的面积是 平方厘米．‎ ‎ ‎ ‎【巩固】图中三角形的面积是180平方厘米，是的中点，的长是长的3倍，的长是 长的3倍．那么三角形的面积是多少平方厘米？ ‎ ‎【巩固】如图，在长方形中，是的中点，是的中点，如果厘米，厘米，求三角形的面积．‎ ‎【巩固】如图，三角形ABC的面积是24，D、E和F分别是BC、AC和AD的中点．求三角形DEF的面积．‎ ‎【巩固】如图，在三角形ABC中，厘米，高是‎6厘米，E、F分别为AB和AC的中点，那么三角形EBF的面积是多少平方厘米？‎ 【例 1】 如图所示，、、都是正方形边的中点，△比△大平方厘米。△的面积为 平方厘米。‎ 【例 2】 如图ABCD是一个长方形，点E、F和G分别是它们所在边的中点．如果长方形的面积是36‎ 个平方单位，求三角形EFG的面积是多少个平方单位．‎ ‎ ‎ ‎【巩固】如图，长方形的面积是，是边的中点，在边上，且.那么，阴影部分的面积是多少？‎ 【例 1】 如图，大长方形由面积是12平方厘米、24平方厘米、36平方厘米、48平方厘米的四个小长方形组合而成．求阴影部分的面积．‎ ‎ ‎ 【例 2】 图中ABCD是个直角梯形(∠DAB=∠ABC=90°)，以AD为一边向外作长方形ADEF，其面积为6.36平方厘米。连接BE交AD于P，再连接PC。则图中阴影部分的面积是( )平方厘米。‎ ‎(A)6.36　　(B)3.18　　 (C)2.12　　（D）1.59‎ 【例 3】 如图，是半径为的圆上的弦，且的长度与圆的半径相等，是圆外的一点，的长度为，且与 平行，那么图中阴影部分的面积是 。（）‎ ‎【巩固】在下图中，A为半径为3的⊙0外一点。弦BC∥A0且BC=3。连结AC。阴影面积等于 .(=3.14)‎ 【例 1】 如图，三角形中，，，三角形ADE的面积是20平方厘米，三角形的面积是多少？‎ 【例 2】 如图，在三角形中，已知三角形、三角形、三角形的面积分别是89，28，26．那么三角形的面积是 ．‎ 【例 3】 如图，梯形ABCD被它的一条对角线BD分成了两部分．三角形BDC的面积比三角形ABD的面积大10平方分米．已知梯形的上底与下底的长度之和是15分米，它们的差是5分米．求梯形ABCD的面积．‎ ‎ ‎ 【例 1】 图中AOB的面积为，线段OB的长度为OD的3倍，求梯形ABCD的面积．‎ 【例 2】 如图，把四边形ABCD改成一个等积的三角形．‎ ‎　　　　　　　　　　‎ 【例 3】 一个长方形分成4个不同的三角形，绿色三角形面积占长方形面积的，黄色三角形面积是．问：长方形的面积是多少平方厘米？‎ 【例 4】 是长方形内一点，已知的面积是，的面积是，求的面积是多少？‎ 【例 1】 如右图，过平行四边形内的一点作边的平行线、，若的面积为8平方分米，求平行四边形的面积比平行四边形的面积大多少平方分米？‎ ‎ ‎ 【例 2】 如右图，正方形的面积是，正三角形的面积是，求阴影的面积．‎ ‎ ‎ ‎【巩固】如右图，正方形的面积是，正三角形的面积是，求阴影的面积．‎ ‎ ‎ 【例 3】 在长方形内部有一点，形成等腰的面积为16，等腰的面积占长方形面积的，那么阴影的面积是多少？‎ 【例 1】 如右图所示，在梯形中，、分别是其两腰、的中点，是上的任意一点，已知 的面积为，而的面积恰好是梯形面积的，则梯形的面积是 ．‎ ‎ ‎ 【例 2】 如图所示，四边形与都是平行四边形，请你证明它们的面积相等．‎ ‎ ‎ ‎【巩固】如图所示，正方形的边长为厘米，长方形的长为厘米，那么长方形的宽为几厘米？‎ ‎ ‎ 【例 3】 如图，正方形ABCD的边长为6，AE＝1.5，CF＝2．长方形EFGH的面积为 ．‎ 【例 1】 如图，ABCD为平行四边形，EF平行AC，如果ADE的面积为4平方厘米．求三角形CDF的面积．‎ ‎ 　　 ‎ ‎【巩固】如右图，在平行四边形中，直线交于，交延长线于，若，求 的面积．‎ ‎ ‎ 【例 2】 梯形ABCD中，AE与DC平行，, .‎ 【例 3】 图中两个正方形的边长分别是‎6厘米和‎4厘米，则图中阴影部分三角形的面积是多少平方厘米．‎ 【例 1】 如图，有三个正方形的顶点、、恰好在同一条直线上，其中正方形的边长为‎10厘米，求阴影部分的面积．‎ ‎【巩固】右图是由大、小两个正方形组成的，小正方形的边长是厘米，求三角形的面积．‎ ‎ ‎ ‎【巩固】如图，与均为正方形，三角形的面积为6平方厘米，图中阴影部分的面积为 ．‎ ‎ ‎ ‎【巩固】正方形ABCD和正方形CEFG，且正方形ABCD边长为‎10厘米，则图中阴影面积为多少平方厘米？‎ ‎ ‎ ‎【巩固】已知正方形边长为10，正方形边长为6，求阴影部分的面积．‎ ‎ ‎ 【例 1】 于的三分之一，三角形的面积等于6平方厘米，求五边形的面积．‎ ‎ ‎ 【例 2】 如下图，、分别是梯形的下底和腰上的点，，并且甲、乙、丙个三角形面积相等．已知梯形的面积是平方厘米．求图中阴影部分的面积．‎ 【例 3】 如图，已知长方形的面积，三角形的面积是，三角形的面积是，那么三角形 的面积是多少？‎ ‎ ‎ 【例 1】 如图，在平行四边形中，，．求阴影面积与空白面积的比．‎ 【例 2】 如图所示，三角形中，是边的中点，是边上的一点，且，为与的交点．若的面积为平方厘米，的面积为平方厘米．且是平方厘米，那么三角形的面积是 平方厘米．‎ 【例 3】 如图，在梯形中，，，且的面积比的面积小10平方厘米．梯形的面积是 平方厘米．‎ ‎【巩固】如图，是梯形的一条对角线，线段与平行， 与相交于点．已知三角形 的面积比三角形的面积大平方米，并且．求梯形的面积．‎ ‎ ‎ 【例 1】 如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是，，．那么图中阴影部分的面积是多少？‎ 【例 2】 图中是一个各条边分别为‎5厘米、‎12厘米、‎13厘米的直角三角形．将它的短直角边对折到斜边上去与斜边相重合，那么图中的阴影部分(即未被盖住的部分)的面积是多少平方厘米？‎ ‎ ‎ 【例 3】 如图，长方形的面积是2平方厘米，，是的中点．阴影部分的面积是多少平方厘米？‎ 【例 4】 如图，三角形田地中有两条小路和，交叉处为，张大伯常走这两条小路，他知道,且 ‎．则两块地和的面积比是_________．‎ 【例 1】 如图，，，被分成个面积相等的小三角形，那么 ．‎ ‎【巩固】如图，在角的两边上分别有、、及、、六个点，并且、、、、的面积都等于1，则的面积等于 ．‎ 【例 2】 ‎、分别为直角梯形两边上的点，且、、彼此平行，若，，，．求阴影部分的面积．‎ ‎ ‎ 【例 3】 已知为等边三角形，面积为400，、、分别为三边的中点，已知甲、乙、丙面积和为143‎ ‎，求阴影五边形的面积．(丙是三角形)‎ 【例 1】 如图，已知，，，，线段将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形的面积是 ．‎ ‎ ‎ ‎【巩固】如图，点、、在线段上，已知厘米，厘米，厘米，厘米，将整个图形分成上下两部分，下边部分面积是平方厘米，上边部分面积是平方厘米，则三角形的面积是多少平方厘米？‎ 【例 2】 如图，正方形的边长为10，四边形的面积为5，那么阴影部分的面积是 ．‎ ‎ ‎ ‎【巩固】如图，正方形的边长为12，阴影部分的面积为60，那么四边形的面积是 ．‎ ‎ ‎ 【例 1】 如图所示，长方形内的阴影部分的面积之和为70，，，四边形的面积为 ．‎ ‎【巩固】如图所示，矩形的面积为24平方厘米．三角形与三角形 的面积之和为平方厘米，则四边形的面积是 平方厘米．‎ ‎【巩固】如图所示，矩形的面积为36平方厘米，四边形的面积是3‎ 平方厘米，则阴影部分的面积是 平方厘米．‎ ‎【巩固】如图，长方形的面积是36，是的三等分点，，则阴影部分的面积为 ．‎ ‎ ‎ 【例 1】 如图，如果长方形的面积是平方厘米，那么四边形的面积是多少平方厘米？‎ ‎ ‎ 【例 2】 如图，阴影部分四边形的外接图形是边长为的正方形，则阴影部分四边形的面积是 ．‎ ‎ ‎ ‎【巩固】如图，阴影部分四边形的外接图形是边长为 厘米的正方形，则阴影部分四边形的面积是多少平方厘米？‎ ‎ ‎ ‎【巩固】已知正方形的边长为10，，，则 ．‎ ‎ ‎ 【例 1】 如图，三角形的面积是，、的长度分别为11、3．求长方形的面积．‎ ‎ ‎ 【例 2】 如图，长方形中，，．、分别是边上的两点，．那么，三角形面积的最小值是 ．‎ ‎ ‎ 【例 3】 是边长为12的正方形，如图所示，是内部任意一点，、‎ ‎，那么阴影部分的面积是 ．‎ ‎ ‎ 【例 1】 如图所示，在四边形中，，，，分别是各边的中点，求阴影部分与四边形的面积之比．‎ ‎ ‎ ‎【巩固】如图，、、、分别是四边形各边的中点，与交于点，、、及分别表示四个小四边形的面积．试比较与的大小．‎ ‎ ‎ 【例 2】 如图，四边形中，，，，已知四边形的面积等于4，则四边形的面积 ．‎ ‎ ‎ ‎【拓展】如图，对于任意四边形，通过各边三等分点的相应连线，得到中间四边形，求四边形的面积是四边形的几分之几？‎ 【例 1】 有正三角形，在边、、的正中间分别取点、、，在边、、上分别取点、、，使，当和、和、和的相交点分别是、、时，使．这时，三角形的面积是三角形的面积的几分之几？请写出思考过程．‎ 【例 2】 如图：已知在梯形中，上底是下底的，其中是边上任意一点，三角形、三角形、三角形的面积分别为、、．求三角形的面积．‎ ‎ ‎ 【例 1】 如图，已知是梯形，∥，，，，求的面积．‎ ‎ ‎ 【例 2】 如图，是一个四边形，、分别是、的中点．如果、与的面积分别是6、7和8，且图中所有三角形的面积均为整数，则四边形的面积为 ．‎ ‎ ‎ 【例 3】 直角边长分别为‎18厘米,‎10厘米的直角△ABC和直角边长分别为‎14厘米,‎4厘米的直角△ADE如图摆放．M为AE的中点，则△ACM的面积为 平方厘米．‎ ‎ ‎ 【例 1】 如右图，过平行四边形内的一点作边的平行线、，若的面积为6，求平行四边形的面积比平行四边形的面积大 ．‎ 【例 2】 如图，平行四边形ABCD与平行四边形EFCG是两个形状一模一样的平行四边形，点G、D、都在线段AE上，三角形BEF的面积是2，那么三角形ABD的面积是____.‎ 【例 3】 如图长方形ABCD，AB = 24，BC = 18，把AB边对折到AC上与AC重合，把AD边也对折到AC上与AC重合，请问得到的新图形的面积是多少？‎