小学数学精讲教案4_3_5 任意四边形、梯形与相似模型（三） 学生版 13页

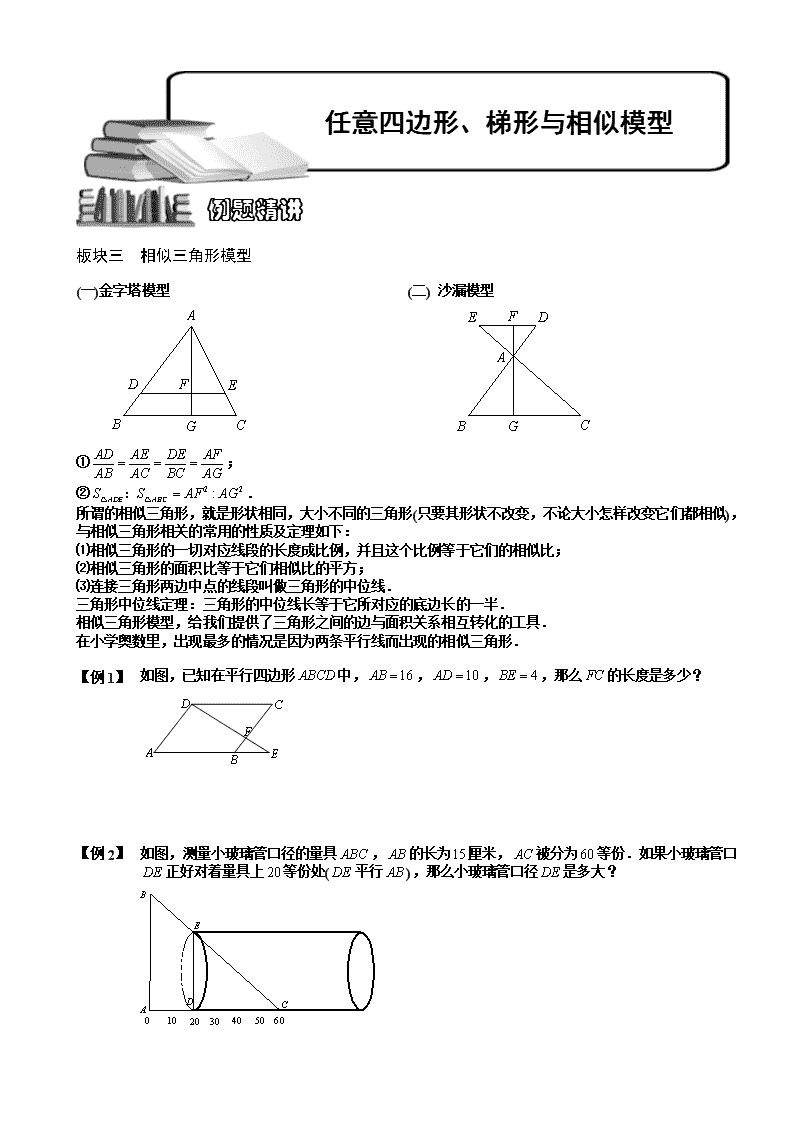
任意四边形、梯形与相似模型 例题精讲 板块三 相似三角形模型 ‎(一)金字塔模型 (二) 沙漏模型 ‎ ‎ ‎①；‎ ‎②．‎ 所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：‎ ‎⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比；‎ ‎⑵相似三角形的面积比等于它们相似比的平方；‎ ‎⑶连接三角形两边中点的线段叫做三角形的中位线．‎ 三角形中位线定理：三角形的中位线长等于它所对应的底边长的一半．‎ 相似三角形模型，给我们提供了三角形之间的边与面积关系相互转化的工具．‎ 在小学奥数里，出现最多的情况是因为两条平行线而出现的相似三角形．‎ 【例 1】 如图，已知在平行四边形中，，，，那么的长度是多少？‎ 【例 2】 如图，测量小玻璃管口径的量具，的长为厘米，被分为等份．如果小玻璃管口正好对着量具上等份处(平行)，那么小玻璃管口径是多大？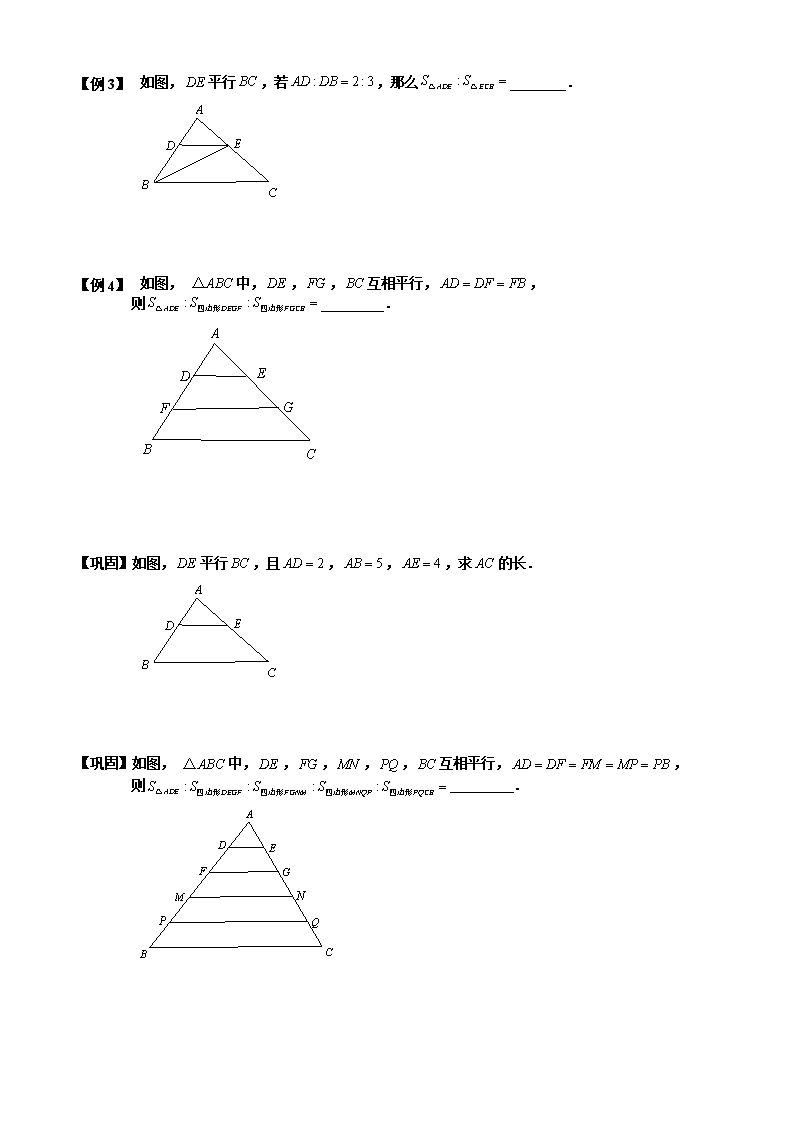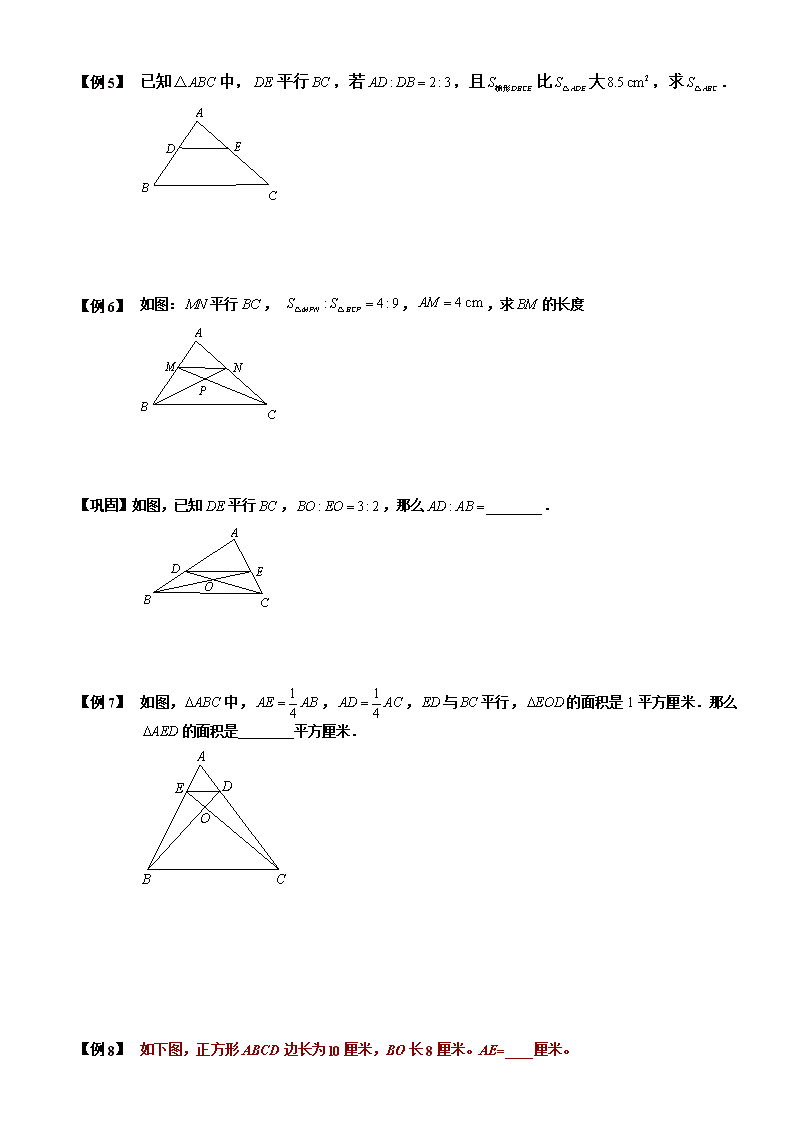 ‎ 【例 1】 如图，平行，若，那么________．‎ 【例 2】 如图， 中，，，互相平行，，‎ 则 ．‎ ‎【巩固】如图，平行，且，，，求的长．‎ ‎【巩固】如图， 中，，，，，互相平行，，‎ 则 ．‎ 【例 1】 已知中，平行，若，且比大，求．‎ 【例 2】 如图：平行， ，，求的长度 ‎【巩固】如图，已知平行，，那么________．‎ 【例 3】 如图，中，，，与平行，的面积是1平方厘米．那么的面积是 平方厘米．‎ 【例 4】 如下图，正方形ABCD边长为l‎0厘米，BO长‎8厘米。AE=____厘米。‎ 【例 1】 如图，已知正方形ABCD的边长是12厘米，E是CD边上的中点，连接对角线AC，交BE于点O，则三角形AOB的面积是（ ）平方厘米。‎ A、24 B、‎36 ‎‎ C、48 D、60‎ 【例 2】 在图中的正方形中，，，分别是所在边的中点，的面积是面积的几倍？‎ ‎ ‎ 【例 3】 图30-10是一个正方形，其中所标数值的单位是厘米．问：阴影部分的面积是多少平方厘米?‎ 【例 4】 如图，线段与垂直，已知，，那么图中阴影部分面积是多少？‎ ‎ ‎ 【例 1】 如图，四边形和都是平行四边形，四边形的面积是，，则四边形的面积________．‎ 【例 2】 已知三角形的面积为，，是的中点，且∥，交于，求阴影部分的面积．‎ ‎ ‎ 【例 3】 已知正方形，过的直线分别交、的延长线于点、，且，，求正方形的边长．‎ 【例 4】 如图，三角形是一块锐角三角形余料，边毫米，高毫米，‎ 要把它加工成正方形零件，使正方形的一边在上，其余两个顶点分别在、上，这个正方形零件的边长是多少？‎ ‎ ‎ ‎【巩固】如图，在中，有长方形，、在上，、分别在、上，是 边的高，交于，，厘米，厘米，求长方形的长和宽．‎ 【例 1】 图中是边长为的正方形，从到正方形顶点、连成一个三角形，已知这个三角形在上截得的长度为，那么三角形的面积是多少？‎ ‎ ‎ 【例 2】 如图，将一个边长为的正方形两边长分别延长和，割出图中的阴影部分，求阴影部分的面积是多少？‎ 【例 1】 图中的大小正方形的边长均为整数(厘米)，它们的面积之和等于52平方厘米，则阴影部分的面积是 ．‎ 【例 2】 如图，是矩形一条对角线的中点，图中已经标出两个三角形的面积为和，那么阴影部分的一块直角三角形的面积是多少？‎ 【例 3】 已知长方形的面积为厘米，是的中点，、是边上的三等分点，求阴影的面积是多少厘米？‎ ‎ ‎ 【例 4】 是平行四边形，面积为72平方厘米，、分别为、的中点，则图中阴影部分的面积为 平方厘米．‎ ‎ ‎ 【例 5】 如图，三角形的面积是8平方厘米，长方形的长是‎6厘米，宽是‎4厘米，是的中点，则三角形 的面积是 平方厘米．‎ ‎ ‎ 【例 1】 如图，长方形中，为的中点，与、分别交于、，垂直于，交于，已知，，求．‎ 【例 2】 右图中正方形的面积为1， 、分别为、的中点，．求阴影部分的面积．‎ ‎ ‎ 【例 3】 梯形的面积为12，，为的中点，的延长线与交于，四边形 的面积是 ．‎ ‎ ‎ 【例 4】 如图，三角形的面积为60平方厘米，、、分别为各边的中点，那么阴影部分的面积是 ‎ 平方厘米．‎ ‎ ‎ 【例 1】 如图,是直角梯形，，那么梯形的面积是多少?‎ ‎ ‎ 【例 2】 边长为厘米和厘米的两个正方形并放在一起，那么图中阴影三角形的面积是多少平方厘米？‎ ‎　　　　　　　‎ 【例 3】 如右图，长方形中，，，求的长．‎ 【例 4】 如图，已知正方形的边长为，是边的中点，是边上的点，且，与相交于点 ‎，求 【例 1】 如图所示，已知平行四边形的面积是1，、是、的中点， 交于，求的面积． ‎ ‎ ‎ 【例 2】 正方形的面积是120平方厘米，是的中点，是的中点，四边形的面积是 ‎ 平方厘米． ‎ ‎ ‎ 【例 3】 如图，已知,点分别在上，且，则是多少？ ‎ ‎ ‎ 【例 1】 如图，长方形中，、分别为、边上的点，，，求．‎ ‎ ‎ 【例 2】 如下图，、、、均为各边的三等分点，线段和把三角形分成四部分，如果四边形的面积是24平方厘米，求三角形的面积．‎ ‎ ‎ 【例 3】 如图，为正方形，且，请问四边形的面积为多少？‎ ‎ ‎ 【例 1】 如图12-6所示，在三角形ABC中，DC=3BD，DE=EA．若三角形ABC的面积是1．则阴影部分的面积是多少?‎ 【例 2】 一个等腰直角三角形和一个正方形如图摆放，①、②、③这三块的面积比依次为．那么，④、⑤这两块的面积比是______．‎ 【例 3】 下图中，四边形ABCD都是边长为1的正方形，E、F、G、H分别是AB、BC、CD、DA的重点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数 ‎，那么，m＋n的值等于__________。‎ ‎（A）5 （B）7 （C）8 （D）12‎ 【例 1】 如图所示，三角形AEF，三角形BDF,三角形BCD，都是正三角形，其中AE:BD=1:3,三角形AEF的面积是1.求阴影部分的面积。‎ 【例 2】 如图，正方形ABCD中，E、F、G、H分别为各边的中点，J为GD的中点，EJ交CD于I。已知正方形ABCD边长为10cm，则图中阴影部分的面积是__ ___ cm2.‎