六年级数学下册第6章《整理与复习》数学思考（探究模式的策略（例1）课件（新版）新人教版 16页

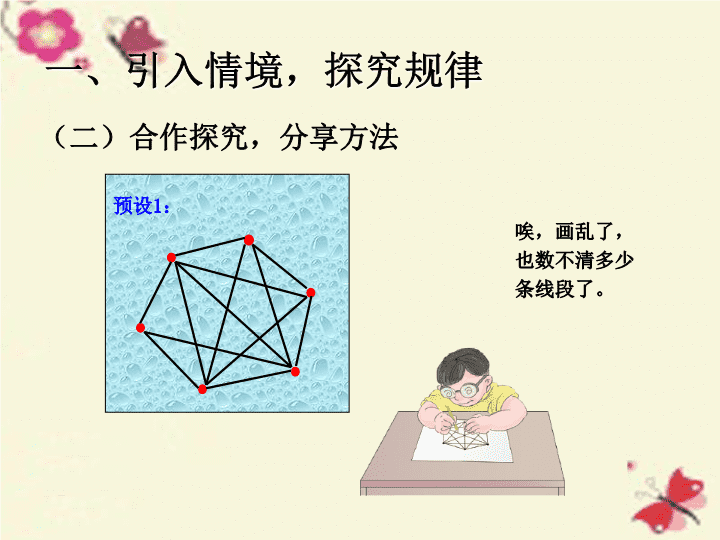
4. 数学思考 探究模式的策略 例 1 整理和复习 一、引入情境，探究规律 （一）出示信息，明确问题 问题：你想怎样解决这个问题？动手试一试吧。 最多有 2 个点在同一条直线上，那么 6 个点可以连多少条线段？ 8 个点呢？ （二）合作探究，分享方法 预设 1 ： 一、引入情境，探究规律 唉，画乱了，也数不清多少条线段了。 不重复，不遗漏。 问题：想一想，按顺序画有什么好处？ 预设 2 ： 5 ＋ 4 ＋ 3 ＋ 2 ＋ 1 ＝ 15 （条） （二）合作探究，分享方法 一、引入情境，探究规律 别着急。 我来帮你！ （二）合作探究，分享方法 一、引入情境，探究规律 幸亏只有 6 个点，要是有 600 个点就惨了！ 对呀，我们找找规律吧！从最少的 2 个点开始。 点数 增加条数 总条数 2 1 3 2 1 ＋ 2＝3 （条） 4 3 1 ＋ 2 ＋ 3＝ 6 （条） 5 4 1＋2＋3＋ 4 ＝ 10 （条） 6 5 1＋2＋3＋ 4 ＋ 5 ＝ 15 （条） 问题：观察“点数”和“增加条数”，你发现了什么规律？ （二）合作探究，分享方法 一、引入情境，探究规律 1 ＋ 2 ＋ 3 ＋ 4 ＋ 5 ＋ 6 ＋ 7 问题： 1. 按照规律， 8 个点能连几条线段？ 2. 为什么有 8 个点，列式却依次加到 7 呢？ （二）合作探究，分享方法 一、引入情境，探究规律 3. 想一想，能用简单方法计算吗？ ＝ （ 1 ＋ 7 ） ＋ （ 2 ＋ 6 ） ＋ （ 3 ＋ 5 ） ＋ 4 ＝ 28 （条） —— 8 个点 ＝ 8 × 3 ＋ 4 二、应用规律，解决问题 ＝ （ 1 ＋ 11 ） ＋ （ 2 ＋ 10 ） ＋ （ 3 ＋ 9 ） ＋ （ 4 ＋ 8 ） ＋ （ 5 ＋ 7 ） ＋ 6 问题：按照简单的方法计算，你发现了什么？ 1 ＋ 2 ＋ 3 ＋ 4 ＋ 5 ＋ 6 ＋ 7 ＋ 8 ＋ 9 ＋ 10 ＋ 11 ＝ 66 （条） —— 12 个点 ＝ 12 × 5 ＋ 6 1. 根据规律，你知道 12 个点、 20 个点能连多少条线段吗？ 二、应用规律，解决问题 1. 根据规律，你知道 12 个点、 20 个点能连多少条线段吗？ 1 ＋ 2 ＋ 3 ＋ 4 ＋ 5 ＋ 6 ＋ 7 ＋ 8 ＋ 9 ＋ 10 ＋ 11 ＋ 12 ＋ 13 ＋ 14 ＋ 15 ＋ 16 ＋ 17 ＋ 18 ＋ 19 ＝ （ 1 ＋ 19 ） ＋ （ 2 ＋ 18 ） ＋ （ 3 ＋ 17 ） ＋ …… ＋ （ 8 ＋ 12 ） ＋ （ 9 ＋ 11 ） ＋ 10 ＝ 20 × 9 ＋ 10 ＝ 190 （条） —— 20 个点 观察下图，想一想。 （ 1 ）第 7 幅图有多少个棋子？第 15 幅图呢？ 问题： 1 . 你想怎样解决这个问题？ 2. 从最简单的数据开始，数一数每幅图各有多少个棋子？ 三、巩固练习，提升认识 3. 在数的过程中，你发现了什么？ 每行的棋子数 × 行数 ＝ 棋子总数 1 × 1 2 × 2 3 × 3 4 × 4 1 4 9 16 问题： 1 . 第 7 幅图每行有几个棋子？有几行？共有几个棋子？ 3. 第 15 幅图共有几个棋子？ 三、巩固练习，提升认识 7 × 7 ＝ 49 （个） 15 × 15 ＝ 225 （个） 观察下图，想一想。 （ 1 ）第 7 幅图有多少个棋子？第 15 幅图呢？ 2. 每边的棋子数与图形的序号有什么关系？ 观察下图，想一想。 （ 2 ）第 n 幅图有多少个棋子？ 问题：第 n 幅图每边有多少个棋子？一共有多少个棋子？ 三、巩固练习，提升认识 每行的棋子数 × 行数 ＝ 棋子总数 n × n ＝ 棋子总数 n 2 ＝ 棋子总数 问题：遇到复杂的问题，你可以怎样思考？ 三、巩固练习，提升认识 3. 有序思考 2. 画图、枚举 1. 化繁为简 4. 探究规律 四、布置作业 作业：第 103 页练习二十二， 第 1 、 2 、 3 、 4 题。