六年级数学上册第六单元百分数（一）解决问题教学课件（完美版） 56页

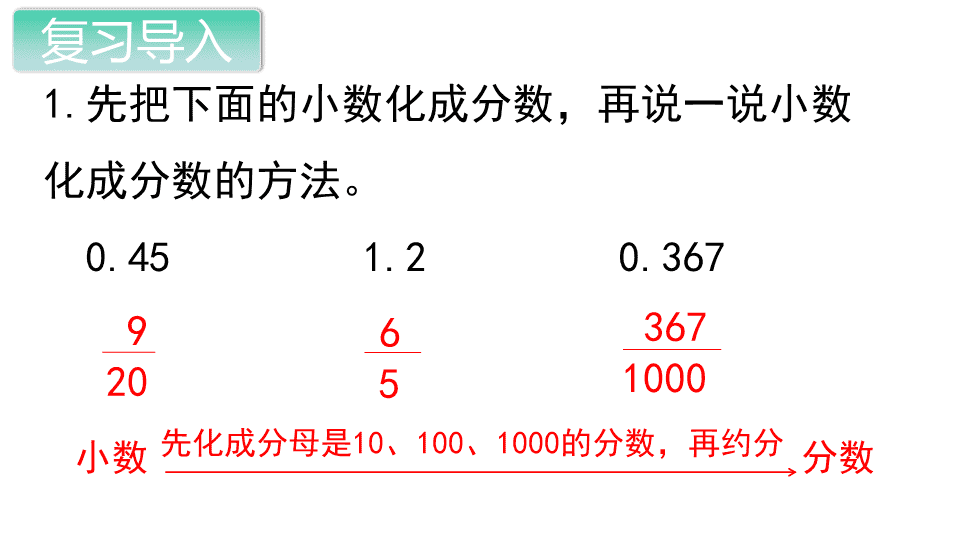
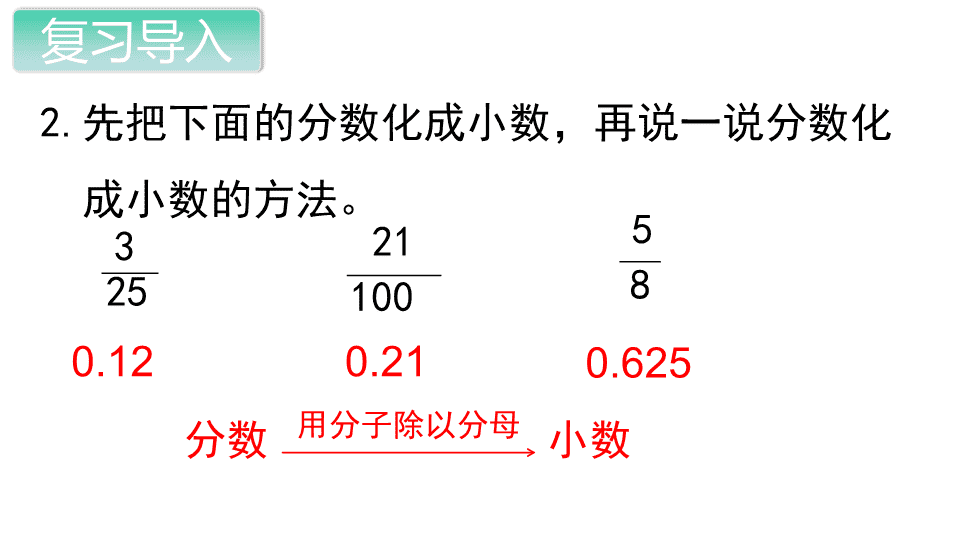
解决问题 1.先把下面的小数化成分数，再说一说小数 化成分数的方法。 0.45 1.2 0.367 9 20 6 5 367 1000 复习导入 先化成分母是10、100、1000的分数，再约分小数 分数 2.先把下面的分数化成小数，再说一说分数化 成小数的方法。 3 25 5 8 21 100 0.12 0.21 0.625 复习导入 用分子除以分母分数 小数 他们两人的命中率分别是多少?谁的命中率高？ 我5投3中。 我6投4中。 王涛 李强 1 已知条件 王涛5投3中，李强6投4中。 所求问题 两人的命中率分别是多少？谁命中率高？ 新知探究 命中率指的是投中的次数占投篮次数的百分之几。 梳理信息，分析思路 他们两人的命中率分别是多少?谁的命中率高？ 我5投3中。 我6投4中。 王涛 李强 1 新知探究 方法一： 100 603÷5＝0.6＝ ＝60%王涛 1000 6674÷6≈0.667＝ ＝66.7 %李强 除不尽时， 通常保留三 位小数 先把小数改写成分母是100的分数，再化成百分数。 他们两人的命中率分别是多少?谁的命中率高？ 我5投3中。 我6投4中。 王涛 李强 1 新知探究 王涛 100 603÷5＝ ＝60%5 3 ＝ 3×20 5×20 ＝ 6 4李强 4÷6= =…… 把 改写成分母是100的分数，再化成百分数。5 3 方法二： 他们两人的命中率分别是多少?谁的命中率高？ 我5投3中。 我6投4中。 王涛 李强 1 新知探究 100 603÷5＝0.6＝ ＝60%王涛 1000 6674÷6≈0.667＝ ＝66.7 %李强 答：王涛和李强的命中率分别是60%和66.7%。 李强的命中率高些。 规范解答 在实际生活中，像上面这样的常用的百分率还有许多。如 学生的出勤率、绿豆的发芽率、产品的合格率、小麦的出粉率、 树木的成活率等。 出勤率= ×100%出勤的学生人数 学生总人数 发芽率= ×100% （ ） （ ） 发芽种子数 实验种子数 你还能说出一些 百分率的例子吗？ 新知探究 百分率是指部分量占总量的百分之几， 计算方法是用部分量除以总量再化成百分数。 求百分率 课堂小结 把小数和分数化成百分数 把小数化成百分数，只需要把小数点向右 移动两位，同时在后面添上百分号；把分数化 成百分数，通常先把分数化成小数，除不尽时， 通常保留三位小数，再化成百分数。 课堂小结 1、（教材P85T2）六年级有学生160人，已达到 国家体育锻炼标准的有120人。六年级学生 的体育达标率是多少？ 120÷160X100℅=75% 答：六年级学生的体育达标率是75%。 巩固练习 2、将10千克黄豆榨得2.5千克油，出油率是 多少？ 巩固练习 2.5÷10×100%=25% 答： 出油率是 25% 。 3、六（一）班全班50人,参加劳动有42人,则该 班的参与率为多少？ 42÷50×100%=84% 答：该班的参与率为 84% 。 巩固练习 4、欣欣服装店的某件上衣进价200元，店主以 280元的价格卖出。这件上衣的利润率是多少？ （280-200）÷200=40% 答：这件上衣的利润率是40%。 拓展练习 1.把下面各数化成百分数。 0.37 1.45 0.99 6 37% 145% 99% 600% 复习导入 复习导入 2.把分数化成百分数。 3.什么样的分数能化成有限小数？什么样的分 数不能化成有限小数？ 11 8 2 5 1 4 2 3 9 25 25% 40% 137.5% 36% 67% 复习导入 春蕾小学的一项调查表明，有牙病的学生人数占全 校人数的20%。春蕾小学共有750名学生，有牙病的学 生有多少人？ 求一个数的百分之几和求一个 数的几分之几，意义一样吗？ 2 新知探究 1.梳理信息，分析思路 已知条件 有牙病学生人数占全校人数的20%，小学 共有750名学生。 所求问题 有牙病的学生有多少人？ 2 新知探究 方法一： 750×20%=750× =750×0.2 =150（人） 20 100 我把百分数改写成分母是100 的分数，再直接写成小数。 把百分数化成小数，只要小 数点向左移动…… 春蕾小学的一项调查表明，有牙病的学生人数占全 校人数的20%。春蕾小学共有750名学生，有牙病的学 生有多少人？ 春蕾小学的一项调查表明，有牙病的学生人数 占全校人数的20%。春蕾小学共有750名学生，有牙 病的学生有多少人？ 2 新知探究 方法二： 750×20%=750× =750× =150（人） 20 100 1 5 我把百分数改写成分母是100 的分数，直接用分数乘法计算。 百分数本来就是一种特 殊的分数…… 2 新知探究 答：有牙病的学生有150人。 750×20%=750× =750× =150（人） 20 100 1 5 方法二：方法一： 750×20%=750× =750×0.2 =150（人） 20 100 春蕾小学的一项调查表明，有牙病的学生人数占全 校人数的20%。春蕾小学共有750名学生，有牙病的学 生有多少人？ 求一个数的百分之几是多少 求一个数的百分之几与求一个数的几分 之几的意义相同，数量关系是这个数乘百分 之几。计算时可以把百分数化成小数或分数， 再计算。 课堂小结 把百分数改写成小数或分数 把百分数改成小数，只要把百分号去掉， 同时把小数点向左移动两位；把百分数改成 分数，可以看做分母是100、1000...的分数， 再约分成为最简分数。 课堂小结 1.把下面的小数和分数改成百分数，百分数改 成小数和分数。 0.97=97% 0.08 =8% 8 1 =12.5% 6 1 ≈0.167=16.7% 0.5% =0.005= 1 200 25% =0.25= 4 1 巩固练习 2.（教材P85T3）六年级一班有45名学生，上学 期期末跳远测验有80%的人及格。及格的同学 有多少人？ 45×80%=36（人） 答：及格的同学有36人。 巩固练习 3.100个零件，3%是不合格的，不合格的有多 少个？取出25个合格的零件后，不合格的目 前占了百分之几？ 不合格零件：100×3% = 3（个） 取出后： 3 ÷ (100-25)×100% = 4% 答：不合格的目前占了4%。 拓展训练 1.说说下面每个百分数的具体含义。 （1）某种花生的出油率是35%。 （2）实际用电量占计划用电量的80%。 （3）李庄今年荔枝产量是去年的120%。 复习导入 这样的数量关系和分数乘除 法问题的数量关系类似。这 里是求比原计划多造林的面 积是计划的百分之几？ 3 1.梳理信息，分析思路 已知条件 原计划造林12公顷，实际造林14公顷。实际造 林比原计划增加了16.7%。 所求问题 比原计划多造林的面积是计划的百分之几？ 新知探究 3 新知探究 （14-12）÷12 =2÷12 ≈0.167 =16.7%方法一：原计划： 12公顷实际： 14公顷 比原计划 多造的 2、解题探究 3 新知探究 方法二：原计划： 12公顷实际： 14公顷 比原计划 多造的 14÷12≈1.167＝116.7% 116.7%－100%＝16.7% 也可以先求 实际造林是 原计划的百 分之几？ 2、解题探究 3 新知探究 （14-12）÷12=2÷12≈0.167=16.7%方法一： 方法二：14÷12≈1.167＝116.7% 116.7%－100%＝16.7% 答：实际造林是原计划的16.7%。 3.规范解答 在实际生活中，人们常用“增加百分之几”“减 少百分之几”“节约百分之几”……来表示增加、减 少的幅度。 你知道上面这些话的含义吗？ 举例说一说。 新知探究 求一个数比另一个数多（或少）百分之几 求一个数比另一个数多（或少）百分之几，可以先 求多（或少）的部分，再求多（或少）的部分是另一 个数的百分之几；也可以先求一个数是另外一个数的 百分之几，再求比另外一个数多（或少）百分之几。 课堂小结 1.甲数是25，乙数是20，甲数比乙数多（ ）%， 乙数比甲数少（ ）%。 25 20 2. 5米比4米多（ ）%，4米比5米少（ ）%。25 20 3.一种电风扇原售价每台200元，现售价160元，降低 了（ ）%。20 巩固练习 4.（教材P89页）小飞家原来每月用水约10t， 更换了节水龙头后每月用水约9t，每月用水 比原来节约了百分之几？ （10-9）÷10=10% 答：每月用水比原来节约了10%。 巩固练习 根据下列一组信息，能提出哪些数学问题？ （1）学校图书室原有图书1400册。 （2）今年图书册数增加了 。3 25 复习导入 学校图书室原有图书1400册，今年图书册数增加 了12%。现在图书室有多少册图书？ 4 已知条件 原有图书1400册，今年图书册数增 加了12%。 所求问题 现在图书室有多少册图书？ 梳理信息，分析思路 创设情境 学校图书室原有图书1400册，今年图书册数增加 了12%。现在图书室有多少册图书？ 4 解法探究 创设情境 方法一：1400×12%=168（册） 1400+168=1568（册） 把“1400册”看作单 位“1”。 先求出增加 的图书数量 学校图书室原有图书1400册，今年图书册数增加 了12%。现在图书室有多少册图书？ 4 解法探究 创设情境 今年图书册数是去年的 百分之（1+12%） 方法二： 1400×（1+12%） =1400×112% = （册）1568 学校图书室原有图书1400册，今年图书册数增加 了12%。现在图书室有多少册图书？ 4 规范解答 创设情境 答：现在图书室有1568册图书。 方法一：1400×12%=168（册） 1400+168=1568（册） 1400×（1+12%） =1400×112% = （册）1568 方法二： 求比一个数多（或少）百分之几的数是多少 求比一个数多（或少）百分之几的数是多少与 求比一个数多（或少)几分之几的思路相同；方法一 是先求多（或少）的数，方法二是先求要求的数是 这个数的百分之几。 课堂小结 　 1.50千克增加它的20%是（ ）千克，50千克 减少它的20%是（ ）千克。 60 40 1 2.某班有50位学生，一次数学测试的合格率 是98%，那么不合格的人数为（ ）。 巩固练习 3.（教材P91页）龙泉镇去年有小学生2800人， 今年比去年减少了0.5%。今年有小学生多少人？ 2800×（1-0.5%）=2786（人） 答：今年有小学生2786人。 巩固练习 解法一： 80000-80000×0.5% =80000-400 =79600（人） 解法二： 80000×（1- 0.5% ） =80000×99.5% =79600（人） 4.一个县去年有在校小学生80000人，今年比去年 减少了0.5%。这个县今年有在校小学生多少人？ 答：这个县今年有在校小学生79600人。 拓展练习 说一说下面各题中表示单位“1”的量。 （1）连环画的本数是故事书本数的37.5%。 （2）美术小组的人数相当于科技小组人数的60% 。 （3）冰箱价格的 是洗衣机的价格。2 1 （4）苹果树的棵数是梨树棵数的 ，桃树棵数是 苹果树棵数的 。 4 3 2 3 复习导入 某种商品4月的价格比3月降了20%，5月的价格比4月 又涨了20%。5月的价格和3月比是涨了还是降了？变 化幅度是多少？ 5 1.梳理信息，分析思路 已知条件 4月的价格比3月降了20%，5月的价格比4 月又涨了20%。 所求问题 5月的价格和3月比是涨了还是降了？变 化幅度是多少？ 创设情境 某种商品4月的价格比3月降了20%，5月的价格比4月 又涨了20%。5月的价格和3月比是涨了还是降了？变 化幅度是多少？ 5 现在我们只知道每两个月之间价格的 变化幅度，但商品原来的价格却未知， 想一想可以怎么办呢？ 你会解答吗？ 新知探究 某种商品4月的价格比3月降了20%，5月的价格比4月 又涨了20%。5月的价格和3月比是涨了还是降了？变 化幅度是多少？ 5 2.解法探究（1）4月份价格： 100 ×（1－20%）＝100 ×80%＝80（元） （2）5月份价格： 80 ×（1＋20%）＝80 ×120%＝96（元） 方法一： 可以假设此商品3月的价格是100元。 新知探究 某种商品4月的价格比3月降了20%，5月的价格比4月 又涨了20%。5月的价格和3月比是涨了还是降了？变 化幅度是多少？ 5 方法一： （3）5月份和3月份价格比较： 96元＜100元 （4）变化幅度： （100－96）÷100＝4 ÷100＝4% 答：5月的价格和3月比降了，变化幅度是降低了4%。 2.解法探究 可以假设此商品3月的价格是100元。 新知探究 某种商品4月的价格比3月降了20%，5月的价格比4月 又涨了20%。5月的价格和3月比是涨了还是降了？变 化幅度是多少？ 5 方法二： 2.解法探究 1×（1－20%）×（1＋20%）＝0.96 （1－0.96）÷1＝0.04＝4% 答：5月的价格和3月比降了，变化幅度是降低了4%。 也可以直接假设此商品3月的价格是1。 新知探究 方法一：100 ×（1－20%）＝100 ×80%＝80（元） 80 ×（1＋20%）＝80 ×120%＝96（元） 96元＜100元 （100－96）÷100＝4 ÷100＝4% 3.规范解答 方法二： 1×（1－20%）×（1＋20%）＝0.96 （1－0.96）÷1＝0.04＝4% 答：5月的价格和3月比降了，变化幅度是降低了4%。 新知探究 如果此商品3月的价格是 a元呢？结论是否一致？ 5 a×（1－20%）×（1＋20%）＝0.96a （a－0.96a）÷a＝0.04＝4% 答：5月的价格和3月比降了，变化幅 度是降低了4%。 某种商品4月的价格比3月降了20%，5月的价格比4月 又涨了20%。5月的价格和3月比是涨了还是降了？变 化幅度是多少？ 新知探究 5 某种商品4月的价格比3月降了20%，5月的价格比4月 又涨了20%。5月的价格和3月比是涨了还是降了？变 化幅度是多少？ 虽然降价和涨价幅度都 是20%，但降价和涨价 的具体钱数却不同。 同学们想一想，为什么降价和涨价的幅度都是20%， 但降价和涨价的具体钱数却不同呢？ 因为单位“1”不同。 新知探究 课堂小结 1.在解答已知一个数量的两次增减变化幅度，即先 减少百分之几，再增加百分之几，求最后变化幅度 的问题时，可以先用设数法，把单位“1”设为一个 具体数或1来解答。 课堂小结 2.按1解答时，最后的变化幅度为1与“1×（1-减少 幅度）×（1+增加幅度）”的差除以1所得的百分数。 3.在前后增、减幅度相同时，两次增减的具体数量不 同，减少的具体数量要多于增加的具体数量。 1.为了缓解交通拥挤的状况，某市正在进行道 路拓宽。团结路的路宽由原来的12m增加到25m， 拓宽了百分之几？ （25-12）÷12≈108.3% 答：拓宽了108.3%。 巩固练习 2.某电视机厂计划某种型号的电视机比去年增产 50%，实际又比计划的产量多生产了10%。此型号 的电视机今年的实际产量是去年的百分之多少？ 假设去年的产量为1。 1×（1+50%）×（1+10%）÷1=165% 答：此型号的电视机今年的实际产量是去年的165%。 巩固练习