小升初数学模拟试卷及解析（25）人教新课标 14页

小升初数学模拟试卷及解析（25）|人教新课标（2014秋）‎ ‎　‎ 一、填空，根据理解和记忆将（）的内容正确填写好．‎ ‎1．圆的周长和直径的比值叫　　　　　　，用字母　　　　　　表示．‎ ‎　‎ ‎2．（3分）在同一个圆里，所有的直径都　　　　　　，所有的半径都　　　　　　，直径的长度是半径的　　　　　　倍．‎ ‎　‎ ‎3．圆的直径扩大3倍，它的周长扩大　　　　　　倍，面积扩大　　　　　　倍．‎ ‎　‎ ‎4．（2分）全国大约13.3亿人，如果每人每天节约1分钱，那么全国每天可以节约　　　　　　元；如果建一所希望小学约需130万元，那么全国每天节约的钱大约可以建　　　　　　所希望小学．‎ ‎　‎ ‎5．（2分）一只书包大约重3.5　　　　　　，我的平均步长约是　　　　　　．‎ ‎　‎ ‎6．（2分）工人叔叔把电线杆上的线架和自行车架子做成三角形，这是应用了三角三具有　　　　　　的特征，而推拉或防盗门则是由许多小平边四边形组成的，这是应用平行四边形　　　　　　的特性．‎ ‎　‎ ‎7．（3分）大圆的半径是小圆的6倍，小圆周长是大圆的　　　　　　，大圆面积是小圆面积的　　　　　　．‎ ‎　‎ ‎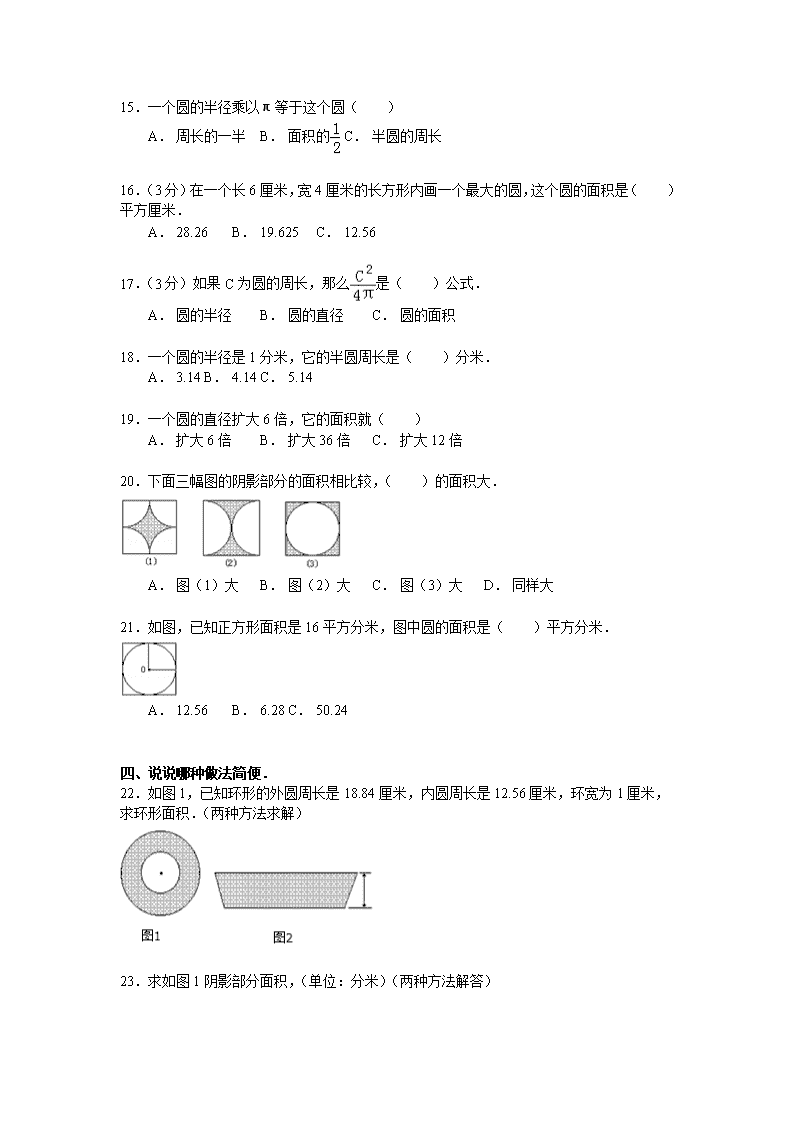8．一个半圆形的花坛周长是‎30.84米，这个半圆形花坛的面积是　　　　　　．‎ ‎　‎ ‎　‎ 二、判断，正确的画“√”，错误的画“×”．‎ ‎9．（3分）一个圆的周长是它半径的2π倍．　　　　　　（判断对错）‎ ‎　‎ ‎10．圆的直径就是这个圆的对称轴．　　　　　　．（判断对错）‎ ‎　‎ ‎11．半圆的周长是和它相等半径的圆周长的一半．　　　　　　．（判断对错）‎ ‎　‎ ‎12．通过圆心的线段叫直径．　　　　　　．（判断对错）‎ ‎　‎ ‎13．半径是2厘米的圆，它的周长和面积相等．　　　　　　．（判断对错）‎ ‎　‎ ‎14．一个圆的直径等于一个正方形的边长，那么正方形的面积小于圆的面积．　　　　　　．（判断对错）‎ ‎　[来源:Z§xx§k.Com]‎ ‎　‎ 三、选择，将正确答案的序号填在（）里．‎ ‎15．一个圆的半径乘以π等于这个圆（　　）‎ ‎　 A． 周长的一半 B． 面积的 C． 半圆的周长 ‎　‎ ‎16．（3分）在一个长6厘米，宽4厘米的长方形内画一个最大的圆，这个圆的面积是（　　）平方厘米．‎ ‎　 A． 28.26 B． ‎19.625 ‎C． 12.56‎ ‎　‎ ‎17．（3分）如果C为圆的周长，那么是（　　）公式．‎ ‎　 A． 圆的半径 B． 圆的直径 C． 圆的面积 ‎　‎ ‎18．一个圆的半径是1分米，它的半圆周长是（　　）分米．‎ ‎　 A． 3.14 B． ‎4.14 ‎C． 5.14‎ ‎　‎ ‎19．一个圆的直径扩大6倍，它的面积就（　　）‎ ‎　 A． 扩大6倍 B． 扩大36倍 C． 扩大12倍 ‎　‎ ‎20．下面三幅图的阴影部分的面积相比较，（　　）的面积大．‎ ‎　 A． 图（1）大 B． 图（2）大 C． 图（3）大 D． 同样大 ‎　‎ ‎21．如图，已知正方形面积是16平方分米，图中圆的面积是（　　）平方分米．‎ ‎　 A． 12.56 B． ‎6.28 ‎C． 50.24‎ ‎　‎ ‎　‎ 四、说说哪种做法简便．‎ ‎22．如图1，已知环形的外圆周长是18.84厘米，内圆周长是12.56厘米，环宽为1厘米，求环形面积．（两种方法求解）‎ ‎　‎ ‎23．求如图1阴影部分面积，（单位：分米）（两种方法解答）[来源:学#科#网]‎ ‎　‎ ‎　‎ 五、解答下面各题 ‎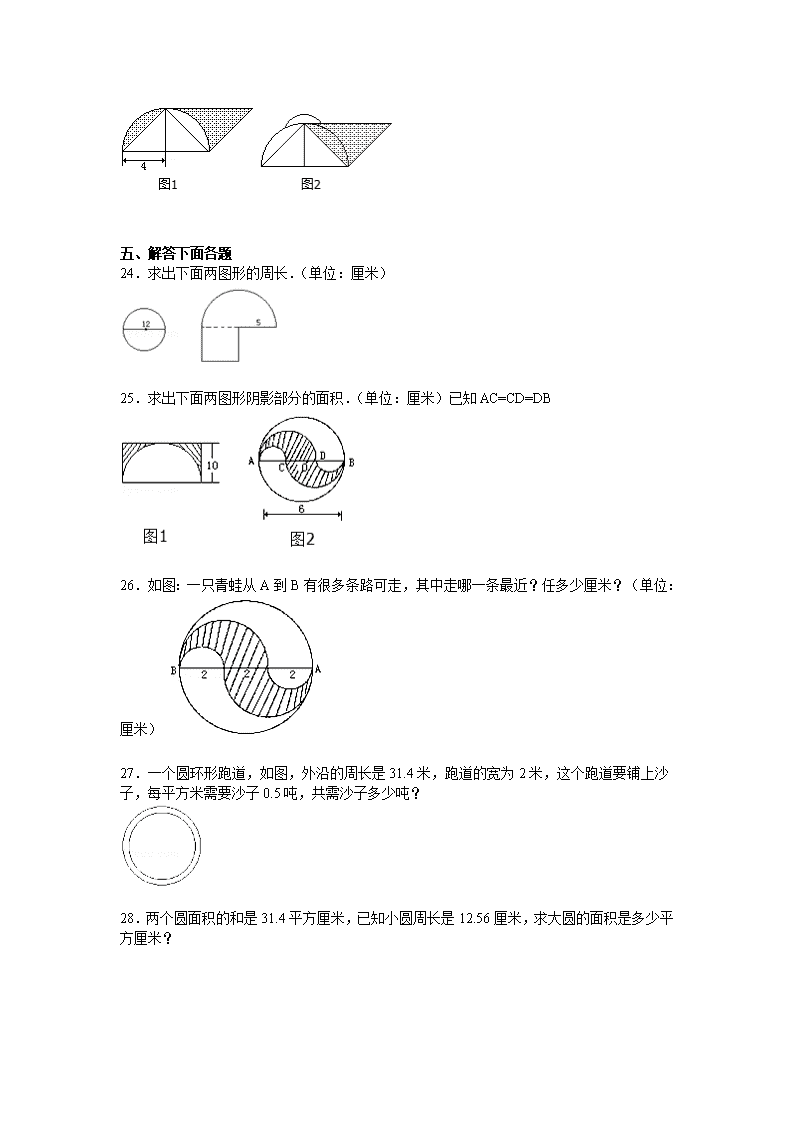24．求出下面两图形的周长．（单位：厘米）‎ ‎　‎ ‎25．求出下面两图形阴影部分的面积．（单位：厘米）已知AC=CD=DB ‎　‎ ‎26．如图：一只青蛙从A到B有很多条路可走，其中走哪一条最近？任多少厘米？（单位：厘米） ‎ ‎　‎ ‎27．一个圆环形跑道，如图，外沿的周长是‎31.4米，跑道的宽为‎2米，这个跑道要铺上沙子，每平方米需要沙子0.5吨，共需沙子多少吨？‎ ‎　‎ ‎28．两个圆面积的和是31.4平方厘米，已知小圆周长是12.56厘米，求大圆的面积是多少平方厘米？‎ ‎　‎ ‎　‎ 参考答案与试题解析 ‎　‎ 一、填空，根据理解和记忆将（）的内容正确填写好．‎ ‎1．圆的周长和直径的比值叫　圆周率　，用字母　π　表示．‎ 考点： 圆的认识与圆周率． ‎ 分析： 根据圆周率的含义：圆的周长和它直径的比值，叫做圆周率；圆周率用字母“π”表示，圆周率π是一个无限不循环小数；进而解答即可．‎ 解答： 解：根据圆周率的含义可知：圆的周长和它直径的比值叫圆周率，用字母“π”表示；‎ 故答案为：圆周率，π．‎ 点评： 解答此题应根据圆周率的含义进行解答．‎ ‎　‎ ‎2．（3分）在同一个圆里，所有的直径都　长度相等　，所有的半径都　长度相等　，直径的长度是半径的　2　倍．‎ 考点： 圆的认识与圆周率． ‎ 分析： 依据圆的认识，及在同一个圆中半径与直径的关系即可作答．‎ 解答： 解：在同一个圆里，所有的直径都长度相等，所有的半径都长度相等，直径的长度是半径的2倍．‎ 故答案为：长度相等，长度相等，2．‎ 点评： 此题主要考查在同一个圆中半径与直径的关系．‎ ‎　‎ ‎3．圆的直径扩大3倍，它的周长扩大　3　倍，面积扩大　9　倍．‎ 考点： 圆、圆环的周长；积的变化规律；圆、圆环的面积． ‎ 专题： 平面图形的认识与计算．‎ 分析： 一个圆的直径扩大n倍，周长就扩大n倍，面积就扩大n2倍；据此解答．‎ 解答： 解：一个圆的直径扩大3倍，周长就扩大3倍，面积就扩大32=9倍．‎ 故答案为：3，9．‎ 点评： 考查了圆的周长公式和圆的面积公式：圆的周长C=πd，圆的面积S=πr2．‎ ‎　‎ ‎4．（2分）全国大约13.3亿人，如果每人每天节约1分钱，那么全国每天可以节约　13300000　元；如果建一所希望小学约需130万元，那么全国每天节约的钱大约可以建　10　所希望小学．‎ 考点： 整数的读法和写法；整数的改写和近似数． ‎ 专题： 整数的认识．‎ 分析： 就是求13.3亿个1分是多少元，把13.3亿化成1330000000，乘1再除以100就是每天节约的元数；把130万元化成1300000元，用这个数去除每天节约的钱数就是可以建希望小学的数量．‎ 解答： 解：13.3亿=1330000000 ‎ ‎1330000000×1÷100=13300000（元）‎ ‎130万元=1300000元 ‎13300000÷1300000≈10（所）．‎ 故答案为：13300000，10．‎ 点评： 此题主查考查整数的改写、人民币的单位换算、整数乘除法的应用、求近似数等．‎ ‎　‎ ‎5．（2分）一只书包大约重3.5　千克　，我的平均步长约是　‎0.5米　．‎ 考点： 根据情景选择合适的计量单位． ‎ 专题： 长度、面积、体积单位；质量、时间、人民币单位．‎ 分析： 根据生活经验、对长度单位、质量单位、和数据大小的认识，可知计量一只书包大约重3.5 千克，我的平均步长约是 ‎0.5米；据此解答即可．‎ 解答： 解：一只书包大约重3.5 千克，我的平均步长约是 ‎‎0.5米 故答案为：千克，‎0.5米．‎ 点评： 本题考查了选择合适的计量单位，计量一些物体要根据生活经验、对长度单位、质量单位、面积单位、体积单位、时间单位和数据大小的认识选择合适的单位．‎ ‎　‎ ‎6．（2分）工人叔叔把电线杆上的线架和自行车架子做成三角形，这是应用了三角三具有　稳定性　的特征，而推拉或防盗门则是由许多小平边四边形组成的，这是应用平行四边形　不稳定性　的特性．‎ 考点： 三角形的特性；平行四边形的特征及性质． ‎ 分析： 直接利用三角形的特性以及四边形的特性解答问题即可．‎ 解答： 解：三角形的特性：三角形具有稳定性；‎ 四边形的特性：四边形具有不稳定性；‎ 故答案为：稳定性，不稳定性．‎ 点评： 此题主要利用三角形的稳定性与四边形的不稳定性解决现实生活中的实际问题．‎ ‎　‎ ‎　‎ ‎7．（3分）大圆的半径是小圆的6倍，小圆周长是大圆的　　，大圆面积是小圆面积的　36倍　．‎ 考点： 圆、圆环的周长；圆、圆环的面积． ‎ 专题： 平面图形的认识与计算．‎ 分析： 设小圆的半径为r，则大圆的半径为6r，分别代入圆的周长和面积公式，表示出各自的周长和面积，即可求解．‎ 解答： 解：设小圆的半径为r，则大圆的半径为6r，‎ 小圆的周长=2πr，‎ 大圆的周长=2π×6r=12πr，‎ ‎12πr÷2πr=6倍；‎ 小圆的面积=πr2，‎ 大圆的面积=π（6r）2=36πr2，‎ ‎36πr2÷πr2=36倍．‎ 故答案为：，36倍．‎ 点评： 此题主要结合积的变化规律考查圆的周长和面积的计算方法的灵活应用．‎ ‎　‎ ‎8．一个半圆形的花坛周长是‎30.84米，这个半圆形花坛的面积是　56.52平方米　．‎ 考点： 圆、圆环的周长；圆、圆环的面积． ‎ 专题： 平面图形的认识与计算．‎ 分析： 根据半圆的周长=圆周长的一半+直径，列方程求出直径，然后再利用圆的面积公式S=πr2求出整圆的面积，进而求出半圆的面积．‎ 解答： 解：设圆形花坛的直径是d米，‎ ‎3.14×d÷2+d=30.84，‎ ‎ 2.57d=30.84，‎ ‎ d=12；‎ 面积为：3.14×（12÷2）2÷2；‎ ‎=3.14×36÷2，‎ ‎=56.52（平方米）；‎ 答：这个半圆形花坛的面积是56.52平方米；‎ 故答案为：56.52平方米．‎ 点评： 本题根据“半圆的周长=圆周长的一半+直径”求出直径是解答关键；本题用到的知识点还有圆的周长公式：C=πd；圆的面积公式：S=πr2．‎ ‎　‎ 二、判断，正确的画“√”，错误的画“×”．‎ ‎9．（3分）一个圆的周长是它半径的2π倍．　√　（判断对错）‎ 考点： 圆、圆环的周长． ‎ 专题： 平面图形的认识与计算．‎ 分析： 根据“圆的周长=2πr”可知：圆的周长÷r=2π；可知：圆的周长是它半径的2π倍；由此判断即可．‎ 解答： 解：圆的周长是它半径的2π倍；‎ 故答案为：√．‎ 点评： 解答此题应根据圆的半径、圆周率和圆的周长三者之间的关系．‎ ‎　‎ ‎10．圆的直径就是这个圆的对称轴．　错误　．（判断对错）‎ 考点： 轴对称． ‎ 分析： 根据轴对称图形的意义，一个图形沿一条直线将图形对折，两边的图形能够完全重合这样的图形叫做轴对称图形．由此解答．‎ 解答： 解：对称轴是直线，而直径是线段，所以应该说圆的对称轴是直径所在直线．‎ 故答案为：错误．‎ 点评： 此题解答关键是明确线段有两个端点，直线没有端点可以项两方无限延长；圆的直径是线段，而对称轴是直线．据此解决问题．‎ ‎　‎ ‎11．半圆的周长是和它相等半径的圆周长的一半．　×　．（判断对错）‎ 考点： 圆、圆环的周长． ‎ 分析： 首先要区分“半圆的周长”和“圆周长的一半”的区别，半圆的周长是在圆周长一半的基础上再加上直径的长度，这两者之间是有本质的区别的，由此可以进行判断．‎ 解答： 解：由题意知，“半圆的周长”和“圆周长的一半”是不一样的，‎ 半圆的周长是在圆周长一半的基础上再加上直径的长度，圆周长的一半是一段弧，‎ 二者还可以更清晰的表示为下图：‎ 所以上面的说法是错误的，‎ 故答案为：×．‎ 点评： 此题考查了“半圆的周长”和“圆周长的一半”的区别．‎ ‎　‎ ‎12．通过圆心的线段叫直径．　错误　．（判断对错）‎ 考点： 圆的认识与圆周率． ‎ 分析： 通过圆心且两端都在圆上的线段叫直径，题目中没说两端在圆上，所以根据此点可以进行判断．‎ 解答： 解：由直径的定义知：直径要过圆心，且两端都在圆上，所以题目中的说法不正确；‎ 故答案为：错误．‎ 点评： 此题考查了直径的定义．‎ ‎　‎ ‎13．半径是2厘米的圆，它的周长和面积相等．　×　．（判断对错）‎ 考点： 圆、圆环的周长；圆、圆环的面积． ‎ 专题： 压轴题．‎ 分析： 圆的周长是长度单位厘米，圆的面积是面积单位平方厘米，两者之间不能互换，因此无法比较大小．‎ 解答： 解：圆的周长是长度单位厘米，圆的面积是面积单位平方厘米，两者之间不能互换，因此无法比较大小．‎ 答：半径是2厘米的圆，它的周长和面积不能进行大小的比较．‎ 故答案为：×．‎ 点评： 此题主要考查的是不能互换的两单位之间也不能进行大小的比较．‎ ‎　‎ ‎14．一个圆的直径等于一个正方形的边长，那么正方形的面积小于圆的面积．　错误　．（判断对错）‎ 考点： 面积及面积的大小比较． ‎ 专题： 压轴题；平面图形的认识与计算．‎ 分析： 我们通过计算出圆与正方形的面积，进行比较后就较容易作出判断，把它们的结果化成同分母的方式进行比较即可．‎ 解答： 解：设圆的直径是x，正方形的边长也是x．‎ 圆的面积：‎ ‎3.14×，‎ ‎=3.14×‎ ‎=，‎ ‎=，‎ 正方形的面积：‎ x×x=；‎ 所以＜，‎ 即，正方形的面积＞圆的面积．‎ 故答案为：错误 点评： 本题是一道复杂的面积比较题，考查了学生圆与正方形的面积公式的运用情况．‎ ‎　‎ 三、选择，将正确答案的序号填在（）里．‎ ‎15．一个圆的半径乘以π等于这个圆（　　）‎ ‎　 A． 周长的一半 B． 面积的 C． 半圆的周长 考点： 圆、圆环的周长． ‎ 专题： 平面图形的认识与计算．‎ 分析： 根据圆的周长=2πr，圆的面积=πr2，半圆的周长=圆的周长的一半+直径，分别用π和r表示出三个选项中数据，即可选择符合题意的选项．‎ 解答： 解：A：周长的一半是：2πr÷2=πr，符合题意；‎ B：面积的一半是：πr2÷2=r2，不符合题意；‎ C：半圆的周长是：2πr÷2+2r=πr+2r，不符合题意，‎ 所以一个圆的半径乘以π等于这个圆的周长的一半，‎ 故选：A．‎ 点评： 此题主要考查圆的周长和面积公式的灵活应用．[来源:学科网ZXXK]‎ ‎　‎ ‎16．（3分）在一个长6厘米，宽4厘米的长方形内画一个最大的圆，这个圆的面积是（　　）平方厘米．‎ ‎　 A． 28.26 B． ‎19.625 ‎C． 12.56‎ 考点： 圆、圆环的面积． ‎ 专题： 平面图形的认识与计算．‎ 分析： 长方形内最大的圆的直径等于长方形的最短边4厘米，据此利用圆的面积公式计算即可．‎ 解答： 解：3.14×（4÷2）2‎ ‎=3.14×4‎ ‎=12.56（平方厘米）．‎ 答：这个圆的面积是12.56平方厘米．‎ 故选：C．‎ 点评： 解答此题的关键是明确长方形内最大的圆的直径，再利用圆的面积公式计算即可解答．‎ ‎　[来源:学科网]‎ ‎17．（3分）如果C为圆的周长，那么是（　　）公式．‎ ‎　 A． 圆的半径 B． 圆的直径 C． 圆的面积 考点： 圆、圆环的面积；圆、圆环的周长． ‎ 专题： 平面图形的认识与计算．‎ 分析： 根据圆的周长公式：C=2πr，可知==πr2，再根据圆的面积公式即可求解．‎ 解答： 解：==πr2．‎ 故是圆的面积公式．‎ 故选：C．‎ 点评： 此题主要考查的是圆的周长公式、面积公式的掌握情况．‎ ‎　‎ ‎18．一个圆的半径是1分米，它的半圆周长是（　　）分米．‎ ‎　 A． 3.14 B． ‎4.14 ‎C． 5.14‎ 考点： 圆、圆环的周长． ‎ 专题： 平面图形的认识与计算．‎ 分析： 半圆的周长=整圆的周长÷2+直径，由此代入数据，即可解答．‎ 解答： 解：3.14×1×2÷2+1×2‎ ‎=3.14+2，‎ ‎=5.14（分米），‎ 答：它的半圆周长是5.14分米；‎ 故选：C．‎ 点评： 此题考查半圆的周长的计算方法，注意半圆的周长等于圆周长的一半加圆的直径．‎ ‎　‎ ‎19．一个圆的直径扩大6倍，它的面积就（　　）‎ ‎　 A． 扩大6倍 B． 扩大36倍 C． 扩大12倍 考点： 圆、圆环的面积；积的变化规律． ‎ 专题： 平面图形的认识与计算．‎ 分析： 因为d=2r，一个圆的直径扩大6倍，则其半径也扩大6倍，圆的面积=πr2，所以圆的面积与半径的平方成正比例关系，据此解答即可．‎ 解答： 解：因为d=2r，一个圆的直径扩大6倍，则其半径也扩大6倍，‎ 又因圆的面积=πr2，所以圆的面积扩大62=36倍；‎ 故选：B．‎ 点评： 此题主要考查圆的直径与半径的关系以及圆的面积的计算方法的灵活应用．‎ ‎　‎ ‎20．下面三幅图的阴影部分的面积相比较，（　　）的面积大．‎ ‎　 A． 图（1）大 B． 图（2）大 C． 图（3）大 D． 同样大 考点： 面积及面积的大小比较． ‎ 专题： 平面图形的认识与计算．‎ 分析： 三幅图，正方形的面积一样大．图（1）中，阴影的面积等于正方形的面积减去4个圆心角为90°的扇形的面积，而4个圆心角为90°的扇形的面积，就是一个圆的面积．‎ ‎（2）阴影的面积等于正方形的面积减去2个半圆的面积．2个半圆的面积就是一个圆的面积．‎ ‎（3）阴影的面积等于正方形的面积减去1个圆的面积．‎ 所以三幅图的阴影部分的面积都是正方形的面积减去圆的面积．‎ 解答： 解：三幅图的阴影部分的面积都是正方形的面积减去圆的面积，所以这三幅图的阴影部分的面积相等．‎ 故选：D．‎ 点评： 本题考查不规则图形面积的计算及大小比较．‎ ‎　‎ ‎21．如图，已知正方形面积是16平方分米，图中圆的面积是（　　）平方分米．‎ ‎　 A． 12.56 B． ‎6.28 ‎C． 50.24‎ 考点： 圆、圆环的面积． ‎ 专题： 平面图形的认识与计算．‎ 分析： 由题意可知：圆的半径是r，则正方形的边长是2r，因为正方形的面积是16平方分米，即2r×2r=16，则4r2=16，求出r2=4，求圆的面积，根据圆的面积=πr2，把r2=4代入即可得出结论．‎ 解答： 解：圆的半径是r，则正方形的边长是2r，‎ ‎2r×2r=16，‎ ‎ 4r2=16，‎ ‎ r2=4，‎ S=πr2=3.14×4=12.56（平方分米）；‎ 答：图中圆的面积是12.56平方分米；‎ 故选：A．‎ 点评： 求出r2=4是解答此题的关键；用到的知识点：正方形和圆的面积计算公式．‎ ‎　‎ 四、说说哪种做法简便．‎ ‎22．如图1，已知环形的外圆周长是18.84厘米，内圆周长是12.56厘米，环宽为1厘米，求环形面积．（两种方法求解）‎ 考点： 组合图形的面积． ‎ 专题： 平面图形的认识与计算．‎ 分析： 两种方法进行分析：解法一根据外圆面积减去内圆面积=环形面积，由此进行解答；‎ 解法二：先把圆环拉直，使它成为梯形，然后根据梯形面积计算公式进行解答．‎ 解答： 解：解法1　 用外圆面积减去内圆面积．‎ ‎3.14×（）2﹣3.14×（）2=15.7（平方厘米）‎ 解法2　 把圆环拉直，使它成为梯形，如图2．‎ ‎（18.84+12.56）×1÷2=15.7（平方厘米）‎ 答：阴影部分的面积是15.7平方厘米．‎ 点评： 此题考查了组合图形的面积，明确环形的面积和梯形面积计算公式，是解答此题的关键．‎ ‎　‎ ‎23．求如图1阴影部分面积，（单位：分米）（两种方法解答）‎ 考点： 组合图形的面积． ‎ 专题： 平面图形的认识与计算．‎ 分析： 本题可以两种方法进行分析：解法一：先求左边阴影部分面积，再求右边，然后相加；‎ 方法二：把原图进行转化，认真观察阴影部分正好是平行四边形的一半，然后根据阴影部分的面积等于和它等底等高的平行四边形面积的一半，由此解答即可．‎ 解答： 解：方法1　 先求左边阴影部分面积，再求右边，然后相加．‎ ‎3.14×42×﹣4×4÷2=4.56（平方分米）‎ ‎（4×4×2）×4÷2﹣3.14×42×=11.44（平方分米）‎ ‎11.44+4.56=16（平方分米）；‎ 方法2　 把原图进行转化，如图2．认真观察阴影部分正好是平行四边形的一半．‎ ‎4×（4×2）÷2=16（平方分米）‎ 答：阴影部分面积是16平方分米．‎ 点评： 明确阴影部分的面积可以由哪些图形的面积和或差求出，是解答此题的关键．‎ ‎　‎ 五、解答下面各题 ‎24．求出下面两图形的周长．（单位：厘米）‎ 考点： 圆、圆环的周长． ‎ 专题： 平面图形的认识与计算．‎ 分析： 根据圆的周长=πd，代入数据即可解答；‎ 图形的周长=πr+4r，代入数据即可解答．‎ 解答： 解：3.14×12=37.68（厘米）‎ 答：圆的周长是37.68厘米．‎ ‎3.14×5+5×4‎ ‎=15.7+20‎ ‎=35.7（厘米）‎ 答：图形的周长是35.7厘米．‎ 点评： 此题主要考查计算圆的周长和正方形周长的计算公式．‎ ‎　‎ ‎25．求出下面两图形阴影部分的面积．（单位：厘米）已知AC=CD=DB 考点： 组合图形的面积． ‎ 专题： 平面图形的认识与计算．‎ 分析： （1）左边图形中，阴影部分的面积=长方形的面积﹣半圆的面积，据此代入长方形和圆的面积公式即可求解；‎ ‎（2）阴影部分的面积=直径为4分米的圆的面积﹣直径为2厘米的圆的面积，利用圆的面积公式即可求解．‎ 解答： 解：（1）10×2×10﹣3.14×102÷2‎ ‎=200﹣3.14×50‎ ‎=200﹣157‎ ‎=43（平方厘米）‎ 答：阴影部分的面积是43平方厘米．‎ ‎（2）因为AC=CD=DB 所以AC=CD=DB=6÷3=2（厘米）‎ ‎3.14×22﹣3.14×（2÷2）2‎ ‎=12.56﹣3.14‎ ‎=9.42（平方厘米）‎ 答：阴影部分的面积是9.42平方厘米．‎ 点评： 明确阴影部分的面积由哪些图形的面积和或差求出，是解答此题的关键．‎ ‎　‎ ‎26．如图：一只青蛙从A到B有很多条路可走，其中走哪一条最近？任多少厘米？（单位：厘米） ‎ 考点： 直线、线段和射线的认识． ‎ 专题： 平面图形的认识与计算．‎ 分析： 因两点间线段最短，所以走直径最近．据此解答．‎ 解答： 解：2+2+2=6（厘米）‎ 答：走直径最近，长6厘米．‎ 点评： 本题主要考查了学生对两点间线段最短知识的运用．‎ ‎　‎ ‎27．一个圆环形跑道，如图，外沿的周长是‎31.4米，跑道的宽为‎2米，这个跑道要铺上沙子，每平方米需要沙子0.5吨，共需沙子多少吨？‎ 考点： 有关圆的应用题． ‎ 专题： 平面图形的认识与计算．‎ 分析： 根据题意，可利用圆的周长公式：C=2πr，计算出大圆的半径，圆环形跑道内小圆的半径为大圆半径减去环形跑道的宽，可根据圆的面积计算出大圆、小圆的面积各是多少，然后再用大圆的面积减去小圆的面积就是圆环的面积，再用圆环的面积乘0.5吨就是共需要的沙子，列式解答即可得到答案．‎ 解答： 解：大圆的半径为：314÷3.14÷2[来源:学+科+网]‎ ‎=100÷2‎ ‎=50（米）‎ 小圆的半径为：50﹣2=48（米）‎ 圆环的面积为：3.14×502﹣3.14×482‎ ‎=3.14×（2500﹣2304）‎ ‎=3.14×196‎ ‎=615.44（平方米）‎ 共有沙子：615.44×0.5=307.72（吨）‎ 答：共需沙子307.72吨．‎ 点评： 解答此题的关键是根据圆的面积公式计算出环形跑道的面积，然后再用环形跑道的面积乘0.5即可．‎ ‎　‎ ‎28．两个圆面积的和是31.4平方厘米，已知小圆周长是12.56厘米，求大圆的面积是多少平方厘米？‎ 考点： 圆、圆环的面积；圆、圆环的周长． ‎ 专题： 平面图形的认识与计算．‎ 分析： 先根据圆的周长公式，用小圆的周长除以3.14，再除以2，求出小圆的半径，再根据圆的面积公式求出小圆的面积，然后用大圆的面积减去小圆的面积即可．‎ 解答： 解：12.56÷3.14÷2=2（厘米）‎ ‎31.4﹣3.14×22‎ ‎=31.4﹣12.56‎ ‎=18.84（平方厘米）‎ 答：大圆的面积是18.84平方厘米．‎ 点评： 解决本题关键是熟记圆的周长和面积公式，C=2πr，S=πr2．‎ ‎　‎