安徽省合肥市一六八中学自主招生考试数学试题-Word版含答案 11页

www.ks5u.com 合肥168中学2017年面向全省自主招生考试《科学素养》测试数学试卷 一、 选择题（本大题共8小题，每小题5分，共40分）‎ 1、 已知 ， ，则二次根式 的值是（ ）‎ A、6 B、7 C、8 D、9‎ ‎2，有9张卡片，分别写有1～9这九个数字，将它们背面朝上洗匀后，任意抽取一张，记卡片上的数字为a，则使关于x的不等式组 有解的概率为（）‎ A、 B、 C、 D、 ‎ ‎3、已知一次函数 的图像经过点（3,0),且与坐标轴围成的三角形的面积为6，满足条件的函数有（ ）‎ A、2个 B、3个 C、4个 D、5个 ‎4、若实数 ，且 满足 .则 的值为（ ）‎ A、-20 B、2 C、2或20 D、2或20‎ ‎5、对于每个非零自然数，抛物线 以 表示这两点间的距离，则的值是（ ）‎ A、 B、 C、 D、 ‎ ‎6、已知是的三边，则下列式子一定正确的是（ ）‎ A、 B、 ‎ C、 D、 ‎ ‎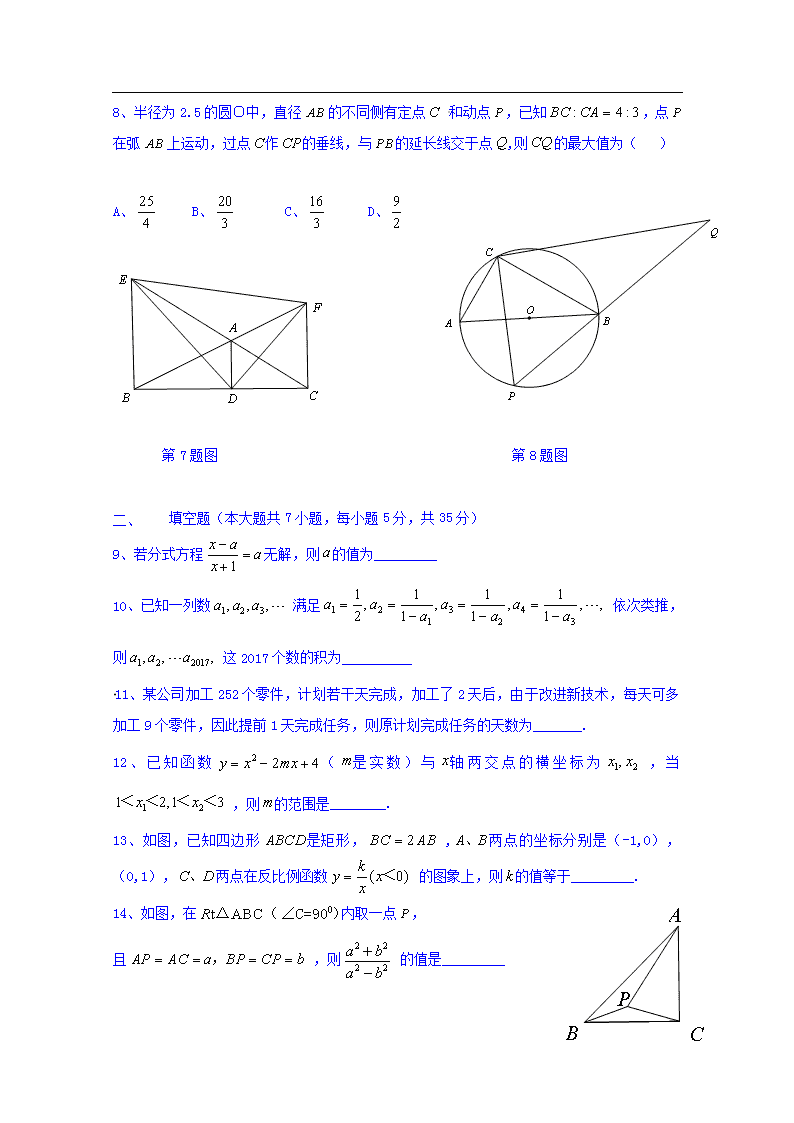7、如图，从各顶点作平行线 ，各与其对边或其延长线相交于 若 的面积为1，则的面积为（ ）‎ A、3 B、 C、 D、2‎ ‎8、半径为2.5的圆Ｏ中，直径的不同侧有定点 和动点，已知，点在弧上运动，过点作的垂线，与的延长线交于点,则的最大值为（ ）[来源:学,科,网]‎ A、 B、 C、 D、 ‎ ‎ 第7题图 第8题图 一、 填空题（本大题共7小题，每小题5分，共35分）‎ ‎9、若分式方程无解，则的值为_________‎ ‎10、已知一列数 满足 依次类推，则 这2017个数的积为__________‎ ‎11、某公司加工252个零件，计划若干天完成，加工了2天后，由于改进新技术，每天可多加工9个零件，因此提前1天完成任务，则原计划完成任务的天数为_______.‎ ‎12、已知函数（是实数）与轴两交点的横坐标为 ，当 ，则的范围是________.‎ ‎13、如图，已知四边形是矩形， ,两点的坐标分别是（-1,0），（0,1），两点在反比例函数 的图象上，则的值等于_________.‎ ‎14、如图，在内取一点，‎ 且 ，则 的值是_________[来源:Zxxk.Com]‎ ‎15、足球运动员在足球场上，常需要带球跑动到一定位置后，再进行射门，这个位置为射门点，射门点与球门边框两端点的夹角是射门角。如果点表示球门边框（不考虑球门的高度）的两端点，点表示射门点，连接 ，则就是射门角 在不考虑其他因素的情况下，一般地，射门角越大，射门进球的可能性越大。如图（1）（2）（3）是运动员带球跑动的三种常见的路线（用直线表示），则下列说法：‎ ①如图（1），,当运动员在线段的垂直平分线与的交点处射门，进球的可能性很大；‎ ②如图（2），垂足为,设，当运动员在离底线的距离为的点处（即 ）射门时，进球的可能性最大；‎ ③如图（3），与相交于点,设 的中点为 ，当点满足时，运动员在点处射门时，进球的可能性最大；‎ ④如图（3），过点作直线的垂线与线段的垂直平分线交于点，当点恰好是的外心时，运动员在点处射门时，进球的可能性最大.‎ ‎[来源:学科网]‎ 一、 解答题（本大题共6小题，共75分）‎ ‎16.(本题10分)‎ 若实数满足 求的值.‎ ‎[来源:Zxxk.Com]‎ ‎17.(本题12分)已知 试化简 ‎ ‎18.（本题13分）某学校在大课间举行跳绳活动，为此学校准备购置长、中、短三种跳绳若干，要求中跳绳的条数是长跳绳的2倍，且短跳绳的条数不超过长跳绳的6倍，已知长跳绳单价是20元，中跳绳的单价是15元，短跳绳的单价是8元。‎ ‎（1）若学校准备用不超过2300元的现金购买200条长、中、短跳绳，问学校有几种购买方案可供选择？‎ ‎（2）若学校准备恰好用3000元的现金购买条长、中、短跳绳.求的最大值.‎ ‎19.（本题13分）如图，四边形内接,是的直径，和相交于点,且 .‎ ‎（1）求证： ‎ ‎（2）分别延长交于点,若 求圆的半径.‎ ‎20.（本题13分）如图，在平面直角坐标系 中，为轴上两点，为轴上的两点，经过点的抛物线的一部分 与经过点 的抛物线的一部分组成一条封闭曲线，已知点的坐标为（0，-3），点是抛物线 的顶点.‎ ‎（1）求两点的坐标 ‎（2）在第四象限内是否存在一点，使得的面积最大？若存在，求出面积的最大值；若不存在，请说明理由；‎ ‎（3）当为直角三角形时，的值.‎ ‎21.(本题14分) 已知一个矩形纸片 ，将该纸片放置在平面直角坐标系中，点（11，0），点 （0，6），点为边上的动点（点 不与点重合），经过点折叠该纸片，得点 和折痕．设 ‎ ‎（1）如图①，当 时，求点的坐标；‎ ‎（2）如图②，经过点再次折叠纸片，使点落在直线上，得点和折痕 ，若，试用含有的式子表示；‎ ‎（3）在（2）的条件下，当点恰好落在边上时，求点的坐标．‎ ‎2017年学科素养考核数学试题参考答案 一、选择题（本大题共8小题，每小题5分，共40分）‎ ‎1-5 DBBAC，6-8 CDB 二、填空题（本大题共7小题，每小题5分，共35分）‎ ‎9、±1 10、 11、7 12、2＜m＜‎ ‎13、-6 14、 15、①②④‎ 三、共75分 ‎16、（10分）解：∵，∴a+b=168 ……3分 所以，‎ ‎∴ ……7分 解得：c=170 ……10分 ‎17、（12分）‎ 由得：x+2=a+， ……3分 ‎ ……8分 ‎∵，∴a≥1， ……10分 所以，原式= ……12分 ‎18、解：（1）设学校购买a条长跳绳，由题意得：‎ ‎ ……3分 解得： ……5分 ‎∵a为正整数，∴a的整数值为23,24,25,26‎ 所以学校共有4种购买方案可供选择． ……6分 ‎（2）设学校购买a条长跳绳，由题意得：‎ ‎ ……8分 化简得，得13a=4(375-n)， ……10分 ‎∴a为4的倍数，设为4k（k为整数），则n=375-13k，‎ ‎∴375-13k≤36k，‎ ‎∴，∴k的最小值为8，n的最大值为271． ……13分 ‎19、（1）证明：∵DC²=CE·CA，∴， ……3分 ‎△CDE∽△CAD，∴∠CDB=∠DBC，‎ ‎∴BC=CD； ……6分 ‎（2）解：如图，连接OC，‎ ‎∵BC=CD，∴∠DAC=∠CAB，‎ 又∵AO=CO，∴∠CAB=∠ACO，∴∠DAC=∠ACO，‎ ‎∴AD∥OC，∴， ……10分 ‎∵PB=OB，CD=，∴ ∴PC=‎ 又∵PC·PD=PB·PA 所以，半径OB=4 ……13分 ‎ ‎ ‎20、解：（1）y=mx²-2mx-3m=m(x-3)(x+1)，∵m≠0，‎ ‎∴当y=0时，，，∴A（-1,0），B（3,0）； ……2分 ‎（2）设：y=ax²+bx+c，‎ 将A、B、C三点的坐标代入得：‎ ‎，‎ 故：y=x²-2x-3 ……8分 如图：过点P作PQ∥y轴，交BC于Q，‎ 由B、C的坐标可得直线BC的解析式为：‎ y=x-3 ……5分 设P（a，a²-2a-3），Q（a，a-3）‎ ‎ ‎ 所以[来源:学_科_网]‎ 当时，有最大值为 此时，P（，） ……8分 ‎ ‎ ‎（3分）y=mx²-2mx-3m=m(x-1)²-4m，顶点M坐标（1，-4m），‎ 当x=0时，y=-3m，∴D（0，-3m），B（3，0），‎ ‎∴DM²=(0-1)²+(-3m+4m)²=m²+1,‎ MB²=(3-1)²+(0+4m)²=16m²+4，‎ BD²=(3-0)²+(0+3m)²=9m²+9， ……10分 当△BDM为Rt△时有：DM²+BD²=MB²或DM²+MB²=BD²．‎ ‎①DM²+BD²=MB²时有：m²+1+9m²+9=16m²+4，‎ 解得m=-1（∵m＜0，∴m=1舍去）； ‎ ‎②DM²+MB²=BD²时有：m²+1+16m²+4=19m²+9，‎ 解得m=（m=舍去）．‎ 综上，m=-1或时，△BDM为直角三角形． ……13分 ‎21、（1）（，6） ……2分 ‎（2）因为△OB＇P≌△OBP，△QC＇P≌△QCP ‎∴∠OPB＇=∠OPB，∠QPC＇=∠QPC，∴∠BOP=∠CPQ 所以△OBP≌△PCQ，∴ ……5分 由PC=11-t,CQ=6-m，得： ……7分 ‎（3）过P作PE⊥OA与点E 易得，△PC＇E∽△C＇QA∴‎ ‎∵PC＇=PC=11-t,PE=OB=6，AQ=m，=CQ=6-m ……9分 ‎，∴‎ 即：36-12m=t² ……12分 将代入得：‎ ‎3t²-22t+36=0，解得：，‎ 所以，点P的坐标为：（，6）或（，6） ……14分 ‎ ‎