中考数学模拟复习试卷9 6页

北京市东城区2011--2012学年第二学期初三综合练习（二）‎ 数 学 试 卷 考 生 须 知 ‎1.本试卷共5页，共五道大题，25道小题，满分120分.考试时间120分钟.‎ ‎2.在试卷和答题卡上认真填写学校名称、姓名和准考证号.‎ ‎3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效.‎ ‎4.在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答.‎ ‎5.考试结束，请将本试卷、答题卡一并交回.‎ 一、选择题（本题共32分，每小题4分）‎ 下面各题均有四个选项，其中只有一个是符合题意的. ‎ ‎1. 9的算术平方根是 ‎ A．-9 B．‎9　‎ 　 　C．3　　　　 D．±3‎ ‎2. 如图，由几个小正方体组成的立体图形的俯视图是 ‎3. 下列运算正确的是 ‎ A． B． C． D．‎ ‎4. 抛掷一枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，掷得朝上一面的点数为奇数的概率为 A． B． C． D． ‎ ‎5. 如果一个多边形的内角和是其外角和的2倍，那么这个多边形是 ‎ A．六边形 B．五边形 C．四边形 D．三角形 ‎6. 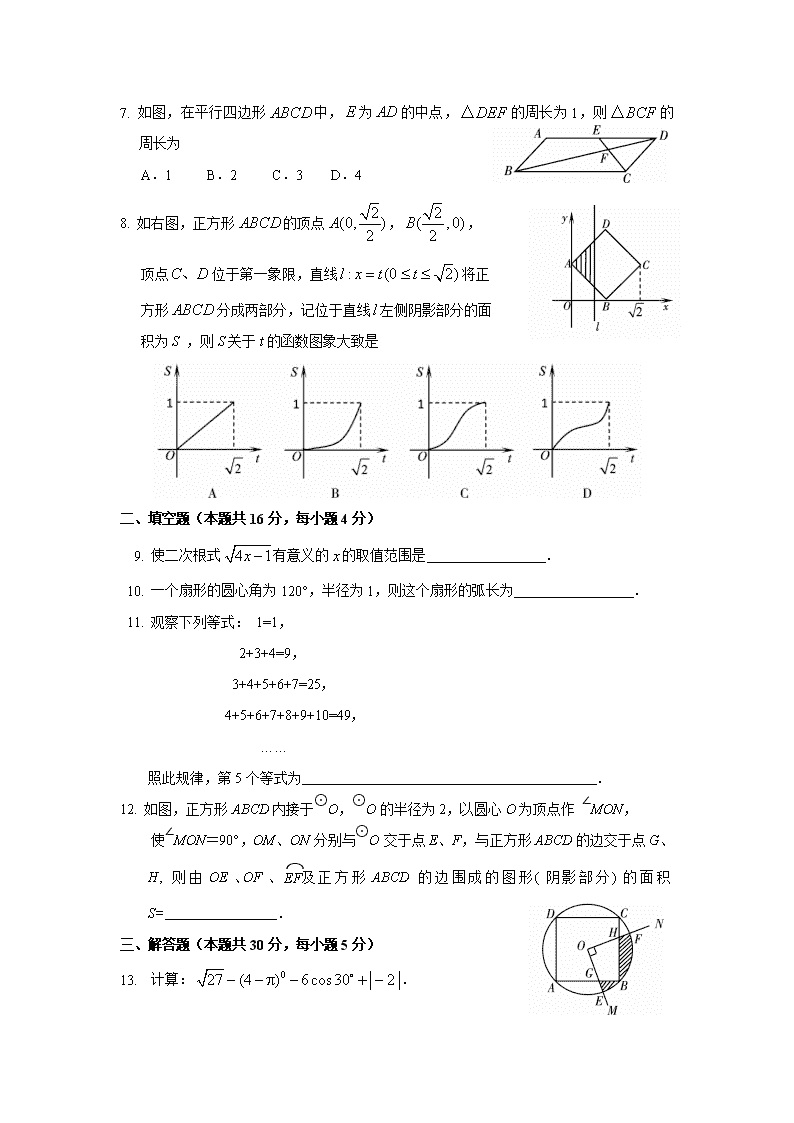在社会实践活动中，某同学对甲、乙、丙、丁四个城市一至五月份的香蕉价格进行调查．四个城市5个月香蕉价格的平均值均为3.50元，方差分别为＝18.3，＝17.4，＝20.1，＝12.5．一至五月份香蕉价格最稳定的城市是 ‎ A．甲 B．乙 C．丙 D．丁 ‎7. 如图，在平行四边形中，为的中点，的周长为1，则的周长为 A．1 B．2 C．3 D．4‎ ‎8. 如右图，正方形的顶点，，‎ 顶点位于第一象限，直线将正 方形分成两部分，记位于直线左侧阴影部分的面 积为S ，则S关于t的函数图象大致是 ‎ 二、填空题（本题共16分，每小题4分）‎ ‎ 9. 使二次根式有意义的的取值范围是 ．‎ ‎ 10. 一个扇形的圆心角为120°，半径为1，则这个扇形的弧长为 ．‎ ‎ 11. 观察下列等式： 1=1，‎ ‎2+3+4=9，‎ ‎3+4+5+6+7=25，‎ ‎4+5+6+7+8+9+10=49，‎ ‎……‎ 照此规律，第5个等式为 ．‎ ‎12. 如图，正方形ABCD内接于⊙O，⊙O的半径为2，以圆心O为顶点作 ∠MON，‎ ‎ 使∠MON＝90°，OM、ON分别与⊙O交于点E、F，与正方形ABCD的边交于点G、H, 则由OE、OF、及正方形ABCD的边围成的图形(阴影部分)的面积S= ．‎ 三、解答题（本题共30分，每小题5分）‎ ‎13. 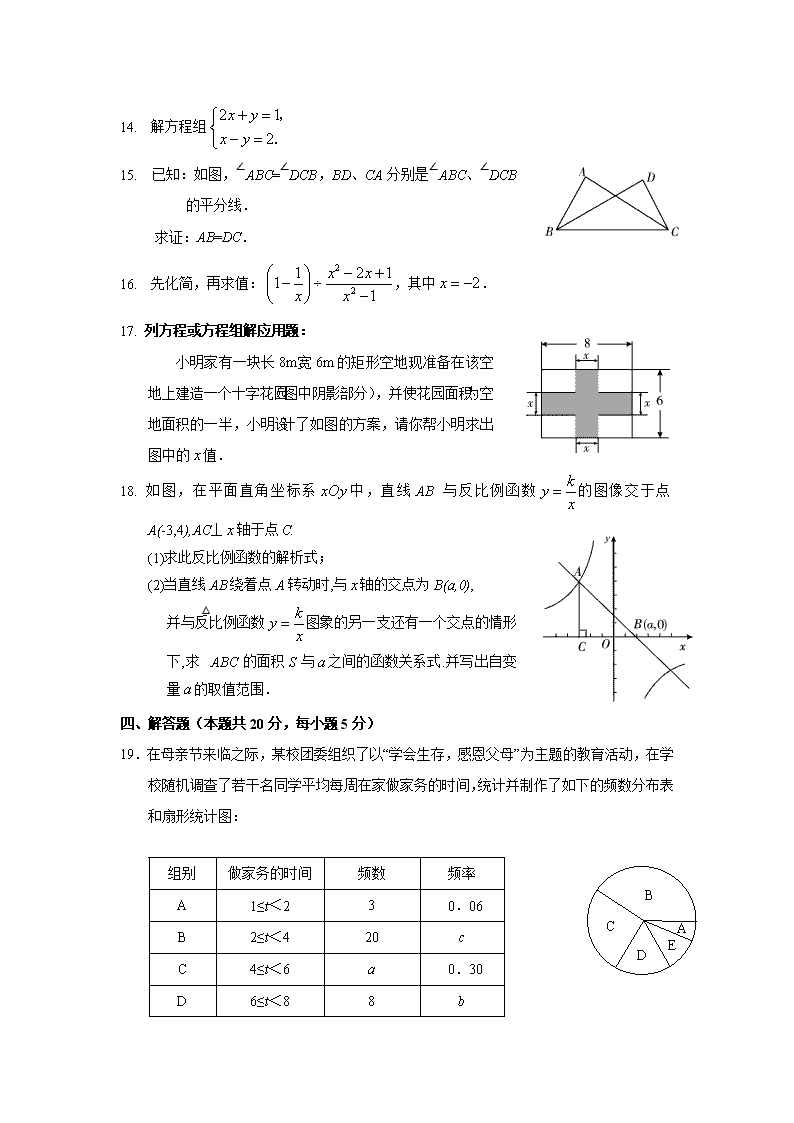计算：．‎ ‎14. 解方程组 ‎15. 已知：如图，∠ABC=∠DCB，BD、CA分别是∠ABC、∠DCB 的平分线．‎ 求证：AB=DC．‎ ‎16. 先化简，再求值：，其中．‎ ‎17. 列方程或方程组解应用题：‎ 小明家有一块长8m、宽6m的矩形空地，现准备在该空地上建造一个十字花园（图中阴影部分），并使花园面积为空地面积的一半，小明设计了如图的方案，请你帮小明求出图中的值．‎ ‎18. 如图，在平面直角坐标系中，直线AB与反比例函数的图像交于点A(-3,4),AC⊥轴于点C. ‎ ‎(1)求此反比例函数的解析式；‎ ‎(2)当直线AB绕着点A转动时,与轴的交点为B(a,0), ‎ 并与反比例函数图象的另一支还有一个交点的情形下,求△ABC的面积S与之间的函数关系式.并写出自变量的取值范围．‎ 四、解答题（本题共20分，每小题5分）‎ ‎19．在母亲节来临之际，某校团委组织了以“学会生存，感恩父母”为主题的教育活动，在学校随机调查了若干名同学平均每周在家做家务的时间，统计并制作了如下的频数分布表和扇形统计图：‎ 组别 做家务的时间 频数 B C E A D 频率 A ‎1≤t＜2‎ ‎3‎ ‎ 0．06‎ B ‎2≤t＜4‎ ‎20‎ c C ‎4≤t＜6‎ a ‎ 0．30‎ D ‎6≤t＜8‎ ‎8‎ b E t≥8‎ ‎4‎ ‎ 0．08‎ ‎ 根据上述信息回答下列问题：‎ ‎（1）a= ，b= ; ww w .xkb1 .c om ‎（2）在扇形统计图中，B组所占圆心角的度数为 ;‎ ‎（3）全校共有1000名学生，估计该校平均每周做家务时间不少于4小时的学生约有多少人？‎ ‎20． 如图，在平行四边形中，，，于点，，求的值． ‎ ‎21．如图，在矩形ABCD中，点O在对角线AC上，以OA长为 ‎ 半径的与AD，AC分别交于点E，F，∠ACB=∠DCE ．‎ ‎（1）请判断直线CE与的位置关系，并证明你的结论；‎ ‎（2）若 DE:EC=1：, ，求⊙O的半径．‎ ‎22. 阅读并回答问题：‎ ‎ 小亮是一位刻苦学习、勤于思考、勇于创新的同学．一天他在解方程时，突发奇想：在实数范围内无解，如果存在一个数i，使，那么当时，有i，从而i是方程的两个根．‎ 据此可知：(1) i可以运算，例如：i3=i2·i=-1×i=-i，则i4= ，‎ ‎ i2011=______________，i2012=__________________；‎ ‎(2)方程的两根为 （根用i表示）．‎ 五．解答题（本题共22分，第23题7分，第24题7分，第25题8分）‎ ‎23. 已知关于的方程．新课 标 第一 网 ‎（1） 若方程有两个不相等的实数根，求的取值范围；‎ ‎（2） 若正整数满足，设二次函数的图象与 轴交于两点，将此图象在x轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象．请你结合这个新的图象回答：当直线与此图象恰好有三个公共点时，求出的值（只需要求出两个满足题意的k值即可）．‎ ‎24. 已知：等边中，点O是边AC,BC的垂直平分线的交点，M,N分别在直线AC, BC 上，且．‎ ‎(1) 如图1，当CM=CN时， M、N分别在边AC、BC上时，请写出AM、CN 、MN三者之间的数量关系；‎ ‎（2） 如图2，当CM≠CN时，M、N分别在边AC、BC上时，（1）中的结论是否仍然成立？若成立，请你加以证明；若不成立，请说明理由；‎ ‎(3) 如图3，当点M在边AC上，点N在BC 的延长线上时，请直接写出线段AM、CN 、MN三者之间的数量关系．‎ ‎25．如图，在平面直角坐标系中，已知二次函数的图像与轴交于点，与轴交于A、B两点，点B的坐标为 ‎（1） 求二次函数的解析式及顶点D的坐标；‎ ‎（2） 点M是第二象限内抛物线上的一动点，若直线OM把四边形ACDB分成面积为1:2的两部分，求出此时点的坐标；‎ ‎（3） 点P是第二象限内抛物线上的一动点，问：点P在何处时△‎ 的面积最大？最大面积是多少？并求出 此时点P的坐标.‎ ‎ ‎