中考数学试题分类汇编考点32：尺规作图 39页

中考数学试题分类汇编：考点 32 尺规作图 一．选择题（共 13 小题） 1．（2018•襄阳）如图，在△ABC 中，分别以点 A 和点 C 为圆心，大于 AC 长 为半径画弧，两弧相交于点 M，N，作直线 MN 分别交 BC，AC 于点 D，E．若 AE=3cm，△ABD 的周长为 13cm，则△ABC 的周长为（ ） A．16cm B．19cm C．22cm D．25cm 【分析】利用线段的垂直平分线的性质即可解决问题． 【解答】解：∵DE 垂直平分线段 AC， ∴DA=DC，AE=EC=6cm， ∵AB+AD+BD=13cm， ∴AB+BD+DC=13cm， ∴△ABC 的周长=AB+BD+BC+AC=13+6=19cm， 故选：B． 2．（2018•河北）尺规作图要求：Ⅰ、过直线外一点作这条直线的垂线；Ⅱ、作 线段的垂直平分线； Ⅲ、过直线上一点作这条直线的垂线；Ⅳ、作角的平分线． 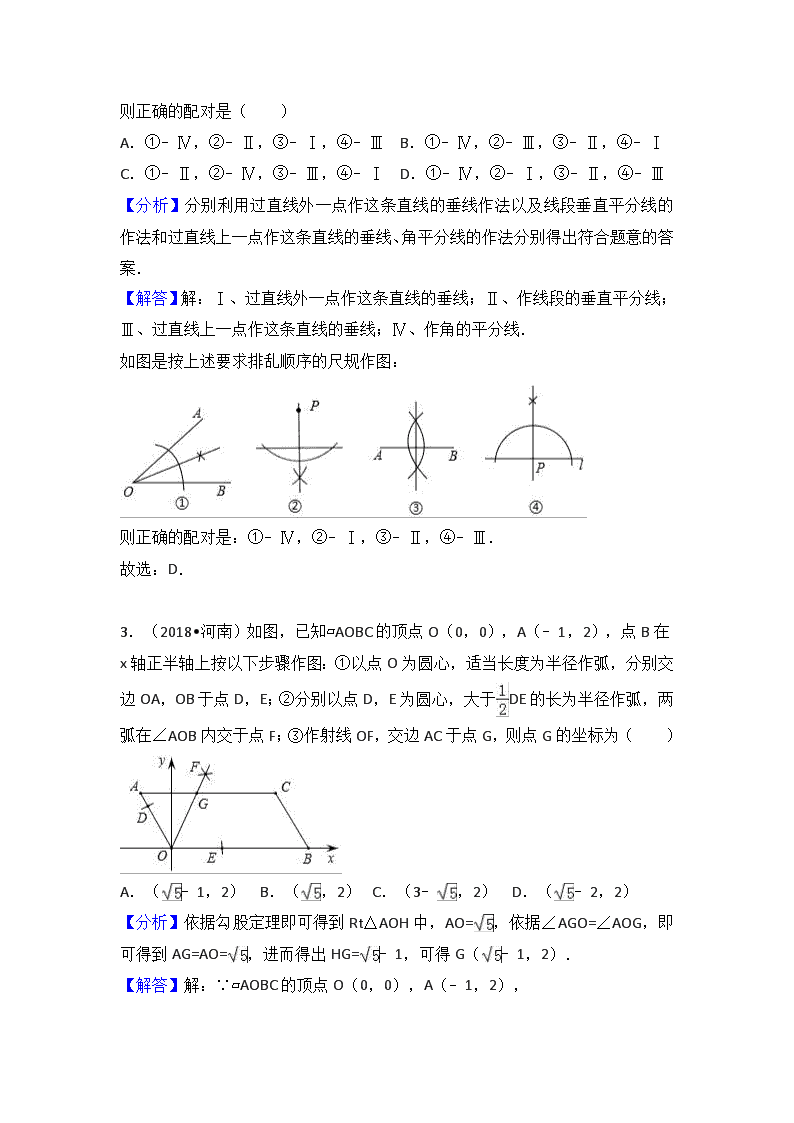如图是按上述要求排乱顺序的尺规作图： 则正确的配对是（ ） A．①﹣Ⅳ，②﹣Ⅱ，③﹣Ⅰ，④﹣Ⅲ B．①﹣Ⅳ，②﹣Ⅲ，③﹣Ⅱ，④﹣Ⅰ C．①﹣Ⅱ，②﹣Ⅳ，③﹣Ⅲ，④﹣Ⅰ D．①﹣Ⅳ，②﹣Ⅰ，③﹣Ⅱ，④﹣Ⅲ 【分析】分别利用过直线外一点作这条直线的垂线作法以及线段垂直平分线的作 法和过直线上一点作这条直线的垂线、角平分线的作法分别得出符合题意的答 案． 【解答】解：Ⅰ、过直线外一点作这条直线的垂线；Ⅱ、作线段的垂直平分线； Ⅲ、过直线上一点作这条直线的垂线；Ⅳ、作角的平分线． 如图是按上述要求排乱顺序的尺规作图： 则正确的配对是：①﹣Ⅳ，②﹣Ⅰ，③﹣Ⅱ，④﹣Ⅲ． 故选：D． 3．（2018•河南）如图，已知▱ AOBC 的顶点 O（0，0），A（﹣1，2），点 B 在 x 轴正半轴上按以下步骤作图：①以点 O 为圆心，适当长度为半径作弧，分别 交边 OA，OB 于点 D，E；②分别以点 D，E 为圆心，大于 DE 的长为半径作弧， 两弧在∠AOB 内交于点 F；③作射线 OF，交边 AC 于点 G，则点 G 的坐标为（ ） A．（ ﹣1，2） B．（ ，2） C．（3﹣ ，2） D．（ ﹣2，2） 【分析】依据勾股定理即可得到 Rt△AOH 中，AO= ，依据∠AGO=∠AOG，即 可得到 AG=AO= ，进而得出 HG= ﹣1，可得 G（ ﹣1，2）． 【解答】解：∵▱ AOBC 的顶点 O（0，0），A（﹣1，2）， ∴AH=1，HO=2， ∴Rt△AOH 中，AO= ， 由题可得，OF 平分∠AOB， ∴∠AOG=∠EOG， 又∵AG∥OE， ∴∠AGO=∠EOG， ∴∠AGO=∠AOG， ∴AG=AO= ， ∴HG= ﹣1， ∴G（ ﹣1，2）， 故选：A． 4．（2018•宜昌）尺规作图：经过已知直线外一点作这条直线的垂线，下列作图 中正确的是（ ） A． B． C． D． 【分析】根据过直线外一点向直线作垂线即可． 【解答】已知：直线 AB 和 AB 外一点 C． 求作：AB 的垂线，使它经过点 C． 作法：（1）任意取一点 K，使 K 和 C 在 AB 的两旁． （2）以 C 为圆心，CK 的长为半径作弧，交 AB 于点 D 和 E． （3）分别以 D 和 E 为圆心，大于 DE 的长为半径作弧，两弧交于点 F， （4）作直线 CF． 直线 CF 就是所求的垂线． 故选：B． 5．（2018•潍坊）如图，木工师傅在板材边角处作直角时，往往使用“三弧法”， 其作法是： （1）作线段 AB，分别以 A，B 为圆心，以 AB 长为半径作弧，两弧的交点为 C； （2）以 C 为圆心，仍以 AB 长为半径作弧交 AC 的延长线于点 D； （3）连接 BD，BC． 下列说法不正确的是（ ） A．∠CBD=30° B．S△BDC= AB2 C．点 C 是△ABD 的外心 D．sin2A+cos2D=1 【分析】根据等边三角形的判定方法，直角三角形的判定方法以及等边三角形的 性质，直角三角形的性质一一判断即可； 【解答】解：由作图可知：AC=AB=BC， ∴△ABC 是等边三角形， 由作图可知：CB=CA=CD， ∴点 C 是△ABD 的外心，∠ABD=90°， BD= AB， ∴S△ABD= AB2， ∵AC=CD， ∴S△BDC= AB2， 故 A、B、C 正确， 故选：D． 6．（2018•郴州）如图，∠AOB=60°，以点 O 为圆心，以任意长为半径作弧交 OA，OB 于 C，D 两点；分别以 C，D 为圆心，以大于 CD 的长为半径作弧，两 弧相交于点 P；以 O 为端点作射线 OP，在射线 OP 上截取线段 OM=6，则 M 点 到 OB 的距离为（ ） A．6 B．2 C．3 D． 【分析】直接利用角平分线的作法得出 OP 是∠AOB 的角平分线，再利用直角三 角形的性质得出答案． 【解答】解：过点 M 作 ME⊥OB 于点 E， 由题意可得：OP 是∠AOB 的角平分线， 则∠POB= ×60°=30°， ∴ME= OM=3． 故选：C． 7．（2018•台州）如图，在▱ ABCD 中，AB=2，BC=3．以点 C 为圆心，适当长为 半径画弧，交 BC 于点 P，交 CD 于点 Q，再分别以点 P，Q 为圆心，大于 PQ 的 长为半径画弧，两弧相交于点 N，射线 CN 交 BA 的延长线于点 E，则 AE 的长是 （ ） A． B．1 C． D． 【分析】只要证明 BE=BC 即可解决问题； 【解答】解：∵由题意可知 CF 是∠BCD 的平分线， ∴∠BCE=∠DCE． ∵四边形 ABCD 是平行四边形， ∴AB∥CD， ∴∠DCE=∠E，∠BCE=∠AEC， ∴BE=BC=3， ∵AB=2， ∴AE=BE﹣AB=1， 故选：B． 8．（2018•嘉兴）用尺规在一个平行四边形内作菱形 ABCD，下列作法中错误的 是（ ） A． B． C． D． 【分析】根据菱形的判定和作图根据解答即可． 【解答】解：A、由作图可知，AC⊥BD，且平分 BD，即对角线平分且垂直的四 边形是菱形，正确； B、由作图可知 AB=BC，AD=AB，即四边相等的四边形是菱形，正确； C、由作图可知 AB=DC，AD=BC，只能得出 ABCD 是平行四边形，错误； D、由作图可知对角线 AC 平分对角，可以得出是菱形，正确； 故选：C． 9．（2018•昆明）如图，点 A 在双曲线 y═ （x＞0）上，过点 A 作 AB⊥x 轴， 垂足为点 B，分别以点 O 和点 A 为圆心，大于 OA 的长为半径作弧，两弧相交 于 D，E 两点，作直线 DE 交 x 轴于点 C，交 y 轴于点 F（0，2），连接 AC．若 AC=1，则 k 的值为（ ） A．2 B． C． D． 【分析】如图，设 OA 交 CF 于 K．利用面积法求出 OA 的长，再利用相似三角形 的性质求出 AB、OB 即可解决问题； 【解答】解：如图，设 OA 交 CF 于 K． 由作图可知，CF 垂直平分线段 OA， ∴OC=CA=1，OK=AK， 在 Rt△OFC 中，CF= = ， ∴AK=OK= = ， ∴OA= ， 由△FOC∽△OBA，可得 = = ， ∴ = = ， ∴OB= ，AB= ， ∴A（ ， ）， ∴k= ． 故选：B． 10．（2018•湖州）尺规作图特有的魅力曾使无数人沉湎其中．传说拿破仑通过 下列尺规作图考他的大臣： ①将半径为 r 的⊙O 六等分，依次得到 A，B，C，D，E，F 六个分点； ②分别以点 A，D 为圆心，AC 长为半径画弧，G 是两弧的一个交点； ③连结 OG． 问：OG 的长是多少？ 大臣给出的正确答案应是（ ） A． r B．（1+ ）r C．（1+ ）r D． r 【分析】如图连接 CD，AC，DG，AG．在直角三角形即可解决问题； 【解答】解：如图连接 CD，AC，DG，AG． ∵AD 是⊙O 直径， ∴∠ACD=90°， 在 Rt△ACD 中，AD=2r，∠DAC=30°， ∴AC= r， ∵DG=AG=CA，OD=OA， ∴OG⊥AD， ∴∠GOA=90°， ∴OG= = = r， 故选：D． 11．（2018•台湾）如图，锐角三角形 ABC 中，BC＞AB＞AC，甲、乙两人想找一 点 P，使得∠BPC 与∠A 互补，其作法分别如下： （甲）以 A 为圆心，AC 长为半径画弧交 AB 于 P 点，则 P 即为所求； （乙）作过 B 点且与 AB 垂直的直线 l，作过 C 点且与 AC 垂直的直线，交 l 于 P 点，则 P 即为所求 对于甲、乙两人的作法，下列叙述何者正确？（ ） A．两人皆正确 B．两人皆错误 C．甲正确，乙错误 D．甲错误，乙正确 【分析】甲：根据作图可得 AC=AP，利用等边对等角得：∠APC=∠ACP，由平角 的定义可知：∠BPC+∠APC=180°，根据等量代换可作判断； 乙：根据四边形的内角和可得：∠BPC+∠A=180°． 【解答】解：甲：如图 1，∵AC=AP， ∴∠APC=∠ACP， ∵∠BPC+∠APC=180° ∴∠BPC+∠ACP=180°， ∴甲错误； 乙：如图 2，∵AB⊥PB，AC⊥PC， ∴∠ABP=∠ACP=90°， ∴∠BPC+∠A=180°， ∴乙正确， 故选：D． 12．（2018•安顺）已知△ABC（AC＜BC），用尺规作图的方法在 BC 上确定一点 P，使 PA+PC=BC，则符合要求的作图痕迹是 （ ） A． B ． C． D． 【分析】利用线段垂直平分线的性质以及圆的性质分别分得出即可． 【解答】解：A、如图所示：此时 BA=BP，则无法得出 AP=BP，故不能得出 PA+PC=BC， 故此选项错误； B、如图所示：此时 PA=PC，则无法得出 AP=BP，故不能得出 PA+PC=BC，故此选 项错误； C、如图所示：此时 CA=CP，则无法得出 AP=BP，故不能得出 PA+PC=BC，故此选 项错误； D、如图所示：此时 BP=AP，故能得出 PA+PC=BC，故此选项正确； 故选：D． 13．（2017•南宁）如图，△ABC 中，AB＞AC，∠CAD 为△ABC 的外角，观察图 中尺规作图的痕迹，则下列结论错误的是（ ） A．∠DAE=∠B B．∠EAC=∠C C．AE∥BC D．∠DAE=∠EAC 【分析】根据图中尺规作图的痕迹，可得∠DAE=∠B，进而判定 AE∥BC，再根 据平行线的性质即可得出结论． 【解答】解：根据图中尺规作图的痕迹，可得∠DAE=∠B，故 A 选项正确， ∴AE∥BC，故 C 选项正确， ∴∠EAC=∠C，故 B 选项正确， ∵AB＞AC， ∴∠C＞∠B， ∴∠CAE＞∠DAE，故 D 选项错误， 故选：D． 二．填空题（共 7 小题） 14．（2018•南京）如图，在△ABC 中，用直尺和圆规作 AB、AC 的垂直平分线， 分别交 AB、AC 于点 D、E，连接 DE．若 BC=10cm，则 DE= 5 cm． 【分析】直接利用线段垂直平分线的性质得出 DE 是△ABC 的中位线，进而得出 答案． 【解答】解：∵用直尺和圆规作 AB、AC 的垂直平分线， ∴D 为 AB 的中点，E 为 AC 的中点， ∴DE 是△ABC 的中位线， ∴DE= BC=5cm． 故答案为：5． 15．（2018•淮安）如图，在 Rt△ABC 中，∠C=90°，AC=3，BC=5，分别以点 A、 B 为圆心，大于 AB 的长为半径画弧，两弧交点分别为点 P、Q，过 P、Q 两点作 直线交 BC 于点 D，则 CD 的长是 ． 【分析】连接 AD 由 PQ 垂直平分线段 AB，推出 DA=DB，设 DA=DB=x，在 Rt△ACD 中，∠C=90°，根据 AD2=AC2+CD2 构建方程即可解决问题； 【解答】解：连接 AD． ∵PQ 垂直平分线段 AB， ∴DA=DB，设 DA=DB=x， 在 Rt△ACD 中，∠C=90°，AD2=AC2+CD2， ∴x2=32+（5﹣x）2， 解得 x= ， ∴CD=BC﹣DB=5﹣ = ， 故答案为 ． 16．（2018•山西）如图，直线 MN∥PQ，直线 AB 分别与 MN，PQ 相交于点 A， B．小宇同学利用尺规按以下步骤作图：①以点 A 为圆心，以任意长为半径作弧 交 AN 于点 C，交 AB 于点 D；②分别以 C，D 为圆心，以大于 CD 长为半径作弧， 两弧在∠NAB 内交于点 E；③作射线 AE 交 PQ 于点 F．若 AB=2，∠ABP=60°，则 线段 AF 的长为 2 ． 【分析】作高线 BG，根据直角三角形 30 度角的性质得：BG=1，AG= ，可得 AF 的长． 【解答】解：∵MN∥PQ， ∴∠NAB=∠ABP=60°， 由题意得：AF 平分∠NAB， ∴∠1=∠2=30°， ∵∠ABP=∠1+∠3， ∴∠3=30°， ∴∠1=∠3=30°， ∴AB=BF，AG=GF， ∵AB=2， ∴BG= AB=1， ∴AG= ， ∴AF=2AG=2 ， 故答案为：2 ． 17．（2018•东营）如图，在 Rt△ABC 中，∠B=90°，以顶点 C 为圆心，适当长为 半径画弧，分别交 AC，BC 于点 E，F，再分别以点 E，F 为圆心，大于 EF 的长 为半径画弧，两弧交于点 P，作射线 CP 交 AB 于点 D．若 BD=3，AC=10，则△ACD 的面积是 15 ． 【分析】作 DQ⊥AC，由角平分线的性质知 DB=DQ=3，再根据三角形的面积公式 计算可得． 【解答】解：如图，过点 D 作 DQ⊥AC 于点 Q， 由作图知 CP 是∠ACB 的平分线， ∵∠B=90°，BD=3， ∴DB=DQ=3， ∵AC=10， ∴S△ACD= •AC•DQ= ×10×3=15， 故答案为：15． 18．（2018•通辽）如图，在△ABC 中，按以下步骤作图：①分别以点 A 和点 C 为圆心，以大于 AC 的长为半径作弧，两弧相交于 M、N 两点；②作直线 MN 交 BC 于点 D，连接 AD．若 AB=BD，AB=6，∠C=30°，则△ACD 的面积为 9 ． 【分析】只要证明△ABD 是等边三角形，推出 BD=AD=DC，可得 S△ADC=S△ABD 即可 解决问题； 【解答】解：由作图可知，MN 垂直平分线段 AC， ∴DA=DC， ∴∠C=∠DAC=30°， ∴∠ADB=∠C+∠DAC=60°， ∵AB=AD， ∴△ABD 是等边三角形， ∴BD=AD=DC， ∴S△ADC=S△ABD= ×62=9 ， 故答案为 9 ． 19．（2018•成都）如图，在矩形 ABCD 中，按以下步骤作图：①分别以点 A 和 C 为圆心，以大于 AC 的长为半径作弧，两弧相交于点 M 和 N；②作直线 MN 交 CD 于点 E．若 DE=2，CE=3，则矩形的对角线 AC 的长为 ． 【分析】连接 AE，如图，利用基本作图得到 MN 垂直平分 AC，则 EA=EC=3，然 后利用勾股定理先计算出 AD，再计算出 AC． 【解答】解：连接 AE，如图， 由作法得 MN 垂直平分 AC， ∴EA=EC=3， 在 Rt△ADE 中，AD= = ， 在 Rt△ADC 中，AC= = ． 故答案为 ． 20．（2018•湖州）在每个小正方形的边长为 1 的网格图形中，每个小正方形的 顶点称为格点．以顶点都是格点的正方形 ABCD 的边为斜边，向内作四个全等的 直角三角形，使四个直角顶点 E，F，G，H 都是格点，且四边形 EFGH 为正方形， 我们把这样的图形称为格点弦图．例如，在如图 1 所示的格点弦图中，正方形 ABCD 的边长为 ，此时正方形 EFGH 的而积为 5．问：当格点弦图中的正方形 ABCD 的边长为 时，正方形 EFGH 的面积的所有可能值是 13 或 49 或 9 （不 包括 5）． 【分析】当 DG= ，CG=2 时，满足 DG2+CG2=CD2，此时 HG= ，可得正 方形 EFGH 的面积为 13．当 DG=8，CG=1 时，满足 DG2+CG2=CD2，此时 HG=7， 可得正方形 EFGH 的面积为 49．当 DG=7，CG=4 时，满足 DG2+CG2=CD2，此时 HG=3， 可得正方形 EFGH 的面积为 9． 【解答】解：当 DG= ，CG=2 时，满足 DG2+CG2=CD2，此时 HG= ，可 得正方形 EFGH 的面积为 13． 当 DG=8，CG=1 时，满足 DG2+CG2=CD2，此时 HG=7，可得正方形 EFGH 的面积为 49． 当 DG=7，CG=4 时，满足 DG2+CG2=CD2，此时 HG=3，可得正方形 EFGH 的面积为 9． 故答案为 13 或 49 或 9． 三．解答题（共 21 小题） 21．（2018•广州）如图，在四边形 ABCD 中，∠B=∠C=90°，AB＞CD，AD=AB+CD． （1）利用尺规作∠ADC 的平分线 DE，交 BC 于点 E，连接 AE（保留作图痕迹， 不写作法）； （2）在（1）的条件下， ①证明：AE⊥DE； ②若 CD=2，AB=4，点 M，N 分别是 AE，AB 上的动点，求 BM+MN 的最小值． 【分析】（1）利用尺规作出∠ADC 的角平分线即可； （2）①延长 DE 交 AB 的延长线于 F．只要证明 AD=AF，DE=EF，利用等腰三角形 三线合一的性质即可解决问题； ②作点 B 关于 AE 的对称点 K，连接 EK，作 KH⊥AB 于 H，DG⊥AB 于 G．连接 MK．由 MB=MK，推出 MB+MN=KM+MN，根据垂线段最短可知：当 K、M、N 共 线，且与 KH 重合时，KM+MN 的值最小，最小值为 KH 的长； 【解答】解：（1）如图，∠ADC 的平分线 DE 如图所示． （2）①延长 DE 交 AB 的延长线于 F． ∵CD∥AF， ∴∠CDE=∠F，∵∠CDE=∠ADE， ∴∠ADF=∠F， ∴AD=AF， ∵AD=AB+CD=AB+BF， ∴CD=BF， ∵∠DEC=∠BEF， ∴△DEC≌△FEB， ∴DE=EF， ∵AD=AF， ∴AE⊥DE． ②作点 B 关于 AE 的对称点 K，连接 EK，作 KH⊥AB 于 H，DG⊥AB 于 G．连接 MK． ∵AD=AF，DE=EF， ∴AE 平分∠DAF，则△AEK≌△AEB， ∴AK=AB=4， 在 Rt△ADG 中，DG= =4 ， ∵KH∥DG， ∴ = ， ∴ = ， ∴KH= ， ∵MB=MK， ∴MB+MN=KM+MN， ∴当 K、M、N 共线，且与 KH 重合时，KM+MN 的值最小，最小值为 KH 的长， ∴BM+MN 的最小值为 ． 22．（2018•广东）如图，BD 是菱形 ABCD 的对角线，∠CBD=75°， （1）请用尺规作图法，作 AB 的垂直平分线 EF，垂足为 E，交 AD 于 F；（不要 求写作法，保留作图痕迹） （2）在（1）条件下，连接 BF，求∠DBF 的度数． 【分析】（1）分别以 A、B 为圆心，大于 AB 长为半径画弧，过两弧的交点作 直线即可； （2）根据∠DBF=∠ABD﹣∠ABF 计算即可； 【解答】解：（1）如图所示，直线 EF 即为所求； （2）∵四边形 ABCD 是菱形， ∴∠ABD=∠DBC= ∠ABC=75°，DC∥AB，∠A=∠C． ∴∠ABC=150°，∠ABC+∠C=180°， ∴∠C=∠A=30°， ∵EF 垂直平分线线段 AB， ∴AF=FB， ∴∠A=∠FBA=30°， ∴∠DBF=∠ABD﹣∠FBE=45°． 23．（2018•安徽）如图，⊙O 为锐角△ABC 的外接圆，半径为 5． （1）用尺规作图作出∠BAC 的平分线，并标出它与劣弧 的交点 E（保留作图 痕迹，不写作法）； （2）若（1）中的点 E 到弦 BC 的距离为 3，求弦 CE 的长． 【分析】（1）利用基本作图作 AE 平分∠BAC； （2）连接 OE 交 BC 于 F，连接 OC，如图，根据圆周角定理得到 = ，再根据 垂径定理得到 OE⊥BC，则 EF=3，OF=2，然后在 Rt△OCF 中利用勾股定理计算出 CF= ，在 Rt△CEF 中利用勾股定理可计算出 CE． 【解答】解：（1）如图，AE 为所作； （2）连接 OE 交 BC 于 F，连接 OC，如图， ∵AE 平分∠BAC， ∴∠BAE=∠CAE， ∴ = ， ∴OE⊥BC， ∴EF=3， ∴OF=5﹣3=2， 在 Rt△OCF 中，CF= = ， 在 Rt△CEF 中，CE= = ． 24．（2018•自贡）如图，在△ABC 中，∠ACB=90°． （1）作出经过点 B，圆心 O 在斜边 AB 上且与边 AC 相切于点 E 的⊙O（要求： 用尺规作图，保留作图痕迹，不写作法和证明） （2）设（1）中所作的⊙O 与边 AB 交于异于点 B 的另外一点 D，若⊙O 的直径 为 5，BC=4；求 DE 的长．（如果用尺规作图画不出图形，可画出草图完成（2） 问） 【分析】（1）作∠ABC 的角平分线交 AC 于 E，作 EO⊥AC 交 AB 于点 O，以 O 为圆心，OB 为半径画圆即可解决问题； （2）作 OH⊥BC 于 H．首先求出 OH、EC、BE，利用△BCE∽△BED，可得 = ， 解决问题； 【解答】解：（1）⊙O 如图所示； （2）作 OH⊥BC 于 H． ∵AC 是⊙O 的切线， ∴OE⊥AC， ∴∠C=∠CEO=∠OHC=90°， ∴四边形 ECHO 是矩形， ∴OE=CH= ，BH=BC﹣CH= ， 在 Rt△OBH 中，OH= =2， ∴EC=OH=2，BE= =2 ， ∵∠EBC=∠EBD，∠BED=∠C=90°， ∴△BCE∽△BED， ∴ = ， ∴ = ， ∴DE= ． 25．（2018•北京）下面是小东设计的“过直线外一点作这条直线的平行线”的尺 规作图过程． 已知：直线 l 及直线 l 外一点 P． 求作：直线 PQ，使得 PQ∥l． 作法：如图， ①在直线 l 上取一点 A，作射线 PA，以点 A 为圆心，AP 长为半径画弧，交 PA 的 延长线于点 B； ②在直线 l 上取一点 C（不与点 A 重合），作射线 BC，以点 C 为圆心，CB 长为 半径画弧，交 BC 的延长线于点 Q； ③作直线 PQ．所以直线 PQ 就是所求作的直线． 根据小东设计的尺规作图过程， （1）使用直尺和圆规，补全图形；（保留作图痕迹） （2）完成下面的证明． 证明：∵AB= AP ，CB= CQ ， ∴PQ∥l（ 三角形中位线定理 ）（填推理的依据）． 【分析】（1）根据题目要求作出图形即可； （2）利用三角形中位线定理证明即可； 【解答】（1）解：直线 PQ 如图所示； （2）证明：∵AB=AP，CB=CQ， ∴PQ∥l（三角形中位线定理）． 故答案为：AP，CQ，三角形中位线定理； 26．（2018•白银）如图，在△ABC 中，∠ABC=90°． （1）作∠ACB 的平分线交 AB 边于点 O，再以点 O 为圆心，OB 的长为半径作⊙ O；（要求：不写做法，保留作图痕迹） （2）判断（1）中 AC 与⊙O 的位置关系，直接写出结果． 【分析】（1）首先利用角平分线的作法得出 CO，进而以点 O 为圆心，OB 为半 径作⊙O 即可； （2）利用角平分线的性质以及直线与圆的位置关系进而求出即可． 【解答】解：（1）如图所示： ； （2）相切；过 O 点作 OD⊥AC 于 D 点， ∵CO 平分∠ACB， ∴OB=OD，即 d=r， ∴⊙O 与直线 AC 相切， 27．（2018•无锡）如图，平面直角坐标系中，已知点 B 的坐标为（6，4）． （1）请用直尺（不带刻度）和圆规作一条直线 AC，它与 x 轴和 y 轴的正半轴分 别交于点 A 和点 C，且使∠ABC=90°，△ABC 与△AOC 的面积相等．（作图不必 写作法，但要保留作图痕迹．） （2）问：（1）中这样的直线 AC 是否唯一？若唯一，请说明理由；若不唯一， 请在图中画出所有这样的直线 AC，并写出与之对应的函数表达式． 【分析】（1）①作线段 OB 的垂直平分线 AC，满足条件，②作矩形 OA′BC′，直 线 A′C′，满足条件； （2）分两种情形分别求解即可解决问题； 【解答】（1）解：如图△ABC 即为所求； （2）解：这样的直线不唯一． ①作线段 OB 的垂直平分线 AC，满足条件，此时直线的解析式为 y=﹣ x+ ． ②作矩形 OA′BC′，直线 A′C′，满足条件，此时直线 A′C′的解析式为 y=﹣ x+4． 28．（2018•孝感）如图，△ABC 中，AB=AC，小聪同学利用直尺和圆规完成了 如下操作： ①作∠BAC 的平分线 AM 交 BC 于点 D； ②作边 AB 的垂直平分线 EF，EF 与 AM 相交于点 P； ③连接 PB，PC． 请你观察图形解答下列问题： （1）线段 PA，PB，PC 之间的数量关系是 PA=PB=PC ； （2）若∠ABC=70°，求∠BPC 的度数． 【分析】（1）根据线段的垂直平分线的性质可得：PA=PB=PC； （2）根据等腰三角形的性质得：∠ABC=∠ACB=70°，由三角形的内角和得：∠ BAC=180°﹣2×70°=40°，由角平分线定义得：∠BAD=∠CAD=20°，最后利用三角 形外角的性质可得结论． 【解答】解：（1）如图，PA=PB=PC，理由是： ∵AB=AC，AM 平分∠BAC， ∴AD 是 BC 的垂直平分线， ∴PB=PC， ∵EP 是 AB 的垂直平分线， ∴PA=PB， ∴PA=PB=PC； 故答案为：PA=PB=PC； （2）∵AB=AC， ∴∠ABC=∠ACB=70°， ∴∠BAC=180°﹣2×70°=40°， ∵AM 平分∠BAC， ∴∠BAD=∠CAD=20°， ∵PA=PB=PC， ∴∠ABP=∠BAP=∠ACP=20°， ∴∠BPC=∠ABP+∠BAC+∠ACP=20°+40°+20°=80°． 29．（2018•深圳）已知菱形的一个角与三角形的一个角重合，然后它的对角顶 点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在△CFE 中，CF=6，CE=12，∠FCE=45°，以点 C 为圆心，以任意长为半径作 AD，再分别 以点 A 和点 D 为圆心，大于 AD 长为半径作弧，交 EF 于点 B，AB∥CD． （1）求证：四边形 ACDB 为△FEC 的亲密菱形； （2）求四边形 ACDB 的面积． 【分析】（1）根据折叠和已知得出 AC=CD，AB=DB，∠ACB=∠DCB，求出 AC=AB， 根据菱形的判定得出即可； （2）根据相似三角形的性质得出比例式，求出菱形的边长和高，根据菱形的面 积公式求出即可． 【解答】（1）证明：∵由已知得：AC=CD，AB=DB， 由已知尺规作图痕迹得：BC 是∠FCE 的角平分线， ∴∠ACB=∠DCB， 又∵AB∥CD， ∴∠ABC=∠DCB， ∴∠ACB=∠ABC， ∴AC=AB， 又∵AC=CD，AB=DB， ∴AC=CD=DB=BA∴四边形 ACDB 是菱形， ∵∠ACD 与△FCE 中的∠FCE 重合，它的对角∠ABD 顶点在 EF 上， ∴四边形 ACDB 为△FEC 的亲密菱形； （2）解：设菱形 ACDB 的边长为 x， ∵四边形 ABCD 是菱形， ∴AB∥CE， ∴∠FAB=∠FCE，∠FBA=∠E， △EAB∽△FCE 则： ， 即 ， 解得：x=4， 过 A 点作 AH⊥CD 于 H 点， ∵在 Rt△ACH 中，∠ACH=45°， ∴ ， ∴四边形 ACDB 的面积为： ． 30．（2018•贵港）尺规作图（只保留作图痕迹，不要求写出作法）．如图，已 知∠α和线段 a，求作△ABC，使∠A=∠α，∠C=90°，AB=a． 【分析】根据作一个角等于已知角，线段截取以及垂线的尺规作法即可求出答案． 【解答】解：如图所示， △ABC 为所求作 31．（2018•江西）如图，在四边形 ABCD 中，AB∥CD，AB=2CD，E 为 AB 的中 点，请仅用无刻度直尺分别按下列要求画图（保留画图痕迹）． （1）在图 1 中，画出△ABD 的 BD 边上的中线； （2）在图 2 中，若 BA=BD，画出△ABD 的 AD 边上的高． 【分析】（1）连接 EC，利用平行四边形的判定和性质解答即可； （2）连接 EC，ED，FA，利用三角形重心的性质解答即可． 【 解 答 】 解 ： （ 1 ） 如 图 1 所 示 ， AF 即 为 所 求 ： （2）如图 2 所示，BH 即为所求． 32．（2018•青岛）已知：如图，∠ABC，射线 BC 上一点 D． 求作：等腰△PBD，使线段 BD 为等腰△PBD 的底边，点 P 在∠ABC 内部，且点 P 到∠ABC 两边的距离相等． 【分析】根据角平分线的性质、线段的垂直平分线的性质即可解决问题． 【解答】解：∵点 P 在∠ABC 的平分线上， ∴点 P 到∠ABC 两边的距离相等（角平分线上的点到角的两边距离相等）， ∵点 P 在线段 BD 的垂直平分线上， ∴PB=PD（线段的垂直平分线上的点到线段的两个端点的距离相等）， 如图所示： 33．（2018•宁波）在 5×3 的方格纸中，△ABC 的三个顶点都在格点上． （1）在图 1 中画出线段 BD，使 BD∥AC，其中 D 是格点； （2）在图 2 中画出线段 BE，使 BE⊥AC，其中 E 是格点． 【分析】（1）将线段 AC 沿着 AB 方向平移 2 个单位，即可得到线段 BD； （2）利用 2×3 的长方形的对角线，即可得到线段 BE⊥AC． 【解答】解：（1）如图所示，线段 BD 即为所求； （2）如图所示，线段 BE 即为所求． 34．（2018•河南）如图，反比例函数 y= （x＞0）的图象过格点（网格线的交 点）P． （1）求反比例函数的解析式； （2）在图中用直尺和 2B 铅笔画出两个矩形（不写画法），要求每个矩形均需满 足下列两个条件： ①四个顶点均在格点上，且其中两个顶点分别是点 O，点 P； ②矩形的面积等于 k 的值． 【分析】（1）将 P 点坐标代入 y= ，利用待定系数法即可求出反比例函数的解 析式； （2）根据矩形满足的两个条件画出符合要求的两个矩形即可． 【解答】解：（1）∵反比例函数 y= （x＞0）的图象过格点 P（2，2）， ∴k=2×2=4， ∴反比例函数的解析式为 y= ； （2）如图所示： 矩形 OAPB、矩形 OCDP 即为所求作的图形． 35．（2018•金华）如图，在 6×6 的网格中，每个小正方形的边长为 1，点 A 在 格点（小正方形的顶点）上．试在各网格中画出顶点在格点上，面积为 6，且符 合相应条件的图形． 【分析】利用数形结合的思想解决问题即可； 【解答】解：符合条件的图形如图所示： 36．（2018•济宁）在一次数学活动课中，某数学小组探究求环形花坛（如图所 示）面积的方法，现有以下工具；①卷尺；②直棒 EF；③T 型尺（CD 所在的直 线垂直平分线段 AB）． （1）在图 1 中，请你画出用 T 形尺找大圆圆心的示意图（保留画图痕迹，不写 画法）； （2）如图 2，小华说：“我只用一根直棒和一个卷尺就可以求出环形花坛的面积， 具体做法如下： 将直棒放置到与小圆相切，用卷尺量出此时直棒与大圆两交点 M，N 之间的距离， 就可求出环形花坛的面积”如果测得 MN=10m，请你求出这个环形花坛的面积． 【分析】（1）直线 CD 与 C′D′的交点即为所求的点 O． （2）设切点为 C，连接 OM，OC．旅游勾股定理即可解决问题； 【解答】解：（1）如图点 O 即为所求； （2）设切点为 C，连接 OM，OC． ∵MN 是切线， ∴OC⊥MN， ∴CM=CN=5， ∴OM2﹣OC2=CM2=25， ∴S 圆环=π•OM2﹣π•OC2=25π． 37．（2018•广安）下面有 4 张形状、大小完全相同的方格纸，方格纸中的每个 小正方形的边长都是 1，请在方格纸中分别画出符合要求的图形，所画图形各顶 点必须与方格纸中小正方形的顶点重合，具体要求如下： （1）画一个直角边长为 4，面积为 6 的直角三角形． （2）画一个底边长为 4，面积为 8 的等腰三角形． （3）画一个面积为 5 的等腰直角三角形． （4）画一个边长为 2 ，面积为 6 的等腰三角形． 【分析】（1）利用三角形面积求法以及直角三角形的性质画即可； （2）利用三角形面积求法以及等腰三角形的性质画出即可． （3）利用三角形面积求法以及等腰直角三角形的性质画出即可； （4）利用三角形面积求法以及等腰三角形的性质画出即可． 【 解 答 】 解 ： （ 1 ） 如 图 （ 1 ） 所 示 ： （2）如图（2）所示： （3）如图（3）所示； （4）如图（4）所示． 38．（2018•青岛）问题提出：用若干相同的一个单位长度的细直木棒，按照如 图 1 方式搭建一个长方体框架，探究所用木棒条数的规律． 问题探究： 我们先从简单的问题开始探究，从中找出解决问题的方法． 探究一 用若干木棒来搭建横长是 m，纵长是 n 的矩形框架（m、n 是正整数），需要木 棒的条数． 如图①，当 m=1，n=1 时，横放木棒为 1×（1+1）条，纵放木棒为（1+1）×1 条，共需 4 条； 如图②，当 m=2，n=1 时，横放木棒为 2×（1+1）条，纵放木棒为（2+1）×1 条，共需 7 条； 如图③，当 m=2，n=2 时，横放木棒为 2×（2+1））条，纵放木棒为（2+1）× 2 条，共需 12 条；如图④，当 m=3，n=1 时，横放木棒为 3×（1+1）条，纵放 木棒为（3+1）×1 条，共需 10 条； 如图⑤，当 m=3，n=2 时，横放木棒为 3×（2+1）条，纵放木棒为（3+1）×2 条，共需 17 条． 问题（一）：当 m=4，n=2 时，共需木棒 22 条． 问题（二）：当矩形框架横长是 m，纵长是 n 时，横放的木棒为 m（n+1） 条， 纵放的木棒为 n（m+1） 条． 探究二 用若干木棒来搭建横长是 m，纵长是 n，高是 s 的长方体框架（m、n、s 是正整 数），需要木棒的条数． 如图⑥，当 m=3，n=2，s=1 时，横放与纵放木棒之和为[3×（2+1）+（3+1）× 2]×（1+1）=34 条，竖放木棒为（3+1）×（2+1）×1=12 条，共需 46 条； 如图⑦，当 m=3，n=2，s=2 时，横放与纵放木棒之和为[3×（2+1）+（3+1）× 2]×（2+1）=51 条，竖放木棒为（3+1）×（2+1）×2=24 条，共需 75 条； 如图⑧，当 m=3，n=2，s=3 时，横放与纵放木棒之和为[3×（2+1）+（3+1）× 2]×（3+1）=68 条，竖放木棒为（3+1）×（2+1）×3=36 条，共需 104 条． 问题（三）：当长方体框架的横长是 m，纵长是 n，高是 s 时，横放与纵放木棒 条数之和为 [m（n+1）+n（m+1）]（s+1） 条，竖放木棒条数为 （m+1） （n+1）s 条． 实际应用：现在按探究二的搭建方式搭建一个纵长是 2、高是 4 的长方体框架， 总共使用了 170 条木棒，则这个长方体框架的横长是 4 ． 拓展应用：若按照如图 2 方式搭建一个底面边长是 10，高是 5 的正三棱柱框架， 需要木棒 1320 条． 【分析】从特殊到一般探究规律后利用规律即可解决问题； 【解答】解：问题（一）：当 m=4，n=2 时，横放木棒为 4×（2+1）条，纵放木 棒为（4+1）×2 条，共需 22 条； 问题（二）：当矩形框架横长是 m，纵长是 n 时，横放的木棒为 m（n+1）条， 纵放的木棒为 n（m+1）条； 问题（三）：当长方体框架的横长是 m，纵长是 n，高是 s 时，横放与纵放木棒 条数之和为[m（n+1）+n（m+1）]（s+1）条，竖放木棒条数为（m+1）（n+1） s 条． 实际应用：这个长方体框架的横长是 s，则：[3m+2（m+1）]×5+（m+1）×3 ×4=170，解得 m=4， 拓展应用：若按照如图 2 方式搭建一个底面边长是 10，高是 5 的正三棱柱框架， 横放与纵放木棒条数之和为 165×6=990 条，竖放木棒条数为 66×5=330 条需要 木棒 1320 条． 故答案为 22，m（n+1），n（m+1），[m（n+1）+n（m+1）]（s+1），（m+1） （n+1）s，4，1320； 39．（2018•香坊区）如图，在每个小正方形的边长均为 1 的方格纸中，有线段 AB 和线段 CD，点 A、B、C、D 均在小正方形的顶点上． （1）在方格纸中画出以 AB 为斜边的等腰直角三角形 ABE，点 E 在小正方形的顶 点上； （2）在方格纸中画出以 CD 为对角线的矩形 CMDN（顶点字母按逆时针顺序）， 且面积为 10，点 M、N 均在小正方形的顶点上； （3）连接 ME，并直接写出 EM 的长． 【分析】（1）利用等腰直角三角形的性质画出即可； （2）利用矩形的性质画出即可； （3）根据勾股定理解答即可． 【解答】解：（1）如图所示； （2）如图所示； （3）如图所示，EM= 40．（2018•天门）图①、图②都是由边长为 1 的小菱形构成的网格，每个小菱 形的顶点称为格点．点 O，M，N，A，B 均在格点上，请仅用无刻度直尺在网格 中完成下列画图． （1）在图①中，画出∠MON 的平分线 OP； （2）在图②中，画一个 Rt△ABC，使点 C 在格点上． 【分析】（1）构造全等三角形，利用全等三角形的性质即可解决问题； （2）利用菱形以及平行线的性质即可解决问题； 【解答】解：（1）如图所示，射线 OP 即为所求． （2）如图所示，点 C 即为所求； 41．（2018•哈尔滨）如图，方格纸中每个小正方形的边长均为 1，线段 AB 的两 个端点均在小正方形的顶点上． （1）在图中画出以线段 AB 为一边的矩形 ABCD（不是正方形），且点 C 和点 D 均在小正方形的顶点上； （2）在图中画出以线段 AB 为一腰，底边长为 2 的等腰三角形 ABE，点 E 在小 正方形的顶点上，连接 CE，请直接写出线段 CE 的长． 【分析】（1）利用数形结合的思想解决问题即可； （2）利用数形结合的思想解决问题即可； 【解答】解：（1）如图所示，矩形 ABCD 即为所求； （2）如图△ABE 即为所求，CE=4．