中考数学模拟复习试卷doc1 9页

‎2012年山东省滨州市中考数学试卷 一．选择题：本大题共12个小题，在每个小题的四个选项中只有一个是正确的，请把正确的选出来，并将其字母标号填写在答题栏内．每小题选对得3分，选错、不选或选出的答案超过一个均记0分，满分36分．‎ ‎1．（2012滨州） 等于（　　）‎ ‎　　A． 　　B．6　　C．　　D．8‎ 考点：有理数的乘方。‎ 解答：解：．‎ 故选C．‎ ‎2．（2012滨州）以下问题，不适合用全面调查的是（　　）‎ A．了解全班同学每周体育锻炼的时间　　B．鞋厂检查生产的鞋底能承受的弯折次数　　C．学校招聘教师，对应聘人员面试　　D．黄河三角洲中学调查全校753名学生的身高 考点：全面调查与抽样调查。‎ 解答：解：A、数量不大，应选择全面调查；‎ B、数量较大，具有破坏性的调查，应选择抽样调查；‎ C、事关重大，调查往往选用普查；‎ D、数量较不大应选择全面调查．‎ 故选B．‎ ‎3．（2012滨州）借助一副三角尺，你能画出下面哪个度数的角（　　）‎ ‎　　A．65°　　B．75°　　C．85°　　D．95°‎ 考点：角的计算。‎ 解答：解：利用一副三角板可以画出75°角，用45°和30°的组合即可，‎ 故选：B．‎ ‎4．（2012滨州）一个三角形三个内角的度数之比为2：3：7，这个三角形一定是（　　）‎ ‎　　A．等腰三角形　　B．直角三角形　　C．锐角三角形　　D．钝角三角形 考点：三角形内角和定理。‎ 解答：解：三角形的三个角依次为180°×=30°，180°×=45°，180°×=105°，所以这个三角形是钝角三角形．故选D．‎ ‎5．（2012滨州）不等式的解集是（　　）‎ ‎　　A． 　　B．　　C． 　　D．空集 考点：解一元一次不等式组。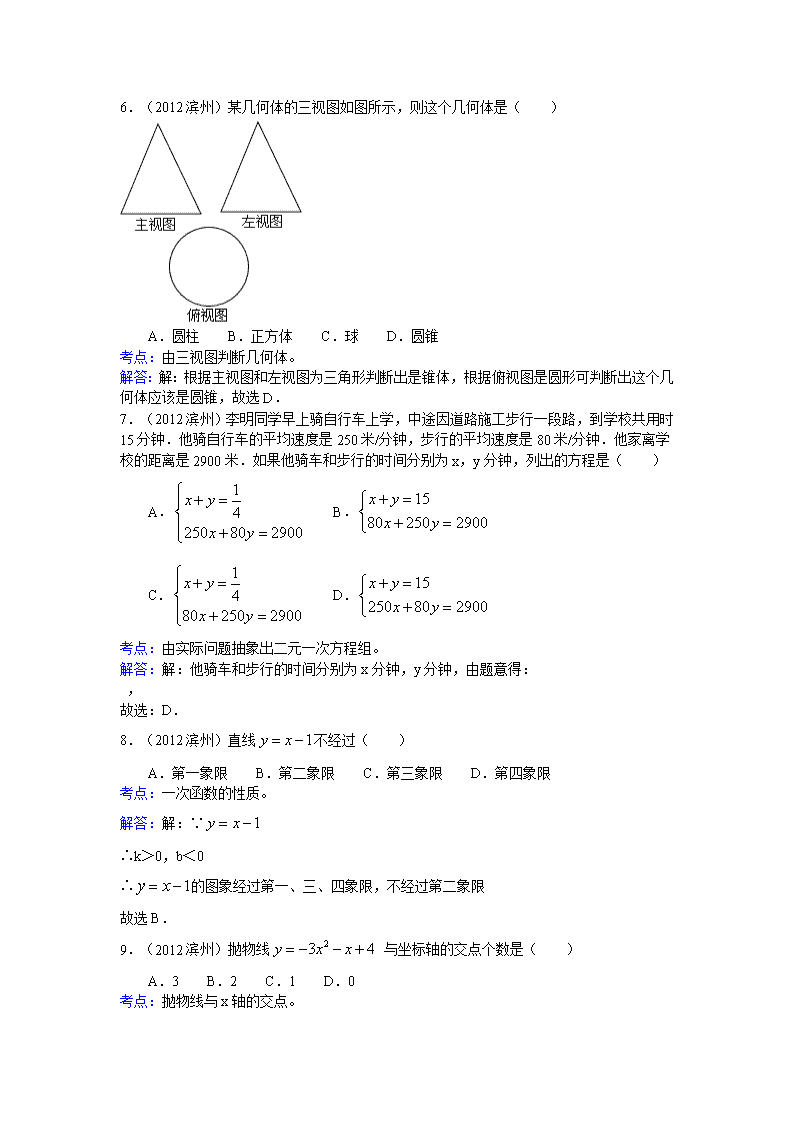‎ 解答：解：，‎ 解①得：，‎ 解②得：．‎ 则不等式组的解集是：．‎ 故选A．‎ ‎6．（2012滨州）某几何体的三视图如图所示，则这个几何体是（　　）‎ ‎　　A．圆柱　　B．正方体　　C．球　　D．圆锥 考点：由三视图判断几何体。‎ 解答：解：根据主视图和左视图为三角形判断出是锥体，根据俯视图是圆形可判断出这个几何体应该是圆锥，故选D．‎ ‎7．（2012滨州）李明同学早上骑自行车上学，中途因道路施工步行一段路，到学校共用时15分钟．他骑自行车的平均速度是250米/分钟，步行的平均速度是80米/分钟．他家离学校的距离是2900米．如果他骑车和步行的时间分别为x，y分钟，列出的方程是（　　）‎ A．　　B．　‎ C．　　D．‎ 考点：由实际问题抽象出二元一次方程组。‎ 解答：解：他骑车和步行的时间分别为x分钟，y分钟，由题意得：‎ ‎ ，‎ 故选：D．‎ ‎8．（2012滨州）直线不经过（　　）‎ ‎　　A．第一象限　　B．第二象限　　C．第三象限　　D．第四象限 考点：一次函数的性质。‎ 解答：解：∵‎ ‎∴k＞0，b＜0‎ ‎∴的图象经过第一、三、四象限，不经过第二象限 故选B．‎ ‎9．（2012滨州）抛物线 与坐标轴的交点个数是（　　）‎ ‎　　A．3　　B．2　　C．1　　D．0‎ 考点：抛物线与x轴的交点。‎ 解答：解：抛物线解析式，‎ 令x=0，解得：y=4，∴抛物线与y轴的交点为（0，4），‎ 令y=0，得到，即，‎ 分解因式得： ，‎ 解得： , ，‎ ‎∴抛物线与x轴的交点分别为（，0），（1，0），‎ 综上，抛物线与坐标轴的交点个数为3．‎ 故选A ‎10．（2012滨州）把△ABC三边的长度都扩大为原来的3倍，则锐角A的正弦函数值（　　）‎ ‎　　A．不变　　B．缩小为原来的　　C．扩大为原来的3倍　　D．不能确定 考点：锐角三角函数的定义。‎ 解答：解：因为△ABC三边的长度都扩大为原来的3倍所得的三角形与原三角形相似，所以锐角A的大小没改变，所以锐角A的正弦函数值也不变．‎ 故选A．‎ ‎11．（2012滨州）菱形的周长为8cm，高为1cm，则该菱形两邻角度数比为（　　）‎ ‎　　A．3：1　　B．4：1　　C．5：1　　D．6：1‎ 考点：菱形的性质；含30度角的直角三角形。‎ 解答：解：如图所示，根据已知可得到菱形的边长为2cm，从而可得到高所对的角为30°，相邻的角为150°，则该菱形两邻角度数比为5：1．‎ 故选C．‎ ‎ ‎ ‎12．（2012滨州）求1+2+22+23+…+22012的值，可令S=1+2+22+23+…+22012，则2S=2+22+23+24+…+22013，因此2S﹣S=22013﹣1．仿照以上推理，计算出1+5+52+53+…+52012的值为（　　）‎ ‎　　A．52012﹣1　　B．52013﹣1　　C．　　D．‎ 考点：同底数幂的乘法。‎ 解答：解：设S=1+5+52+53+…+52012，则5S=5+52+53+54+…+52013，‎ 因此，5S﹣S=52013﹣1，‎ S=．‎ 故选C．‎ 二．填空题：本大题共6个小题，每小题填对最后结果得4分，满分24分．14,17,18题错填不得分，只填一个正确答案得2分。‎ ‎13．（2012滨州）如表是晨光中学男子篮球队队员的年龄统计：‎ ‎ 年龄 ‎13 ‎ ‎14 ‎ ‎ 15‎ ‎ 16‎ ‎ 人数 ‎ 1‎ ‎ 5‎ ‎ 5‎ ‎ 1‎ 他们的平均年龄是 ．‎ 考点：加权平均数。‎ 解答：解：他们的平均年龄是：（13×1+14×5+15×5+16×1）÷12=14.5（岁）；‎ 故答案为：14.5．‎ ‎14．（2012滨州）下列函数：①y=2x﹣1；②y=﹣；③y=x2+8x﹣2；④y=；⑤y=；⑥y=中，y是x的反比例函数的有 （填序号）‎ 考点：反比例函数的定义。‎ 解答：解：①y=2x﹣1是一次函数，不是反比例函数；‎ ‎②y=是反比例函数；‎ ‎③y=x2+8x﹣2是二次函数，不是反比例函数；‎ ‎④y=不是反比例函数；‎ ‎⑤y=是反比例函数；‎ ‎⑥y=中，a≠0时，是反比例函数，没有此条件则不是反比例函数；‎ 故答案为：②⑤．‎ ‎15．（2012滨州）根据你学习的数学知识，写出一个运算结果为a6的算式 ．‎ 考点：幂的乘方与积的乘方；同底数幂的乘法；同底数幂的除法。‎ 解答：解：a4a2=a6．‎ 故答案是a4a2=a6（答案不唯一）．‎ ‎16．（2012滨州）如图，在△ABC中，AB=AD=DC，∠BAD=20°，则∠C= ．‎ 考点：三角形的外角性质；三角形内角和定理。‎ 解答：解：∵AB=AD，∠BAD=20°，‎ ‎∴∠B===80°，‎ ‎∵∠ADC是△ABD的外角，‎ ‎∴∠ADC=∠B+∠BAD=80°+20°=100°，‎ ‎∵AD=DC，‎ ‎∴∠C===40°．‎ ‎17．（2012滨州）方程x（x﹣2）=x的根是 ．‎ 考点：解一元二次方程-因式分解法。‎ 解答：解：原方程可化为x（x﹣2）﹣x=0，‎ x（x﹣2﹣1）=0，‎ x=0或x﹣3=0，‎ 解得：x1=0，x2=3．‎ ‎18．（2012滨州）如图，锐角三角形ABC的边AB，AC上的高线CE和BF相交于点D，请写出图中的两对相似三角形： （用相似符号连接）．‎ 考点：相似三角形的判定。‎ 解答：解：（1）在△BDE和△CDF中 ‎∠BDE=∠CDF∠BED=∠CFD=90°‎ ‎∴△BDE∽△CDF ‎（2）在△ABF和△ACE中 ‎∵∠A=∠A，∠AFB=∠AEC=90°‎ ‎∴△ABF∽△ACE 三．解答题：本大题共7个小题，满分60分．‎ ‎19．（2012滨州）计算： ‎ 考点：实数的运算；零指数幂；负整数指数幂。‎ 解答：解：原式= ‎ ‎20．（2012滨州）滨州市体育局要组织一次篮球赛，赛制为单循环形式（每两队之间都赛一场），计划安排28场比赛，应邀请多少支球队参加比赛？学习以下解答过程，并完成填空．‎ 解：设应邀请x支球队参赛，则每对共打 场比赛，比赛总场数用代数式表示为 ．根据题意，可列出方程 ．‎ 整理，得 ．‎ 解这个方程，得 ．‎ 合乎实际意义的解为 ．‎ 答：应邀请 支球队参赛．‎ 考点：一元二次方程的应用。‎ 解答：解：设应邀请x支球队参赛，则每对共打 （x﹣1）场比赛，比赛总场数用代数式表示为 x（x﹣1）．‎ 根据题意，可列出方程x（x﹣1）=28．‎ 整理，得x2﹣x=28，‎ 解这个方程，得 x1=8，x2=﹣7．‎ 合乎实际意义的解为 x=8．‎ 答：应邀请 8支球队参赛．‎ 故答案为：（x﹣1； x（x﹣1）；x（x﹣1）=28；x2﹣x=28；x1=8，x2=﹣7；x=8；8．‎ ‎21．（2012滨州）如图，PA，PB是⊙O的切线，A，B为切点，AC是⊙O的直径，∠P=50°，求∠BAC的度数．‎ 考点：切线的性质。‎ 解答：解：∵PA，PB分别切⊙O于A，B点，AC是⊙O的直径，‎ ‎∴∠PAC=90°，PA=PB，‎ 又∵∠P=50°，‎ ‎∴∠PAB=∠PBA==65°，‎ ‎∴∠BAC=∠PAC﹣∠PAB=90°﹣65°=25°．‎ ‎22．（2012滨州）在一个口袋中有4个完全相同的小球，把它们分别标上数字﹣1，0，1，2，随机的摸出一个小球记录数字然后放回，在随机的摸出一个小球记录数字．求下列事件的概率：‎ ‎（1）两次都是正数的概率P（A）；‎ ‎（2）两次的数字和等于0的概率P（B）．‎ 考点：列表法与树状图法。‎ 解答：解：（1）画树状图，www.xk b 1.com 所有可能出现的结果共有16种，每种结果出现的可能性都相同，两个数字都是正数的结果有4种，所以P（A）=；‎ ‎（2）如图，‎ 所有可能出现的结果共有16种，每种结果出现的可能性都相同，两个数字和为0的结果有3种，所以P（B）=．‎ ‎23．（2012滨州）我们知道“连接三角形两边中点的线段叫三角形的中位线”，“三角形的中位线平行于三角形的第三边，且等于第三边的一半”．类似的，我们把连接梯形两腰中点的线段叫做梯形的中位线．如图，在梯形ABCD中，AD∥BC，点E，F分别是AB，CD的中点，那么EF就是梯形ABCD的中位线．通过观察、测量，猜想EF和AD、BC有怎样的位置和数量关系？并证明你的结论．‎ 考点：梯形中位线定理；全等三角形的判定与性质；三角形中位线定理。‎ 解答：解：结论为：EF∥AD∥BC，EF=（AD+BC）．理由如下：‎ 连接AF并延长交BC于点G．‎ ‎∵AD∥BC∴∠DAF=∠G，‎ 在△ADF和△GCF中，‎ ‎，‎ ‎∴△ADF≌△GCF，‎ ‎∴AF=FG，AD=CG．‎ 又∵AE=EB，‎ ‎∴，‎ 即EF∥AD∥BC，EF=（AD+BC）．‎ ‎24．（2012滨州）如图，在平面直角坐标系中，抛物线y=ax2+bx+c经过A（﹣2，﹣4），O（0，0），B（2，0）三点．‎ ‎（1）求抛物线y=ax2+bx+c的解析式；‎ ‎（2）若点M是该抛物线对称轴上的一点，求AM+OM的最小值．‎ 考点：二次函数综合题。‎ 解答：解：（1）把A（﹣2，﹣4），O（0，0），B（2，0）三点的坐标代入y=ax2+bx+c中，得新 课标 第一 网 解这个方程组，得a=﹣，b=1，c=0‎ 所以解析式为y=﹣x2+x．‎ ‎（2）由y=﹣x2+x=﹣（x﹣1）2+，可得 抛物线的对称轴为x=1，并且对称轴垂直平分线段OB ‎∴OM=BM ‎∴OM+AM=BM+AM 连接AB交直线x=1于M点，则此时OM+AM最小 过点A作AN⊥x轴于点N，‎ 在Rt△ABN中，AB===4，‎ 因此OM+AM最小值为．‎ ‎25．（2012滨州）如图1，l1，l2，l3，l4是一组平行线，相邻2条平行线间的距离都是1个单位长度，正方形ABCD的4个顶点A，B，C，D都在这些平行线上．过点A作AF⊥l3于点F，交l2于点H，过点C作CE⊥l2于点E，交l3于点G．‎ ‎（1）求证：△ADF≌△CBE；‎ ‎（2）求正方形ABCD的面积；‎ ‎（3）如图2，如果四条平行线不等距，相邻的两条平行线间的距离依次为h1，h2，h3，试用h1，h2，h3表示正方形ABCD的面积S．‎ 考点：全等三角形的判定与性质；平行线之间的距离；正方形的性质。‎ 解答：证明：（1）在Rt△AFD和Rt△CEB中，‎ ‎∵AD=BC，AF=CE，‎ ‎∴Rt△AFD≌Rt△CEB；‎ ‎（2）∵∠ABH+∠CBE=90°，∠ABH+∠BAH=90°，‎ ‎∴∠CBE=∠BAH 又∵AB=BC，∠AHB=∠CEB=90°‎ ‎∴△ABH≌△BCE，‎ 同理可得，△ABH≌△BCE≌△CDG≌△DAF，‎ ‎∴S正方形ABCD=4S△ABH+S正方形HEGF ‎=4××2×1+1×1‎ ‎=5；‎ ‎（3）由（1）知，△AFD≌△CEB，故h1=h3，‎ 由（2）知，△ABH≌△BCE≌△CDG≌△DAF，‎ ‎∴S正方形ABCD=4S△ABH+S正方形HEGF ‎=4×（h1+h2）•h1+h22=2h12+2h1h2+h22．‎