2018中考专题几何题 4页

‎1.‎ ‎2.四边形ABCD是平行四边形，AC、BD交于点O，∠1＝∠2．‎ ‎(1)求证：四边形ABCD是矩形；‎ ‎(2)若∠BOC＝120°，AB＝4cm，求四边形ABCD的面积．‎ ‎3.如图，已知OA⊥OB，OA＝4，OB＝3，以AB为边作矩形ABCD，使AD＝a，过点D作DE垂直OA的延长线交于点E．‎ ‎(1)证明：△OAB∽△EDA；‎ ‎(2)当a为何值时，△OAB≌△EDA？*请说明理由，并求此时点 C到OE的距离．‎ ‎4.如图，在△ABC中，点P是边AC上的一个动点，过点P作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．‎ ‎(1)求证：PE＝PF；‎ ‎(2)*当点P在边AC上运动时，四边形BCFE可能是菱形吗？说明理由；‎ ‎(3)*若在AC边上存在点P，使四边形AECF是正方形，且＝．求此时∠A的大小．‎ ‎5.‎ ‎6.如图，四边形为平行四边形，的角平分线交于点，交的延长线于点.‎ 求证：；‎ 连接BF，若，，，求平行四边形的面积 ‎7.如图所示，将一张直角三角形纸片沿斜边上的中线剪开，得到△ACD，再将△ACD沿方向平移到△的位置。若平移开始后点未到达点时，交于点，交于点，连接。当四边形为菱形时，试探究△的形状，并判断△与△是否全等？请说明理由。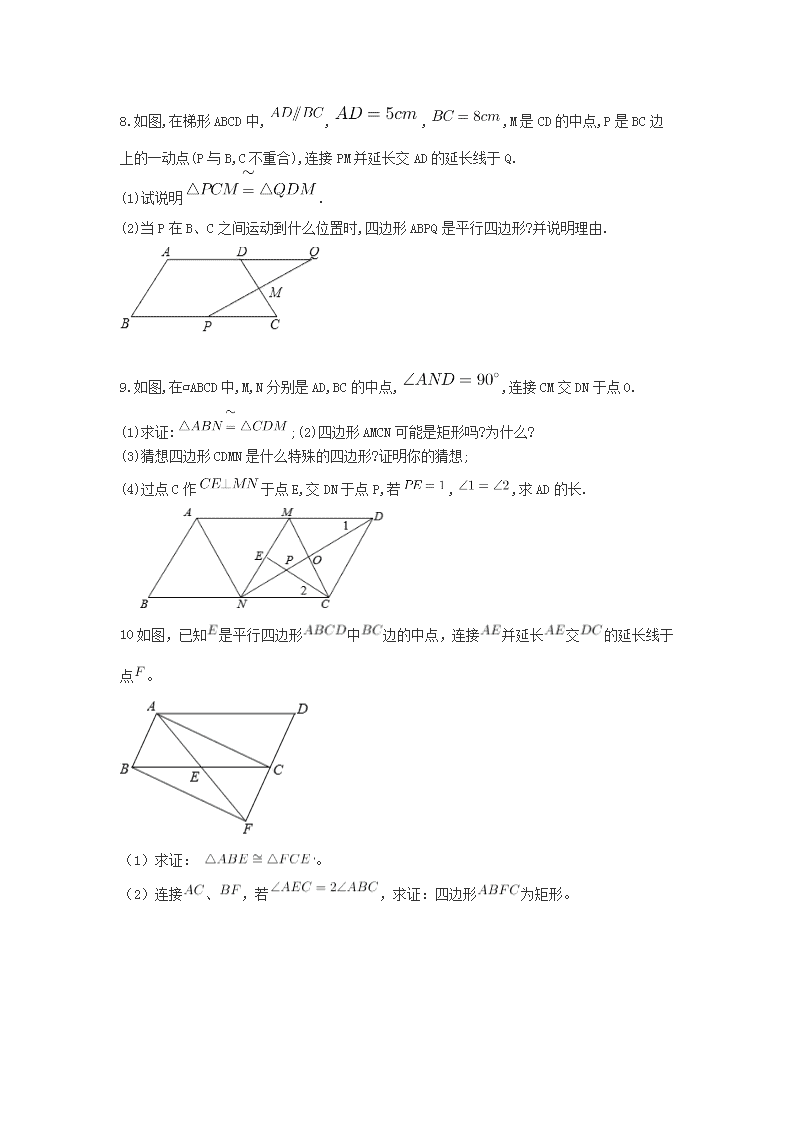‎ ‎8.如图,在梯形ABCD中,,,,M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q. (1)试说明. (2)当P在B、C之间运动到什么位置时,四边形ABPQ是平行四边形?并说明理由.‎ ‎9.如图,在▱ABCD中,M,N分别是AD,BC的中点,,连接CM交DN于点O. (1)求证:;(2)四边形AMCN可能是矩形吗?为什么? (3)猜想四边形CDMN是什么特殊的四边形?证明你的猜想; (4)过点C作于点E,交DN于点P,若,,求AD的长.‎ ‎10如图，已知是平行四边形中边的中点，连接并延长交的延长线于点。‎ ‎（1）求证：。‎ ‎（2）连接、，若，求证：四边形为矩形。‎ ‎11.如图，在矩形中，、分别是、的中点，、分别是、的中点。‎ ‎（1）求证：。‎ ‎（2）四边形是什么样的特殊四边形？请说明理由。‎ ‎12.如图，在矩形中，对角线的垂直平分线与相交于点，与相交于点，连接、。‎ ‎（1）求证：四边形是菱形。‎ ‎（2）若，，求的长。‎