中考数学轨迹问题精选 4页

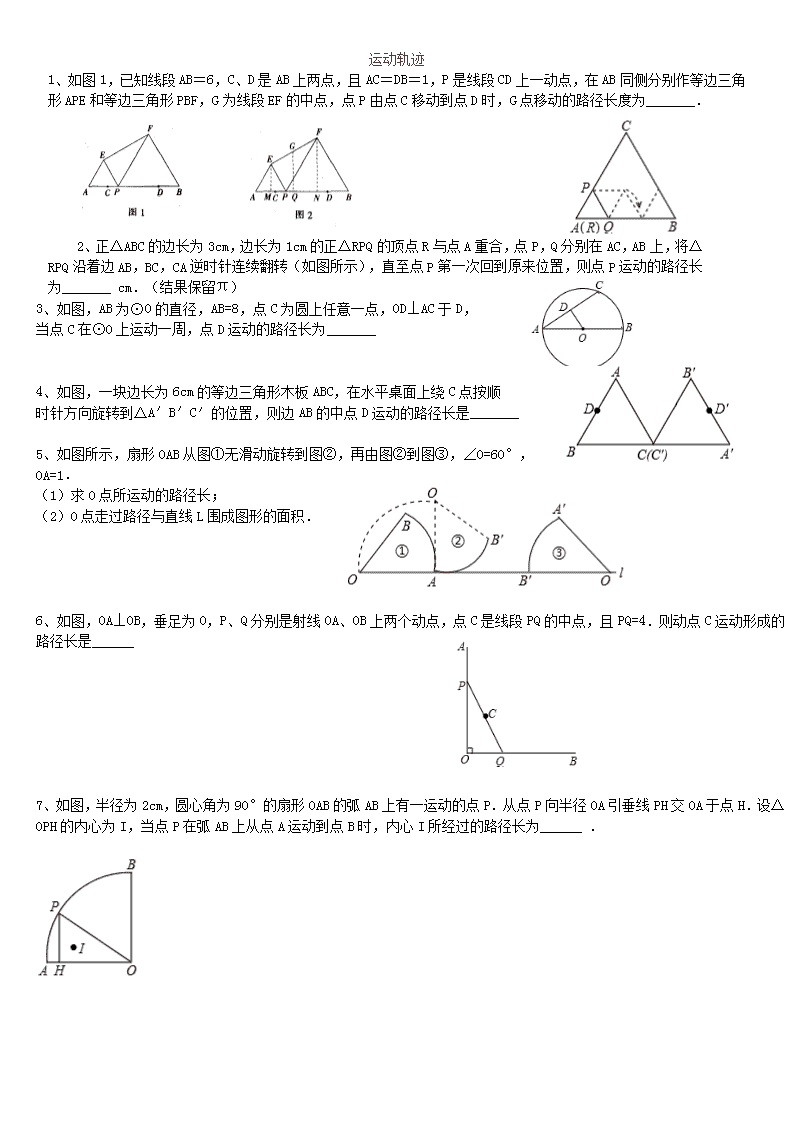
运动轨迹 ‎1、如图1，已知线段AB＝6，C、D是AB上两点，且AC＝DB＝1，P是线段CD上一动点，在AB同侧分别作等边三角形APE和等边三角形PBF，G为线段EF的中点，点P由点C移动到点D时，G点移动的路径长度为_______．‎ ‎ ‎ ‎2、正△ABC的边长为3cm，边长为1cm的正△RPQ的顶点R与点A重合，点P，Q分别在AC，AB上，将△RPQ沿着边AB，BC，CA逆时针连续翻转（如图所示），直至点P第一次回到原来位置，则点P运动的路径长为_______ cm．（结果保留π）‎ ‎3、如图，AB为⊙O的直径，AB=8，点C为圆上任意一点，OD⊥AC于D，‎ 当点C在⊙O上运动一周，点D运动的路径长为_______‎ ‎ ‎ ‎4、如图，一块边长为6cm的等边三角形木板ABC，在水平桌面上绕C点按顺 时针方向旋转到△A′B′C′的位置，则边AB的中点D运动的路径长是_______‎ ‎5、如图所示，扇形OAB从图①无滑动旋转到图②，再由图②到图③，∠O=60°，OA=1． （1）求O点所运动的路径长； （2）O点走过路径与直线L围成图形的面积．‎ ‎6、如图，OA⊥OB，垂足为O，P、Q分别是射线OA、OB上两个动点，点C是线段PQ的中点，且PQ=4．则动点C运动形成的路径长是______‎ ‎7、如图，半径为2cm，圆心角为90°的扇形OAB的弧AB上有一运动的点P．从点P向半径OA引垂线PH交OA于点H．设△OPH的内心为I，当点P在弧AB上从点A运动到点B时，内心I所经过的路径长为______ ．‎ ‎8、某数学兴趣小组对线段上的动点问题进行探究，已知AB=8．‎ 问题思考：‎ 如图1，点P为线段AB上的一个动点，分别以AP、BP为边在同侧作正方形APDC、BPEF．‎ ‎（1）当点P运动时，这两个正方形的面积之和是定值吗？若是，请求出；若不是，请求出这两个正方形面积之和的最小值．‎ ‎（2）分别连接AD、DF、AF，AF交DP于点K，当点P运动时，在△APK、△ADK、△DFK中，是否存在两个面积始终相等的三角形？请说明理由．‎ 问题拓展：‎ ‎（3）如图2，以AB为边作正方形ABCD，动点P、Q在正方形ABCD的边上运动，且PQ=8．若点P从点A出发，沿A→B→C→D的线路，向点D运动，求点P从A到D的运动过程中，PQ的中点O所经过的路径的长．‎ ‎（4）如图3，在“问题思考”中，若点M、N是线段AB上的两点，且AM=BN=1，点G、H分别是边CD、EF的中点，请直接写出点P从M到N的运动过程中，GH的中点O所经过的路径的长及OM+OB的最小值．‎ ‎9、如图，抛物线y=ax2+bx+3过点A（1，0），B（3，0），与y轴相交于点C． （1）求抛物线的解析式； （2）若点E为抛物线对称轴上的一点，请探索抛物线上是否存在点F，使以A，B，E，F为顶点的四边形为平行四边形？若存在，请求出所有点F的坐标；若不存在，请说明理由； （3）若点P为线段OC上的动点，连接BP，过点C作CN垂直于直线BP，垂足为N，当点P从点O运动到点C时，求点N运动路径的长．‎ ‎10、等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连结AF，BE相交于点P.‎ ‎（1）若AE=CF.①求证：AF=BE，并求∠APB的度数.②若AE=2，试求的值.‎ ‎（2）若AF=BE，当点E从点A运动到点C时，试求点P经过的路径长.‎ ‎11、如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动，以CE为直径作⊙O，点F为⊙O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与⊙O相交于点G，连接CG．‎ （1） 试说明四边形EFCG是矩形；‎ （2） 当⊙O与射线BD相切时，点E停止移动．在点E移动的过程中，‎ ① 矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；‎ ② ‎ 求点G移动路线的长．‎