中考中的费马点详解加练习 10页

皮耶·德·费马（Pierre de Fermat）是一个17世纪的法国律师，也是一位业余数学家。‎ 之所以称业余，是由于皮耶·德·费马具有律师的全职工作。他的姓氏根据法文与英文实际发音也常译为“费尔玛”（注意“玛”字）。‎ 费马最后定理在中国习惯称为费马大定理，西方数学界原名“最后”的意思是：其它猜想都证实了，这是最后一个。‎ 著名的数学史学家贝尔（E. T. Bell）在20世纪初所撰写的著作中，称皮耶·德·费马为”业余数学家之王。‎ ‎“贝尔深信，费马比皮耶·德·费马同时代的大多数专业数学家更有成就，然而皮耶·德·费马并未在其他方面另有成就，本人也渐渐退出人们的视野，考虑到17世纪是杰出数学家活跃的世纪，因而贝尔认为费马是17世纪数学家中最多产的明星。‎ 费马点问题最早是由法国数学家皮埃尔·德·费马在一封写给意大利数学家埃万杰利斯塔·托里拆利（气压计的发明者）的信中提出的。‎ 托里拆利最早解决了这个问题，而19世纪的数学家斯坦纳重新发现了这个问题，并系统地进行了推广，因此这个点也称为托里拆利点或斯坦纳点，相关的问题也被称作费马-托里拆利-斯坦纳问题。‎ 这一问题的解决极大推动了联合数学的发展，在近代数学史上具有里程碑式的意义。‎ ‎“费马点”是指位于三角形内且到三角形三个顶点距离之和最短的点。‎ 若给定一个三角形△ABC的话，从这个三角形的费马点P到三角形的三个顶点A、B、C的距离之和比从其它点算起的都要小。‎ 这个特殊点对于每个给定的三角形都只有一个。‎ 1. 若三角形3个内角均小于120°，那么3条距离连线正好三等分费马点所在的周角，即该点所对三角形三边的张角相等，均为120°。‎ 所以三角形的费马点也称为三角形的等角中心。‎ 2. 若三角形有一内角大于等于120°，则此钝角的顶点就是距离和最小的点。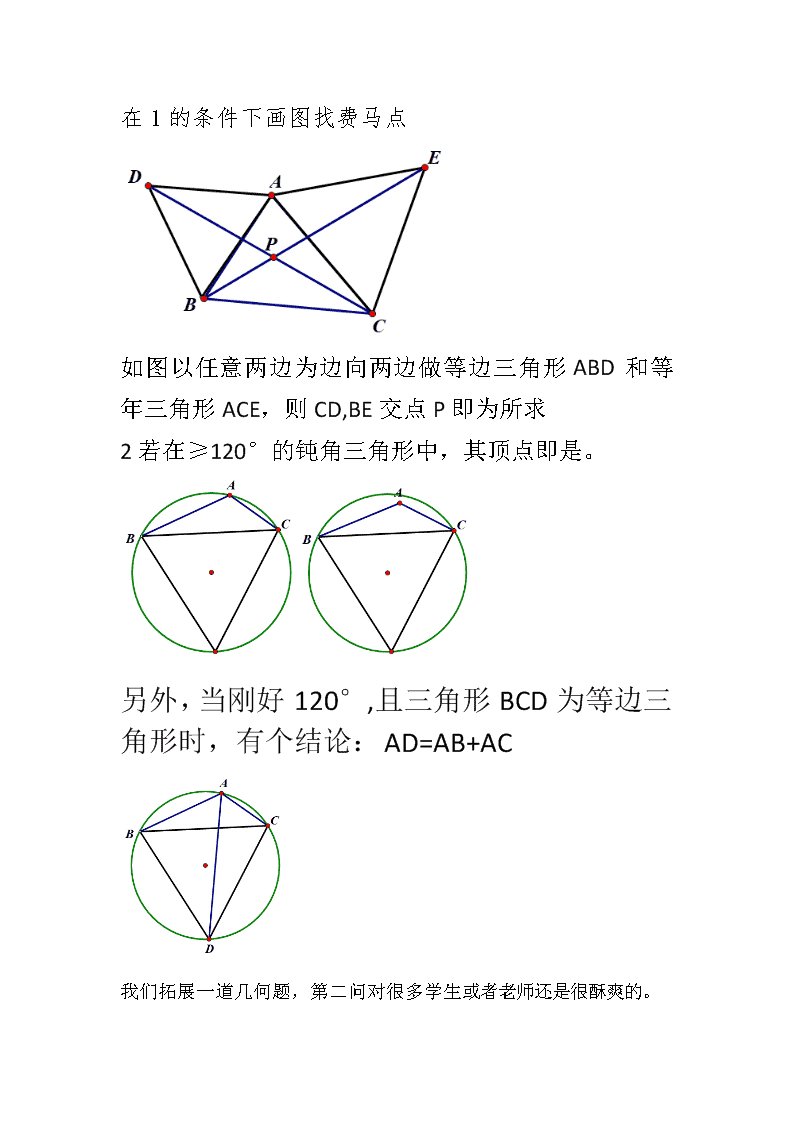‎ 在1的条件下画图找费马点 如图以任意两边为边向两边做等边三角形ABD和等年三角形ACE，则CD,BE交点P即为所求 ‎2若在≥120°的钝角三角形中，其顶点即是。‎ 另外，当刚好120°,且三角形BCD为等边三角形时，有个结论：AD=AB+AC 我们拓展一道几何题，第二问对很多学生或者老师还是很酥爽的。‎ 图1‎ ‎2011房山一摸2009石景山 ‎25．（本小题满分7分）‎ 已知：等边三角形ABC 如图1，P为等边△ABC外一点，且∠BPC=120°．‎ 试猜想线段BP、PC、AP之间的数量关系,并证明你的猜想；‎ 图2‎ ‎（2）如图2，P为等边△ABC内一点，且∠APD=120°．‎ ‎ 求证：PA+PD+PC＞BD ‎ ‎ 我们回到正题：费马点 ‎25.如图，在平面直角坐标系中，点的坐标为，点在轴的正半轴上，，为△的中线，过、两点的抛物线与轴相交于、两点（在的左侧）.‎ ‎（1）求抛物线的解析式；‎ ‎（2）等边△的顶点、在线段上，求及的长；‎ ‎（3）点为△内的一个动点，设，请直接写出的最小值,以及取得最小值时，线段的长.‎ ‎ ‎ ‎2013房山一摸 ‎24．（1）如图1，△ABC和△CDE都是等边三角形，且B、C、D三点共线，联结AD、BE相交于点P，求证：BE=AD．‎ ‎（2）如图2，在△BCD中，∠BCD＜120°，分别以BC、CD和BD为边在△BCD外部作等边三角形ABC、等边三角形CDE和等边三角形BDF，联结AD、BE和CF交于点P，下列结论中正确的是　 　（只填序号即可）‎ ‎①AD=BE=CF；②∠BEC=∠ADC；③∠DPE=∠EPC=∠CPA=60°；‎ ‎（3）如图2，在（2）的条件下，求证：PB+PC+PD=BE．‎ ‎29. 阅读下面材料:‎ 小伟遇到这样一个问题：如图1，在△ABC（其中∠BAC是一个可以变化的角）中，AB=2，AC=4，以BC为边在BC的下方作等边△PBC，求AP的最大值。‎ ‎ 小伟是这样思考的：利用变换和等边三角形将边的位置重新组合．他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A’BC,连接A’A,当点A落在A’C上时,此题可解（如图2）．‎ ‎(1)请你回答：AP的最大值是 ．‎ ‎(2)参考小伟同学思考问题的方法，解决下列问题：‎ ‎ 如图3，等腰Rt△ABC．边AB=4,P为△ABC内部一点，请写出求AP+BP+CP的最小值长的解题思路. ‎ 提示:要解决AP+BP+CP的最小值问题，可仿照题目给出的做法.把⊿ABP绕B点逆时针旋转60，得到.‎ ① 请画出旋转后的图形 ② 请写出求AP+BP+CP的最小值的解题思路（结果可以不化简）.‎ ‎2016一月昌平 ‎28. 已知，点O是等边△ABC内的任一点，连接OA，OB，OC.‎ ‎（1） 如图1，已知∠AOB=150°，∠BOC=120°，将△BOC绕点C按顺时针方向旋转60°得△ADC. ‎ ‎①∠DAO的度数是 ；‎ ‎②用等式表示线段OA，OB，OC之间的数量关系，并证明；‎ ‎（2） 设∠AOB=α，∠BOC=β.‎ ‎①当α，β满足什么关系时，OA+OB+OC有最小值？请在图2中画出符合条件的图形，并说明理由；‎ ‎②若等边△ABC的边长为1，直接写出OA+OB+OC的最小值.‎ ‎2017年一月昌平 ‎29．如图1，在△ABC中，∠ACB=90°，点P为△ABC内一点．‎ ‎（1）连接PB，PC，将△BCP沿射线CA方向平移，得到△DAE，点B，C，P的对应点 分别为点D，A，E，连接CE．‎ ① 依题意，请在图2中补全图形；‎ ② 如果BP⊥CE，BP=3，AB=6，求CE的长．‎ ‎（2）如图3，连接PA，PB，PC，求PA+PB+PC的最小值．‎ 小慧的作法是：以点A为旋转中心，将△ABP顺时针旋转60°得到△AMN，那么就将PA+PB+PC的值转化为CP+PM+MN的值，连接CN，当点P落在CN上时，此题可解．‎ 请你参考小慧的思路，在图3中证明PA+PB+PC=CP+PM+MN．‎ 并直接写出当AC=BC=4时，PA+PB+PC的最小值．‎ 延伸一下 ‎2017年一月 海淀28．在△ABC中，AB=AC，∠BAC=α，点P是△ABC内一点，且．连接PB，试探究PA，PB，PC满足的等量关系．‎ 图1 图2‎ ‎（1）当α=60°时，将△ABP绕点A逆时针旋转60°得到，连接，如图1所示．由≌可以证得是等边三角形，再由可得∠APC的大小为 度，进而得到是直角三角形，这样可以得到PA，PB，PC满足的等量关系为 ；‎ ‎（2）如图2，当α=120°时，请参考（1）中的方法，探究PA，PB，PC满足的等量关系，并给出证明；‎ ‎（3）PA，PB，PC满足的等量关系为 ．‎ ‎2016年顺义一摸 ‎28．已知：在△ABC中，∠BAC=60°．‎ （1） 如图1，若AB=AC，点P在△ABC内，且∠APC=150°，PA=3，PC=4，把△APC绕着点A顺时针旋转，使点C旋转到点B处，得到△ADB，连接DP ‎ ①依题意补全图1；‎ ‎ ②直接写出PB的长；‎ （2） 如图2，若AB=AC，点P在△ABC外，且PA=3，PB=5，PC=4，求∠APC的度数；‎ （3） 如图3，若AB=2AC，点P在△ABC内，且PA=，PB=5，∠APC=120°，请直接写出PC的长．‎ ‎ ‎ ‎ ‎ ‎ 26、如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．‎ ‎（1）求证：△AMB≌△ENB；‎ ‎（2）①当M点在何处时，AM+CM的值最小；‎ ‎②当M点在何处时，AM+BM+CM的值最小，并说明理由；‎ ‎（3）当AM+BM+CM的最小值为时，求正方形的边长．‎ ‎ ‎ 在矩形ABCD中，点P在矩形内，点Q在BC上，AD=5,AB=3,‎ 求AP+DP+PQ的最小值 ‎ ‎