2017中考数学压轴专题最值问题系列一 19页

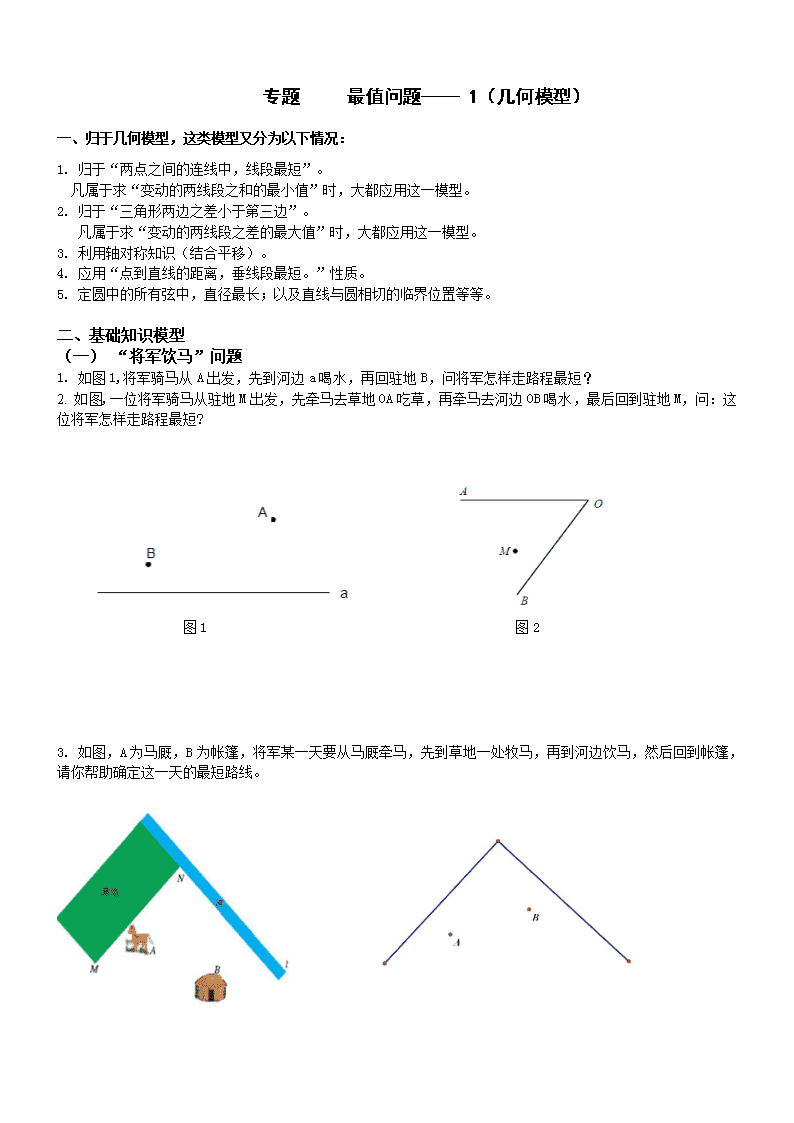
‎ 专题 最值问题—— 1（几何模型）‎ 一、归于几何模型，这类模型又分为以下情况： ‎ ‎1. 归于“两点之间的连线中，线段最短”。‎ ‎ 凡属于求“变动的两线段之和的最小值”时，大都应用这一模型。 ‎ 2. 归于“三角形两边之差小于第三边”。‎ ‎ 凡属于求“变动的两线段之差的最大值”时，大都应用这一模型。 ‎ 3. 利用轴对称知识（结合平移）。‎ ‎4. 应用“点到直线的距离，垂线段最短。”性质。‎ ‎5. 定圆中的所有弦中，直径最长；以及直线与圆相切的临界位置等等。‎ 二、基础知识模型 （一） ‎“将军饮马”问题 1. 如图1,将军骑马从A出发，先到河边a喝水，再回驻地B，问将军怎样走路程最短？‎ 2. 如图,一位将军骑马从驻地M出发，先牵马去草地OA吃草，再牵马去河边OB喝水，最后回到驻地M，问：这位将军怎样走路程最短? ‎ ‎ ‎ ‎ 图1 图2‎ ‎ ‎ ‎3. 如图，A为马厩，B为帐篷，将军某一天要从马厩牵马，先到草地一处牧马，再到河边饮马，然后回到帐篷，请你帮助确定这一天的最短路线。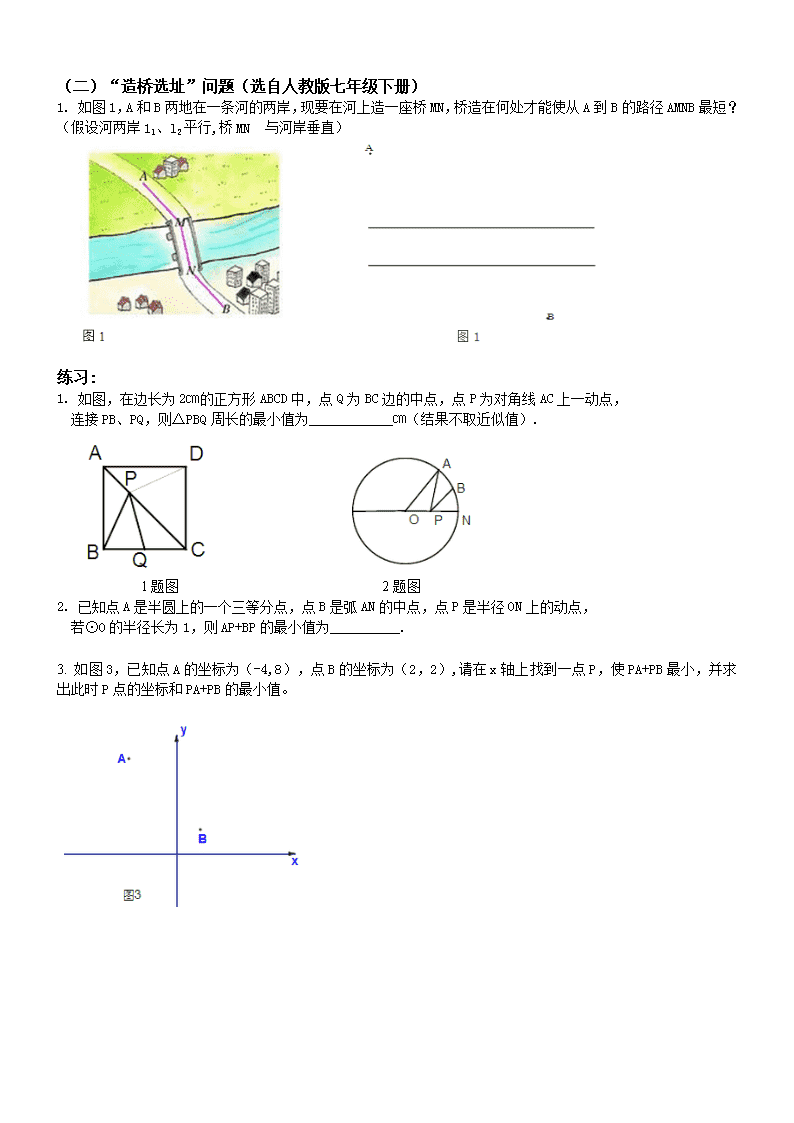‎ ‎ ‎ ‎（二）“造桥选址”问题（选自人教版七年级下册）‎ ‎1. 如图1，A和B两地在一条河的两岸，现要在河上造一座桥MN，桥造在何处才能使从A到B的路径AMNB最短？（假设河两岸1l、l2平行,桥MN 与河岸垂直）‎ ‎ ‎ 练习:‎ ‎1. 如图，在边长为2㎝的正方形ABCD中，点Q为BC边的中点，点P为对角线AC上一动点，‎ ‎ 连接PB、PQ，则△PBQ周长的最小值为____________㎝（结果不取近似值）. ‎ ‎ ‎ ‎ 1题图 2题图 2. 已知点A是半圆上的一个三等分点，点B是弧AN的中点，点P是半径ON上的动点，‎ ‎ 若⊙O的半径长为1，则AP+BP的最小值为__________.‎ ‎ ‎ 3. 如图3，已知点A的坐标为（-4,8），点B的坐标为（2，2）,请在x轴上找到一点P，使PA+PB最小，并求出此时P点的坐标和PA+PB的最小值。‎ ‎ ‎ 变式1: ‎ ‎ 如图，已知点A的坐标为（-4,8），点B的坐标为（2，2）,点C的坐标为（-2，0）.把点A和点B向左平移 ‎ m个单位，得到点和点,使最短，求m的值.‎ ‎ ‎ 变式2: ‎ 如图，已知点A的坐标为（-4,8），点B的坐标为（2，2）,点C的坐标为（-2，0），点D的坐标为（-4，0）.‎ 把点A和点B向左或向右平移m个单位，得到点和点,使四边形CD的周长最短，求m的值.‎ ‎ ‎ ‎ ‎ ‎1.‎ 中考真题练习 ‎ ‎ ‎2.如图（1），抛物线和y轴的交点为A，M为OA的中点，若有一动点P，自M点处出发，沿直线运动到x轴上的某点（设为点E），再沿直线运动到该抛物线对称轴上的某点（设为点F），最后又沿直线运动到点A，求使点P运动的总路程最短的点E，点F的坐标，并求出这个最短路程的长。‎ ‎ ‎ ‎3.‎ ‎ ‎ ‎4.（广州 2014 24题）已知平面直角坐标系中两定点A（﹣1，0）、B（4，0），抛物线y=ax2+bx﹣2（a≠0）过点A，B，顶点为C，点P（m，n）（n＜0）为抛物线上一点． ‎ （1） 求抛物线的解析式和顶点C的坐标； ‎ （2） 当∠APB为钝角时，求m的取值范围； ‎ （3） 若m＞，当∠APB为直角时，将该抛物线向左或向右平移t（0＜t＜）个单位，点C、P平移后对应的点分别记为C′、P′，是否存在t，使得首位依次连接A、B、P′、C′所构成的多边形的周长最短？若存在，求t的值并说明抛物线平移的方向；若不存在，请说明理由．‎ ‎（三）垂线段最短问题 ‎1.如图，点A的坐标为（-1，0），点B在直线上运动，当线段AB最短时，点B的坐标为( )‎ A.（0，0） B.（，） C.（，） D.（，）‎ 变式 ‎1. 已知点A的坐标为（-4，8）,点B的坐标为（2，2）,在y轴上找一点M，使点M到点C（-2，0）的距离和到直线AB的距离之和最小，请求出最小值。‎ ‎  ‎ ‎2. 已知点A的坐标为（-4,8），点B的坐标为（2，2）已知点的坐标为（2，0），在y轴上找一点N，使点N到点的距离和到直线AB的距离之和最小，请求出最小值.‎ ‎ ‎ ‎ ‎ 中考真题训练 ‎1. 如图，已知点A(-4，8)和点B(2，n)在抛物线y=ax2上，点C坐标为（-2，0）. ‎ ‎(1) 求a的值； ‎ ‎(2) 在x轴上找一点Q，使得△QAB的周长最小，求出点Q的坐标；‎ ‎(3) 已知点D的坐标为（2，0），在y轴上找一点Q，使点Q到点D的距离和到直线AB的距离之和最小，请求出最小值.‎ ‎ ‎ ‎2.对于平面直角坐标系x0y中的点平P（a，b），点的坐标为（其中k为常数，且k≠0），则称点为点P的“k属派生点”.‎ 例如：P（1，4）的“2属派生点”为（1+，2×1+4），即（3，6）．‎ ‎（1）①点P（-1，-2）的“2属派生点” 的坐标为 ____________； ‎ ‎ ②若点P的“k属派生点”的坐标为（3，3），请写出一个符合条件的点P的坐标____________；‎ ‎（2）若点P在x轴的正半轴上，点P的“k属派生点”为点，且△OP为等腰直角三角形，则k的值为________；‎ ‎（3）如图, 点Q的坐标为（0，），点A在函数的图象上，且点A是点B的“属派生点”，当线段B Q最短时，求B点坐标．‎ ‎ ‎ ‎（四）“三角形两边之差小于第三边” (线段差最大问题)‎ 1. 已知点A的坐标为（-4,8），点B的坐标为（2，2）,‎ (1) 如图（1）请在x轴上找到一点P，使最大，并求出此时P点的坐标。‎ ‎（2）如图（2）请在y轴上找到一点P，使最大，并求出此时P点的坐标。‎ 图2‎ 图1‎ ‎ ‎ 中考真题练习 ‎1.(2014年广东深圳)如图，在平面直角坐标系中，⊙M过原点O，与x轴交于A（4，0），与y轴交于B（0，3），点C为劣弧AO的中点，连接AC并延长到D，使DC=4CA，连接BD． ‎ ‎（1）求⊙M的半径； ‎ ‎（2）证明：BD为⊙M的切线； ‎ ‎（3）在直线MC上找一点P，使|DP﹣AP|最大． ‎ ‎ ‎ ‎ ‎ （五） 与圆有关的最值问题 （1） 利用“相切”解决最值问题 （2） 利用“直径是最长的弦”求最值 ‎（3）利用“对角互补存隐圆” 、“定弦定角存隐圆”、“定点定长存隐圆” 求最值 ‎1.（2013•枣庄）如图，已知线段OA交⊙O于点B，且OB=AB，点P是⊙O上的一个动点，那么∠OAP的最大值是（　　）‎ A．90° B．60° C．45° D．30°‎ ‎ ‎ ‎ 1题图 2题图 3题图 2. ‎（2016 广州天河一模）如图，AB为⊙O的弦，AB=6，点C是⊙O上的一个动 点，且∠ACB=45°，若点M，N分别是AB，BC的中点， 则线段MN长的最大值是 . ‎ ‎3.（2014•武汉模拟）如图，P为⊙O内的一个定点，A为⊙O上的一个动点，射线AP、AO分别与⊙O交于B、C两点．若⊙O的半径长为3，OP=，则弦BC的最大值为（　　）‎ ‎ A．2 B．3 C． D．3‎ ‎4. （2014春•兴化市月考）在平面直角坐标系中，点A的坐标为（3，0），点B为y轴正半轴上的一点，点C为第一象限内一点，且AC=2，设tan∠BOC=m，则m的取值范围是（　　）‎ ‎ A．m≥0 B． C． D．‎ ‎ ‎ ‎ 4题图 5题图 6题图 ‎ ‎5.（2015 花都一模）如图，E，F是正方形ABCD的边AD上两个动点，满足AE=DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是　　　　　　．‎ ‎6.（2013•内江）在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13，0），直线y=kx﹣3k+4与⊙O交于 ‎ B、C两点，则弦BC的长的最小值为　　　　　　．‎ 7. ‎（2015•泰兴市二模）如图，定长弦CD在以AB为直径的⊙O上滑动（点C、D与点A、B不重合），M是CD的中点，过点C作CP⊥AB于点P，若CD=3，AB=8，PM=l，则l的最大值是　　　　　　．‎ ‎ ‎ ‎ 7题图 8题图 9题图 ‎8.如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，点D是平面内的一个动点，且AD=2，M为BD的中点，在D点运动过程中，线段CM长度的取值范围是 .‎ ‎9. 正方形ABCD中，BC=4，E，F分别为射线BC，CD上两个动点，且满足BE=CF，设AE，BF交于G，则DG的最小值为 . ‎ ‎10.如图, 边长为3的等边△ABC, D、E分别为边BC、AC上的点, 且BD＝CE, AD、BE交于P点, 则CP的最小值为 .‎ ‎ ‎ ‎ ‎ ‎ 10题图 ‎11.（2015•安徽）在⊙O中，直径AB=6，BC是弦，∠ABC=30°，点P在BC上，点Q在⊙O上，且OP⊥PQ．‎ ‎（1）如图1，当PQ∥AB时，求PQ的长度；‎ ‎（2）如图2，当点P在BC上移动时，求PQ长的最大值.‎ ‎ ‎ 12. ‎（2016 合肥模拟）如图，直角△ABC内接于⊙O，∠C=90°，点P在弧AB上移动，P，C分别位于AB的异侧（P不与A，B重合），△PCD也为直角三角形，∠PCD=90°，且直角△PCD的斜边PD也经过点B，BA，PC相交于点E.‎ (1） 当BA平分∠PBC时，求的值；‎ (2） 已知：AC=1，BC=2，求△PCD面积的最大值。‎ ‎ ‎ 13. 在平面直角坐标系中，O为原点，点A（-2，0），点B（0，2），点E，点F分别为OA，OB的中点.‎ ‎ 若正方形OEDF绕点O顺时针旋转，得正方形OE’D’F’，若直线AE’与直线BF’相交于点P.‎ ‎（1）求∠PAO的最大值；‎ ‎（2）点P运动的路径长.‎ ‎ ‎ 巩固练习 1. 如图1，有一圆锥形粮堆，其正视图是边长为6m的正三角形ABC，粮堆母线AC的中点P处有一老鼠正在偷吃粮食，此时，小猫正在B处，它要沿圆锥侧面到达P处捕捉老鼠，则小猫所经过的最短路程是     m．(结果不取近似值) ‎ ‎ ‎ ‎ 1题图 2题图 3题图 ‎ ‎ ‎ 2. 如图2，有一圆柱体高为10cm，底面圆的半径为4cm， AA1、BB1为相对的两条母线。在AA1上有一个蜘蛛Q，QA=3cm；在BB1上有一只苍蝇P，PB1=2cm。蜘蛛沿圆柱体侧面爬到P点吃苍蝇，最短的路径是      cm.‎ ‎（结果用带π和根号的式子表示）‎ 3. ‎（深圳 福田模拟）如图，∠MON=20°，A为射线OM上一点，OA=4，D为射线ON上一点，OD=8，C为射线AM上任意一点，B是线段OD上任意一点，那么折线ABCD的长AB+BC+CD的最小值是 ______．‎ ‎4. （2010•苏州）如图，已知A、B两点的坐标分别为（2，0）、（0，2），⊙C的圆心坐标为（﹣1，0），半径为1．若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值是（　　）‎ ‎ A．2 B．1 C． D．‎ ‎ ‎ ‎ 4题图 5题图 6题图 ‎5.（2014春•兴化市校级月考）如图所示，已知A（1，y1），B（2，y2）为反比例函数y=图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是　　　　　　．‎ ‎6. （2013•武汉模拟）如图∠BAC=60°，半径长1的⊙O与∠BAC的两边相切，P为⊙O上一动点，以P为圆心，PA长为半径的⊙P交射线AB、AC于D、E两点，连接DE，则线段DE长度的最大值为（　　）‎ ‎ A．3 B．6 C． D．‎ ‎7.（2015年武汉中考）如图，△ABC、△EFG均是边长为2的等边三角形，点D是边BC、EF的中点，直线AG、FC相交于点M．当△EFG绕点D旋转时，线段BM长的最小值是 .‎ ‎8．（2013•日照）问题背景：‎ 如图（a），点A、B在直线l的同侧，要在直线l上找一点C，使AC与BC的距离之和最小，我们可以作出点B关于l的对称点B′，连接AB′与直线l交于点C，则点C即为所求．‎ ‎（1）实践运用：‎ 如图（b），已知，⊙O的直径CD为4，点A在⊙O上，∠ACD=30°，B为弧AD的中点，P为直径CD上一动点，则BP+AP的最小值为　　　　　　．‎ ‎（2）知识拓展：‎ 如图（c），在Rt△ABC中，AB=10，∠BAC=45°，∠BAC的平分线交BC于点D，E、F分别是线段AD和AB上的动点，求BE+EF的最小值，并写出解答过程．‎ ‎9. 如图，已知点A(-4，8)和点B(2，n)在抛物线y=ax2上． ‎ ‎（1）求a的值及点B关于x轴对称点P的坐标，并在x轴上找一点Q，使得AQ+QB最短，求出点Q的坐标； ‎ ‎（2）平移抛物线y=ax2，记平移后点A的对应点为A′，点B的对应点为B′，点C(-2，0)和点D(-4，0)是x轴上的两个定点． ‎ ‎① 当抛物线向左平移到某个位置时，A′C+CB′最短，求此时抛物线的函数解析式； ‎ ‎② 当抛物线向左或向右平移时，是否存在某个位置，使四边形A′B′CD的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由．‎ ‎ ‎ ‎ 备用图 ‎10. 已知：如图，AB是⊙O的直径，在AB的两侧有定点C和动点P，AB=5，AC=3．点P在上运动（点P不与A，B重合），CP交AB于点D，过点C作CP的垂线，与PB的延长线交于点Q．‎ ‎（1）求∠P的正切值；‎ ‎（2）当CP⊥AB时，求CD和CQ的长；‎ ‎（3）当点P运动到什么位置时，CQ取到最大值？求此时CQ的长．‎ ‎11.先阅读材料，再解答问题：‎ ‎ 小明同学在学习与圆有关的角时了解到：在同圆或等圆中，同弧（或等弧）所对的圆周角相等．如图，点A、B、C、D均为⊙O上的点，则有∠C=∠D．小明还发现，若点E在⊙O外，且与点D在直线AB同侧，则有∠D>∠E．‎ ‎ ‎ 请你参考小明得出的结论，解答下列问题：‎ ‎(1) 如图1，在平面直角坐标系xOy中，点A的坐标为(0,7)，点B的坐标为(0,3)，‎ ‎ 点C的坐标为(3,0) ．‎ ‎ ①在图1中作出△ABC的外接圆（保留必要的作图痕迹，不写作法）；‎ ‎②若在轴的正半轴上有一点D，且∠ACB =∠ADB，则点D的坐标为 ；‎ ‎ (2) 如图2，在平面直角坐标系xOy中，点A的坐标为(0,m)，点B的坐标为(0,n)，‎ 其中m>n>0．点P为轴正半轴上的一个动点，当∠APB达到最大时，直接写出此时点P的坐标．‎ ‎12. （8分）（2016•北京）在平面直角坐标系xOy中，点P的坐标为 ，点Q的坐标为 ，且 ，若P，Q为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P，Q的“相关矩形”，如图为点P，Q的“相关矩形”示意图．‎ ‎ （1）已知点A的坐标为（1，0），‎ ‎ ①若点B的坐标为（3，1），求点A，B的“相关矩形”的面积；‎ ‎ ②点C在直线x=3上，若点A，C的“相关矩形”为正方形，求直线AC的表达式；‎ ‎ （2）⊙O的半径为，点M的坐标为（m，3），若在⊙O上存在一点N，使得点M，N的“相关矩形”为正方形，求m的取值范围．‎ ‎ ‎ ‎ ‎