- 300.00 KB
- 2021-05-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
《中考数学复习模块4-圆》之典型中考题讲解
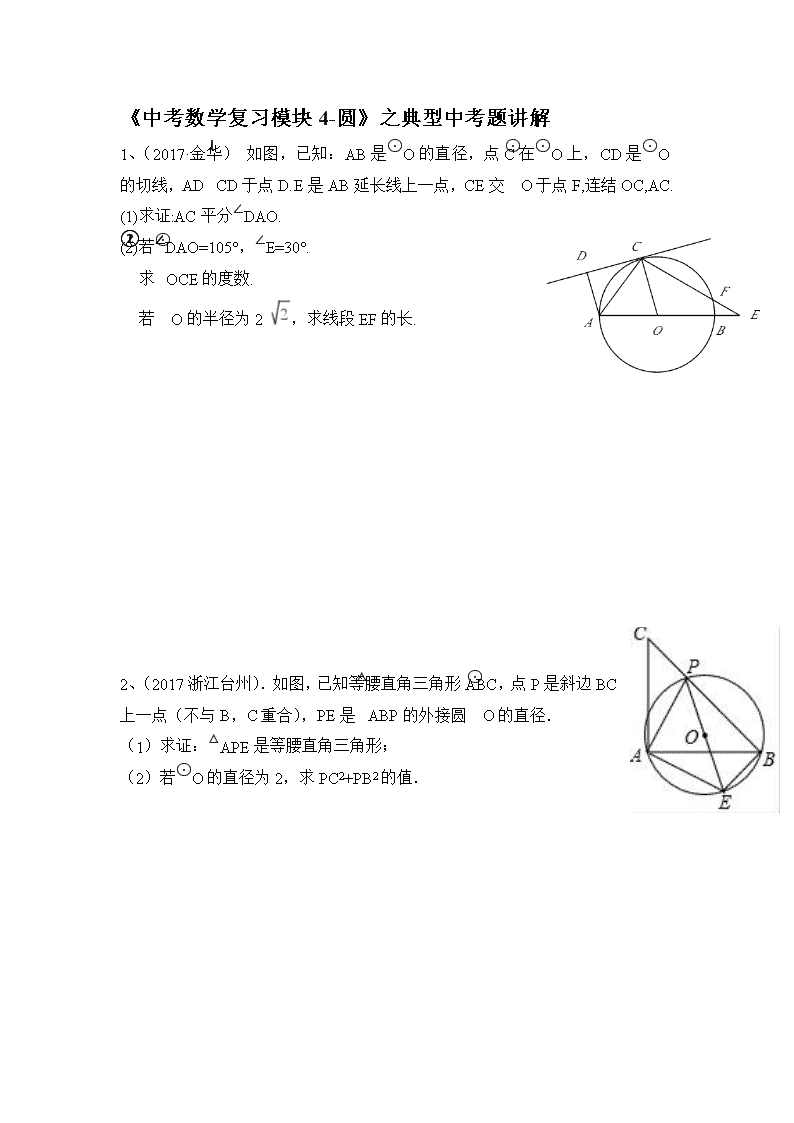
1、(2017·金华) 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为2 ,求线段EF的长.
2、(2017浙江台州).如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求PC2+PB2的值.
3、(2017山东枣庄).如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2,BF=2,求阴影部分的面积(结果保留π).
4、(2017山东聊城).如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.
5、(2017山东东营).如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE⊥AC;
(2)若DE+EA=8,⊙O的半径为10,求AF的长度.
6、(2017山东潍坊).如图,AB为半圆O的直径,AC是⊙O的一条弦,D为的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=6,求阴影区域的面积.(结果保留根号和π)
7、(2017江苏无锡).如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.
(1)求点P的坐标;
(2)求过点A和点E,且顶点在直线CD上的抛物线的函数表达式.
8、(2017江苏盐城).如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
(1)求证:BC是⊙F的切线;
(2)若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;
(3)试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.
9、(2017湖北襄阳).如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
(1)求证:EF是⊙O的切线;
(2)若DE=1,BC=2,求劣弧的长l.
10、(2017湖北恩施).如图,AB、CD是⊙O的直径,BE是⊙O的弦,且BE∥CD,过点C的切线与EB的延长线交于点P,连接BC.
(1)求证:BC平分∠ABP;
(2)求证:PC2=PB•PE;
(3)若BE﹣BP=PC=4,求⊙O的半径.
11、(2017湖北随州).如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
12、(2017湖北宜昌).已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D.B点在⊙O上,连接OB.
(1)求证:DE=OE;
(2)若CD∥AB,求证:四边形ABCD是菱形.
答案:
1、(1)解:∵直线与⊙O相切,
∴OC⊥CD;
又∵AD⊥CD,
∴AD//OC,
∴∠DAC=∠OCA;
又∵OC=OA,
∴∠OAC=∠OCA,
∴∠DAC=∠OAC;
∴AC平分∠DAO.
(2)解:①∵AD//OC,∠DAO=105°,
∴∠EOC=∠DAO=105°;
∵∠E=30°,
∴∠OCE=45°.
②作OG⊥CE于点G,可得FG=CG,
∵OC=2,∠OCE=45°.
∴CG=OG=2,
∴FG=2;
∵在RT△OGE中,∠E=30°,
∴GE=2,
∴EF=GE-FG=2-2.
2、(1)证明:∵AB=AC,∠BAC=90°,
∴∠C=∠ABC=45°,
∴∠AEP=∠ABP=45°,
∵PE是直径,
∴∠PAB=90°,
∴∠APE=∠AEP=45°,
∴AP=AE,
∴△PAE是等腰直角三角形.
(2)作PM⊥AC于M,PN⊥AB于N,则四边形PMAN是矩形,
∴PM=AN,
∵△PCM,△PNB都是等腰直角三角形,
∴PC=PM,PB=PN,
∴PC2+PB2=2(PM2+PN2)=2(AN2+PN2)=2PA2=PE2=22=4.
3、解:(1)BC与⊙O相切.
证明:连接OD.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
又∵OD=OA,
∴∠OAD=∠ODA.
∴∠CAD=∠ODA.
∴OD∥AC.
∴∠ODB=∠C=90°,即OD⊥BC.
又∵BC过半径OD的外端点D,
∴BC与⊙O相切.
(2)设OF=OD=x,则OB=OF+BF=x+2,
根据勾股定理得:OB2=OD2+BD2,即(x+2)2=x2+12,
解得:x=2,即OD=OF=2,
∴OB=2+2=4,
∵Rt△ODB中,OD=OB,
∴∠B=30°,
∴∠DOB=60°,
∴S扇形AOB==,
则阴影部分的面积为S△ODB﹣S扇形DOF=×2×2﹣=2﹣.
故阴影部分的面积为2﹣.
4、(1)证明:∵圆心O在BC上,
∴BC是圆O的直径,
∴∠BAC=90°,
连接OD,
∵AD平分∠BAC,
∴∠BAC=2∠DAC,
∵∠DOC=2∠DAC,
∴∠DOC=∠BAC=90°,即OD⊥BC,
∵PD∥BC,
∴OD⊥PD,
∵OD为圆O的半径,
∴PD是圆O的切线;
(2)证明:∵PD∥BC,
∴∠P=∠ABC,
∵∠ABC=∠ADC,
∴∠P=∠ADC,
∵∠PBD+∠ABD=180°,∠ACD+∠ABD=180°,
∴∠PBD=∠ACD,
∴△PBD∽△DCA;
(3)解:∵△ABC为直角三角形,
∴BC2=AB2+AC2=62+82=100,
∴BC=10,
∵OD垂直平分BC,
∴DB=DC,
∵BC为圆O的直径,
∴∠BDC=90°,
在Rt△DBC中,DB2+DC2=BC2,即2DC2=BC2=100,
∴DC=DB=5,
∵△PBD∽△DCA,
∴=,
则PB===.
5、(1)证明:∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC.
∵DE是⊙O的切线,OD是半径,
∴DE⊥OD,
∴DE⊥AC;
(2)如图,过点O作OH⊥AF于点H,则∠ODE=∠DEH=∠OHE=90°,
∴四边形ODEH是矩形,
∴OD=EH,OH=DE.
设AH=x.
∵DE+AE=8,OD=10,
∴AE=10﹣x,OH=DE=8﹣(10﹣x)=x﹣2.
在Rt△AOH中,由勾股定理知:AH2+OH2=OA2,即x2+(x﹣2)2=102,
解得x1=8,x2=﹣6(不合题意,舍去).
∴AH=8.
∵OH⊥AF,
∴AH=FH=AF,
∴AF=2AH=2×8=16.
6、(1)证明:连接OD,
∵D为的中点,
∴∠CAD=∠BAD,
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∵DE⊥AC,
∴∠E=90°,
∴∠CAD+∠EDA=90°,即∠ADO+∠EDA=90°,
∴OD⊥EF,
∴EF为半圆O的切线;
(2)解:连接OC与CD,
∵DA=DF,
∴∠BAD=∠F,
∴∠BAD=∠F=∠CAD,
又∵∠BAD+∠CAD+∠F=90°,
∴∠F=30°,∠BAC=60°,
∵OC=OA,
∴△AOC为等边三角形,
∴∠AOC=60°,∠COB=120°,
∵OD⊥EF,∠F=30°,
∴∠DOF=60°,
在Rt△ODF中,DF=6,
∴OD=DF•tan30°=6,
在Rt△AED中,DA=6,∠CAD=30°,
∴DE=DA•sin30,EA=DA•cos30°=9,
∵∠COD=180°﹣∠AOC﹣∠DOF=60°,
∴CD∥AB,
故S△ACD=S△COD,
∴S阴影=S△AED﹣S扇形COD=×9×3﹣π×62=﹣6π.
7、解:(1)如图,作EF⊥y轴于F,DC的延长线交EF于H.设H(m,n),则P(m,0),PA=m+3,PB=3﹣m.
∵EH∥AP,
∴△ACP∽△ECH,
∴===,
∴CH=2n,EH=2m=6,
∵CD⊥AB,
∴PC=PD=n,
∵PB∥HE,
∴△DPB ∽△DHE,
∴===,
∴=,
∴m=1,
∴P(1,0).
(2)由(1)可知,PA=4,HE=8,EF=9,
连接OP,在Rt△OCP中,PC==2,
∴CH=2PC=4,PH=6,
∴E(9,6),
∵抛物线的对称轴为CD,
∴(﹣3,0)和(5,0)在抛物线上,设抛物线的解析式为y=a(x+3)(x﹣5),把E(9,6)代入得到a=,
∴抛物线的解析式为y=(x+3)(x﹣5),即y=x2﹣x﹣.
8、(1)证明:连接EF,
∵AE平分∠BAC,
∴∠FAE=∠CAE,
∵FA=FE,
∴∠FAE=∠FEA,
∴∠FEA=∠EAC,
∴FE∥AC,
∴∠FEB=∠C=90°,即BC是⊙F的切线;
(2)解:连接FD,
设⊙F的半径为r,
则r2=(r﹣1)2+22,
解得,r=,即⊙F的半径为;
(3)解:AG=AD+2CD.
证明:作FR⊥AD于R,
则∠FRC=90°,又∠FEC=∠C=90°,
∴四边形RCEF是矩形,
∴EF=RC=RD+CD,
∵FR⊥AD,
∴AR=RD,
∴EF=RD+CD=AD+CD,
∴AG=2FE=AD+2CD.
9、(1)证明:连接OC,
∵OA=OC,
∴∠OAC=∠DAC,∴∠DAC=∠OCA,
∴AD∥OC,
∵∠AEC=90°,∴∠OCF=∠AEC=90°,
∴EF是⊙O的切线;
(2)连接OD,DC,
∵∠DAC=DOC,∠OAC=BOC,
∴∠DAC=∠OAC,
∵ED=1,DC=2,
∴sin∠ECD=,
∴∠ECD=30°,
∴∠OCD=60°,
∵OC=OD,
∴△DOC是等边三角形,
∴∠BOC=∠COD=60°,OC=2,
∴l==π.
10、解:(1)∵BE∥CD,
∴∠1=∠3,
又∵OB=OC,
∴∠2=∠3,
∴∠1=∠2,即BC平分∠ABP;
(2)如图,连接EC、AC,
∵PC是⊙O的切线,
∴∠PCD=90°,
又∵BE∥DC,
∴∠P=90°,
∴∠1+∠4=90°,
∵AB为⊙O直径,
∴∠A+∠2=90°,
又∠A=∠5,
∴∠5+∠2=90°,
∵∠1=∠2,
∴∠5=∠4,
∵∠P=∠P,
∴△PBC∽△PCE,
即PC2=PB•PE;
(3)∵BE﹣BP=PC=4,
∴BE=4+BP,
∵PC2=PB•PE=PB•(PB+BE),
∴42=PB•(PB+4+PB),即PB2+2PB﹣8=0,
解得:PB=2,
则BE=4+PB=6,
∴PE=PB+BE=8,
作EF⊥CD于点F,
∵∠P=∠PCF=90°,
∴四边形PCFE为矩形,
∴PC=FE=4,FC=PE=8,∠EFD=∠P=90°,
∵BE∥CD,
∴DE=BC,
在Rt△DEF和Rt△BCP中,
∴Rt△DEF≌Rt△BCP(HL),
∴DF=BP=2,
则CD=DF+CF=10,
∴⊙O的半径为5.
11、(1)证明:连接DE,OD.
∵BC相切⊙O于点D,
∴∠CDA=∠AED,
∵AE为直径,
∴∠ADE=90°,
∵AC⊥BC,
∴∠ACD=90°,
∴∠DAO=∠CAD,
∴AD平分∠BAC;
(2)∵在Rt△ABC中,∠C=90°,AC=BC,
∴∠B=∠BAC=45°,
∵BC相切⊙O于点D,
∴∠ODB=90°,
∴OD=BD,∴∠BOD=45°,
设BD=x,则OD=OA=x,OB=x,
∴BC=AC=x+1,
∵AC2+BC2=AB2,
∴2(x+1)2=(x+x)2,
∴x=,
∴BD=OD=,
∴图中阴影部分的面积=S△BOD﹣S扇形DOE=﹣=1﹣.
12、解:(1)如图,连接OD,
∵CD是⊙O的切线,
∴OD⊥CD,
∴∠2+∠3=∠1+∠COD=90°,
∵DE=EC,
∴∠1=∠2,
∴∠3=∠COD,
∴DE=OE;
(2)∵OD=OE,
∴OD=DE=OE,
∴∠3=∠COD=∠DEO=60°,
∴∠2=∠1=30°,
∵OA=OB=OE,OE=DE=EC,
∴OA=OB=DE=EC,
∵AB∥CD,
∴∠4=∠1,
∴∠1=∠2=∠4=∠OBA=30°,
∴△ABO≌△CDE,
∴AB=CD,
∴四边形A∴D是平行四边形,
∴∠DAE=∠DOE=30°,
∴∠1=∠DAE,
∴CD=AD,
∴▱ABCD是菱形.