2008重庆市中考数学试题及答案 12页

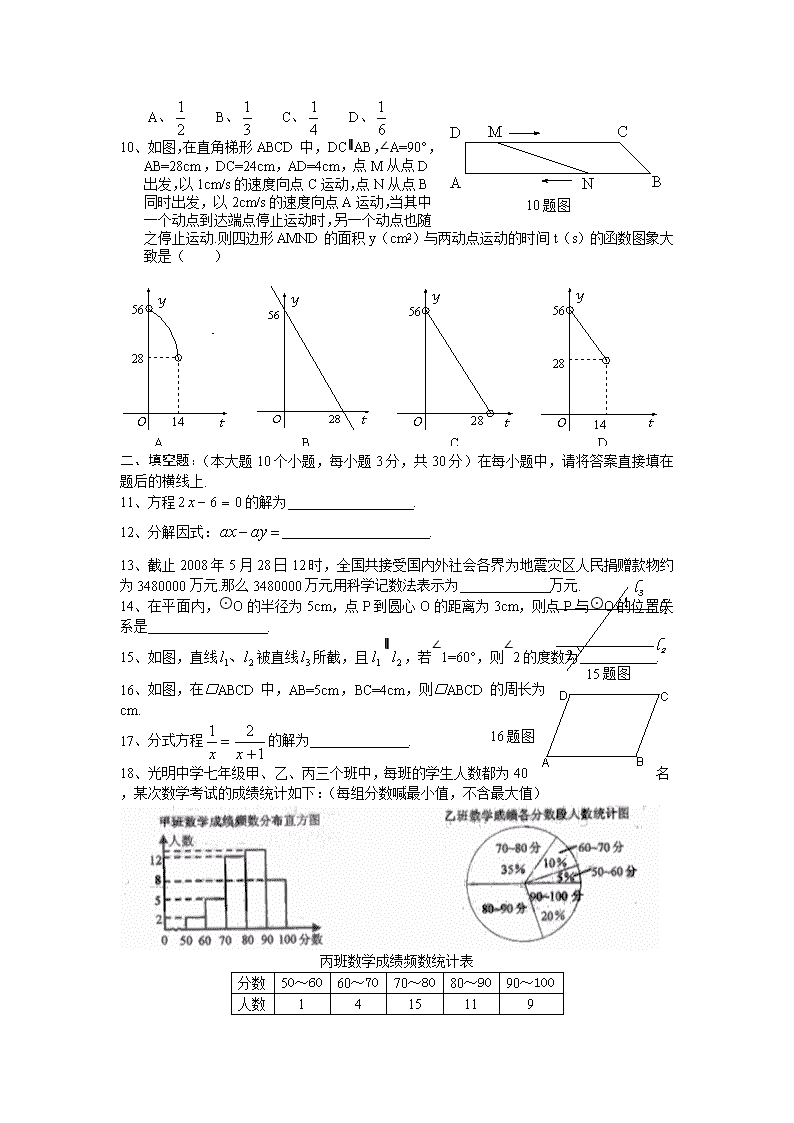
重庆市2008年初中毕业生学业暨高中招生考试 数 学 试 卷 ‎（本卷共四个大题 满分150分 考试时间120分钟）‎ 参考公式：抛物线的顶点坐标为，对称轴公式为 一、选择题（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将正确答案的代号填在题后的括号中.‎ ‎1、2的倒数是（ ）‎ A、 B、 C、 D、2‎ ‎2、计算的结果是（ ）‎ A、 B、 C、 D、‎ ‎3、不等式的解集在数轴上表示正确的是（ ）‎ ‎ A B C D ‎4、数据2，1，0，3，4的平均数是（ ）‎ A、0 B、‎1 C、2 D、3‎ ‎5、如图，AB是⊙O的直径，点C在⊙O上，则∠ACB的度数为（ ）‎ A、30° B、45° C、60° D、90°‎ ‎5题图 ‎6、如图是由4个大小相同的正方体搭成的几何体，其主视图是（ ）‎ 正面 ‎6题图 ‎7、计算的结果是（）‎ A、6 B、 C、2 D、‎ ‎8、若△ABC∽△DEF，△ABC与△DEF的相似比为2︰3，则S△ABC︰S△DEF为（）‎ A、2∶3 B、4∶‎9 C、∶ D、3∶2‎ ‎9、今年5月12日，四川汶川发生强烈地震后，我市立即抽调骨干医生组成医疗队赶赴灾区进行抗震救灾.某医院要从包括张医生在内的4名外科骨干医生中，随机地抽调2名医生参加抗震救灾医疗队，那么抽调到张医生的概率是（ ）‎ ‎10题图 A、 B、 C、 D、‎ ‎10、如图，在直角梯形ABCD中，DC∥AB，∠A=90°，AB=‎28cm，DC=‎24cm，AD=‎4cm，点M从点D出发，以‎1cm/s的速度向点C运动，点N从点B同时出发，以‎2cm/s的速度向点A运动，当其中一个动点到达端点停止运动时，另一个动点也随之停止运动.则四边形AMND的面积y（cm2）与两动点运动的时间t（s）的函数图象大致是（ ）‎ A B C D 二、填空题：（本大题10个小题，每小题3分，共30分）在每小题中，请将答案直接填在题后的横线上.‎ ‎11、方程的解为 .‎ ‎12、分解因式： .‎ ‎13、截止‎2008年5月28日12时，全国共接受国内外社会各界为地震灾区人民捐赠款物约为3480000万元.那么3480000万元用科学记数法表示为 万元.‎ ‎14、在平面内，⊙O的半径为‎5cm，点P到圆心O的距离为‎3cm，则点P与⊙O的位置关系是 .‎ ‎15题图 ‎15、如图，直线被直线所截，且∥，若∠1=60°，则∠2的度数为 .‎ ‎16、如图，在□ABCD中，AB=‎5cm，BC=‎4cm，则□ABCD的周长为 cm.‎ ‎16题图 ‎17、分式方程的解为 .‎ ‎18、光明中学七年级甲、乙、丙三个班中，每班的学生人数都为40名，某次数学考试的成绩统计如下：（每组分数喊最小值，不含最大值）‎ 丙班数学成绩频数统计表 分数 ‎50～60‎ ‎60～70‎ ‎70～80‎ ‎80～90‎ ‎90～100‎ 人数 ‎1‎ ‎4‎ ‎15‎ ‎11‎ ‎9‎ 根据以上图、表提供的信息，则80～90分这一组人数最多的班是 .‎ ‎19、如图①是一块瓷砖的图案，用这种瓷砖来铺设地面，如果铺成一个2×2的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个3×3的正方形图案（如图③），其中完整的圆共有13个，如果铺成一个4×4的正方形图案（如图④），其中完整的圆共有25个，若这样铺成一个10×10的正方形图案，则其中完整的圆共有 个.‎ ‎20题图 ‎19题图 ‎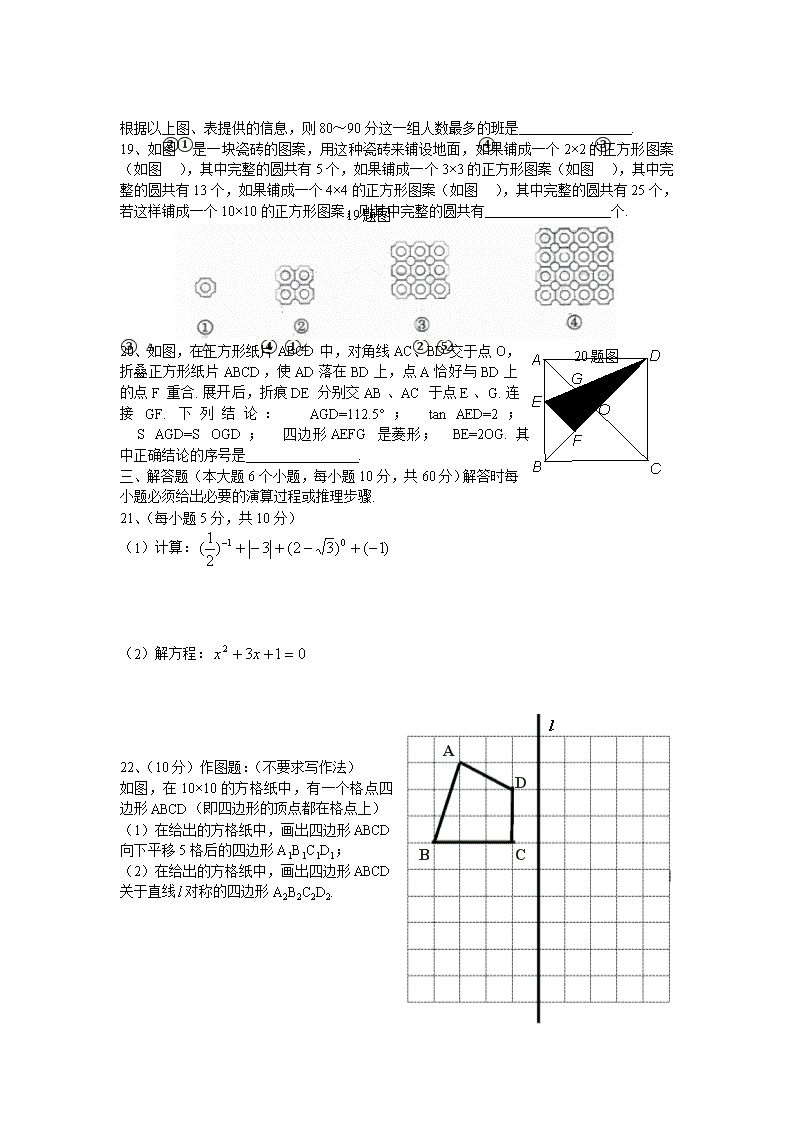20、如图，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合.展开后，折痕DE分别交AB、AC于点E、G.连接GF.下列结论：①∠AGD=112.5°；②tan∠AED=2；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG.其中正确结论的序号是 .‎ 三、解答题（本大题6个小题，每小题10分，共60分）解答时每小题必须给出必要的演算过程或推理步骤.‎ ‎21、（每小题5分，共10分）‎ ‎（1）计算：‎ ‎（2）解方程：‎ A B C D ‎22、（10分）作图题：（不要求写作法）‎ 如图，在10×10的方格纸中，有一个格点四边形ABCD（即四边形的顶点都在格点上）‎ ‎（1）在给出的方格纸中，画出四边形ABCD向下平移5格后的四边形A1B‎1C1D1；‎ ‎（2）在给出的方格纸中，画出四边形ABCD关于直线对称的四边形A2B‎2C2D2.‎ ‎23、（10分）先化简，再求值：‎ ‎24、（10分）已知：如图，反比例函数的图象经过点A、B，点A的坐标为（1，3），点B的纵坐标为1，点C的坐标为（2，0）.‎ ‎（1）求该反比例函数的解析式；‎ ‎（2）求直线BC的解析式.‎ ‎25、将背面完全相同，正面上分别写有数字1、2、3、4的四张卡片混合后，小明从中随机地抽取一张，把卡片上的数字做为被减数，将形状、大小完全相同，分别标有数字1、2、3的三个小球混合后，小华从中随机地抽取一个，把小球上的数字做为减数，然后计算出这两个数的差.‎ ‎（1）请你用画树状图或列表的方法，求这两数差为0的概率；‎ ‎（2）小明与小华做游戏，规则是：若这两数的差为非负数，则小明赢；否则，小华赢.你认为该游戏公平吗？请说明理由.如果不公平，请你修改游戏规则，使游戏公平.‎ ‎26题图 ‎26、（10分）已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF的延长线交DC于点E。‎ 求证：（1）△BFC≌△DFC；（2）AD=DE 四、解答题（本大题2个小题，每小题10分，共20分）解答时每小题必须给出必要的演算过程或推理步骤。‎ ‎27（10分）‎ 为支持四川抗震救灾，重庆市A、B、C三地现在分别有赈灾物资100吨，、100吨、80吨，需要全部运往四川重灾地区的D、E两县。根据灾区的情况，这批赈灾物资运往D县的数量比运往E县的数量的2倍少20吨。‎ ‎（1）求这批赈灾物资运往D、E两县的数量各是多少？‎ ‎（2）若要求C地运往D县的赈灾物资为60吨，A地运往D的赈灾物资为x吨（x为整数），B地运往D县的赈灾物资数量小于A地运往D县的赈灾物资数量的2倍。其余的赈灾物资全部运往E县，且B地运往E县的赈灾物资数量不超过25吨。则A、B两地的赈灾物资运往D、E两县的方案有几种？请你写出具体的运送方案；‎ ‎（3）已知A、B、C三地的赈灾物资运往D、E两县的费用如下表：‎ A地 B地 C地 运往D县的费用（元/吨）‎ ‎220‎ ‎200‎ ‎200‎ 运往E县的费用（元/吨）‎ ‎250‎ ‎220‎ ‎210‎ 为即使将这批赈灾物资运往D、E两县，某公司主动承担运送这批赈灾物资的总费用，在（2）问的要求下，该公司承担运送这批赈灾物资的总费用最多是多少？‎ ‎28、（10分）已知：如图，抛物线与y轴交于点C（0，4），与x轴交于点A、B，点A的坐标为（4，0）。‎ ‎（1）求该抛物线的解析式；‎ ‎（2）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ。当△CQE的面积最大时，求点Q的坐标；‎ ‎（3）若平行于x轴的动直线与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）。问：是否存在这样的直线，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由。‎ ‎28题图 重庆市2008年初中毕业生学业暨高中招生考试 数学试题参考答案及评分意见 一、选择题：ABCCD，ADBAD 二、填空题：11．； 12．； 13．；‎ 14．点在内； 15． 16．； 17．； 18．甲班；‎ ‎19．181； 20．①④⑤．‎ 三、解答题：‎ 21．解：（1）原式 （4分）‎ ‎． （5分）‎ ‎（2） （3分）‎ ‎． （5分）‎ 所以原方程的解为：，．‎ ‎22．解：作图如下：‎ ‎22题图 ‎（注：画正确一个给5分，共10分）‎ 23．解：原式 （2分）‎ ‎ （4分）‎ ‎ （7分）‎ ‎． （8分）‎ 当时，原式． （10分）‎ ‎24．解：（1）设所求反比例函数的解析式为：． （1分）‎ 点在此反比例函数的图象上，‎ ‎， （3分）‎ ‎． （4分）‎ 故所求反比例函数的解析式为：． （5分）‎ ‎（2）设直线的解析式为：． （6分）‎ 点的反比例函数的图象上，点的纵坐标为1，设，‎ ‎，．‎ 点的坐标为． （7分）‎ 由题意，得 （8分）‎ 解得： （9分）‎ 直线的解析式为：． （10分）‎ 25．解：（1）画树状图如下：‎ 被减数 减数 差 ‎ （4分）‎ 或列表如下：‎ 差 数 减 被减数 数减数 减减数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎2‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎0‎ ‎1‎ ‎ （4分）‎ 由图（表）知，所有可能出现的结果有12种，其中差为0的有3种，‎ 所以这两数的差为0的概率为：． （6分）‎ ‎（2）不公平． （7分）‎ 理由如下：‎ 由（1）知，所有可能出现的结果有12种，这两数的差为非负数的有9种，其概率为：，‎ 这两数的差为负数的概率为：． （9分）‎ 因为，所以该游戏不公平．‎ 游戏规则修改为：‎ 若这两数的差为正数，则小明赢；否则，小华赢． （10分）‎ 26．证明：（1）平分，． （1分）‎ 在和中，‎ ‎ （3分）‎ ‎． （4分）‎ ‎（2）连结． （5分）‎ ‎26题图 ‎，‎ ‎，‎ ‎． （6分）‎ ‎，．‎ ‎． （7分）‎ ‎，．‎ ‎，．‎ ‎． （8分）‎ 又是公共边，． （9分）‎ ‎． （10分）‎ 27．解：（1）设这批赈灾物资运往县的数量为吨，运往县的数量为吨． （1分）‎ 由题意，得 （2分）‎ 解得 （3分）‎ 答：这批赈灾物资运往县的数量为180吨，运往县的数量为100吨． （4分）‎ ‎（2）由题意，得 （5分）‎ 解得即．‎ 为整数，的取值为41，42，43，44，45． （6分）‎ 则这批赈灾物资的运送方案有五种．‎ 具体的运送方案是：‎ 方案一：地的赈灾物资运往县41吨，运往县59吨；‎ 地的赈灾物资运往县79吨，运往县21吨．‎ 方案二：地的赈灾物资运往县42吨，运往县58吨；‎ 地的赈灾物资运往县78吨，运往县22吨．‎ 方案三：地的赈灾物资运往县43吨，运往县57吨；‎ 地的赈灾物资运往县77吨，运往县23吨．‎ 方案四：地的赈灾物资运往县44吨，运往县56吨；‎ 地的赈灾物资运往县76吨，运往县24吨．‎ 方案五：地的赈灾物资运往县45吨，运往县55吨；‎ 地的赈灾物资运往县75吨，运往县25吨．‎ ‎ （7分）‎ ‎（3）设运送这批赈灾物资的总费用为元．由题意，得 ‎． （9分）‎ 因为随的增大而减小，且，为整数．‎ 所以，当时，有最大值．则该公司承担运送这批赈灾物资的总费用最多为：‎ ‎（元）． （10分）‎ ‎28．解：（1）由题意，得 （1分）‎ 解得 （2分）‎ 所求抛物线的解析式为：． （3分）‎ ‎（2）设点的坐标为，过点作轴于点．‎ 由，得，．‎ 点的坐标为． （4分）‎ ‎，．‎ ‎28题图 ‎，．，‎ 即．． （5分）‎ ‎ （6分）‎ ‎．‎ 又，‎ 当时，有最大值3，此时． （7分）‎ ‎（3）存在．‎ 在中．‎ ‎（ⅰ）若，，．‎ 又在中，，．．‎ ‎．此时，点的坐标为．‎ 由，得，．‎ 此时，点的坐标为：或． （8分）‎ ‎（ⅱ）若，过点作轴于点，‎ 由等腰三角形的性质得：，，‎ 在等腰直角中，．．‎ 由，得，．‎ 此时，点的坐标为：或． （9分）‎ ‎（ⅲ）若，，且，‎ 点到的距离为，而，‎ 此时，不存在这样的直线，使得是等腰三角形． （10分）‎ 综上所述，存在这样的直线，使得是等腰三角形．所求点的坐标为：‎ 或或或