2015中考数学新定义型问题训练 22页

专题知识突破二 新定义型问题 一、中考专题诠释 所谓“新定义”型问题，主要是指在问题中定义了中学数学中没有学过的一些概念、新 运算、新符号，要求学生读懂题意并结合已有知识、能力进行理解，根据新定义进行运算、 推理、迁移的一种题型.“新定义”型问题成为近年来中考数学压轴题的新亮点.在复习中应 重视学生应用新的知识解决问题的能力 二、解题策略和解法精讲 “新定义型专题”关键要把握两点：一是掌握问题原型的特点及其问题解决的思想方法； 二是根据问题情景的变化，通过认真思考，合理进行思想方法的迁移． 三、中考典例剖析 考点一：规律题型中的新定义 例 1 （ 2014• 济 南 ） 现 定 义 一 种 变 换 ： 对 于 一 个 由 有 限 个 数 组 成 的 序 列 S0， 将 其 中 的 每 个 数 换 成 该 数 在 S0 中 出 现 的 次 数 ，可得 到 一 个 新 序 列 S1，例如 序 列 S0： （ 4， 2， 3， 4， 2） ， 通 过 变 换 可 生 成 新 序 列 S 1： （ 2， 2， 1， 2， 2） ， 若 S 0 可 以 为 任 意 序 列 ， 则 下 面 的 序 列 可 作 为 S1 的 是 （ 　 　 ） A． （ 1， 2， 1， 2， 2） 　 　B． 　 （ 2， 2， 2， 3， 3） C． （ 1， 1， 2， 2， 3） 　 　D．（1，2，1，1，2） 思路分析：根 据 题 意 可 知 ， S1 中 2 有 2 的 倍 数 个 ， 3 有 3 的 倍 数 个 ， 据 此 即 可 作 出 选 择 ． 考点二：运算题型中的新定义 例 2 （ 2014• 铜 仁 ） 定 义 一 种 新 运 算 ： a⊗ b=b 2-ab， 如 ： 1⊗ 2=2 2-1× 2=2， 则 （ -1 ⊗ 2） ⊗ 3=_______. 思路分析：先 根 据 新 定 义 计 算 出 -1⊗ 2=6， 然 后 计 算 再 根 据 新 定 义 计 算 6⊗ 3 即 可 ． 考点三：探索题型中的新定义 例 3 （2013•钦州）定义：直线 l1 与 l2 相交于点 O，对于平面内任意一点 M，点 M 到直 线 l1、l2 的距离分别为 p、q，则称有序实数对（p，q）是点 M 的“距离坐标”，根据上述定 义，“距离坐标”是（1，2）的点的个数是（　　） A．2 B．3 C．4 D．5 思路分析： “距离坐标”是（1，2）的点表示的含义是该点到直线 l1、l2 的距离分别为 1、 2．由于到直线 l1 的距离是 1 的点在与直线 l1 平行且与 l1 的距离是 1 的两条平行线 a1、a2 上， 到直线 l2 的距离是 2 的点在与直线 l2 平行且与 l2 的距离是 2 的两条平行线 b1、b2 上，它们 有 4 个交点，即为所求． 考点四：开放题型中的新定义 例 4 （ 2014• 北 京 ） 对 某 一 个 函 数 给 出 如 下 定 义 ： 若 存 在 实 数 M＞ 0， 对 于 任 意 的 函 数 值 y，都 满 足 -M≤ y≤ M，则 称 这 个 函 数 是 有 界 函 数 ，在 所 有 满 足 条 件 的 M 中 ，其 最 小 值 称 为 这 个 函 数 的 边 界 值 ．例 如 ，如 图 中 的 函 数 是 有 界 函 数 ，其 边 界 值 是 1． （ 1） 分 别 判 断 函 数 y= （ x＞ 0） 和 y=x+1（ -4≤ x≤ 2） 是 不 是 有 界 函 数 ？ 若 是 有 界 函 数 ， 求 其 边 界 值 ； （ 2）若函 数 y=-x+1（ a≤ x≤ b， b＞ a）的边 界 值 是 2， 且 这 个 函 数 的 最 大 值 也 是 2， 求 b 的 取 值 范 围 ； （ 3） 将 函 数 y=x 2（ -1≤ x≤ m， m≥ 0） 的 图 象 向 下 平 移 m 个 单 位 ， 得 到 的 函 数 的 边 界 值 是 t， 当 m 在 什 么 范 围 时 ， 满 足 ≤ t≤ 1？ 思路分析：（ 1） 根 据 有 界 函 数 的 定 义 和 函 数 的 边 界 值 的 定 义 进 行 答 题 ； （ 2） 根 据 函 数 的 增 减 性 、 边 界 值 确 定 a=-1； 然 后 由 “ 函 数 的 最 大 值 也 是 2” 来 求 b 的 取 值 范 围 ； （ 3） 需 要 分 类 讨 论 ： m＜ 1 和 m≥ 1 两 种 情 况 ． 由 函 数 解 析 式 得 到 该 函 数 图 象 过 点 （ -1， 1） 、 （ 0， 0） ， 根 据 平 移 的 性 质 得 到 这 两 点 平 移 后 的 坐 标 分 别 是 （ -1， 1-m） 、 （ 0， -m） ； 最 后 由 函 数 边 界 值 的 定 义 列 出 不 等 式 ≤ 1-m≤ 1 或 -1≤ -m≤ - ， 易 求 m 取 值 范 围 ： 0≤ m≤ 或 ≤ m≤ 1． 考点五：阅读材料题型中的新定义 例 5 （ 2014• 乐 山 ） 对 于 平 面 直 角 坐 标 系 中 任 意 两 点 P 1 （ x1 ， y1 ） 、 P2 （ x2 ， y2） ， 称 |x1-x2|+|y1-y2|为 P 1、 P2 两 点 的 直 角 距 离 ， 记 作 ： d（ P 1， P2） ． 若 P0 （ x0， y0）是 一 定 点 ， Q（ x， y）是 直 线 y=kx+b 上 的 一 动 点 ， 称 d（ P 0， Q）的 最 小 值 为 P0 到 直 线 y=kx+b 的 直 角 距 离 ． 令 P0（ 2， -3） ， O 为 坐 标 原 点 ． 则 ： （ 1） d（ O， P 0） =_________； （ 2） 若 P（ a， -3） 到 直 线 y=x+1 的 直 角 距 离 为 6， 则 a=__________． 思路分析：（ 1） 根 据 题 中 所 给 出 的 两 点 的 直 角 距 离 公 式 即 可 得 出 结 论 ； （ 2） 先 根 据 题 意 得 出 关 于 x 的 式 子 ， 再 由 绝 对 值 的 几 何 意 义 即 可 得 出 结 论 ． 四、中考真题演练 一、选择题 1．（ 2014• 大 庆 ） 对 坐 标 平 面 内 不 同 两 点 A（ x 1， y1） 、 B（ x 2， y2） ， 用 |AB|表 示 A、B 两 点 间 的 距 离（ 即 线 段 AB 的 长 度 ），用 ‖ AB‖ 表 示 A、B 两 点 间 的 格 距 ， 定 义 A、B 两 点 间 的 格 距 为 ‖ AB‖ =|x 1-x2|+|y1-y2|，则 |AB|与 ‖ AB‖ 的 大 小 关 系 为 （ 　 　 ） A．|AB|≥‖AB‖ B．|AB|＞‖AB‖ C．|AB|≤‖AB‖ D．|AB|＜‖AB‖ 2．（ 2014• 龙 岩 ）定 义 符 号 min{a， b}的 含 义 为 ： 当 a≥ b 时 min{a， b}=b； 当 a ＜ b 时 min{a， b}=a． 如 ： min{1， -3}=-3， min{-4， -2}=-4． 则 min{-x 2+1， -x} 的 最 大 值 是 （ 　 　 ） 1 x 3 4 3 4 3 4 1 4 3 4 A． B． C．1 D．0 3．（ 2014• 泰 州 ）如果 三 角 形 满 足 一 个 角 是 另 一 个 角 的 3 倍 ，那 么 我 们 称 这 个 三 角 形 为“ 智 慧 三 角 形 ” ．下 列 各 组 数 据 中 ，能 作 为 一 个 智 慧 三 角 形 三 边 长 的 一 组 是 （ 　 　 ） A．1，2，3 B．1，1， C．1，1， D．1，2， 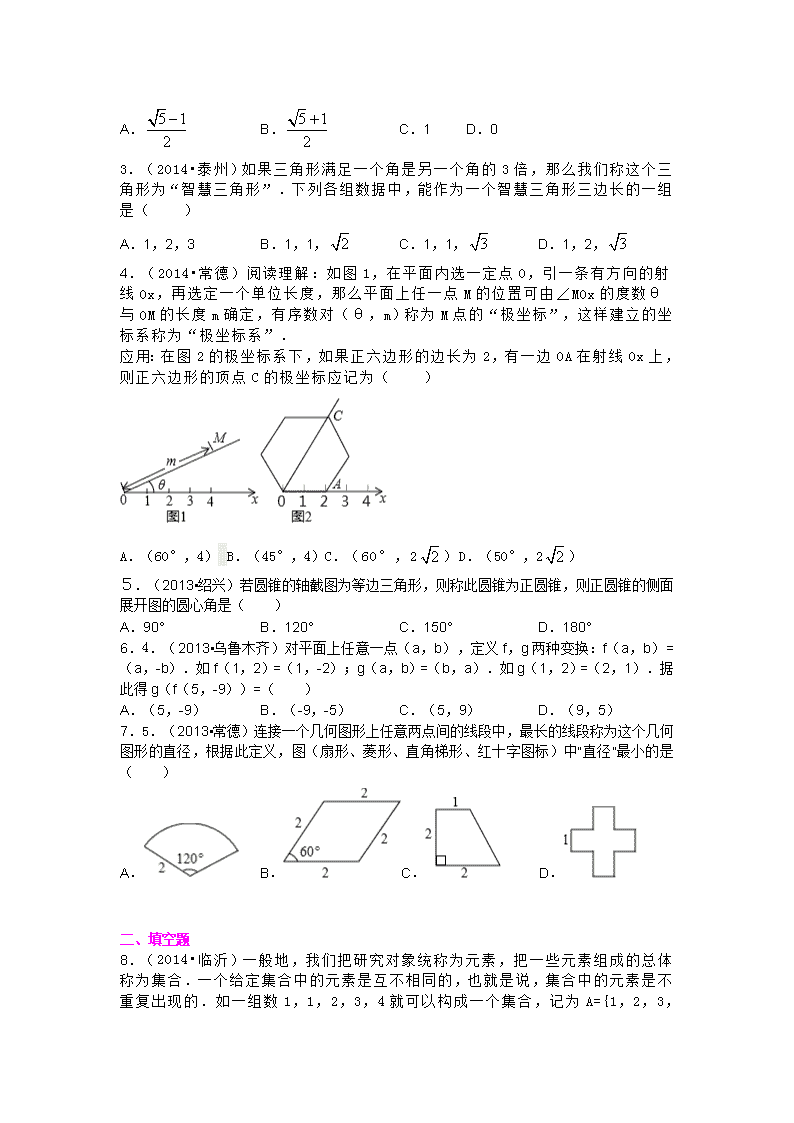4．（ 2014• 常 德 ） 阅 读 理 解 ： 如 图 1， 在 平 面 内 选 一 定 点 O， 引 一 条 有 方 向 的 射 线 Ox， 再 选 定 一 个 单 位 长 度 ， 那 么 平 面 上 任 一 点 M 的 位 置 可 由 ∠ MOx 的 度 数 θ 与 OM 的 长 度 m 确 定 ， 有 序 数 对 （ θ ， m）称为 M 点 的 “ 极 坐 标 ”，这 样 建 立 的 坐 标 系 称 为 “ 极 坐 标 系 ” ． 应 用：在图 2 的 极 坐 标 系 下 ，如 果 正 六 边 形 的 边 长 为 2，有 一 边 OA 在 射 线 Ox 上 ， 则 正 六 边 形 的 顶 点 C 的 极 坐 标 应 记 为 （ 　 　 ） A．（60°，4） B．（45°，4）C．（ 60° ， 2 ） D．（50°，2 ） ５．（2013•绍兴）若圆锥的轴截图为等边三角形，则称此圆锥为正圆锥，则正圆锥的侧面 展开图的圆心角是（　　） A．90° B．120° C．150° D．180° 6．4．（2013•乌鲁木齐）对平面上任意一点（a，b），定义 f，g 两种变换：f（a，b）= （a，-b）．如 f（1，2）=（1，-2）；g（a，b）=（b，a）．如 g（1，2）=（2，1）．据 此得 g（f（5，-9））=（　　） A．（5，-9） B．（-9，-5） C．（5，9） D．（9，5） 7．5．（2013•常德）连接一个几何图形上任意两点间的线段中，最长的线段称为这个几何 图形的直径，根据此定义，图（扇形、菱形、直角梯形、红十字图标）中“直径”最小的是 （　　） A． B． C． D． 二、填空题 8．（ 2014• 临 沂 ）一般 地 ，我 们 把 研 究 对 象 统 称 为 元 素 ，把 一 些 元 素 组 成 的 总 体 称 为 集 合 ．一 个 给 定 集 合 中 的 元 素 是 互 不 相 同 的 ，也 就 是 说 ，集 合 中 的 元 素 是 不 重 复 出 现 的 ．如 一 组 数 1，1，2，3，4 就 可 以 构 成 一 个 集 合 ，记 为 A={1，2，3， 5 1 2 − 5 1 2 + 2 3 3 2 2 4}． 类 比 实 数 有 加 法 运 算 ， 集 合 也 可 以 “ 相 加 ” ． 定 义：集合 A 与 集 合 B 中 的 所 有 元 素 组 成 的 集 合 称 为 集 合 A 与 集 合 B 的 和 ，记 为 A+B．若 A={-2，0，1，5，7}， B={-3， 0， 1， 3， 5}， 则 A+B=___________． 9 ． （ 2014 • 新 疆 ） 规 定 用 符 号 [x] 表 示 一 个 实 数 的 整 数 部 分 ， 例 如 [3.69]=3． [ ]=1， 按 此 规 定 ， [ -1]＝ 　 　　　　 ． 10．（ 2014• 北 京 ） 在 平 面 直 角 坐 标 系 xOy 中 ， 对 于 点 P（ x， y） ， 我 们 把 点 P （ -y+1， x+1） 叫 做 点 P′ 伴 随 点 ． 已 知 点 A 1 的 伴 随 点 为 A2， 点 A2 的 伴 随 点 为 A3，点 A3 的 伴 随 点 为 A4， … ，这 样 依 次 得 到 点 A1，A 2，A 3， … ，A n， … ．若 点 A1 的 坐 标 为 （ 3， 1） ， 则 点 A 3 的 坐 标 为 ______， 点 A2014 的 坐 标 为 _______； 若 点 A1 的 坐 标 为 （ a， b） ， 对 于 任 意 的 正 整 数 n， 点 A n 均 在 x 轴 上 方 ， 则 a， b 应 满 足 的 条 件 为 __________． 11．（ 2014• 荆 州 ） 我 们 知 道 ， 无 限 循 环 小 数 都 可 以 转 化 为 分 数 ． 例 如 ： 将 转 化 为 分 数 时 ， 可 设 =x， 则 x=0.3+ x， 解 得 x= ， 即 = ． 仿 此 方 法 ， 将 化 成 分 数 是 　 　　　　 ． 12． （ 2014• 塘 沽 区 二 模 ） 如 图 1， 把 一 张 标 准 纸 一 次 又 一 次 对 开 ， 得 到 “ 2 开 ” 纸 、“ 4 开 ”纸、“ 8 开 ”纸、“ 16 开 ”纸、 … ，已 知 标 准 纸 的 短 边 长 为 a．（ 说 明：①标 准 纸“ 2 开 ”纸、“ 4 开 ”纸、“ 8 开 ”纸、“ 16 开 ”纸、 … 都 是 矩 形；② 本 题 中 所 求 边 长 或 面 积 都 用 含 a 的 代 数 式 表 示 ． ） （ Ⅰ ） 如 图 2， 把 上 面 对 开 得 到 的 “ 16 开 ” 纸 按 如 下 步 骤 折 叠 ： 第 一 步 ： 将 矩 形 的 短 边 AB 与 长 边 AD 对 齐 折 叠 ， 点 B 落 在 AD 上 的 点 B′ 处 ， 铺 平 后 得 折 痕 AE； 第 二 步 ： 将 长 边 AD 与 折 痕 AE 对 齐 折 叠 ， 点 D 正 好 与 点 E 重 合 ， 铺 平 后 得 折 痕 AF． 则 AD： AB 的 值 是 　 　　　　 ； （ Ⅱ ） 求 “ 2 开 ” 纸 长 与 宽 的 比 ； （ Ⅲ ） 如 图 3， 由 8 个 大 小 相 等 的 小 正 方 形 构 成 “ L” 型 图 案 ， 它 的 四 个 顶 点 E， F， G， H 分 别 在 “ 16 开 ” 纸 的 边 AB， BC， CD， DA 上 ， 则 DG 的 长 . 13． （2014•连云港）如图 1，折线段 AOB 将面积为 S 的⊙O 分成两个扇形，大扇形、小扇 形的面积分别为 S1、S2，若 =0.618，则称分成的小扇形为“黄金扇形”．生活中的 折扇（如图 2）大致是“黄金扇形”，则“黄金扇形”的圆心角约为 _______．（精确到 0.1） 13 13 0.3 • 0.3 • 1 10 1 3 0.3 • 1 3 0.45 • • 1 2 1 S S S S = 14．（2013•上海）当三角形中一个内角 α 是另一个内角 β 的两倍时，我们称此三角形为“特 征三角形”，其中 α 称为“特征角”．如果一个“特征三角形”的“特征角”为 100°，那么这个“特 征三角形”的最小内角的度数为 ． 三、解答题 15．（2014•厦门）当 m，n 是正实数，且满足 m+n=mn 时，就称点 P（m， ）为“完美 点”，已知点 A（0，5）与点 M 都在直线 y=-x+b 上，点 B，C 是“完美点”，且点 B 在线段 AM 上，若 MC= ，AM=4 ，求△MBC 的面积． 16．（ 2014• 白 银 ） 阅 读 理 解 ： 我 们 把 称 作 二 阶 行 列 式 ， 规 定 他 的 运 算 法 则 为 =ad-bc． 如 =2× 5-3× 4=-2． 如 果 有 ＞ 0， 求 x 的 解 集 ． 17．（ 2014• 漳 州 ）如 图 ， △ ABC 中 ， AB=AC， ∠ A=36° ， 称 满 足 此 条 件 的 三 角 形 为 黄 金 等 腰 三 角 形 ． 请 完 成 以 下 操 作：（画 图 不 要 求 使 用 圆 规 ， 以 下 问 题 所 指 的 等 腰 三 角 形 个 数 均 不 包 括 △ ABC） （ 1） 在 图 1 中 画 1 条 线 段 ， 使 图 中 有 2 个 等 腰 三 角 形 ， 并 直 接 写 出 这 2 个 等 腰 三 角 形 的 顶 角 度 数 分 别 是 _____度 和 ______度 ； （ 2） 在 图 2 中 画 2 条 线 段 ， 使 图 中 有 4 个 等 腰 三 角 形 ； （ 3） 继 续 按 以 上 操 作 发 现 ： 在 △ ABC 中 画 n 条 线 段 ， 则 图 中 有 ____个 等 腰 三 角 形 ， 其 中 有 ________个 黄 金 等 腰 三 角 形 ． 18．（2013•北京）对于平面直角坐标系 xOy 中的点 P 和⊙C，给出如下的定义：若⊙C 上 存在两个点 A、B，使得∠APB=60°，则称 P 为⊙C 的关联点．已知点 D（ ， ）， E（0，-2），F（2 ，0）． （1）当⊙O 的半径为 1 时， ①在点 D、E、F 中，⊙O 的关联点是 ． ②过点 F 作直线 l 交 y 轴正半轴于点 G，使∠GFO=30°，若直线 l 上的点 P（m，n）是⊙O 的关联点，求 m 的取值范围； （2）若线段 EF 上的所有点都是某个圆的关联点，求这个圆的半径 r 的取值范围． m n 3 2 a b c d a b c d 2 3 4 5 2 3 1 x x − 1 2 1 2 3 19．（ 2014• 山 西 ） 阅 读 以 下 材 料 ， 并 按 要 求 完 成 相 应 的 任 务 ． 几 何 中 ， 平 行 四 边 形 、 矩 形 、 菱 形 、 正 方 形 和 等 腰 梯 形 都 是 特 殊 的 四 边 形 ， 大 家 对 于 它 们 的 性 质 都 非 常 熟 悉 ， 生 活 中 还 有 一 种 特 殊 的 四 边 形 --筝 形 ． 所 谓 筝 形 ， 它 的 形 状 与 我 们 生 活 中 风 筝 的 骨 架 相 似 ． 定 义：两 组 邻 边 分 别 相 等 的 四 边 形 ， 称 之 为 筝 形 ， 如 图 ， 四 边 形 ABCD 是 筝 形 ， 其 中 AB=AD， CB=CD 判 定 ： ① 两 组 邻 边 分 别 相 等 的 四 边 形 是 筝 形 ② 有 一 条 对 角 线 垂 直 平 分 另 一 条 对 角 线 的 四 边 形 是 筝 形 显 然 ， 菱 形 是 特 殊 的 筝 形 ， 就 一 般 筝 形 而 言 ， 它 与 菱 形 有 许 多 相 同 点 和 不 同 点 如 果 只 研 究 一 般 的 筝 形 （ 不 包 括 菱 形 ） ， 请 根 据 以 上 材 料 完 成 下 列 任 务 ： （ 1） 请 说 出 筝 形 和 菱 形 的 相 同 点 和 不 同 点 各 两 条 ； （ 2）请仿 照 图 1 的 画 法 ，在 图 2 所 示 的 8× 8 网 格 中 重 新 设 计 一 个 由 四 个 全 等 的 筝 形 和 四 个 全 等 的 菱 形 组 成 的 新 图 案 ， 具 体 要 求 如 下 ： ① 顶 点 都 在 格 点 上 ； ② 所 涉 及 的 图 案 既 是 轴 对 称 图 形 又 是 中 心 对 称 图 形 ； ③ 将 新 图 案 中 的 四 个 筝 形 都 图 上 阴 影 （ 建 议 用 一 系 列 平 行 斜 线 表 示 阴 影 ） ． 20．（ 2014• 黔 西 南 州 ）已知 点 P（ x 0，y0）和直 线 y=kx+b，则 点 P 到 直 线 y=kx+b 的 距 离 d 可 用 公 式 d= 计 算 ． 例 如 ： 求 点 P（ -2， 1） 到 直 线 y=x+1 的 距 离 ． 解 ： 因 为 直 线 y=x+1 可 变 形 为 x-y+1=0， 其 中 k=1， b=1． 所 以 点 P（ -2，1）到直 线 y=x+1 的 距 离 为 d= = = . 根 据 以 上 材 料 ， 求 ： 0 0 21 kx y b k − + + 0 0 2 | | 1 kx y b k − + + ( ) 2 | 1 -2 -1+1 | 1+1 × 2 = 2 2 （ 1） 点 P（ 1， 1） 到 直 线 y=3x-2 的 距 离 ， 并 说 明 点 P 与 直 线 的 位 置 关 系 ； （ 2） 点 P（ 2， -1） 到 直 线 y=2x-1 的 距 离 ； （ 3） 已 知 直 线 y=-x+1 与 y=-x+3 平 行 ， 求 这 两 条 直 线 的 距 离 ． 21． （2014•抚州）【试题背景】 已知：l∥m∥n∥k，平行线 l 与 m、m 与 n、n 与 k 之间的距离分别为 d 1、d2、d3，且 d1=d3=1，d2=2．我们把四个顶点分别在 l、m、n、k 这四条平行线上的四边形称为“格线四 边形”． 【探究 1】 （1）如图 1，正方形 ABCD 为“格线四边形”，BE⊥l 于点 E，BE 的反向延长线交直线 k 于 点 F，求正方形 ABCD 的边长． 【探究 2】 （2）矩形 ABCD 为“格线四边形”，其长：宽=2：1，则矩形 ABCD 的宽为　　　　　．（直 接写出结果即可） 【探究 3】 如图 2，菱形 ABCD 为“格线四边形”且∠ADC=60°，△AEF 是等边三角形，AE⊥k 于点 E， ∠AFD=90°，直线 DF 分别交直线 l、k 于点 G、点 M．求证：EC=DF． 【拓展】 （4）如图 3，l∥k，等边△ABC 的顶点 A、B 分别落在直线 l、k 上，AB⊥k 于点 B，且 AB=4，∠ACD=90°，直线 CD 分别交直线 l、k 于点 G、点 M、点 D、点 E 分别是线段 GM、BM 上的动点，且始终保持 AD=AE，DH⊥l 于点 H． 猜想：DH 在什么范围内，BC∥DE？并说明此时 BC∥DE 的理由． 22．（2014•顺义区一模）设 p，q 都是实数，且 p＜q．我们规定：满足不等式 p≤x≤q 的 实数 x 的所有取值的全体叫做闭区间，表示为[p，q]．对于一个函数，如果它的自变量 x 与 函数值 y 满足：当 p≤x≤q 时，有 p≤y≤q，我们就称此函数是闭区间[p，q]上的“闭函 数”． （1）反比例函数 y= 是闭区间[1，2014]上的“闭函数”吗？请判断并说明理由； （2）若一次函数 y=kx+b（k≠0）是闭区间[m，n]上的“闭函数”，求此函数的解析式； （3）若实数 c，d 满足 c＜d，且 d＞2，当二次函数 y= x2-2x 是闭区间[c，d]上的“闭函 数”时，求 c，d 的值． 23．（ 2014• 佛 山 ） 我 们 把 “ 按 照 某 种 理 想 化 的 要 求 （ 或 实 际 可 能 应 用 的 标 准 ） 来 反 映 或 概 括 的 表 现 某 一 类 或 一 种 事 物 关 系 结 构 的 数 学 形 式 ” 看 作 是 一 个 数 学 中 的 一 个 “ 模 式 ” （ 我 国 著 名 数 学 家 徐 利 治 ） ． 如 图 是 一 个 典 型 的 图 形 模 式 ，用它 可 测 底 部 可 能 达 不 到 的 建 筑 物 的 高 度 ，用它 可 测 河 宽 ， 用 它 可 解 决 数 学 中 的 一 些 问 题 ． 等 等 ． （ 1） 如 图 ， 若 B 1B=30 米 ， ∠ B1=22° ， ∠ ABC=30° ， 求 AC（ 精 确 到 1） ； 2014 x 1 2 （ 参 考 数 据 ： sin22° ≈ 0.37， cos22° ≈ 0.92， tan22° ≈ 0.40， ≈ 1.73） （ 2） 如 图 2， 若 ∠ ABC=30° ， B 1B=AB， 计 算 tan15° 的 值 （ 保 留 准 确 值 ） ； （ 3） 直 接 写 出 tan7.5° 的 值 ． （ 注 ： 若 出 现 双 重 根 式 ， 则 无 需 化 简 ） 24．（ 2014• 安 徽 ） 若 两 个 二 次 函 数 图 象 的 顶 点 、 开 口 方 向 都 相 同 ， 则 称 这 两 个 二 次 函 数 为 “ 同 簇 二 次 函 数 ” ． （ 1） 请 写 出 两 个 为 “ 同 簇 二 次 函 数 ” 的 函 数 ； （ 2） 已 知 关 于 x 的 二 次 函 数 y 1=2x2-4mx+2m2+1 和 y2=ax2+bx+5， 其 中 y 1 的 图 象 经 过 点 A（ 1， 1）， 若 y 1+y2 与 y1 为 “ 同 簇 二 次 函 数 ”， 求 函 数 y2 的 表 达 式 ， 并 求 出 当 0≤ x≤ 3 时 ， y 2 的 最 大 值 ． 25．（2013•绵阳）我们知道，三角形的三条中线一定会交于一点，这一点就叫做三角形的 重心．重心有很多美妙的性质，如关于线段比．面积比就有一些“漂亮”结论，利用这些性质 可以解决三角形中的若干问题．请你利用重心的概念完成如下问题： （1）若 O 是△ABC 的重心（如图 1），连结 AO 并延长交 BC 于 D，证明： ； （2）若 AD 是△ABC 的一条中线（如图 2），O 是 AD 上一点，且满足 ，试判断 O 是△ABC 的重心吗？如果是，请证明；如果不是，请说明理由； （3）若 O 是△ABC 的重心，过 O 的一条直线分别与 AB、AC 相交于 G、H（均不与△ABC 的顶点重合）（如图 3），S 四边形 BCHG，S△AGH 分别表示四边形 BCHG 和△AGH 的面积， 试探究 的最大值． 3 a b c+ 2 3 AO AD = 2 3 AO AD = BCHG AGH S S 四边形 专题二 新定义型问题参考答案 三、中考典例剖析 考点一：规律题型中的新定义 例 1 解：A、 ∵ 2 有 3 个 ， ∴ 不 可 以 作 为 S 1， 故 选 项 错 误 ； B、 ∵ 2 有 3 个 ， ∴ 不 可 以 作 为 S 1， 故 选 项 错 误 ； C、 3 只 有 1 个 ， ∴ 不 可 以 作 为 S 1， 故 选 项 错 误 D、 符 合 定 义 的 一 种 变 换 ， 故 选 项 正 确 ． 故 选 ： D． 考点二：运算题型中的新定义 例 2 解：-1⊗ 2=2 2-（ -1） × 2=6， 6⊗ 3=3 2-6× 3=-9． 所 以 （ -1⊗ 2） ⊗ 3=-9． 故 答 案 为 -9． 考点三：探索题型中的新定义 例 3 解：如图， ∵到直线 l1 的距离是 1 的点在与直线 l1 平行且与 l1 的距离是 1 的两条平行线 a1、a2 上， 到直线 l2 的距离是 2 的点在与直线 l2 平行且与 l2 的距离是 2 的两条平行线 b1、b2 上， ∴“距离坐标”是（1，2）的点是 M1、M2、M3、M4，一共 4 个． 故选 C． 考点四：开放题型中的新定义 例 4 解：（ 1） 根 据 有 界 函 数 的 定 义 知 ， 函 数 y= （ x＞ 0） 不 是 有 界 函 数 ． y=x+1（ -4≤ x≤ 2） 是 有 界 函 数 ． 边 界 值 为 ： 2+1=3； （ 2） ∵ 函 数 y=-x+1 的 图 象 是 y 随 x 的 增 大 而 减 小 ， ∴ 当 x=a 时 ， y=-a+1=2， 则 a=-1 当 x=b 时 ， y=-b+1． 则 ， ∴ -1＜ b≤ 3； （ 3） 若 m＞ 1， 函 数 向 下 平 移 m 个 单 位 后 ， x=0 时 ， 函 数 值 小 于 -1， 此 时 函 数 的 边 界 t≥ 1， 与 题 意 不 符 ， 故 m≤ 1． 当 x=-1 时 ， y=1 即 过 点 （ -1， 1） 1 x 2 b 1 2 b a a 1 − ≤ − + ≤   − ＞ ＝ 当 x=0 时 ， y 最 小 =0， 即 过 点 （ 0， 0） ， 都 向 下 平 移 m 个 单 位 ， 则 （ -1， 1-m） 、 （ 0， -m） ≤ 1-m≤ 1 或 -1≤ -m≤ - ， ∴ 0≤ m≤ 或 ≤ m≤ 1． 考点五：阅读材料题型中的新定义 例 5 解：（ 1） ∵ P 0（ 2， -3） ， O 为 坐 标 原 点 ， ∴ d（ O， P 0） =|0-2|+|0-（ -3） |=5． 故 答 案 为 ： 5； （ 2） ∵ P（ a， -3） 到 直 线 y=x+1 的 直 角 距 离 为 6， ∴ 设 直 线 y=x+1 上 一 点 Q（ x， x+1） ， 则 d（ P， Q） =6， ∴ |a-x|+|-3-x-1|=6， 即 |a-x|+|x+4|=6， 当 a-x≥ 0， x≥ -4 时 ， 原 式 =a-x+x+4=6， 解 得 a=2； 当 a-x＜ 0， x＜ -4 时 ， 原 式 =x-a-x-4=6， 解 得 a=-10． 故 答 案 为 ： 2 或 -10． 四、中考真题演练 一、选择题 1．C 2．A 3．D 4．A 5．D 6．D 7．C 二、填空题 8. {-3， -2， 0， 1， 3， 5， 7} 9．２ 10．（ -3， 1） ， （ 0， 4） ； -1＜ a＜ 1 且 0＜ b＜ 2 11． 12． ， ：1， 13．137.5 14．30° 三、解答题 3 4 3 4 1 4 3 4 45 99 2 2 2 1 4 a − 15．解：∵m+n=mn 且 m，n 是正实数， ∴ +1=m，即 =m-1， ∴P（m，m-1）， 即“完美点”P 在直线 y=x-1 上， ∵点 A（0，5）在直线 y=-x+b 上， ∴b=5， ∴直线 AM：y=-x+5， ∵“完美点”B 在直线 AM 上， ∴由 解得 ， ∴B（3，2）， ∵一、三象限的角平分线 y=x 垂直于二、四象限的角平分线 y=-x，而直线 y=x-1 与直线 y=x 平行，直线 y=-x+5 与直线 y=-x 平行， ∴直线 AM 与直线 y=x-1 垂直， ∵点 B 是直线 y=x-1 与直线 AM 的交点， ∴垂足是点 B， ∵点 C 是“完美点”， ∴点 C 在直线 y=x-1 上， ∴△MBC 是直角三角形， ∵B（3，2），A（0，5）， ∴AB=3 ， ∵AM=4 ，∴BM= ， 又∵CM= ， ∴BC=1， m n m n y x 1 y x 5 ＝ ＝ −  − + x 3 y 2 ＝ ＝    2 2 2 3 ∴S△MBC= BM•BC= ． 16．解 ： 由 题 意 得 2x-（ 3-x） ＞ 0， 去 括 号 得 ： 2x-3+x＞ 0， 移 项 合 并 同 类 项 得 ： 3x＞ 3， 把 x 的 系 数 化 为 1 得 ： x＞ 1． 17．解 ： （ 1） 如 图 1 所 示 ： ∵ AB=AC， ∠ A=36° ， ∴ 当 AE=BE， 则 ∠ A=∠ ABE=36° ， 则 ∠ AEB=108° ， 则 ∠ EBC=36° ， ∴ 这 2 个 等 腰 三 角 形 的 顶 角 度 数 分 别 是 108 度 和 36 度 ； 故 答 案 为 ： 108， 36； （ 2） 如 图 2 所 示 ： （ 3） 如 图 3 所 示 ： 当 1 条 直 线 可 得 到 2 个 等 腰 三 角 形 ； 当 2 条 直 线 可 得 到 4 个 等 腰 三 角 形 ； 当 3 条 直 线 可 得 到 6 个 等 腰 三 角 形 ； … ∴ 在 △ ABC 中 画 n 条 线 段 ， 则 图 中 有 2n 个 等 腰 三 角 形 ， 其 中 有 n 个 黄 金 等 腰 三 角 形 ． 故 答 案 为 ： 2n， n． 18．解：（1）①如图 1 所示，过点 E 作⊙O 的切线设切点为 R， ∵⊙O 的半径为 1，∴RO=1， ∵EO=2， ∴∠OER=30°， 根据切线长定理得出⊙O 的左侧还有一个切点，使得组成的角等于 30°， ∴E 点是⊙O 的关联点， ∵D（ ， ），E（0，-2），F（2 ，0）， ∴OF＞EO，DO＜EO， ∴D 点一定是⊙O 的关联点，而在⊙O 上不可能找到两点使得组成的角度等于 60°， 故在点 D、E、F 中，⊙O 的关联点是 D，E； 故答案为：D，E； 1 2 2 2 1 2 1 2 3 ②由题意可知，若 P 要刚好是⊙C 的关联点， 需要点 P 到⊙C 的两条切线 PA 和 PB 之间所夹的角为 60°， 由图 2 可知∠APB=60°，则∠CPB=30°， 连接 BC，则 PC= =2BC=2r， ∴若 P 点为⊙C 的关联点，则需点 P 到圆心的距离 d 满足 0≤d≤2r； 由上述证明可知，考虑临界点位置的 P 点， 如图 3，点 P 到原点的距离 OP=2×1=2， 过点 O 作 l 轴的垂线 OH，垂足为 H，tan∠OGF= = ， ∴∠OGF=60°， ∴OH=OGsin60°= ； sin∠OPH= ， ∴∠OPH=60°， 可得点 P1 与点 G 重合， 过点 P2 作 P2M⊥x 轴于点 M， 可得∠P2OM=30°， ∴OM=OP2cos30°= ， 从而若点 P 为⊙O 的关联点，则 P 点必在线段 P1P2 上， sin BC CPB∠ 2 3 2 FO OG = 3 3 3 2 OH OP = 3 ∴0≤m≤ ； （2）若线段 EF 上的所有点都是某个圆的关联点，欲使这个圆的半径最小，则这个圆的圆 心应在线段 EF 的中点； 考虑临界情况，如图 4， 即恰好 E、F 点为⊙K 的关联时，则 KF=2KN= EF=2， 此时，r=1， 故若线段 EF 上的所有点都是某个圆的关联点，这个圆的半径 r 的取值范围为 r≥1． 19．解 ： （ 1） 相 同 点 ： ① 两 组 邻 边 分 别 相 等 ； ② 有 一 组 对 角 相 等 ； ③ 一 条 对 角 线 垂 直 平 分 另 一 条 对 角 线 ； ④ 一 条 对 角 线 平 分 一 组 对 角；⑤ 都 是 轴 对 称 图 形；⑥ 面 积 等 于 对 角 线 乘 积 的 一 半； 不 同 点 ： ① 菱 形 的 对 角 线 互 相 平 分 ， 筝 形 的 对 角 线 不 互 相 平 分 ； ② 菱 形 的 四 边 都 相 等 ， 筝 形 只 有 两 组 邻 边 分 别 相 等 ； ③ 菱 形 的 两 组 对 边 分 别 平 行 ， 筝 形 的 对 边 不 平 行 ； ④ 菱 形 的 两 组 对 角 分 别 相 等 ， 筝 形 只 有 一 组 对 角 相 等 ； ⑤ 菱 形 的 邻 角 互 补 ， 筝 形 的 邻 角 不 互 补 ； ⑥ 菱 形 的 既 是 轴 对 称 图 形 又 是 中 心 对 称 图 形 ，筝形 是 轴 对 称 图 形 不 是 中 心 对 称 图 形 ； （ 2） 如 图 所 示 ： ． 20． 解 ： （ 1） ∵ 点 P（ 1， 1） ， 3 1 2 ∴ 点 P 到 直 线 y=3x-2 的 距 离 为 ： d= =0， ∴ 点 P 在 直 线 y=3x-2 上 ； （ 2） 由 题 意 ， 得 ∵ y=2x-1 ∴ k=2， b=-1． ∵ P（ 2， -1） ， ∴ d= = ． ∴ 点 P（ 2， -1） 到 直 线 y=2x-1 的 距 离 为 ； （ 3） 在 直 线 y=-x+1 任 意 取 一 点 P， 当 x=0 时 ， y=1． ∴ P（ 0， 1） ． ∵ 直 线 y=-x+3， ∴ k=-1， b=3， ∴ d= = ， ∴ 两 平 行 线 之 间 的 距 离 为 ． 21． 解：（1）∵l∥k，BE⊥l， ∴∠BFC=∠BEA=90°， ∴∠ABE+∠BAE=90°， ∵四边形 ABCD 是正方形， ∴∠ABC=90°，AB=BC． ∴∠ABE+∠CBF=90°， ∴∠BAE=∠CBF， ∴△ABE≌△BCF， ∴AE=BF， ∵d1=d3=1，d2=2， ∴BE=3，AE=1， 在 直 角 △ABE 中 ， AB= ＝ ＝ ， 即正方形的边长是 ； （2）过 B 作 BE⊥l 于点 E，交 k 于点 2 | 3 1 1 2 | 1 3 × − − + ( ) 2 | 2 2 1 1 | 1 2 × − − − + 4 5 5 4 5 5 ( )2 | 0 1 3 | 2 1 1 − − + = + − 2 2 2 2BE AE+ 2 23 1+ 10 10 F． 则 BE=1，BF=3， ∵四边形 ABCD 是矩形， ∴∠ABC=90°， ∴∠ABE+∠FBC=90°， 又∵直角△ABE 中，∠ABE+∠EAB=90°， ∴∠FBC=∠EAB， ∴△AEB∽△BFC， 当 AB 是较短的边时，如图（a）， AB= BC，则 AE= BF= ， 在直角△ABE 中，AB= ； 当 AB 是长边时，如图（b）， 同理可得：BC= ； 故答案为： 或 ； （3）证明：如解答图 1，连接 AC， ∵四边形 ABCD 是菱形，且∠ADC=60°，∴AC=AD， ∵△AEF 是等边三角形， ∴AE=AF， ∵AE⊥k，∠AFD=90°， ∴∠AEC=∠AFD=90°， ∴直角△AEC≌直角△AFD， ∴EC=DF； （4）当 2＜DH＜4 时，BC∥DE．理由如下： 如图 2，当 2＜DH＜4 时，点 D 在线段 CM 上，连接 AM． ∵∠ABM=∠ACM=90°，AB=AC，AM=AM， ∴Rt△ABM≌Rt△ACM， ∴∠BAM=∠CAM， ∴AM⊥BC， 又∵AD=AE，AB=AC， ∴Rt△ABE≌Rt△ACD， ∴∠BAE=∠CAD， ∴∠EAM=∠DAM， 1 2 1 2 3 2 23 131 2 2  + =   37 2 13 2 37 2 ∴AM⊥ED．∴BC∥DE． 22．解：（1）反比例函数 y= 是闭区间[1，2014]上的“闭函数”，理由如下： 反比例函数 y= 在第一象限，y 随 x 的增大而减小， 当 x=1 时，y=2014； 当 x=2014 时，y=1， 所以，当 1≤x≤2014 时，有 1≤y≤2014，符合闭函数的定义，故 反比例函数 y= 是闭区间[1，2014]上的“闭函数”； （2）分两种情况：k＞0 或 k＜0． ①当 k＞0 时，一次函数 y=kx+b（k≠0）的图象是 y 随 x 的增大而增大，故根据“闭函数” 的定义知， ， 解得 ． ∴此函数的解析式是 y=x； ②当 k＜0 时，一次函数 y=kx+b（k≠0）的图象是 y 随 x 的增大而减小，故根据“闭函数” 的定义知， ， 解得 ． ∴此函数的解析式是 y=-x+m+n； （3）∵y= x2-2x= (x2-4x+4)-2= (x-2)2-2， ∴该二次函数的图象开口方向向上，最小值是-2，且当 x＜2 时，y 随 x 的增大而减小；当 x ＞2 时，y 随 x 的增大而增大． ①当 c＜2＜d 时，此时二次函数 y= x2-2x 的最小值是-2=c，根据“闭函数”的定义知， d= c2-2c 或 d= d2-2d； Ⅰ）当 d= c2-2c 时，由于 d= ×（-2）2-2×（-2）=6＞2，符合题意； 2014 x 2014 x 2014 x km b m kn b n ＝ ＝ +  + k 1 b 0 ＝ ＝    km b n kn b m ＝ ＝ +  + k 1 b m n ＝ ＝ −  + 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 Ⅱ）当 d= d2-2d 时，解得 d=0 或 6， 由于 d＞2， 所以 d=6； ②当 c≥2 时，此二次函数 y 随 x 的增大而增大，则根据“闭函数”的定义知， ， 解得， ， ∵c＜d， ∴ 不合题意，舍去． 综上所述，c，d 的值分别为-2，6． 23．解 ： （ 1） 在 Rt△ ABC 中 ， tan∠ ABC= ， 则 BC= ， 同 理 ， B1C= ， ∵ B1B=B1C-BC， ∴ ， AC=30， 解 得 ： AC≈ 39（ 米 ） ； （ 2） ∵ B 1B=AB， ∴ ∠ B1=∠ B 1AB= ∠ ABC=15° ， 设 B1B=AB=x， 在 Rt△ ABC 中 ， ∠ ABC=30° ， ∴ AC= AB= x， BC= x， ∴ B1C=x+ x， ∴ tan15° = ； 1 2 2 2 1 22 1 22 c c c d d d  − =  − = 6 6 c d =  = 6 6 c d =  = AC BC 3tan30 AC AC=° tan 22 AC ° 3 300.40 AC AC− = 1 2 1 2 1 2 3 2 3 2 1 1 12 2 3 3 2 3 2 xAC B C x = = = − ++ （ 3） 如 答 图 3 所 示 ， 图 中 三 角 形 依 次 是 含 有 7.5° 角 、 15° 角 和 30° 角 的 直 角 三 角 形 ． 设 AC=a， 则 AB=2a， BC= ． ∴ B1B=AB=2a， ∴ B1C=2a+ a=（ 2+ ） a． 在 Rt△ AB 1C 中 ， 由 勾 股 定 理 得 ： AB1= ＝ ， ∴ B2B1=AB1=2 ， ∴ B2C=B2B1+B1C= ∴ tan7.5° =tan∠ AB 2C=tan = , ∴ tan7.5° = ． 24. 解 ： （ 1） 设 顶 点 为 （ h， k） 的 二 次 函 数 的 关 系 式 为 y=a（ x-h） 2+k， 当 a=2， h=3， k=4 时 ， 二 次 函 数 的 关 系 式 为 y=2（ x-3） 2+4． ∵ 2＞ 0， ∴ 该 二 次 函 数 图 象 的 开 口 向 上 ． 当 a=3， h=3， k=4 时 ， 二 次 函 数 的 关 系 式 为 y=3（ x-3） 2+4． ∵ 3＞ 0， ∴ 该 二 次 函 数 图 象 的 开 口 向 上 ． ∵ 两 个 函 数 y=2（ x-3） 2+4 与 y=3（ x-3） 2+4 顶 点 相 同 ， 开 口 都 向 上 ， ∴ 两 个 函 数 y=2（ x-3） 2+4 与 y=3（ x-3） 2+4 是 “ 同 簇 二 次 函 数 ” ． ∴ 符 合 要 求 的 两 个 “ 同 簇 二 次 函 数 ” 可 以 为 ： y=2 （ x-3 ） 2+4 与 y=3 （ x-3 ） 2+4． （ 2） ∵ y 1 的 图 象 经 过 点 A（ 1， 1） ， ∴ 2× 12-4× m× 1+2m2+1=1． 整 理 得 ： m2-2m+1=0． 解 得 ： m1=m2=1． 3tan30 AC a=° 3 3 2 2 1B C AC+ ( )2 2 22 3 2 2 3a a a+ + = + 2 2 3a+ ( )2 2 3 2 3a a+ + + 2AB C∠ ( )2 2 2 3 2 3 AC a B C a a = + + + 1 2 2 3 2 3+ + + ∴ y1=2x2-4x+3 =2（ x-1） 2+1． ∴ y1+y2=2x2-4x+3+ax2+bx+5 =（ a+2） x 2+（ b-4） x+8 ∵ y1+y2 与 y1 为 “ 同 簇 二 次 函 数 ” ， ∴ y1+y2=（ a+2） （ x-1） 2+1 =（ a+2） x 2-2（ a+2） x+（ a+2） +1． 其 中 a+2＞ 0， 即 a＞ -2． ∴ ． 解 得 ： ． ∴ 函 数 y2 的 表 达 式 为 ： y2=5x2-10x+5． ∴ y2=5x2-10x+5 =5（ x-1） 2． ∴ 函 数 y2 的 图 象 的 对 称 轴 为 x=1． ∵ 5＞ 0， ∴ 函 数 y2 的 图 象 开 口 向 上 ． ① 当 0≤ x≤ 1 时 ， ∵ 函 数 y2 的 图 象 开 口 向 上 ， ∴ y2 随 x 的 增 大 而 减 小 ． ∴ 当 x=0 时 ， y2 取 最 大 值 ， 最 大 值 为 5（ 0-1） 2=5． ② 当 1＜ x≤ 3 时 ， ∵ 函 数 y2 的 图 象 开 口 向 上 ， ∴ y2 随 x 的 增 大 而 增 大 ． ∴ 当 x=3 时 ， y2 取 最 大 值 ， 最 大 值 为 5（ 3-1） 2=20． 综 上 所 述 ： 当 0≤ x≤ 3 时 ， y 2 的 最 大 值 为 20． 25． 解 ： （1）证明：如答图 1 所示，连接 CO 并延长，交 AB 于点 E． ∵点 O 是△ABC 的重心，∴CE 是中线，点 E 是 AB 的中点． ∴DE 是中位线， b 4 2(a 2) 8 (a 2) 1 − − +  + + ＝ ＝ a 5 b 10   − ＝ ＝ ∴DE∥AC，且 DE= AC． ∵DE∥AC， ∴△AOC∽△DOE， ∴ =2， ∵AD=AO+OD， ∴ = ． （2）答：点 O 是△ABC 的重心． 证明：如答图 2，作△ABC 的中线 CE，与 AD 交于点 Q，则点 Q 为△ABC 的重心． 由（1）可知， = ， 而 = ， ∴点 Q 与点 O 重合（是同一个点）， ∴点 O 是△ABC 的重心． （3）如答图 3 所示，连接 DG． 设 S△GOD=S，由（1）知 = ，即 OA=2OD， ∴S△AOG=2S，S△AGD=S△GOD+S△AGO=3S． 为简便起见，不妨设 AG=1，BG=x，则 S△BGD=3xS． ∴S△ABD=S△AGD+S△BGD=3S+3xS=（3x+3）S， ∴S△ABC=2S△ABD=（6x+6）S． 1 2 AO AC OD DE = AO AD 2 3 AO AD 2 3 AO AD 2 3 AO AD 2 3 设 OH=k•OG，由 S△AGO=2S，得 S△AOH=2kS， ∴S△AGH=S△AGO+S△AOH=（2k+2）S． ∴S 四边形 BCHG=S△ABC-S△AGH=（6x+6）S-（2k+2）S=（6x-2k+4）S． ∴ = = ① 如答图 3，过点 O 作 OF∥BC 交 AC 于点 F，过点 G 作 GE∥BC 交 AC 于点 E，则 OF∥GE． ∵OF∥BC， ∴ ， ∴OF= CD= BC； ∵GE∥BC， ∴ ， ∴GE= ； ∴ = ， ∴ = ． ∵OF∥GE， ∴ ， ∴ ， ∴k= ，代入①式得： = =-x2+x+1=-（x- ）2+ ， ∴当 x= 时， 有最大值，最大值为 ． BCHG AGH S S 四边形 (6 - 2 4) (2 2) x k S k S + + 3 - 2 1 x k k + + 2 3 OF AO CD AD = = 2 3 1 3 1 1 GE AG BC AB x = = + 1 BC x + 1 3 1 BCOF BCGE x = + 1 3 x + 1 3 ( 1) OF x GE OF x +=− − + 1 2 x x + − OH OF GH GE = 1 - 2- OH OF x OG GE OF x += = 1 2- x x + BCHG AGH S S 四边形 13 - 23 - 2 2- 11 12- xxx k x xk x + ++ = ++ + 1 2 5 4 1 2 BCHG AGH S S 四边形 5 4