中考复习之多动点综合题中等腰三角形的专题研究 15页

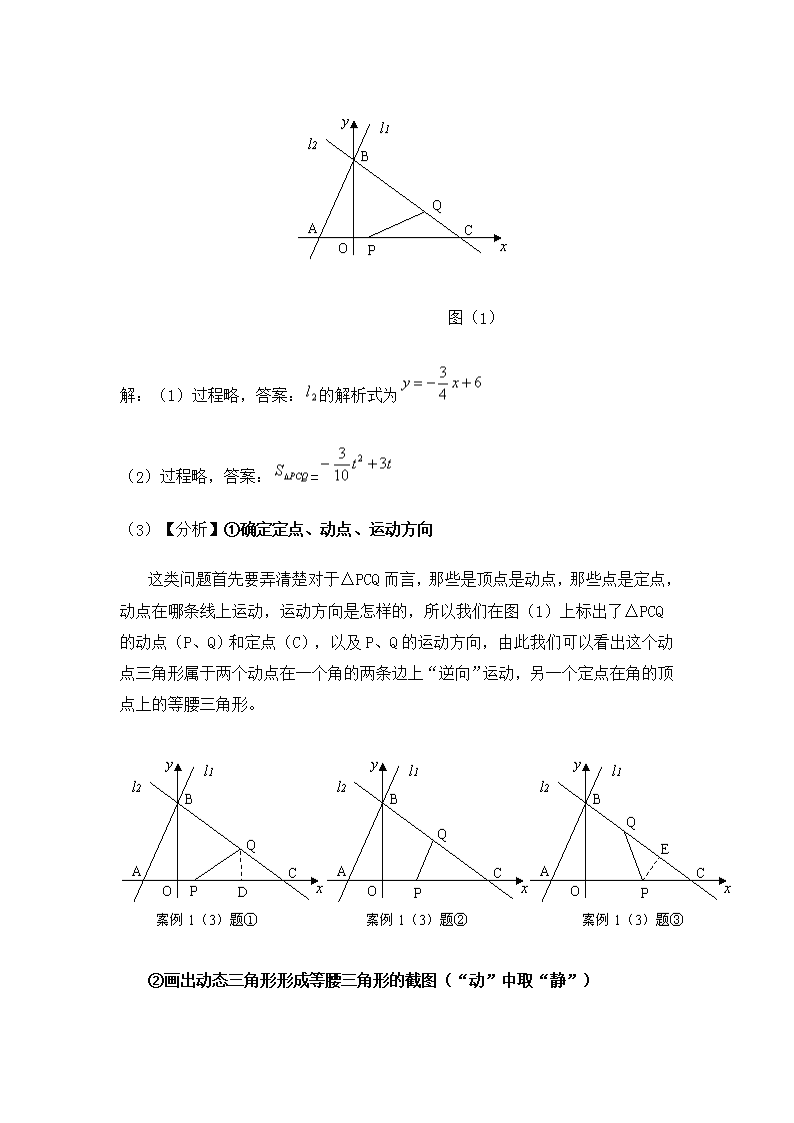
多动点综合题中等腰三角形的专题研究 动态几何题是各地中考“压轴题”的亮点之一。这类题型的信息量大，经常把数与方程、函数与几何、函数与解直角三角形、函数与面积等联系在一起。解题时要用运动和变化的眼光去观察、思考、研究问题，把握图形运动、变化的全过程，综合运用函数、方程、分类讨论、数形结合等数学思想去解决问题。‎ 如果把中考数学的压轴题比喻成皇后头上的皇冠的话，压轴题中的压轴问题就是皇后皇冠上的一颗最璀璨夺目的明珠。近几年的多个地区中考试题压轴题的最后一问，都是以多动点的几何背景为载体，探究等腰三角形的问题。本文通过对几何背景综合题中等腰三角形的专题研究，寻找解题规律，了解、掌握在几何背景综合题中等腰三角形的常见解法，并感悟解几何背景综合题的一般思考方法，以供九年级师生复习参考之用。‎ 一、两个动点在一个角的两边上“逆向”运动，另一个定点在角的顶点上的等腰三角形 ‎【案例1】（2008山西）如图（1），已知直线的解析式为，直线与x轴、y轴分别相交于A、B两点，直线经过B、C两点，点C的坐标为（8，0），又已知点P在x轴上从点A向点C移动，点Q在直线从点C向点B移动。点P、Q同时出发，且移动的速度都为每秒1个单位长度，设移动时间为t秒（）。‎ ‎（1）求直线的解析式。‎ ‎（2）设△PCQ的面积为S，请求出S关于t的函数关系式。‎ ‎（3）试探究：当t为何值时，△PCQ为等腰三角形？‎ ‎　　　　　　　　　　　‎ ‎          　　　　　　　　　　　图（1）‎ 解：（1）过程略，答案：的解析式为 ‎（2）过程略，答案：=‎ ‎（3）【分析】①确定定点、动点、运动方向 这类问题首先要弄清楚对于△PCQ而言，那些是顶点是动点，那些点是定点，动点在哪条线上运动，运动方向是怎样的，所以我们在图（1）上标出了△PCQ的动点（P、Q）和定点（C），以及P、Q的运动方向，由此我们可以看出这个动点三角形属于两个动点在一个角的两条边上“逆向”运动，另一个定点在角的顶点上的等腰三角形。‎ ‎②画出动态三角形形成等腰三角形的截图（“动”中取“静”）‎ 按照运动时间先后的顺序，往往存在三种情况，这里体现了分类讨论的思想，⊿PCQ的三边两两分别相等，如图①QP=QC，②CP=CQ，③PC=PQ，这个过程需要读者在备用图中试画。只有画出来才能求出来，所以这一步在整个问题中是相当关键的，注意不要重复和遗漏。‎ ‎③在函数与数形结合思想的基础上，利用勾股定理、锐角三角函数与相似关系建立方程 ‎     根据题意我们可知，很多和问题有关的边长都可以用时间的式子表示出来，PC=，CQ=，建立等式模型时，我们往往要运用勾股定理、锐角三角函数与相似，但利用以上的方法所需的基本图形是直角三角形，所以我们这里要把一个等腰三角形转化为两个全等的直角三角形。‎ ‎     如图①，当QC=QP，过Q作QD⊥轴于D，D点为PC中点，则CD=PC=，图形中可确定三边的Rt⊿BOC，恰好这个直角三角形与我们把等腰三角形QPC分割出来的Rt⊿QDC公共∠BCO，根据“A”型相似或平行相似，则⊿QDC∽⊿BOC，，即，解得 ‎    如图②，当CP=CQ时，这时CP与CQ正好也在∠BCO的两边上，，解得 ‎    如图③，当PC=PQ时，过P作PE⊥于E，则CE=CQ=，这时分割出的Rt⊿PEC与已知的Rt⊿BOC仍然公共∠BCO，并形成斜“A”型相似，则⊿PEC∽⊿BOC，‎ ‎，即，解得，‎ 综上所述，当，或5，或时，（都满足），⊿PCQ为等腰三角形 ‎【总结】以上题目是动点和函数思想相结合以几何图形为背景，以动点为元素,构造动态型几何问题。解此类题目，应从相关图形的性质和数量关系分类讨论来解决。此类问题较多地关注学生对图形性质的理解,用动态的观点去看待一般函数和图形结合的问题,具有较强的综合性。‎ ‎【练习】（2009济南）如图（2），在梯形中，∥,,,,‎ ‎　　　　　　图（2）‎ ‎ ‎ 动点从点出发沿线段以每秒2个单位长度的速度向终点运动；动点同时从点出发沿线段以每秒1个单位长度的速度向终点运动．设运动的时间为秒．‎ ‎（1）求的长。（过程略，）‎ ‎（2）当∥时，求的值。(过程略，)‎ ‎（3）试探究：为何值时，为等腰三角形。‎ 解：（3）【分析】①确定定点、动点、运动方向（请读者自行在图（2）中完成）‎ ‎②画出动态三角形形成等腰三角形的截图（请读者自行在练习图①②③中完成）‎ ‎③在函数与数形结合思想的基础上，利用勾股定理、锐角三角函数与相似关系建立方程 点拨：此问所需要确定三边的直角三角形，目标就锁定到梯形分割出右边的这个直角三角形，这个三边都可以求出的直角三角形还与动态公共∠C，可利用案例一的讨论方法求出相应的时间，注意这题中M、N两个动点的速度不一样了，此问答案为当、或时，为等腰三角形，过程请读者自行完成。‎ ‎【案例2】（2009仙桃）如图（3），直角梯形ABCD中，AD∥BC，∠ABC＝90°，已知AD＝AB＝3，BC＝4，动点P从B点出发，沿线段BC向点C作匀速运动；动点Q从点D 出发，沿线段DA向点A作匀速运动．过Q点垂直于AD的射线交AC于点M，交BC于点N．P、Q两点同时出发，速度都为每秒1个单位长度．当Q点运动到A点，P、Q两点同时停止运动．设点Q运动的时间为t秒．‎ ‎(1)求NC，MC的长(用t的代数式表示)；（过程略，）‎ ‎(2)当为何值时，四边形PCDQ构成平行四边形？(过程略，)‎ ‎(3)是否存在某一时刻，使射线QN恰好将的面积和周长同时平分？若存在，求出此时的值；若不存在，请说明理由；（过程略，不存在）‎ ‎(4)探究：为何值时，为等腰三角形？‎ ‎　　　　　　　　　　　　　　‎ 解：（3）【分析】①确定定点、动点、运动方向由题意可知Q、M、N三点在同一条直线上，M、N随着Q点的移动而移动②画出动态三角形形成等腰三角形的截图画出动态的三种情况，如图①、②、③‎ ‎③在函数与数形结合思想的基础上，利用勾股定理、锐角三角函数与相似关系建立方程 此问所用到的方法和案例1有所不同，这时只知道P、Q两个动点的速度，所以动态的CM边不能直接用的式子表示出来，此题的PC=，CN=，接下来就要围绕者PC，CN两边来建立方程。‎ 如图①，当MP=MC，而MN⊥PC， 则N点为PC中点，有PC=2NC，有 解得：=‎ 如图②，当CM=CP时，CM=CP=，CN=，而由图中可以知Rt⊿MNC与Rt⊿ABC公共∠ACB，根据“A”型相似或平行相似，，，解得：‎ 如图③，当PM=PC时，PM=PC=，则PN=CN－PC=， Rt⊿MNC与Rt⊿ABC公共∠ACB，本应该利用这种平行相似关系建立方程，可Rt⊿MNC只有一边CN可以由表示出来，只有利用其它方法建立等式，由上可知Rt⊿MNP中的PM、PN都可以用表示出来，只差最后一边MN没有用表示出来，这里刚好可以利用Rt⊿MNC与Rt⊿ABC相似把MN也用表示出来，,,则MN=，最后我们利用在Rt⊿MNP中存在勾股定理，完成建立方程的步骤，,‎ ‎，解得（-1舍）‎ 综上所述当、或时，为等腰三角形 二、两动点在两条平行线上同向运动，另一个动点在另一边上运动的等腰三角形问题 ‎【案例3】（2008温州）如图（4），在Rt△ABC中，∠A＝90?，AB＝6，AC＝8，D，E分别是边AB，AC的中点，点P从点D出发沿DE方向运动，过点P作PQ⊥BC于Q，过点Q作QR∥BA交AC于R，当点Q与点C重合时，点P停止运动．设BQ＝x，QR＝y．‎ ‎（1）求点D到BC的距离DH的长；(过程略，)‎ ‎（2）求y关于x的函数关系式（不要求写出自变量的取值范围，过程略，）；‎ ‎（3）是否存在点P，使△PQR为等腰三角形？若存在，请求出所有满足要求的x的值；若不存在，请说明理由．‎ ‎　　　　　　　　　　　　　　　　　　‎ 解：（3）【分析】①确定定点、动点、运动方向由题意可知，点Q随点P向右移动而向右平行移动，而点R又随Q的移动而移动。②画出动态三角形形成等腰三角形的截图画出动态的三种情况，如图①、②、③‎ ‎　　‎ ‎　　案例3（3）图①　　　　　案例3（3）图②　　　　　　案例3（3）图③‎ ‎③在函数与数形结合思想的基础上，利用勾股定理、锐角三角函数与相似关系建立方程 根据题意我们可知，，PQ=，BQ＝x，RQ=，建立等式模型时，和案例1相同，我们这里要把一个等腰三角形转化为两个全等的直角三角形。‎ ‎     如图①，当PQ=PR，过P作PM⊥RQ于M，M点为RQ中点，则QM=RQ=‎ ‎=，由题意可知∠1+∠2=90°，∠C+∠B=90°，∠2=∠B，则∠1=∠C，即Rt⊿QMP∽Rt⊿CAB，，即，解得 ‎    如图②，当QP=QR时，=，解得 如图③，当RP=RQ时，过R作RN⊥PQ于N，则NQ=PQ=，∠NQR+∠RQC=‎ ‎90°，∠RQC +∠C=90°,则∠NQR=∠C，则Rt⊿QNR∽Rt⊿CAB，，即，解得，‎ 综上所述，当为，或6，或时，⊿PQR为等腰三角形。‎ ‎ ‎ ‎【练习】（2009江西）如图（5），在等腰梯形中，，是的中点，过点作交于点．，.‎ ‎（1）求点到的距离；(过程略，到的距离为)‎ ‎（2）点为线段上的一个动点，过作交于点，过作交折线于点，连结，设.‎ ‎①当点在线段上时，如图（6），的形状是否发生改变？若不变，求出的周长；若改变，请说明理由；（过程略，的周长=）‎ ‎②当点在线段上时，如图（7），是否存在点，使为等腰三角形？若存在，请求出所有满足要求的的值；若不存在，请说明理由.‎ 解：（3）【分析】①确定定点、动点、运动方向（请读者自行在图（7）中完成）‎ ‎②画出动态三角形形成等腰三角形的截图（请读者自行在练习图①②③中完成）‎ ‎③在函数与数形结合思想的基础上，利用勾股定理、锐角三角函数与相似关系建立方程 点拨：当点N在线段DC上运动时，⊿PMN的形状发生改变，但⊿MNC恒为等边三角形。过E作EG⊥BC于G，PM=EG=，GM=EP=，MN=NC=MC=5-，此问用到的方法与案例3类似，只不过这题∠B的度数更为特殊，由等腰三角形分解为直角三角形就为30°的直角三角形，所以用锐角三角函数比相似更容易建立方程，此问答案为当、或时，⊿PMN为等腰三角形，过程请读者自行完成。‎ 三、两动点在同一直线上运动，另一动点在另一边上运动的等腰三角形问题 ‎【案例4】（2009怀化）如图（8），在直角梯形OABC中， OA∥CB，A、B两点的坐标分别为A（15，0），B（10，12），动点P、Q分别从O、B两点出发，点 P以每秒2个单位的速度沿OA向终点A运动，点Q以每秒1个单位的速度沿BC向C运动，当点P停止运动时，点Q也同时停止运动．线段OB、PQ相交于点D，过点D作DE∥OA，交AB于点E，射线QE交轴于点F．设动点P、Q运动时间为t（单位：秒）．‎ ‎（1）当t为何值时，四边形PABQ是等腰梯形，请写出推理过程；（过程略，t =）‎ ‎（2）当t=2秒时，求梯形OFBC的面积；（过程略，S=174）‎ ‎（3）当t为何值时，△PQF是等腰三角形？请写出推理过程．‎ ‎　　　　　　　　　　　　　　　　　‎ 解：（3）【分析】①确定定点、动点、运动方向点P、F同向向x轴右移动，点Q在与x轴平行的BC上向左移动②画出动态三角形形成等腰三角形的截图③在函数与数形结合思想的基础上，利用勾股定理、锐角三角函数与相似关系建立方程 点拨：此题由于动态△PQF的三边任何时候都可以表示出来，所以分析②可以忽略，直接把三边表示出来（表示三边的过程用到了相似与勾股定理），令其两两分别相等建立方程。由题意可知QB=t，OP=2t，可推到出AF=2t，进而PF=15-2t+2t=15，‎ QP==，‎ QF==‎ ‎①当PQ=PF时，则=15，解得或 ‎②当QP=QF时，则=，解得 ‎③当FQ=FP时，则=15，解得或（舍）‎ 综上所述，当，，，时，△PQF是等腰三角形．‎ ‎【拓展】（2009江苏）如图（9-1），已知射线DE与轴和轴分别交于点和点．动点从点出发，以1个单位长度/秒的速度沿轴向左作匀速运动，与此同时，动点P从点D出发，也以1个单位长度/秒的速度沿射线DE的方向作匀速运动．设运动时间为秒．‎ ‎（1）请用含的代数式分别表示出点C与点P的坐标；（答案：，）‎ ‎（2）以点C为圆心、个单位长度为半径的与轴交于A、B两点（点A在点B的左侧），连接PA、PB．‎ ‎①当与射线DE有公共点时，求的取值范围；‎ ‎（答案：）‎ ‎②当为等腰三角形时，求的值．‎ ‎　　　　　　　　　　　　　　　　　‎ 解：（2-2）【分析】①确定定点、动点、运动方向A、B同向向x轴左移动，P点由点D向点B运动②画出动态三角形形成等腰三角形的截图③在函数与数形结合思想的基础上，利用勾股定理、锐角三角函数与相似关系建立方程 点拨：此题由于动态△PAB的三边任何时候都可以表示出来，所以分析②可以忽略，直接把三边表示出来（表示三边的过程用到了相似与勾股定理），令其两两分别相等建立方程。‎ ‎　　　　　　　　　　　　　　　　‎ 如图（9-2）由题意可知MC=t，BC=CA=，则MB=BC=CA=，进而AB=t，OA=，OB=,又PD=t，由相似可知PQ=，QD=，OQ=QP===QF==‎ 此问的答案为当，，，时，△PAB是等腰三角形，过程请读者自行完成。‎ 新课程实施以来，以动点几何为背景的压轴题，以等腰三角形为重要考点，是近年来中考压轴题中的一种重要题型。这类试题将代数和几何的众多知识有效整合，能有效考查学生分析新问题和解决新问题的能力，将解等腰三角形的所涉及到的分类思想，数形结合、化归、方程思想(根据勾股定理，相似，锐角三角函数列方程)体现得淋漓尽致。此题型属初高中衔接点，它对学生综合能力要求高，绝对难度大，很具有区分度。但这类新问题对培养学生的思维品质和各种数学能力都有很大的促进功能，对提高学生综合运用知识解决问题的能力有极大的帮助。解这类题不是一堂两堂课，一个专题就可以解决，它要求我们在平时教学中能渗透运动理念，用运动的眼光看问题，掌握好四个环节：渗透—变换—量化—训练，进行科学的施教。‎