一次函数中考真题精炼绝对有价值附答案DOC 52页

一次函数中考真题精炼 一、选择题 ‎1. （ 安徽芜湖，4，4分）函数中，自变量的取值范围是 ( ). ‎ A. B. C. D. ‎ ‎【答案】A ‎2. （ 安徽芜湖，7，4分）已知直线经过点和，则的值为（ ）. ‎ A． B． C． D． ‎ ‎【答案】B ‎3. （ 广东广州市，9，3分）当实数x的取值使得有意义时，函数y=4x+1中y的取值范围是（ ）．‎ A．y≥－7 B．y≥‎9 ‎ C．y＞9 D．y≤9‎ ‎【答案】B ‎4. （ 山东滨州，6，3分）关于一次函数y=－x+1的图像，下列所画正确的是( )‎ ‎【答案】C ‎5. （ 重庆江津， 4，4分）直线y=x－1的图像经过象限是( )‎ A.第一、二、三象限 B.第一、二、四象限 C.第二、三、四象限 D.第一、三、四象限 ‎【答案】D ‎6. 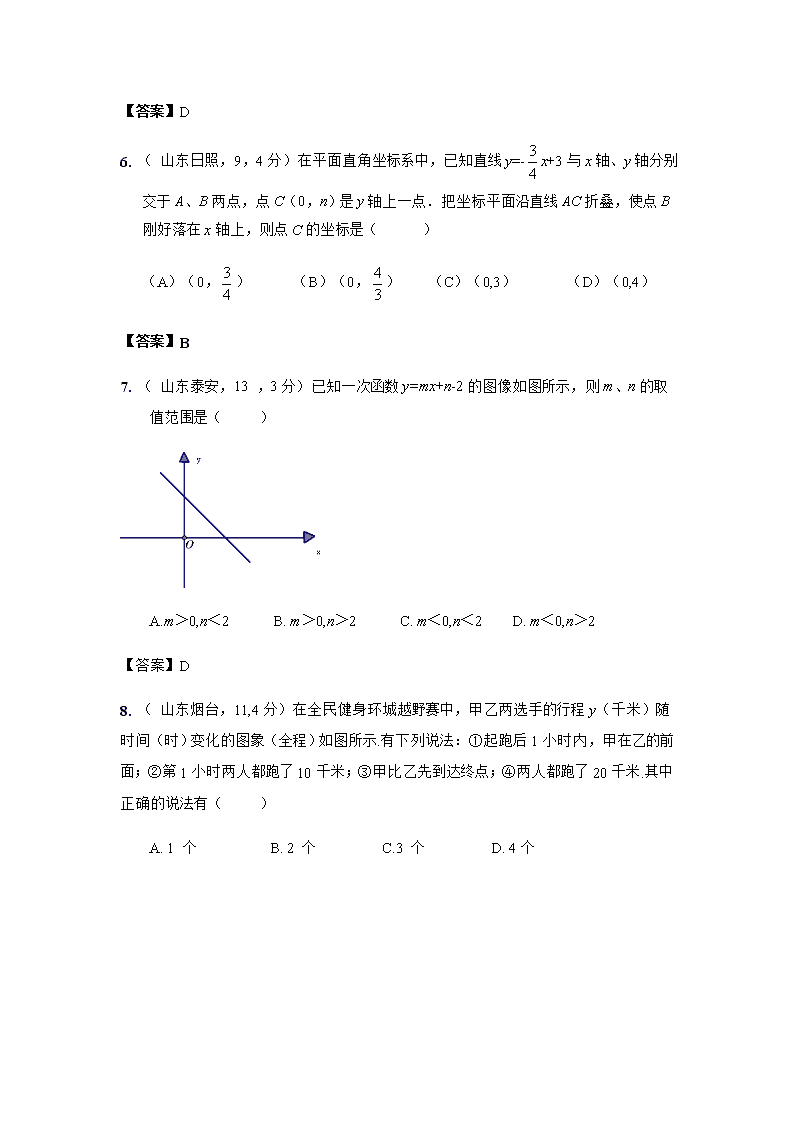（ 山东日照，9，4分）在平面直角坐标系中，已知直线y=-x+3与x轴、y轴分别交于A、B两点，点C（0，n）是y轴上一点．把坐标平面沿直线AC折叠，使点B刚好落在x轴上，则点C的坐标是（ ）‎ ‎（A）（0，） （B）（0，） （C）（0,3） （D）（0,4）‎ ‎【答案】B ‎7. （ 山东泰安，13 ，3分）已知一次函数y=mx+n-2的图像如图所示，则m、n的取值范围是（ ）‎ A.m＞0,n＜2 B. m＞0,n＞‎2 C. m＜0,n＜2 D. m＜0,n＞2‎ ‎【答案】D ‎ ‎8. （ 山东烟台，11,4分）在全民健身环城越野赛中，甲乙两选手的行程y（千米）随时间（时）变化的图象（全程）如图所示.有下列说法：①起跑后1小时内，甲在乙的前面；②第1小时两人都跑了10千米；③甲比乙先到达终点；④两人都跑了20千米.其中正确的说法有（ ）‎ A. 1 个 B. 2 个 C.3 个 D. 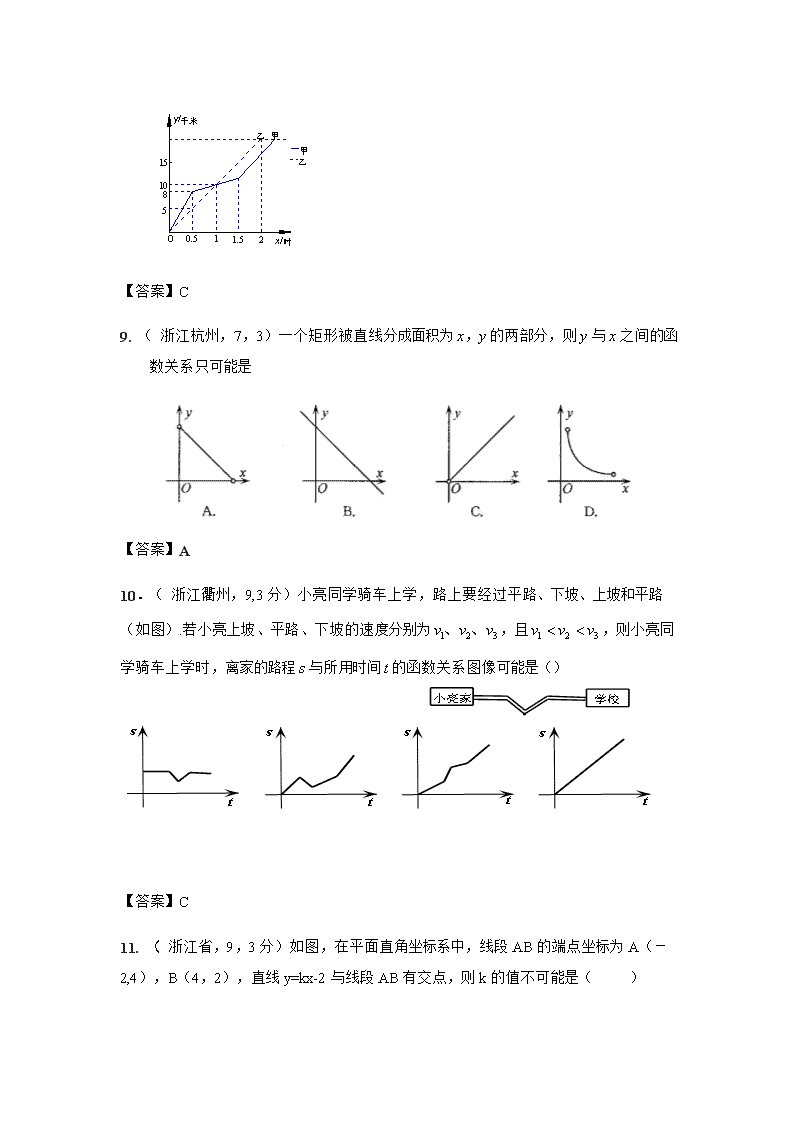4个 ‎【答案】C ‎9. （ 浙江杭州，7，3）一个矩形被直线分成面积为x，y的两部分，则y与x之间的函数关系只可能是 ‎【答案】A ‎10．（ 浙江衢州，9,3分）小亮同学骑车上学，路上要经过平路、下坡、上坡和平路（如图）.若小亮上坡、平路、下坡的速度分别为，且，则小亮同学骑车上学时，离家的路程与所用时间的函数关系图像可能是（）‎ ‎【答案】C ‎11. （ 浙江省，9，3分）如图，在平面直角坐标系中，线段AB的端点坐标为A（－2,4），B（4，2），直线y=kx-2与线段AB有交点，则k的值不可能是（ ）‎ A.-5 B.‎-2 C.3 D. 5 ‎ ‎【答案】B ‎12. （ 台湾台北，9）图(三)的坐标平面上，有一条通过点(－3,－2)的直线L。若四点(－2 , a)、(0 , b)、(c , 0)、(d ,－1)在L上，则下列数值的判断，何者正确？‎ A．a＝3 　　　B。b＞－‎2 　 ‎ C。c＜－3 　　　D 。d＝2‎ ‎【答案】C ‎13. （ 台湾全区，1）坐标平面上，若点(3, b)在方程式的图形上，则b值为何？‎ A．－1 B． ‎2 C．3 D． 9‎ ‎【答案】A ‎14. （ 江西，5，3分）已知一次函数y=x+b的图像经过一、二、三象限，则b的值可以是（ ）.‎ A.-2 B.‎-1 C.0 D.2‎ ‎【答案】D ‎15. （ 江西，8，3分）时钟在正常运行时，分针每分钟转动6，时针每分钟转动0.5.在运行过程中，时针与分针的夹角会随着时间的变化而变化.设时针与分针的夹角为y ‎（度），运行时间为t（分），当时间从12：00开始到12：30止，y与t之间的函数图像是（ ）.‎ ‎【答案】C ‎17. （ 四川成都，3,3分）在函数自变量的取值范围是 A ‎(A) (B) (C) (D) ‎ ‎【答案】A ‎18. （ 湖南常德，16，3分）设min｛x,y｝表示x,y两个数中的最小值，例如min｛0,2｝=0，min｛12,8｝=8，则关于x的函数y可以表示为（ ）‎ ‎ A. B. ‎ ‎ C. y =2x D. y=x＋2‎ ‎【答案】A ‎19. （ 江苏苏州，10,3分）如图，已知A点坐标为（5,0），直线y=x＋b（b>0）与y轴交于点B，连接AB，∠α=75°，则b的值为 A.3 B. C.4 D.‎ ‎【答案】B ‎20．（ 广东株洲，7，3分）根据生物学研究结果，青春期男女生身高增长速度呈现如下图规律，由图可以判断，下列说法错误的是：（ ）‎ ‎ A．男生在13岁时身高增长速度最快 B．女生在10岁以后身高增长速度放慢 ‎ C．11岁时男女生身高增长速度基本相同 D．女生身高增长的速度总比男生慢 ‎【答案】D ‎21. （ 山东枣庄，10，3分）如图所示，函数和的图象相交于（－1，1），（2，2）两点．当时，x的取值范围是（ ）‎ ‎（－1，1）‎ ‎（2，2）‎ x y O A．x＜－1 B．—1＜x＜‎2 ‎‎ C．x＞2 　　D． x＜－1或x＞2 ‎ ‎【答案】D ‎22. （ 江西南昌，5，3分）已知一次函数y=x+b的图像经过一、二、三象限，则b的值可以是（ ）.‎ A.-2 B.‎-1 C.0 D.2‎ ‎【答案】D ‎23. （ 湖南怀化，7，3分）在平面直角坐标系中，把直线y=x向左平移一个单位长度后，其直线解析式为 ‎ A．y=x+1 B.y=x‎-1 C.y=x D. y=x-2‎ ‎【答案】B ‎24. （ 四川绵阳4，3）使函数y=有意义的自变量x的取值范围是 A.x≤ B.x≠ C.x≥ D.x＜ ‎【答案】A ‎25. （ 四川乐山3，3分）下列函数中，自变量x的取值范围为x＜1的是 ‎ A． B． C． D．‎ ‎【答案】 D ‎26. （ 四川乐山8，3分）已知一次函数的图象过第一、二、四象限，且与x轴交于点（2，0），则关于x的不等式的解集为 ‎ A．x<－1 B．x> ‎-1 C． x>1 D．x<1‎ ‎【答案】A ‎27. （ 安徽芜湖，4,4分）函数中，自变量的取值范围是 ( ). ‎ A. B. C. D. ‎ ‎【答案】A ‎28. （ 安徽芜湖，7,4分）已知直线经过点和，则的值为（ ）. ‎ A． B． C． D． ‎ ‎【答案】B ‎29. （ 湖北武汉市，2，3分）函数 中自变量x的取值范围是 ‎     A．x ≥ 0．  B．x ≥ －2．  C．x ≥ 2．  D．x ≤ －2．‎ ‎【答案】C ‎30. （ 湖北黄石，10，3分）已知梯形ABCD的四个顶点的坐标分别为A（－1，0），B（5，0），C（2，2），D（0，2），直线y=kx+2将梯形分成面积相等的两部分，则k的值为 A. － B. － C. － D. －‎ ‎【答案】A ‎31. （ 湖南衡阳，6，3分）函数中自变量x的取值范围是（ ）‎ A．≥－3 B．≥－3且 C． D．且 ‎【答案】B ‎32. (20011江苏镇江,5,2分)若在实数范围内有意义,则x的取值范围是( )‎ A.x≥2 B.x≤‎2 C.x＞2 D.x＜2‎ 答案【A 】‎ ‎33. （ 贵州安顺，7，3分）函数中自变量x的取值范围是（ ）‎ ‎ A．x≥0 B．x <0且x≠l C．x<0 D．x≥0且x≠l ‎【答案】D ‎34. （ 河北，5，2分）一次函数y=6x+1的图象不经过（ ）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【答案】D 二、填空题 ‎1. （ 广东东莞，7，4分）使在实数范围内有意义的x的取值范围是 ．‎ ‎【答案】‎ ‎2. （ 山东威海，18，3分）如图，直线轴于点，直线轴于点，直线轴于点，…直线轴于点.函数的图象与直线，，，…分别交于点，，，…；函数的图象与直线，，，…分别交于点，，，….如果的面积记作,四边形 的面积记作,四边形的面积记作,…四边形的面积记作,那么 . ‎ ‎【答案】 .5‎ ‎3. （ 浙江义乌，11，4分）一次函数y=2x－1的图象经过点（a，3），则a= ▲ ．‎ ‎【答案】2‎ ‎4. （ 江西，11，3分）函数y=中，自变量x的取值范围是 .‎ ‎【答案】x≤1‎ ‎5. （ 江西，14，3分）将完全相同的平行四边形和完全相同的菱形镶嵌成如图所示的图案。设菱形中较小角为x度，平行四边形中较大角为y度，则y与x的关系式是 。‎ ‎【答案】y=90+x ‎6. （ 福建泉州，8，4分）在函数中, 自变量的取值范围是 .‎ ‎【答案】‎ ‎7. （ 湖南常德，3，3分）函数中自变量的取值范围是_______________.‎ ‎【答案】‎ ‎8. （ 湖南邵阳，12，3分）函数中，自变量x的取值范围是______。‎ ‎【答案】x≥1.提示：x-1≥0.‎ ‎10．（ 江苏苏州，14,3分）函数y=的自变量x的取值范围是___________________.‎ ‎【答案】x>1‎ ‎11. （ 江苏宿迁,10,3分）函数中自变量x的取值范围是 ▲ ．‎ ‎【答案】x≠2 ‎ ‎12. （ 江苏泰州，17，3分）“一根弹簧原长‎10cm,在弹性限度内最多可挂质量为‎5kg的物体，挂上物体后弹簧伸长的长度与所挂物体的质量成正比， ，则弹簧的总长度y（cm）与所挂物体质量x(kg)之间的函数关系式是y=10+0.5x (0≤x≤5).”‎ 王刚同学在阅读上面材料时就发现部分内容被墨迹污染，被污染部分是确定函数关系式的一个条件，你认为该条件可以是： （只需写出一个）．‎ ‎【答案】悬挂‎2kg物体弹簧总长度为‎11cm. (答案不唯一)‎ ‎13. （ 广东汕头，7，4分）使在实数范围内有意义的x的取值范围是 ．‎ ‎【答案】‎ ‎14. （ 四川广安，13，3分）函数中自变量的取值范围是____‎ ‎【答案】≤2‎ ‎15. （ 四川广安，17，3分）写出一个具体的随的增大而减小的一次函数解析式____‎ ‎【答案】答案不唯一，如：y=－x+1‎ ‎16. （ 四川广安，20，3分）如图4所示，直线OP经过点P(4, )，过x轴上的点l、3、5、7、9、11……分别作x轴的垂线，与直线OP相交得到一组梯形，其阴影部分梯形的面积从左至右依次记为S1、S2、S3……Sn则Sn关于n的函数关系式是____‎ ‎0‎ ‎1‎ ‎3‎ ‎5‎ ‎7‎ ‎9‎ ‎11‎ S1‎ S2‎ S3‎ 图4‎ x y p ‎【答案】(8n－4) ‎ ‎17. （ 重庆江津， 14，4分）函数中x的取值范围是___________.‎ ‎【答案】x＞2·‎ ‎18. （ 江西南昌，11，3分）函数y=中，自变量x的取值范围是 .‎ ‎【答案】x≤1‎ ‎19. （ 山东济宁，11，3分）在函数中, 自变量的取值范围是 .‎ ‎【答案】‎ ‎20．（ 四川成都，21,4分）在平面直角坐标系中，点P(2，)在正比例函数的图象上，则点Q()位于第______象限．‎ ‎【答案】四．‎ ‎21. （ 广东省，7，4分）使在实数范围内有意义的x的取值范围是 ．‎ ‎【答案】‎ ‎22. （ 湖南怀化，12，3分）一次函数y=-2x+3中，y的值随x值增大而___________.(填“增大”或“减小”)‎ ‎【答案】减小 ‎23. （ 江苏南通，13，3分）函数y＝中，自变量x的取值范围是 ▲ .‎ ‎【答案】x≠1.‎ ‎24. （ 上海，10，4分）函数的定义域是_____________．‎ ‎【答案】x≤3‎ ‎25. （ 上海，12，4分）一次函数y＝3x－2的函数值y随自变量x值的增大而_____________（填“增大”或“减小”）．‎ ‎【答案】增大 ‎26. （ 江苏无锡，13，2分）函数y = 中自变量x的取值范围是________________．‎ ‎【答案】x ≥ 4‎ ‎27. （ 湖南衡阳，15，3分）如图，一次函数的图象与轴的交点坐标为（2，0），则下列说法：①随的增大而减小；②>0；③关于的方程的解为．其中说法正确的有 （把你认为说法正确的序号都填上）．‎ ‎【答案】 ①②③‎ ‎28. （ 湖南邵阳，12，3分）函数中，自变量x的取值范围是______。‎ ‎【答案】x≥1.‎ ‎29. （ 贵州贵阳，12，4分）一次函数y=2x-3的图象不经过第______象限．‎ ‎ 【答案】二 ‎30. (20011江苏镇江,16,2分)已知关于x的一次函数y=kx+4k-2(k≠0).若其图象经过原点,则k=_____;若y随x的增大而减小,则k的取值范围是________.‎ 答案：，k<0‎ ‎31. （ 广东湛江18,4分）函数中自变量的取值范围是 ．‎ ‎【答案】‎ ‎32. （2010湖北孝感，13，3分）函数y=的自变量x的取值范围是 .‎ ‎【答案】x≥2‎ ‎33. （ 湖南湘潭市，12，3分）函数中，自变量的取值范围是_________.‎ ‎【答案】x≠1‎ ‎34.‎ 三、解答题 ‎1. (（ 浙江杭州，17，6）点A，B，C，D的坐标如图，求直线AB与直线CD的交点坐标．‎ ‎【答案】求直线AB和CD的解析式分别为：，解方程组得：，则直线AB与直线CD的交点坐标为．‎ ‎2. ( 浙江湖州，19，6) 已知：一次函数的图象经过M(0，2)，(1，3)两点．‎ ‎ (l) 求k、b的值；‎ ‎ (2) 若一次函数的图象与x轴的交点为A(a，0)，求a的值．‎ ‎【答案】(1)由题意得，解得，∴k，b的值分别是1和2.‎ ‎(2)由(1)得，∴当y＝0时，x＝－2，即a＝－2.‎ ‎3. （ 浙江省，23，12分）设直线l1:y1=k1x+b1与l2:y2=k2x+b2，若l1⊥l2，垂足为H，则称直线l1与l2是点H的直角线．‎ ‎(1) 已知直线①；②；③；④和点C（0,3）．则直线 和 是点C的直角线（填序号即可）；‎ ‎(2) 如图，在平面直角坐标系中，直角梯形OABC的顶点A（3,0）、B（2,7）、C（0,7），P为线段OC上一点，设过B、P两点的直线为l1，过A、P两点的直线为l2，若l1与 l2是点P的直角线，求直线l1与 l2的解析式．‎ ‎【答案】（1）画图象可知，直线①与直线③是点C的直角线；（点C的坐标似乎有问题）‎ ‎ （2）设P坐标为(0，m)，则PB⊥PB于点P。因此，AB2=(3-2)2+72=50, ‎ ‎ 又 ∵ PA2=PO2+OA2=m2+32，PB2=PC2+BC2=(7-m)2+22 ,‎ ‎∴AB2=PA2+PB2=m2+32+(7-m)2+22=50‎ ‎ 解得：m1=1，m2=6.‎ ‎ 当m=1时，l1为：y1=， l2为：y2=；‎ ‎ 当m=6时，l1为：y1=, l2为：y2=；‎ ‎4. （ 浙江温州，24，14分）如图，在平面直角坐标系中，O是坐标原点，点A的坐标为(－4，0)，点B的坐标为(0，b)(b>0)． P是直线AB上的一个动点，作PC⊥x轴，垂足为C．记点P关于y轴的对称点为P'（点P'不在y轴上），连结PP'，P'A，P'C．设点P的横坐标为a．‎ ‎(1)当b＝3时，‎ ‎ ①求直线AB的解析式；‎ ‎ ②若点P'的坐标是(-1，m)，求m的值；‎ ‎(2)若点P在第一象限，记直线AB与P'C的交点为D． 当P'D：DC=1：3时，求a的值；‎ ‎(3)是否同时存在a，b，使△P'CA为等腰直角三角形？若存在，请求出所有满足要求的a，b的值；若不存在，请说明理由．‎ ‎【答案】解：(1)①设直线AB的解析式为y=kx+3，‎ 把x＝－4，y＝0代人上式，得－4k+3＝0，‎ ‎∴，‎ ‎∴‎ ‎②由已知得点P的坐标是(1，m)，‎ ‎∴，∴.‎ ‎(2) ∵PP'∥AC，‎ ‎∴△PP'D∽△ACB，‎ ‎∴，‎ ‎∴.‎ ‎(3)以下分三种情况讨论．‎ ‎①当点P在第一象限时，‎ i)若∠AP'C= 90°，P'A= P'C（如图1），过点P'作P'H⊥x轴于点'H，∴PP'=CH=AH=P'H =AC，‎ ‎∴，∴．‎ ‎∵P'H＝PC=AC，△ACP∽△AOB，‎ ‎∴，即，‎ ‎∴．‎ ii)若∠P'AC=90°，P'A= CA(如图2)，则PP'=AC，∴‎2a＝a+4，∴ a＝4．‎ ‎∵P'A＝PC＝AC, △ACP∽△AOB，‎ ‎∴，即，∴．‎ iii)若∠P'CA =90°，则点P'，P都在第一象限，这与条件矛盾，‎ ‎∴△P'CA不可能是以C为直角顶点的等腰直角三角形．‎ ‎②当点P在第二象限时，∠P'CA为钝角（如图3），此时△P'CA不可能是等腰直角三角形．‎ ‎③当点P在第三象限时，∠PAC为钝角（如图4）， 此时△P'CA不可能是等腰直角三角形，∴所有满足条件的a，b的值为.‎ ‎5. ( 浙江绍兴，21，10分)在平面直角坐标系中，过一点分别作坐标轴的垂线，若与坐标轴围成矩形的周长与面积相等，则这个点叫做和谐点.例如，图中过点分别作轴，轴的垂线，与坐标轴围成矩形的周长与面积相等，则点是和谐点.‎ 第21题图 ‎（1）判断点是否为和谐点，并说明理由；‎ ‎（2）若和谐点在直线上，求点的值. ‎ ‎【答案】（1）‎ 点不是和谐点，点是和谐点.‎ ‎（2）由题意得，‎ 当时，‎ ‎，点在直线上，代入得；‎ 当时，‎ ‎，点在直线上，代入得.‎ ‎6. （ 江苏盐城，28，12分）如图，已知一次函数y = - x +7与正比例函数y = x的图象交于点A，且与x轴交于点B.‎ ‎（1）求点A和点B的坐标；‎ ‎（2）过点A作AC⊥y轴于点C，过点B作直线l∥y轴．动点P从原点O出发，以每秒1个单位长的速度，沿O—C—A的路线向点A运动；同时直线l从点B出发，以相同速度沿x轴向左平移，在平移过程中，直线l交x轴于点R，交线段BA或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P运动的时间为t秒.‎ ‎①当t为何值时，以A、P、R为顶点的三角形的面积为8？‎ ‎②是否存在以A、P、Q为顶点的三角形是等腰三角形？若存在，求t的值；若不存在，请说明理由．‎ ‎（备用图）‎ ‎【答案】（1）根据题意，得，解得 ，∴A(3，4) . ‎ 令y=-x+7=0，得x=7．∴B（7，0）. ‎ ‎（2）①当P在OC上运动时，0≤t＜4.‎ 由S△APR=S梯形COBA-S△ACP-S△POR-S△ARB=8，得 (3+7)×4-×3×(4-t)- t(7-t)- t×4=8‎ 整理,得t2-8t+12=0, 解之得t1=2,t2=6（舍） ‎ 当P在CA上运动，4≤t＜7. ‎ 由S△APR= ×(7-t) ×4=8，得t=3（舍） ‎ ‎∴当t=2时，以A、P、R为顶点的三角形的面积为8.‎ ‎ ②当P在OC上运动时，0≤t＜4.‎ ‎∴AP=，AQ=t，PQ=7-t 当AP =AQ时， （4-t）2+32=2(4-t)2,‎ 整理得，t2-8t+7=0. ∴t=1, t=7(舍) ‎ 当AP=PQ时，（4-t）2+32=(7-t)2,‎ 整理得，6t=24. ∴t=4(舍去) ‎ 当AQ=PQ时，2（4-t）2=(7-t)2‎ 整理得，t2-2t-17=0 ∴t=1±3 (舍) ‎ 当P在CA上运动时，4≤t＜7. 过A作AD⊥OB于D,则AD=BD=4.‎ 设直线l交AC于E，则QE⊥AC，AE=RD=t-4，AP=7-t.‎ 由cos∠OAC= = ，得AQ = (t-4)．‎ 当AP=AQ时，7-t = (t-4)，解得t = . ‎ 当AQ=PQ时，AE＝PE，即AE= AP 得t-4= (7-t)，解得t =5. ‎ 当AP=PQ时，过P作PF⊥AQ于F AF= AQ = ×(t-4). ‎ 在Rt△APF中，由cos∠PAF＝ ＝ ，得AF＝ AP 即 ×(t-4)= ×(7-t)，解得t= .‎ ‎∴综上所述，t=1或 或5或 时，△APQ是等腰三角形.‎ ‎7‎ 一次函数（正比例函数）的图象与性质B 一、选择题 ‎1. （ 广西桂林，8，3分）直线y=kx-1一定经过点（ ）．‎ ‎ A．（1，0） B．（1，k） C．（0，k） D．（0，-1）‎ ‎ 【答案】D ‎2. （ 贵州毕节，8，3分）函数中自变量的取值范围是( )‎ ‎ A．≥-2 B．≥-2且≠‎1 C．≠1 D．≥-2或≠1‎ ‎【答案】B ‎3. （ 湖北十堰，2，3分）函数中自变量x的取值范围是（ ）‎ A．x≥0 B.x≥‎4 C.x≤4 D.x＞4‎ ‎【答案】B ‎4. （ 湖北随州，14，3分）如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A、B的坐标分别为（1，0）、（4，0），将△ABC沿x轴向右平移，当点C落在直线y=2x－6上时，线段BC扫过的面积为（ ）‎ A．4 B．‎8 ‎ C．16 D．‎ ‎ 第14题图 A B C O y x ‎【答案】C ‎6. ( 江苏常州,5,2分)若在实数范围内有意义,则x的取值范围是( )‎ A.x≥2 B.x≤‎2 C.x＞2 D.x＜2‎ ‎【答案】A ‎7. （ 贵州遵义，7，3分）若一次函数的函数值随的增大而减小，则的取值范围是 A. B. C. D. ‎ ‎【答案】D ‎8. （ 广东清远，9，3分）一次函数的图象大致是（ ）‎ ‎【答案】A ‎9. （ 广西桂林，8，3分）直线一定经过点（ ）．‎ ‎ A．（1，0） B．（1，k） C．（0，k） D．（0，-1）‎ ‎【答案】D ‎10．（ 广西南宁，5，3分）函数y=中，自变量x的取值范围是：‎ ‎ (A)x≠2 (B)x≥2 ( C)x≤2 (D)全体实数 ‎【答案】B ‎11. （ 广西梧州，10，3分）如图4，在平面直角坐标系中，直线y=x－与矩形ABCD的边OC、BC分别交于点E、F，已知OA=3，OC=4，则△CEF的面积是 ‎（A） （B） ‎ ‎（C） （D）‎ y y A B O E F C 图4‎ ‎【答案】B ‎12. （ 湖北鄂州，14，3分）如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A、B的坐标分别为（1，0）、（4，0），将△ABC沿x轴向右平移，当点C落在直线y=2x－6上时，线段BC扫过的面积为（ ）‎ A．4 B．‎8 ‎ C．16 D．‎ ‎ 第14题图 A B C O y x ‎【答案】C ‎13. （ 黑龙江绥化，14，3分）向大容量为‎60升的热水器内注水，每分钟注水‎10升，注水2分钟后停止注水1分钟，然后继续注水，直至注满.则能反映注水量与注水时间函数关系的图象是（ ）‎ ‎【答案】D ‎14. （ 内蒙古包头，4，3分）函数中自变量x的取值范围是（ ）‎ A．x≥2且x≠－3 B．x≥‎2 ‎ C．x＞2 D．x≥2且x≠0‎ ‎【答案】B ‎15. （ 湖北潜江天门仙桃江汉油田，9，3分）如图，已知直线l：y=x，过点A（0，1）作y轴的垂线 交直线l于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直 线l的垂线交y轴于点A2；…；按此作法继续下去，则点A4的坐标为（ ）‎ A．（0，64） B．（0，128） C．（0，256） D．（0，512）‎ ‎【答案】C ‎16. （ 湖北省随州市，6，4分）如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A、B的坐标分别为（1，0）、（4，0），将△ABC沿x轴向右平移，当点C落在直线y=2x-6上时，线段BC扫过的面积为（ ）‎ A．4 B．‎8 ‎ C．16 D．8‎ 第6题图 ‎【答案】C ‎17. （ 江西b卷，5,3分）已知一次函数y=－x+b的图象经过第一、二、四象限，则b的值可以是( ).‎ A .－2 B.－‎1 C. 0 D. 2‎ ‎【答案】D ‎18. （ 山东枣庄，10，3分）如图所示，函数和的图象相交于（－1，1），（2，2）两点．当时，x的取值范围是（ ）‎ ‎（－1，1）‎ ‎（2，2）‎ x y O A．x＜－1 B．—1＜x＜‎2 ‎‎ C．x＞2 　　D． x＜－1或x＞2 ‎ ‎【答案】D ‎19. （201１四川广元，9，3分）在函数中自变量x 的取值范围在数轴上表示为（ C ）‎ ‎ ‎ A． B． ‎ ‎ ‎ C． D． ‎ ‎【答案】C ‎20．（ 四川眉山，3，3分）函数y=中自变量x的取值范围是 ‎ A．x≠一2 B．x≠‎2 C. x<2 D．x>2‎ ‎【答案】B ‎21. （ 广西来宾，3，3分）使函数有意义的取值范围是（ ）‎ A. B. C. 1且x≠0 D. 且x≠0‎ ‎【答案】 A ‎22. （ •泸州3，2分）已知函数，则自变量x的取值范围是（　　）‎ ‎ A、x≠2 B、x＞2‎ ‎ C、 D、且x≠2‎ ‎【答案】D．‎ ‎23. （ 四川自贡，2，3分）函数中，自量变的取值范围是 （ ）‎ A. ≥1 B. >‎1 C. ≥1且≠2 D. >1且≠2 ‎ ‎【答案】C ‎24. （ 四川自贡，8，3分）已知直线经过点A（1,0）且与直线垂直，则直线的解析式为 （ ）‎ A. B. C. D. ‎ ‎【答案】A ‎25. （2010乌鲁木齐，5，4分)将直线向右平移1个单位后所得图象对应的函数解析式为 ‎ A. B. ‎ C. D. ‎ ‎【答案】B ‎ ‎26. （ 张家界，8，3分）关于x的一次函数y=kx+k2+1的图像可能是（ ）‎y y y y A B C D x O x O x O x O ‎ ‎ ‎【答案】C ‎27. ( 湖南郴州市，2，3分)函数自变量的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】A 二、填空题 ‎1. （ 广东河源，7,4分）函数 的自变量的取值范围是．‎ ‎【答案】x≠1‎ ‎2. （ 广东湛江，18,4分）函数中自变量的取值范围是 ．‎ ‎【答案】‎ ‎3. （ 贵州毕节，16，5分）已知一次函数的图象如图所示，‎ 则不等式的解集是 。‎ ‎3‎ ‎0‎ ‎1.5‎ x y ‎(第16题)‎ ‎【答案】x＞1.5‎ ‎4. （ 黑龙江省哈尔滨市，12，3分）在函数中，自变量x的取值范围是 _。‎ ‎【答案】‎ ‎5. ( 江苏常州,16,2分)已知关于x的一次函数y=kx+4k-2(k≠0).若其图象经过原点,则k=_____;若y随x的增大而减小,则k的取值范围是________.‎ ‎【答案】; k<0‎ ‎6. （ 陕西，15,3分）若一次函数的图像经过 一、二、四象限，则m的取值范围是 ．‎ ‎【答案】‎ ‎7. （ 天津，13,3分）已知一次函数的图象经过点（0,1），且满足随增大而增大，则该一次函数的解析式可以为_________________（写出一个即可）.‎ 答案：（答案不唯一，可以是形如，的一次函数）‎ ‎8. （ 湖南娄底，14,4分）一次函数y= -3 x + 2的图象不经过第 象限.‎ ‎【答案】三 ‎9. （ 内蒙古呼和浩特市，11,3分）函数中，自变量x的取值范围_________________________.‎ ‎【答案】‎ ‎10．（ 内蒙古呼和浩特市，12,3分）已知关于x的一次函数的图象如图所示，则可化简 为_________________.‎ ‎【答案】n ‎11. （ 福建莆田，16，4分）已知函数，其中f(a)表示x=a时对应的函数值，‎ 如，，，‎ 则_ ▲ ．‎ ‎ 【答案】5151‎ ‎12. （ 黑龙江省哈尔滨市，12，3分）在函数中，自变量x的取值范围是 _。‎ ‎【答案】1.7×105‎ ‎13. （ 黑龙江绥化，2，3分）函数中，自变量的取值范围是 .‎ ‎【答案】且 ‎14. （ 吉林长春，13,3分）如图，一次函数的图象经过点Ａ．当时，的取值范围是＿＿＿＿＿＿＿＿．‎ ‎【答案】‎ ‎15. （ 辽宁沈阳，13，4分）如果一次函数y=4x+b的图像经过第一、三、四象限，那么b的取值范围是_______________。‎ ‎【答案】b＜0‎ ‎16. （ 内蒙古赤峰，11，3分）已知点A（－5，a），B(4，b)在直线y=-3x+2上，则a______b。（填“＞”、“＜”或“=”号）‎ ‎【答案】＞‎ ‎18. （ 年青海，5,2分）函数y=中，自变量x的取值范围是 。‎ ‎【答案】x≥－3且x≠1‎ ‎19. （ 湖南岳阳，9,3分）函数中自变量x的取值范围是 ．‎ ‎【答案】‎ ‎20．（ 贵州黔南，15,5分）函数y=中，自变量x的取值范围是 ‎ ‎【答案】x＜2‎ ‎21. （ 辽宁本溪，9，3分）函数y＝中自变量x的取值范围是 ．‎ ‎【答案】x≠4‎ ‎22. （ 青海西宁，13，2分）如表1给出了直线l1上部分点（x，y）的坐标值，表2给出了直线l2上部分（x，y）的坐标值．那么直线l1和直线l2交点坐标为______．‎ ‎ ‎表1 表2‎ ‎【答案】（2，﹣1）‎ ‎23. （ 青海西宁，20，2分）如图11，直线y=kx+b经过A（﹣1，1）和B（，0）两点，则不等式0＜kx+b＜﹣x的解集为______．‎ ‎ ‎ ‎【答案】﹣＜x＜﹣1‎ ‎24. （ 黑龙江黑河，2，3分）函数y=中，自变量x的取值范围是 . ‎ ‎【答案】x≥－2且x≠3‎ ‎25.‎ ‎26. （ 黑龙江黑河，14，3分）向最大容量为‎60升的热水器内注水，每分钟注水‎10升，注水2分钟后停止注水1分钟，然后继续注水，直至注满.则能反映注水量与注水时间函数关系的图象是 ( )‎ A B C D ‎【答案】D 三、解答题 ‎1. ( 江苏常州,24,7分)如图,在△ABO中,已知点A(,3),B(-1,-1),O(0,0),正比例y=-x的图象是直线l,直线AC∥x轴交直线l于点C.‎ ‎(1)C点坐标为_____;‎ ‎(2)以点O为旋转中心,将△ABO顺时针旋转角a(0°‎36升，‎ ‎∴油箱中的油够用．‎ ‎7. （ 年铜仁地区，19（2），4分）已知一次函数y=kx+b的图像经过两点A(1,1)，B(2,-1)，求这个函数的解析式．‎ ‎【答案】根据题意得 ………………………………..…… 2分 ‎ ‎ 解得 …………………………………………….…… 4分 ‎ 所以函数的解析式是y=-2x+3………………………………….……… 5分 ‎8. （ 云南玉溪，23，12分）如图，在Rt△OAB中，∠ABO=30°，OB=，边AB的垂直平分线CD分别与AB、x轴、x轴交于点C、G、D.‎ ‎（1）求点G的坐标； ‎ ‎（2）求直线CD的解析式；‎ ‎（3）在直线CD上和平面内是否分别存在点Q、P，使得以O、D、P、Q为顶点的四边形是菱形？若存在，求出点Q的坐标；若不存在，请说明理由. ‎ ‎【答案】(1) ∵DC是AB的垂直平分线，OA垂直AB，‎ ‎∴G点为OB的中点，∵OB=,∴G ‎(2)过点C作CH⊥x轴于点H 在Rt△ABO中，∠ABO=30°，OB=，‎ ‎∴cos30°=，即AB=×=4，‎ 又∵CD垂直平分AB，∴BC=2，在Rt△CBH中，CH=BC=1，BH=,‎ ‎∴OH=-=，∴C（，-1），∵∠DGO=60°，∴OG=OB=，‎ ‎∴OD=4，∴D（0,4）.设直线CD的解析式为x=kx+B，则 ‎，∴，∴.‎ ‎（3）存在点P、Q，使得以O、D、P、Q为顶点的四边形是菱形.‎ ‎①如图，当OD=DQ=QP=OP=4时四边形DOPQ是菱形.‎ 设QP交x轴于点E，在Rt△OEP中，OP=4，∠OPE=30°，‎ ‎∴OE=2，PE=2,∴Q（2,4-2）.‎ ‎②如图当OD=DQ=QP=OP=4时，四边形DOPQ是菱形.‎ 延长QP交x轴于点F，在Rt△POF中，∵∠FPO=30°，OP=4,‎ ‎∴OF=2，PF=2,∴QF=4+2,∴Q（-2，4+2）‎ ‎③如图，当OD=DQ=QP=OP=时，四边形DOPQ是菱形.‎ 过点Q作MQ⊥x轴于点M，‎ 在Rt△DQM中，∵∠MDQ=30°，‎ ‎∴MQ=DQ=，∴Q（，2）‎ ‎④如图，如图当OD=DQ=QP=OP=4时，四边形DOPQ是菱形.‎ 设PQ交x轴于点N，此时∠OQD=∠ODQ=30°，∴∠GOQ=30°，‎ 在Rt△ONQ中,NQ=OQ=2，∴ON=,∴Q(,-2).‎ 综上所述，满足条件的点Q共有四点：‎ ‎（2,4-2）、（-2，4+2）、（，2）、(,-2)‎ ‎9. （ 湖南岳阳，20,6分）如图，一次函数图象与x轴相交于点B，与反比例函数图象相交A（1，-6），△AOB的面积为6．求一次函数和反比例函数的解析式．‎ A Bx O y x ‎（第20题图）‎ ‎【答案】点B坐标为（-2，0）。把点A（1，-6），B（-2，0）分别代入反比例函数中，得，，所以。把点A（1，-6），B（-2，0）分别代入一次函数y=kx+b，得，解得，所以y=-2x-4。‎ ‎10．( 湖南郴州市，20，6分)求与直线平行，并且经过点P(1，2)的一次函数解析式．‎ ‎【解】设一次函数解析式为，‎ 因为图象与直线平行，‎ 所以，‎ 图象过点P(1，2)，所以，所以，‎ 所以一次函数解析式.‎ ‎11. （ 福建漳州，25，13分）如图，直线与轴、轴分别交于A、B两点，将△OAB绕点O逆时针方向旋转90°后得到△OCD。‎ ‎（1）填空：点C的坐标是（_______，_______）；‎ ‎ 点D的坐标是（_______，_______）。‎ ‎（2）设直线CD与AB交于点M，求线段BM的长；‎ ‎（3）在y轴上是否存在点P，使得△BMP是等腰三角形？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由。‎ ‎【解】（1）点C 的坐标为（0，1），点D 的坐标为（-2，0）‎ ‎(2)方法一.由（1）可知,BC=1又,‎ 所以△BMC∽△DOC. ‎ 方法二：设直线CD的解析式为，可得：过CD的直线解析式为 所以，所以点M的坐标为 过点M作ME⊥y轴于点E，则.‎ ‎ (3)存在；分两种情况讨论 ‎①以BM为腰时 ‎，又点P在y轴上，且BP=BM此时满足条件的点P 有两个它们是，‎ 过点M作ME⊥y轴于点E。‎ 则△BME∽△BCM 又因为BM=MP所以FE=BE=,所以BP=‎ 所以CP=，此时满足条件的点P有一个，它是 ‎②以BM为底时，作BM的垂直平分线，分别交y轴BM于点P,F，由（2）得 ‎∥CM，因为点F 是EM的中点，所以EP=,所以OP=，此时满足条件的点P有一个，它是 综上所述，点P的坐标是